af3fcf5311fcdfea654122e1246bbf1f.ppt
- Количество слайдов: 31

A Unified Framework for Constraint Based Shared Memory Consistency Analysis a presentation in CP+CV’ 04 Yue Yang, Ganesh Gopalakrishnan, Gary Lindstrom, Konrad Slind School of Computing University of Utah Supported in part by SRC Contract 1031. 001 and NSF Grants CCR-0081406, 0219805

Problem Context #1: The design of efficient multiprocessors Efficient Multiprocessors have Efficient Shared Memory Systems . . . because CPUs grow faster than memory systems 2

Efficient Shared-memory Multiprocessor Systems employ • Weak memory models – Controlled ways to postpone global view updates. Advanced consistency protocols, advanced OS libraries, . . . depend on it Problem: How to specify these weak memory models? How to use the specification in practice to support verification activities? 3

Problem Context #2: The design of multithreaded software Language-level weak memory models are being studied . . . because languages with explicit threading cannot be implemented efficiently on a wide variety of platforms Examples: Java C# Open. MP Re-entrant device drivers OS code that runs very fast with minimal locking. . . 4

Characteristics of language-level memory models • Weak memory models – Controlled ways to postpone global view updates – Encompass compiler optimizations that “make sense” Problem: How to specify language-level memory models? How to use the specification in practice to support verification activities? 5

Answer: Constraints seem very attractive! • Constraint-based specification of several architecture-level memory models • The use of these specifications to enable formal comparisons among the models • The use of these specs for post-silicon verification (work in collaboration with Intel) (FOCUS OF THIS TALK) • Analysis of proposals for language-level memory models (Yang’s dissertation) • The use of specs of language-level memory models for – Memory-model sensitive program analysis (preliminary work in Yang’s dissertation) – . . . for certifying compilers that exploit language-level memory models (future work) 6

Publications • Yang, Y. , Gopalakrishnan, G. , Lindstrom, G. , and Slind, K. , “Analyzing the Intel Itanium Memory Ordering Rules using Logic Programming and SAT, ” Charme 2003, LNCS 2860, October 2003. • Yang, Y. , Gopalakrishnan, G. , Lindstrom, G. , and Slind, K. , “Nemos: A framework for axiomatic and executable specifications of memory consistency models, ” IPDPS 2004, Santa Fe, NM, April 2004. • Yang, Y. , Gopalakrishnan, G. , and Lindstrom, G. , “A Constraint Based Approach for Specifying Memory Consistency Models, ” Journal of Logic Programming (submitted to a special issue on constraints) • Gopalakrishnan, G. , Yang, Y. , and Hemanthkumar, S. , “QB or not QB: An efficient verification tool for memory orderings, ” Accepted by CAV’ 04 7

Proof of concept Software • Nemos (Yue Yang) – Defines memory models via Constraint Logic Programs – Constraint-Prolog code available for experimentation • Defect. Finder (Yue Yang) – Constraint-Prolog code that models race and atomicity analysis – works in the small (no loops at present) – underlying shared memory model given as an explicit parameter • • QBF-based Memory Order Checker – – written by the PI in Ocaml Compiles memory order rules written in HOL to QBF Does not scale yet Might provide benchmarks to tune QBF-tools SAT-based Memory Order Checking Tool – – Present version written by the PI in Ocaml Next version expected to be formally derived Replaces Constraint-Prolog version for Itanium One “real” execution given by Intel was successfully run 8

Another effort involving constraints (presented at DCC’ 04): Limited Observability Run-time Verification (with Ching Tsun Chou) 9

The rest of the talk: Post-Si verification of MP Orderings using Constraints 10

Weak memory models allow multiple executions. . . st c, 1 ; st d, 2 CPU One possible execution. . . Another execution. . . ld d; ld c CPU st c, 1 ; st d, 2 ld d, 2; ld c, 0 st c, 1 ; st d, 2 ld d, 2; ld c, 1 Memory Impossible under SC Possible under Itanium Possible under SC and under Itanium 11

Commercial Weak Memory Model Specs are Complex • Intel’s original specification was pretty voluminous • They later issued a formal spec that clarified many things • Yet, their “formal” spec left many things informal • It was purely “on paper” (no machine-readable formal spec) • Our exercise was to take Intel’s semi-formal spec and capture it in HOL • Result: 36 pages of Intel’s formal spec in 3 pages of HOL spec • Can prove “challenge theorems” (future work) 12

Basic idea behind Intel’s Formal Spec (which we follow in our formal spec) Make it look like SC so that people have less trouble understanding! SC(ops) = Exists order. ( require. Strict. Total. Order ops order / require. Program. Order ops order / require. Read. Value ops order Call it “other. Order” legal. Itanium(ops) = Exists order. ( require. Strict. Total. Order ops order / / ops order ops order require. Write. Operation. Order require. It. Program. Order require. Memory. Data. Dependence require. Data. Flow. Dependence require. Coherence require. Atomic. WBRelease require. Sequential. UC require. No. UCBypass / require. Read. Value ops order 13

But, how do we check executions against such specs? SC(ops) = Exists order. ( require. Strict. Total. Order ops order legal. Itanium(ops) = Exists order. ( require. Strict. Total. Order ops order / require. Program. Order ops order / require. Read. Value ops order / / ops order ops order require. Write. Operation. Order require. It. Program. Order require. Memory. Data. Dependence require. Data. Flow. Dependence require. Coherence require. Atomic. WBRelease require. Sequential. UC require. No. UCBypass / require. Read. Value Execution 1 st c, 1 ; ld d, 2; st d, 2 ld c, 0 ops order Execution 2 st c, 1 ; ld d, 2; st d, 2 ld c, 1 e. g. , which execution is legal under which memory model ? 14

Why care about Execution Validation? • In complex systems, FV helps eliminate (most) bugs • Must verify final silicon also (as far as possible) (Note: this is different from “fabrication fault” testing) • FV can help immensely during Post-Silicon Verification !! - This is like “runtime verification” ala. Havelund, Rosu, Lee, . . . 15
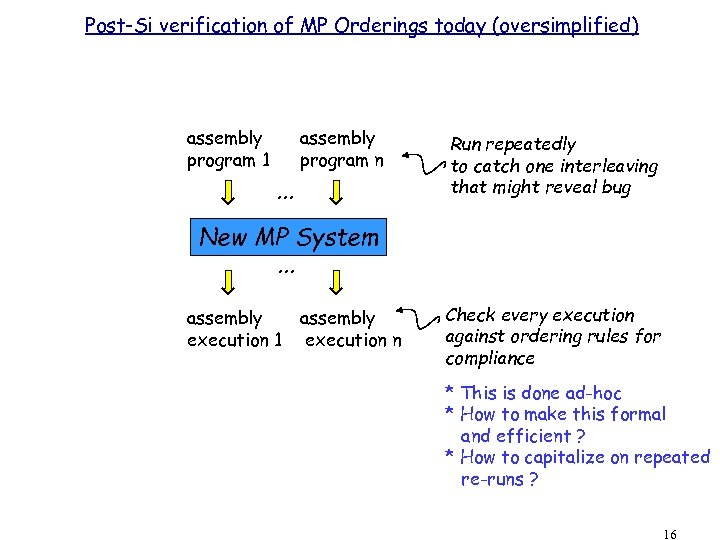
Post-Si verification of MP Orderings today (oversimplified) assembly program 1 assembly program n . . . Run repeatedly to catch one interleaving that might reveal bug New MP System. . . assembly execution 1 assembly execution n Check every execution against ordering rules for compliance * This is done ad-hoc * How to make this formal and efficient ? * How to capitalize on repeated re-runs ? 16

Initial approach tried and abandoned. . . require. Program. Order ops order = Forall i, j : ops ( ordered. By. Acquire i j / ordered. By. Release i j / ordered. By. Fence i j ) ==> order i j ( % Rule (ACQ): ACQ>>I. . . #/ % Rule (REL): Op_j #= St. Rel #/ ( Is. Wr_i #==> (Wr. Type_i #= Local #/ Wr. Type_j #= Local #/ Wr. Type_i #= Remote #/ Wr. Type_j #= Remote #/ Wr. Proc_i #= Wr. Proc_j) ) #==> Oij. . . IMPOSES CONSTRAINT ON MATRIX ENTRY Oij 17

Our new SAT-based execution formal verification method legal. Itanium(ops) = Exists order. ( require. Strict. Total. Order ops order / require. Write. Operation. Order / require. It. Program. Order / require. Memory. Data. Dependence / require. Data. Flow. Dependence / require. Coherence / require. Atomic. WBRelease / require. Sequential. UC / require. No. UCBypass ops order ops order / require. Read. Value Execution st c, 1 ; ld d, 2; st d, 2 ld c, 1 ops order Hand-derivation now. . . to be automated Program capturing memory ordering rules SAT instance Sat Solver Find out which instructions violated what ordering rules. . . Extract Unsat core (currently done using Zcore) UNSAT Explanation (How things may bypass each other. . . ) 18

Have built tool for tuple-generation that addresses many details: (1) Expansion into tuples with variable address allocation P 1: St a, 1; Ld r 1, a <1>; St b, r 1 <1>; P 2: Ld. acq r 2, b <1>; Ld r 3, a <0>; {id=0; proc=0; pc=0; op= St; var=0; data=1; wr. ID=0; wr. Type=Local; wr. Proc=0; reg=-1; use. Reg=false}; Tuple 1 {id=1; proc=0; pc=0; op= St; var=0; data=1; wr. ID=0; wr. Type=Remote; wr. Proc=0; reg=-1; use. Reg=false}; {id=2; proc=0; pc=0; op= St; var=0; data=1; wr. ID=0; wr. Type=Remote; wr. Proc=1; reg=-1; use. Reg=false}; {id=3; proc=0; pc=1; op= Ld; var=0; data=1; wr. ID=-1; wr. Type=Dont. Care; wr. Proc=-1; reg=0; use. Reg=true}; {id=4; proc=0; pc=2; op= St; var=1; data=1; wr. ID=4; wr. Type=Local; wr. Proc=0; reg=0; use. Reg=true}; . . . {id=5; proc=0; pc=2; op= St; var=1; data=1; wr. ID=4; wr. Type=Remote; wr. Proc=0; reg=0; use. Reg=true}; {id=6; proc=0; pc=2; op= St; var=1; data=1; wr. ID=4; wr. Type=Remote; wr. Proc=1; reg=0; use. Reg=true}; {id=7; proc=1; pc=0; op= Ld. Acq; var=1; data=1; wr. ID=-1; wr. Type=Dont. Care; wr. Proc=-1; reg=1; use. Reg=true}; {id=8; proc=1; pc=1; op= Ld; var=0; data=0; wr. ID=-1; wr. Type=Dont. Care; wr. Proc=-1; reg=2; use. Reg=true} Tuple 8 19
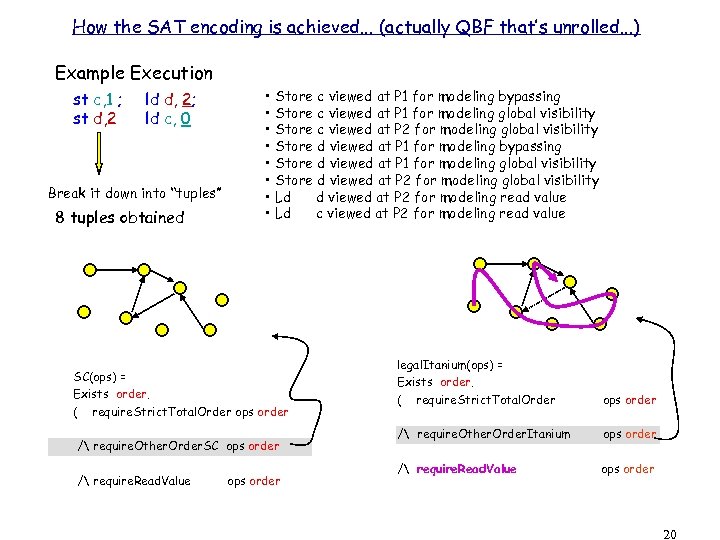
How the SAT encoding is achieved. . . (actually QBF that’s unrolled. . . ) Example Execution st c, 1 ; st d, 2 ld d, 2; ld c, 0 Break it down into “tuples” 8 tuples obtained • Store c viewed at P 1 for modeling bypassing • Store c viewed at P 1 for modeling global visibility • Store c viewed at P 2 for modeling global visibility • Store d viewed at P 1 for modeling bypassing • Store d viewed at P 1 for modeling global visibility • Store d viewed at P 2 for modeling global visibility • Ld d viewed at P 2 for modeling read value • Ld c viewed at P 2 for modeling read value SC(ops) = Exists order. ( require. Strict. Total. Order ops order / require. Other. Order. SC ops order / require. Read. Value ops order legal. Itanium(ops) = Exists order. ( require. Strict. Total. Order ops order / require. Other. Order. Itanium ops order / require. Read. Value ops order 20

Constraint Encoding Approach #1 n logn approach (“small domain” encoding) • Attach a word w_t of 2 bits to each tuple t • Tuple i before Tuple j --> Assert wi < wj • Strict. Total. Order --> Assert that the wt words are distinct • Smaller # of Boolean Vars • Much Harder SAT instances (abandoned for now) Illustration on 4 tuples x 00 x 01 x 20 x 21 x 10 x 11 x 30 x 31 require. Strict. Total. Order ops order require. Other. Order require. Read. Value ops order For all i, j: xi 1, xi 0 != xj 1, xj 0 A system of constraints with primitive constraint xi 1, xi 0 < xj 1, xj 0 21
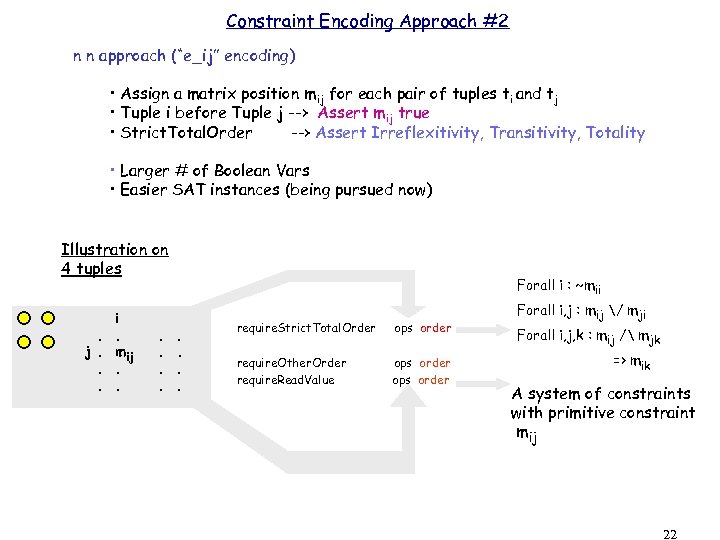
Constraint Encoding Approach #2 n n approach (“e_ij” encoding) • Assign a matrix position mij for each pair of tuples ti and tj • Tuple i before Tuple j --> Assert mij true • Strict. Total. Order --> Assert Irreflexitivity, Transitivity, Totality • Larger # of Boolean Vars • Easier SAT instances (being pursued now) Illustration on 4 tuples . j. . . i. mij. . . Forall i : ~mii. . require. Strict. Total. Order ops order require. Other. Order require. Read. Value ops order Forall i, j : mij / mji Forall i, j, k : mij / mjk => mik A system of constraints with primitive constraint mij 22

Transformation of HOL specs to generate constraints i k Initial Spec j atomic. WBRelease(ops, order) = forall (i in ops). (j in ops). (k in ops). (i. op = St. Rel) / (i. wr. Type = Remote) / (attr_of i. var = WB) / (i. wr. ID = k. wr. ID) / order(i, j) / order(j, k) ==> (j. wr. ID = i. wr. ID) Applying Contrapositive atomic. WBRelease(ops, order) = forall (i in ops). (j in ops). (k in ops). (i. op = St. Rel) / (i. wr. Type = Remote) / (attr_of i. var = WB) / (i. wr. ID = k. wr. ID) / ~(j. wr. ID = i. wr. ID) ==> ~(order(i, j) / order(j, k)) After Reducing quantifier Scopes atomic. WBRelease(ops, order) = forall (i in ops). (i. op = St. Rel) / (i. wr. Type = Remote) / (attr_of i. var = WB) ==> forall (k in ops). (i. wr. ID = k. wr. ID) ==> forall (j in ops). ~(j. wr. ID = i. wr. ID) ==> ~(order(i, j) / order(j, k)) 23

Functional (Ocaml) Program Derivation from HOL Specs: Transformed Spec atomic. WBRelease(ops, order) = forall (i in ops). (i. op = St. Rel) / (i. wr. Type = Remote) / (attr_of i. var = WB) ==> forall (k in ops). (i. wr. ID = k. wr. ID) ==> forall (j in ops). ~(j. wr. ID = i. wr. ID) ==> ~(order(i, j) / order(j, k)) Functional Program that generates the constraints (will be automated) atomic. WBRelease(ops) = forall(i, ops, wb(i)) wb(i) = if ~((attr_of i. var=WB) & (i. op=St. Rel) & (i. wr. Type=Remote) then true else forall(k, ops, wb 1(i, k)) wb 1(i, k) = if ~(i. wr. ID=k. wr. ID) else forall(j, ops, wb 2(i, k, j)) then true wb 2(i, k, j) = if (j. wr. ID=i. wr. ID) else ~(order(i, j) & order(j, k)) then true forall(i, S, e(i)) = for all i in S : e(i) (* foldr( map (fn i -> e(i)) (S) (&), true) *) 24

Main Result: Formally hand-derived code worked first time on all 17 of Intel’s litmus tests! Previous ad-hoc Prolog code had to be massively debugged Formal derivation ensures that HOL axioms are preserved in code that generates SAT instances (very error-prone coding otherwise) 25
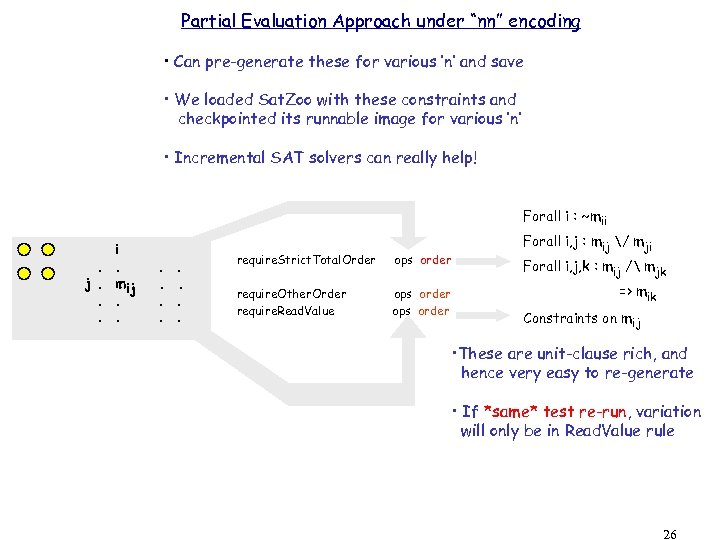
Partial Evaluation Approach under “nn” encoding • Can pre-generate these for various ‘n’ and save • We loaded Sat. Zoo with these constraints and checkpointed its runnable image for various ‘n’ • Incremental SAT solvers can really help! Forall i : ~mii. j. . . i. mij. . require. Strict. Total. Order ops order require. Other. Order require. Read. Value ops order Forall i, j : mij / mji Forall i, j, k : mij / mjk => mik Constraints on mij • These are unit-clause rich, and hence very easy to re-generate • If *same* test re-run, variation will only be in Read. Value rule 26

Recent Practical Test Run Suggests Bounded Cycle Checking: Forall i : ~mii . j. . . i. mij. . require. Strict. Total. Order ops order require. Other. Order require. Read. Value ops order Forall i, j : mij / mji Forall i, j, k IN BOUNDED RANGES mij / mjk => mik • Process Other. Order First • Incremental Constraint Gen for Read. Value 27

Latest results • Intel-provided test of 124 instructions • Generated about 246 tuples • Will not finish unless we rework transitivity • Generated SAT instance with transitivity suppressed, and it found the violation (fluke) • 115, 637 variables and 164, 848 clauses • Zcore found UNSAT core of 9 clauses !! • Better methods to handle transitivity to be implemented – Upper triangular matrix alone will do – Lazy Transitivity introduction • Generate constraints w/o transitivity • If UNSAT, done • Else find SAT instance, force transitivity, re-check. . . 28

Gist of results 1. n n method is superior despite using more bits 2. Checkpointing method does pay-off upto 64 tuples. . . 3. Present approach won’t allow more than 512 tuples #clauses = 7 * n^3 +. . . where n is the number of tuples #variables = 2 * n^3 +. . . 4. Several solutions to be considered: • Generate upper-triangular alone • Generate w/o transitivity ; lazily introduce it • Look for natural limits due to CPU resources • Exploit barriers in code • Heuristically enumerate cycles of increasing sizes 29
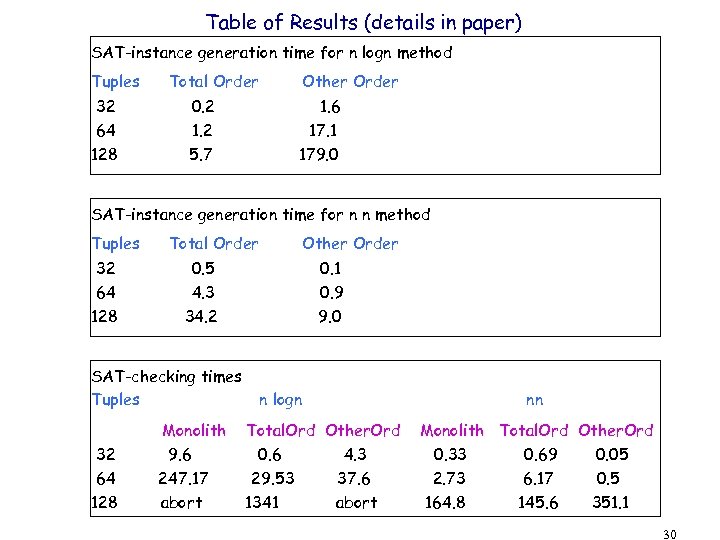
Table of Results (details in paper) SAT-instance generation time for n logn method Tuples Total Order Other Order 32 64 0. 2 1. 6 17. 1 128 5. 7 179. 0 SAT-instance generation time for n n method Tuples 32 64 128 Total Order 0. 5 4. 3 34. 2 SAT-checking times Tuples 32 64 128 Other Order Monolith 9. 6 247. 17 abort 0. 1 0. 9 9. 0 n logn Total. Ord Other. Ord 0. 6 4. 3 29. 53 37. 6 1341 abort nn Monolith Total. Ord Other. Ord 0. 33 0. 69 0. 05 2. 73 6. 17 0. 5 164. 8 145. 6 351. 1 30

Concluding Remarks • Constraint-based shared memory consistency specification is advantageous in many ways • Preliminary work was done using Constraint-Prolog • Recent work being done using SAT • Need to focus on methods that can combine static constraint solving (in program code) and explicit constraint solving • Consider Symbolic litmus-test verification as driving problem - Application: MP code optimization (synchronization removal) • Non-standard interpretation methods might be able to combine static constraint evaluation and explicit constraint evaluation 31
af3fcf5311fcdfea654122e1246bbf1f.ppt