491727da75b0a24f614ed2a847d57575.ppt
- Количество слайдов: 46

A Toolbox for Online Algorithms Marcin Bieńkowski University of Wrocław phd open 2011

A (short) story about an angry student who was (eventually) right. Marcin Bieńkowski A Toolbox for Online Algorithms 2

What you need course: This are smart tools good tools quite and not smart problemssimple problems for very Marcin Bieńkowski A Toolbox for Online Algorithms 3

What’s in the box? § 10 minute crash course into online algorithms § Toolbox § Potential functions § Work functions § Linear programming § Classify and randomly select Marcin Bieńkowski A Toolbox for Online Algorithms 4

Online algorithms Marcin Bieńkowski A Toolbox for Online Algorithms 5

Online algorithms (1) Optimization problems e. g. set cover, independent set, facility location, TSP, … Approximate solutions for any instance we want scarce computational resources Online problems = input is revealed gradually for any instance we want scarce computational resources + we don’t know the future offline optimum Marcin Bieńkowski A Toolbox for Online Algorithms 6

Online algorithms (2) Deterministic algorithms for any instance we want Randomized algorithms for any instance we want We say that Marcin Bieńkowski is -competitive A Toolbox for Online Algorithms 7

Online algorithms example Ski Rental Problem (SRP) § Each day, in the morning, a skier may § either borrow skis for 1$ § or buy them for B$ § Input: in the evening a skier may break his/her leg § Objective: minimize the total cost Marcin Bieńkowski A Toolbox for Online Algorithms 8

Online algorithms example: SRP (1) 1 -approximation algorithm is trivial: § is the day when skier breaks leg § If T · B, rent all the time § If T > B, buy at the first day For any instance , What about online solutions? Marcin Bieńkowski A Toolbox for Online Algorithms 9

Online algorithms example: SRP (2) Bad (but natural) strategies: § Skier always rents For the instance I where the leg is never broken and § Skier buys at the first day For the instance I where the leg is broken at the first day and Marcin Bieńkowski A Toolbox for Online Algorithms 10

Online algorithms example: SRP (3) Best online strategy: rent for B-1 days and buy at day B. Analysis: If T < B, then If T ¸ B, then this strategy is and -competitive This is the best deterministic online algorithm Marcin Bieńkowski A Toolbox for Online Algorithms 11

Online algorithms example: SRP (4) Best randomized online strategy: § Choose purchase day randomly: day k · B with probability proportional to § For large B the such strategy is -competitive But WHY this probability distribution? ! § Make several observations and solve the system of equations… § … or wait till tomorrow till you see LP-based approach! Marcin Bieńkowski A Toolbox for Online Algorithms 12

World is online Many real life problems have online nature: § network protocols § routing § scheduling § exploration § cache organization § some data structures § financial decisions § and many more Marcin Bieńkowski A Toolbox for Online Algorithms 13

Toolbox Outline 1. Potential functions (PF) 2. Work functions 3. Linear programming 4. Classify and randomly select Marcin Bieńkowski A Toolbox for Online Algorithms 14

PF: a toy problem Problem: List reorganization (singly-linked) C F A D G H B J Input: sequence of the following operations insert(x): inserts x at the end of the list, cost L+1 search(x): finds x on the list, cost = position of x delete(x): deletes x from the list, cost as for search. Model: § After search or insert, ALG may move x towards the front of the list for free. § Afterwards, ALG may swap arbitrary adjacent elements paying 1. Marcin Bieńkowski A Toolbox for Online Algorithms 15

PF: a natural algorithm Algorithm Move To Front (MTF) After each insert(x) or search(x) operation, move x to the beginning of the list (for free). Marcin Bieńkowski A Toolbox for Online Algorithms 16

PF: costs (1) Typical online setting: the problem consists of many rounds. In round : § there is a request § the algorithm serves it and pays What is OPT doing? Besides, computing OPT is OPT? Do I look I care? NP-complete Neither should you! Casual approach: simulate both ALG and OPT (actually any other algorithm) on the same sequence and relate their costs. Marcin Bieńkowski A Toolbox for Online Algorithms 17

PF: costs (2) Typical online setting: the problem consists of many rounds. In round : § there is a request § the algorithm serves it and pays Casual approach: simulate both ALG and OPT (actually any other algorithm) on the same sequence and relate their costs. We want: Showing sufficient, but it is not the case! Marcin Bieńkowski for all steps would be A Toolbox for Online Algorithms 18

PF: introduction to potential We want: Solution: take a potential function 1. 2. where , such that PROOF Does it help? Also known as: How the heck can I guess the correct potential function? There is a rule of the thumb that USUALLY works. Marcin Bieńkowski A Toolbox for Online Algorithms 19

PF: states For many online problems, algorithms are in states and the cost depends on request and state only. State space: ALG OPT Rule of the thumb: Define as a constant times the cost of changing state from ALG to OPT. § Access(x) request § x is at the beginning of OPT § x is at the end of MTF Why does it help (in the bad case)? When is small and is large… … then ALG changes state towards OPT, MTF moves x to the decreasing the potential! beginning of the list Marcin Bieńkowski A Toolbox for Online Algorithms 20

PF: potential for MTF Algorithm Move To Front (MTF): After each insert(x) or search(x) operation, move x to the beginning of the list (for free). Potential function: Inversion: a pair (x, y) such that: § x is before y in MTF list § x is after y in OPT list Potential function = number of inversions Theorem: MTF is 2 -competitive. Marcin Bieńkowski PROOF A Toolbox for Online Algorithms 21

Toolbox Outline 1. Potential functions 2. Work functions (WF) 3. Linear programming 4. Classify and randomly select Marcin Bieńkowski A Toolbox for Online Algorithms 22
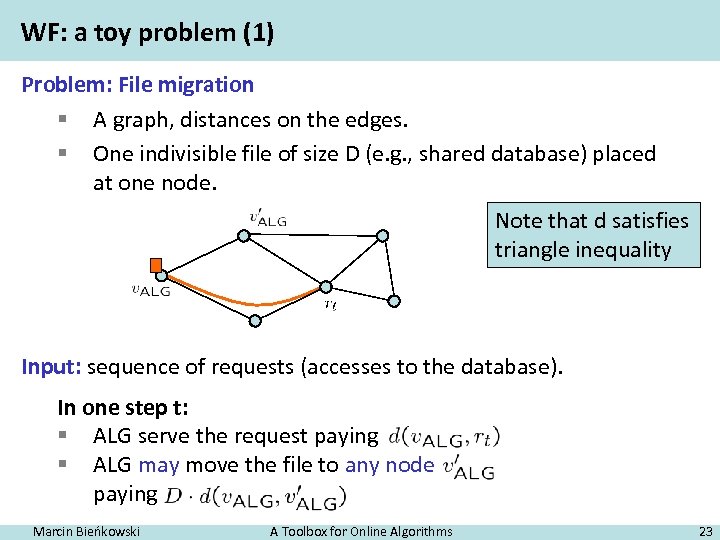
WF: a toy problem (1) Problem: File migration § A graph, distances on the edges. § One indivisible file of size D (e. g. , shared database) placed at one node. Note that d satisfies triangle inequality Input: sequence of requests (accesses to the database). In one step t: § ALG serve the request paying § ALG may move the file to any node paying Marcin Bieńkowski A Toolbox for Online Algorithms 23

WF: a toy problem (2) Let’s make it even simpler § Just two nodes connected by an edge of length 1 § File is initially at node a a Marcin Bieńkowski b Elementary, dear Watson A Toolbox for Online Algorithms 24

WF: randomization Our algorithm will be randomized! a b Behavioral definition: ``At the end of step t, move the file to some random node. ’’ Distributional definition: ``At the end of step t, choose probability distribution nodes, i. e. , file is at v with probability. ’’ over PROOF Lemma: We may emulate distributional definition of ALG by behavioral one. The cost of changing from to is Marcin Bieńkowski A Toolbox for Online Algorithms 25

WF: work functions (1) After t requests, we may compute work function : The optimal cost of serving sequence up to step t and ending with file at node x. Computing the work function Can be computed efficiently by a simple dynamic programming § We assume that ALG may move the file before the input seq. § starting conditions: and Marcin Bieńkowski A Toolbox for Online Algorithms 26

WF: work functions (2) After t requests, we may compute work function : The optimal cost of serving sequence up to step t and ending with file at node x. Relation to OPT § § It does not mean that OPT has the file at such minimizer! § However, we may assume that (the amortized) OPT cost in step t is Marcin Bieńkowski A Toolbox for Online Algorithms 27
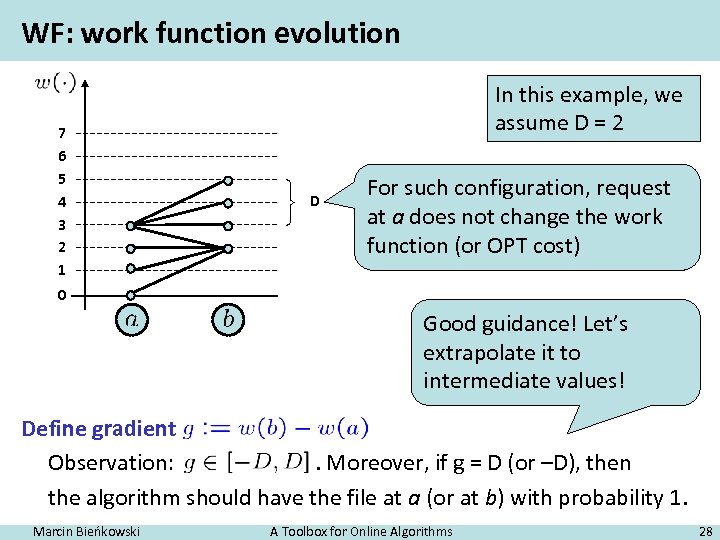
WF: work function evolution 7 6 5 4 3 2 1 In this example, we assume D = 2 D For such configuration, request at a does not change the work function (or OPT cost) 0 Good guidance! Let’s extrapolate it to intermediate values! Define gradient Observation: . Moreover, if g = D (or –D), then the algorithm should have the file at a (or at b) with probability 1. Marcin Bieńkowski A Toolbox for Online Algorithms 28

WF: the algorithm 7 6 5 4 3 2 1 Gradient Recall: D Work Function Algorithm At step t, choose distribution such that and 0 Theorem Work function algorithm is Marcin Bieńkowski , -competitive. A Toolbox for Online Algorithms PROOF 29

Thank you for your attention! (and see you tomorrow) Marcin Bieńkowski A Toolbox for Online Algorithms 30

Toolbox Outline 1. Potential functions 2. Work functions 3. Linear programming (LP) 4. Classify and randomly select Marcin Bieńkowski A Toolbox for Online Algorithms 31
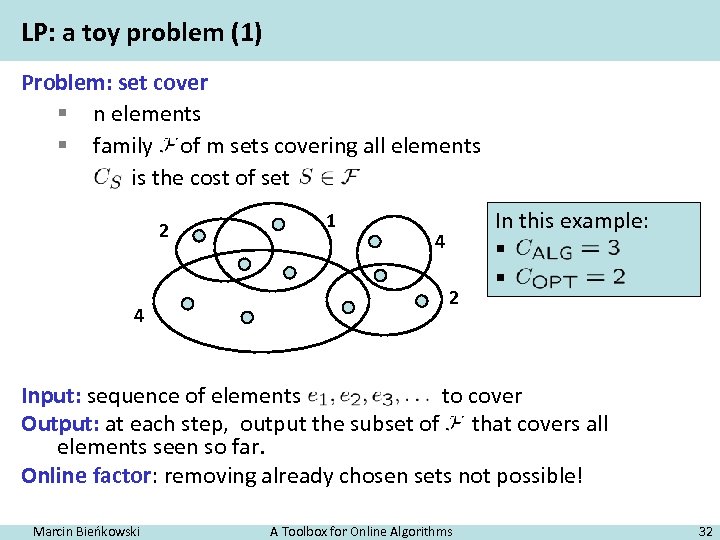
LP: a toy problem (1) Problem: set cover § n elements § family of m sets covering all elements is the cost of set 2 4 1 4 2 In this example: § § Input: sequence of elements to cover Output: at each step, output the subset of that covers all elements seen so far. Online factor: removing already chosen sets not possible! Marcin Bieńkowski A Toolbox for Online Algorithms 32

LP: a toy problem (2) Make the problem easier: FRACTIONAL set cover § n elements § family of m sets covering all elements is the cost of set 2 4 1 4 2 Input: sequence of elements to cover Output: at each step, output the function which covers each already seen element , i. e. , Online factor: removing already chosen fractions of sets not possible! Marcin Bieńkowski A Toolbox for Online Algorithms 33

LP: offline solution (1) What about offline (fractional) solution after step k? § We have to cover elements 1 2 4 Yes, you guessed right, use linear programming! minimize: subject to: (for all 1 · i · k) (for all Marcin Bieńkowski A Toolbox for Online Algorithms ) 34

LP: offline solution (2) Do you recall? § For potential functions we did not care about OPT at all § For work functions, our construction relied heavily on OPT § Are we going to use it now? We may compute it! For the algorithm: NO. For the analysis: YES. Marcin Bieńkowski A Toolbox for Online Algorithms 35

LP: dual program ``If you have an LP, write a dual program and stare at it long enough’’ (quote from a random Stanford professor) Primal program (Pk) Dual program (Dk) min. : max. : subject to: (for all ) ) Strong duality theorem: OPT(Pk) = OPT(Dk) Marcin Bieńkowski A Toolbox for Online Algorithms 36
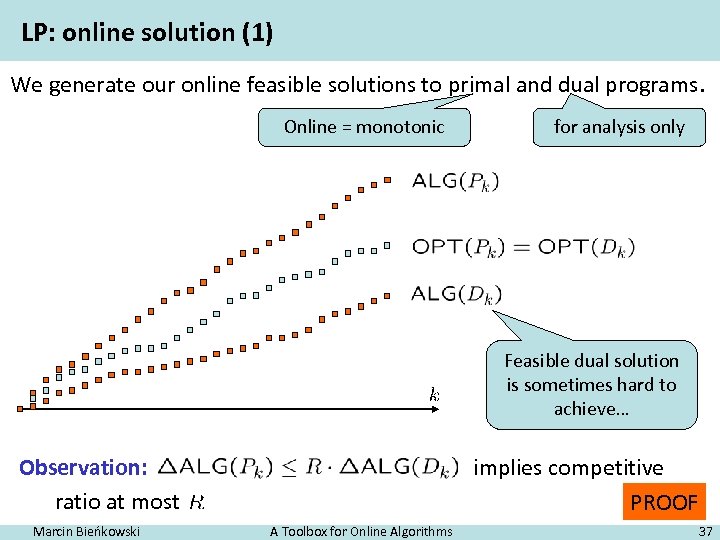
LP: online solution (1) We generate our online feasible solutions to primal and dual programs. Online = monotonic for analysis only Feasible dual solution is sometimes hard to achieve… Observation: ratio at most Marcin Bieńkowski implies competitive PROOF A Toolbox for Online Algorithms 37
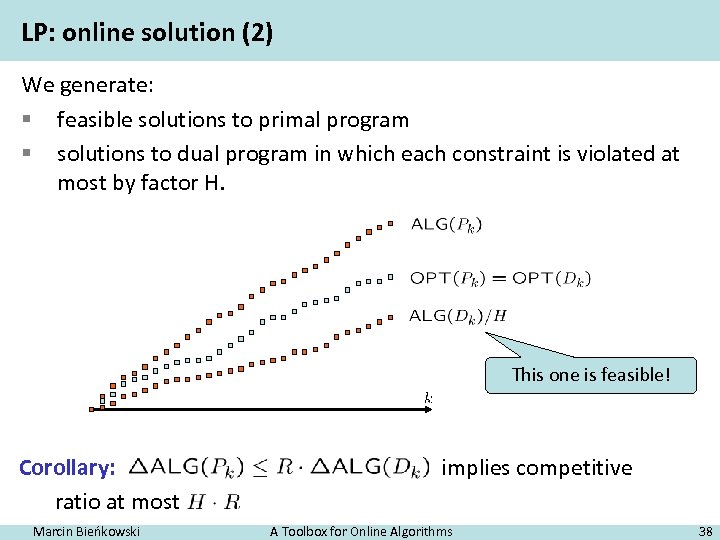
LP: online solution (2) We generate: § feasible solutions to primal program § solutions to dual program in which each constraint is violated at most by factor H. This one is feasible! Corollary: ratio at most Marcin Bieńkowski implies competitive A Toolbox for Online Algorithms 38

LP: the algorithm (1) minimize: Primal program (Pk) subject to: (for all maximize: ) Dual program (Dk) subject to: (for all ) ) Assume we have a solution for Pk-1 Pk contains one extra constraint Algorithm for step k: While : § For each containing let § Observation 2: PROOF Observation 3: Each constraint of the dual solution is violated at most by 1: Generated primal solution is feasible Observationfactor O(log m) TRIVIAL PROOF Marcin Bieńkowski A Toolbox for Online Algorithms 39

LP: the algorithm (2) Observation 1: Generated primal solution is feasible Observation 2: Observation 3: Each constraint of the dual solution is violated at most by factor O(log m) Corollary: ALG is O(2 log m) = O(log m)-competitive Marcin Bieńkowski A Toolbox for Online Algorithms 40

Toolbox Outline 1. Potential functions 2. Work functions 3. Linear programming 4. Classify and randomly select (CRS) Marcin Bieńkowski A Toolbox for Online Algorithms 41
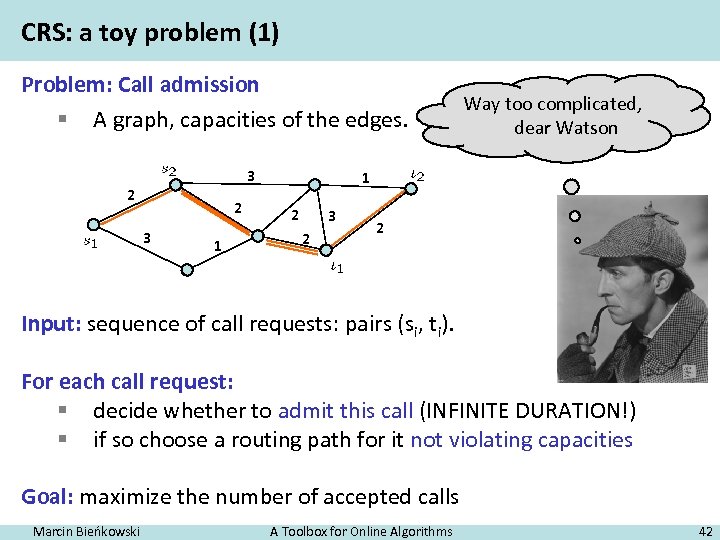
CRS: a toy problem (1) Problem: Call admission § A graph, capacities of the edges. 3 2 2 3 1 Way too complicated, dear Watson 1 2 3 2 2 Input: sequence of call requests: pairs (si, ti). For each call request: § decide whether to admit this call (INFINITE DURATION!) § if so choose a routing path for it not violating capacities Goal: maximize the number of accepted calls Marcin Bieńkowski A Toolbox for Online Algorithms 42

CRS: a toy problem (2) Problem: Call admission on line § A line graph of n nodes § all edges have capacity 1 Input: sequence of call requests: pairs (si, ti). For each call request: § decide whether to admit this call (INFINITE DURATION!) without violating capacities § if so choose a routing path Goal: maximize the number of accepted calls Marcin Bieńkowski A Toolbox for Online Algorithms 43

CRS: deterministic lower bound Lemma: Any deterministic algorithm on n-node line graph has the competitive ratio at least n-1. PROOF For a nontrivial competitive ratio, we need randomization! Marcin Bieńkowski A Toolbox for Online Algorithms 44
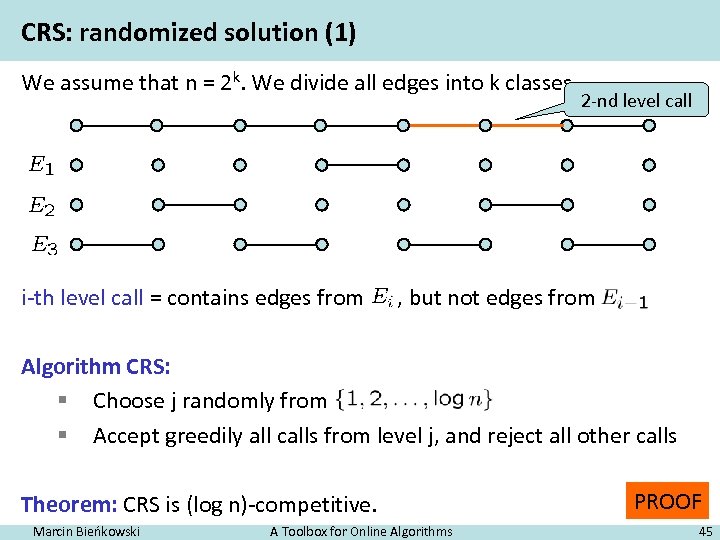
CRS: randomized solution (1) We assume that n = 2 k. We divide all edges into k classes. i-th level call = contains edges from 2 -nd level call , but not edges from Algorithm CRS: § Choose j randomly from § Accept greedily all calls from level j, and reject all other calls Theorem: CRS is (log n)-competitive. Marcin Bieńkowski A Toolbox for Online Algorithms PROOF 45

Thank you for your attention! Marcin Bieńkowski A Toolbox for Online Algorithms 46
491727da75b0a24f614ed2a847d57575.ppt