6af0263d6548c4f519b35496bb6ff1ac.ppt
- Количество слайдов: 54

A survey on the Group Steiner problem Guy Kortsarz, Rutgers Camden

Steiner Tree • A leading (to say the least) researcher said about Steiner Tree: • ‘’A rather un interesting generalization of the Euclidean version” • We need more humilty among theory people. • In practice Multicommodity Buy-at-Bulk is crucial. And it is a many steps generalization of Steiner Tree and Steiner Forrest.

Definitions • Steiner tree. Given an edge weighted graph G(V, E) and a set S V of terminals, find a min cost tree T(V’, E’) that contains all of S. • The Group Steiner Problem is a generalization of this problem. • As we shall see, GSP is ST in case all groups have size 1.

Group Steiner on General Graph • Given a graph G(V, E) with edge costs c(e) and a root r. • A group is a subset Ui of V. • We are given k groups U 1, …. , Uk • The maximum size of a group is m. • A solution is a Tree T(V’, E’), rooted at r so that V’ is a hitting set for {Ui }, namely contains at least one vertex of every Ui

Reduction to trees • • • Fakcharoenpho Rao and Talwar A graph can be mapped to distribution of trees. If we start with a graph G(V, E) the expected cost of en edge (the distance between the two neighbors) does not go down. • The expected length of an edge grows by at most O(log n) factor.

Redcution to a (random) tree • This means by linearity of expectation that the expected optimum is only O(log n) larger than the optimum in the graph • Thus there is a tree with cost at most O(log n) times the optimum of the graph. • This is a reduction from a graph to a tree! • The O(log n) is tight (for expanders as so many times).

Credit • Bartal was the first to give such a result with worse distortion. • Bartal defined the HST namely the cost of edges goes down by a fraction each level. • The FRT improvement and entire algorithm is cool and readable. • For example: alternative O(log n) for minimum cost Multicut of pairs. • Gives some immediate approximation like Buyat-Bulk if the length and the cost are equal.

Group Steiner on trees is nothing but Set Cover with tree costs 3 3 2 10 1 1 1 1

Choosing a Set Cover of size 5 is better than size 1 3 3 2 1 1 1

The approximation of Garg Konjevod and Ravi • They give O(h log k)-approximation algorithm for Group Steiner on trees. • T= (V; E) rooted at r has depth h. • Implies O(log m* log k) ratio. m max size group, k is # of groups. • Simple proof: Grag and Kandekhar. Unpublished. • The GKR result uses LP methods. • Beautiful.
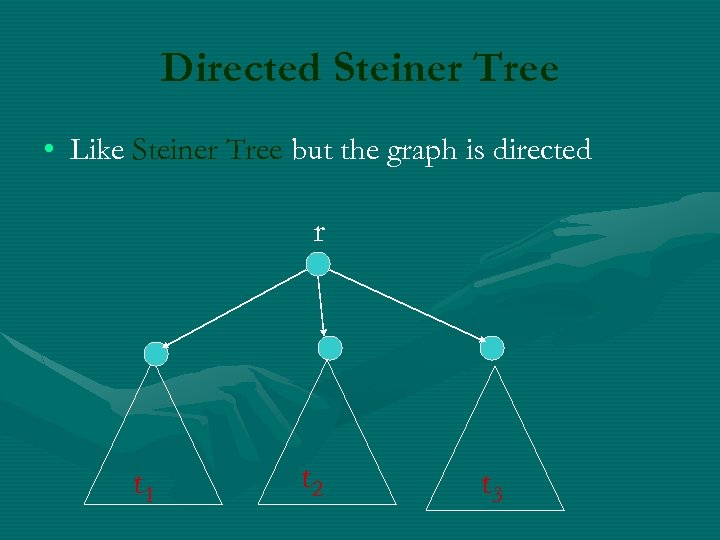
Directed Steiner Tree • Like Steiner Tree but the graph is directed r t 1 t 2 t 3

Choosing a child with good density • There is a subtree with ti/cost(i) at least t/opt, with cost(i) the cost of the subtree including the edge to the root, t the total number of terminals. • K, Peleg: an algorithm for DST (originally for Shallow light trees!). Analysis not the best. • Idea: guess ti and the identity of the child and recusre with these two values. • Charikar et al. Brilliant anylisis of the K, Peleg algorithm.

The ratio of Charikar et al • Charikar et al: The algorithm of K, Peleg has ratio 1/ 3 n for every . Time more than n 1/ • Gives ratio n for every constant • Interesting is plugging =1/log n • O(log 3 n) ratio at quasi polynomial time. • The technique is called Recursive Greedy. • Invented independently by Zelikovsky • But Charikar et al, used our algorithm word by word.

Directed Steiner Tree • • • I will present a non recursive greedy solution Using GST An important theroem by Zelikovsky: Take transitive closure. Among all trees of height at most 1/ there is a solution of cost at most (1/ )3 * n 1/

Alternative approximation algorithm for Directed Steiner • Create a graph H in which each path from the root r to some u of length at most 1/ , is a node. • There is a directed edge from p’ to p if p extends p’ by one edge. • By theorem of Zelikovsky, a solution of cost at most O(n 1/ )opt is embedded in H.

A non recursive greedy approximation for Directed Steiner • For every terminal t, make a group Ht of all paths of length at most 1/ that start at r and end at t. • This reduces the problem to Group Steiner on trees: Connect at least one terminal of Ht by a path from r , for every t.

Directed Steiner tree • This gives a non Recursive Greedy algorithm for Directed Steiner with same ratio: n . Need to teach GST. But the proof of Garg et al relatively easy. • The space complexity ~ n 1/. • And of course so is the time complexity, but unfortunately, that the best known.

GSF with application for Directed Steiner Forest • The input is an undirected graph G(V, E) with costs ce on edges. • The input also contains a collection of set pairs {Si, Ti} for i=1 to k. • The goal is to select a minimum cost subgraph G(V, E’) so that for every i there is some si Si and ti Ti that are in the same connected component.

An example with uniform weights S 1 T 1 S 2 T 2 S 3 T 3
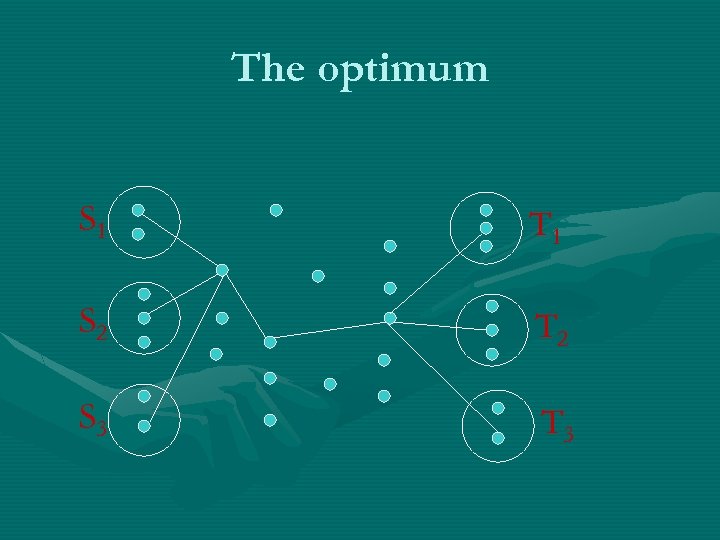
The optimum S 1 T 1 S 2 T 2 S 3 T 3

Approximation ratio • A paper by Chandra, Even, Gupta and Segev gives an O(log 4 n) approximation for the problems. • This uses so called density LP. • This means that every pair of sets is covered within some fraction smaller than 1. • Uses the concept of Junction Trees, shown later.

Directed Steiner Forest • Input: A directed graph G(V, E) with a collection of pairs {si, ti} and cost over the edges. • Find: a subgraph G(V, E’) of minimum cost so that for every {si, ti}, there is a directed path in G(V, E’) from si to ti. • The next construction (in a more complicated way) was presented in a paper by Chekuri, Even, Gupta and Segev.

Reduction DSF to GST • A junction tree is an “in directed’’ tree into r from some X={si} and addition to an “out tree’’ into the sinks of X. • Say that there is a junction tree with good density. How do we find it? • We create the same graph that we created for Directed Steiner Tree. • Make all paths that start at si a Set Si. • Make all paths that start at ti a Set Ti.

This gives a GSF instance • By applying the Zelikovsky theorem twice and the O(log 4 n) ratio, gives the density of the junction tree times n. • The graph is directed but all edges are directed into the same direction. • This means that the GSF instance still admits O(log 4 n) ratio approximation. • One of three tools used to approximate DSF.
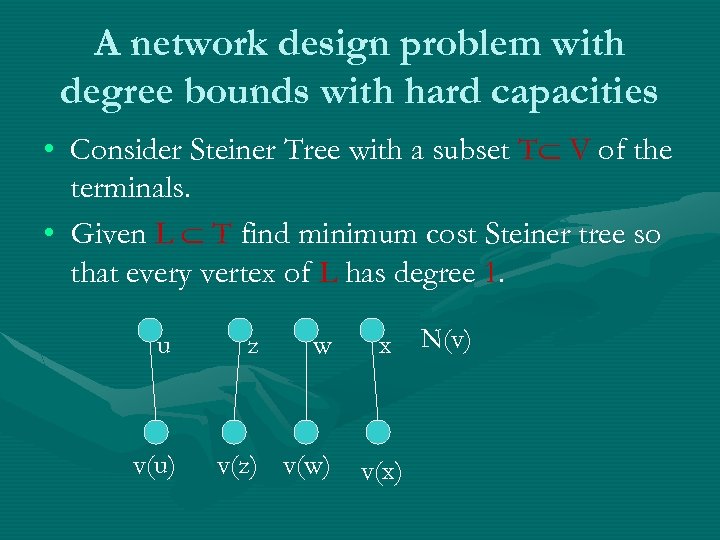
A network design problem with degree bounds with hard capacities • Consider Steiner Tree with a subset T V of the terminals. • Given L T find minimum cost Steiner tree so that every vertex of L has degree 1. u v(u) z w v(z) v(w) x v(x) N(v)

Solution • You can remove every v L from the graph. • The vertex v can not connect two other vertices. • The groups will say which vertex is the neighbor of every v L
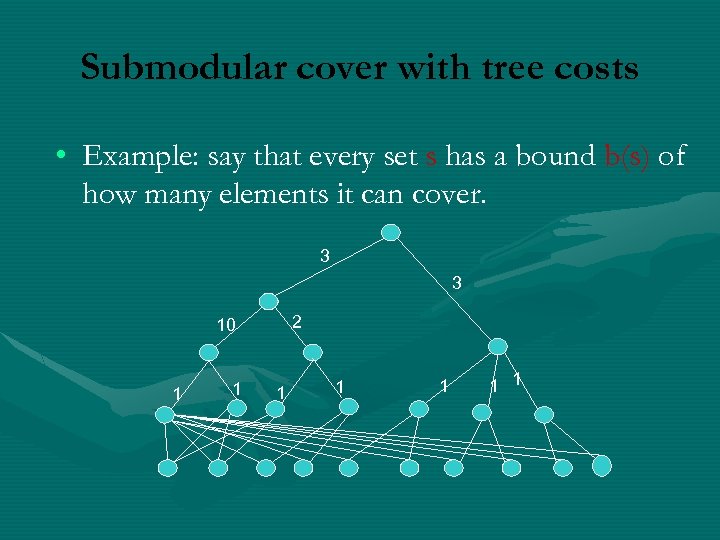
Submodular cover with tree costs • Example: say that every set s has a bound b(s) of how many elements it can cover. 3 3 2 10 1 1 1 1

Submodular cover with tree costs • Given a candidate solution, we can compute if feasible with flow computation 3 3 2 10 1 1 1 1
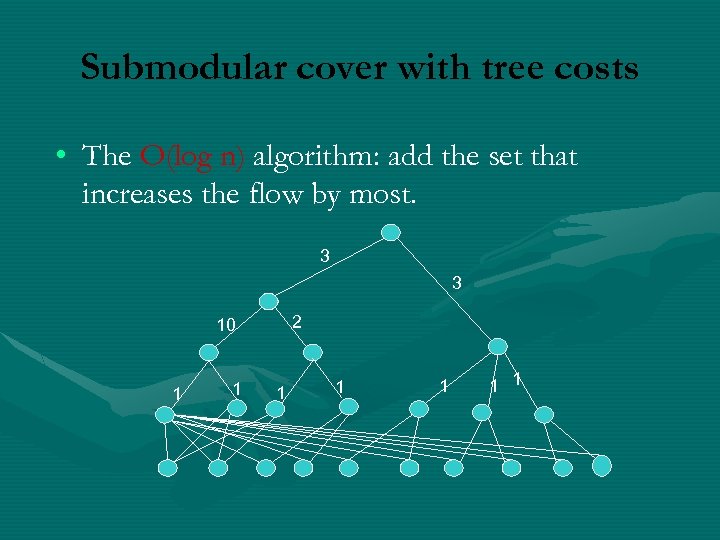
Submodular cover with tree costs • The O(log n) algorithm: add the set that increases the flow by most. 3 3 2 10 1 1 1 1

Submodular cover with tree costs • If all vertices have degree bound 1 but the high degree vertex whose b(x)= 3 3 2 10 x 1 1 1 1
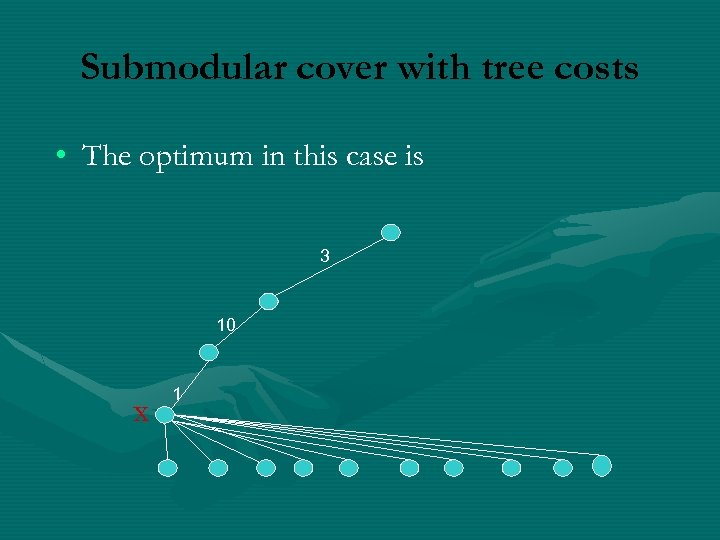
Submodular cover with tree costs • The optimum in this case is 3 10 x 1

A different approximation than GKR • Chekuri Even and K, recursive greedy algorithm for GST. • We “improve to the worse” GKR by giving (log n)(2+ ) ratio. • The reason for the algorithm that it is combinatorial. Solves an open problem of GKR • But also seems more flexible.

Used to solve the problem we discussed • Gives around (log n)3 for Submodular cover with tree costs. • GKR does not work for this • In another paper, we gave (log n)3 for Submodular Cover with tree costs. I was sure nobody did because the CEK is highly complex. • Found out that Calinesco, Zelikovsky did it before us.

Used to solve the problem we discussed • Gives around (log n)3 for Submodular cover with tree costs. • GKR does not work for this • In another paper, we gave (log n)3 for Submodular Cover with tree costs. I was sure nobody did because the ECK is highly complex. • Found out that Calinesco, Zelikovsky did it before us. • Please: Can you work on someone else’s problems?
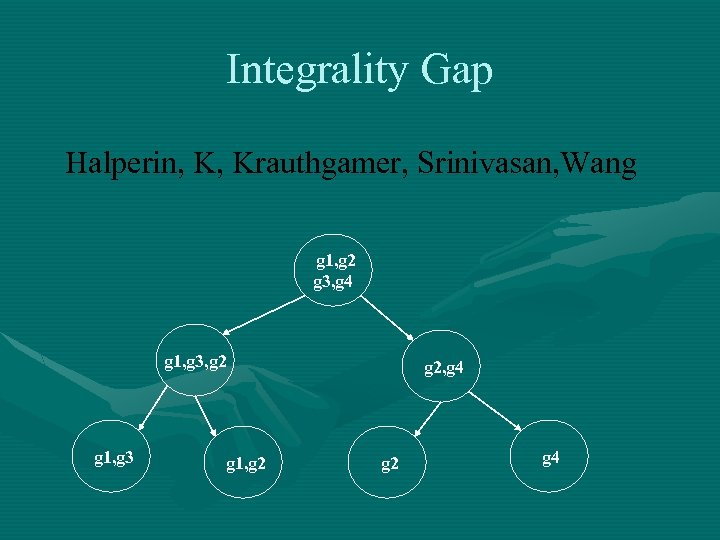
Integrality Gap Halperin, K, Krauthgamer, Srinivasan, Wang g 1, g 2 g 3, g 4 g 1, g 3, g 2 g 1, g 3 g 1, g 2, g 4 g 2 g 4
![Analysis: • The costs need to decrease by constant factor [HST] • The fractional Analysis: • The costs need to decrease by constant factor [HST] • The fractional](https://present5.com/presentation/6af0263d6548c4f519b35496bb6ff1ac/image-36.jpg)
Analysis: • The costs need to decrease by constant factor [HST] • The fractional value is the same at every level • Thus, if the height is H then the fractional is O (H ) • The integral H 2 log k (k is # groups) • (log k)2 gap as H=log k • We now show an (log k)2 ratio for HST.

Algorithm • Take only log k first layers. First layer edges cost 1. • For every vertex assign it all groups in its subtree • Apply GKR. Gives H*log k namely, (log k)2 • Given that v was chosen we add a path from v to each group v is responsible to. • Only the first edge counts (HST) • And its value is at most 1/k

Hardness • Halperin Krauthgamer: Ω(log 2 - n) hardness. • CEK: O(log 2 n)/loglog(n)) ratio in quasi polynomial time. • HK used the integrality gap as a black bok • Used the upper bound of GKR when proving the lower bound. • First polylog inapproximability. • Maybe the right ratio is O(log 2 n/loglog n) ?

Covering Steiner Tree • For every Group a number xi of vertices that need to be covered from group gi • O(log 2 n) by Konjevod, Ravi Srinivasan. • The following due to Even, K, Slany: for every group create xi Bins • Create a new GS (not CS) instance by randomly putting the vertices of gi in the bins. • The probability that a bin has no optimal terminal: (1 -1/xi)xi<1/e

Solve the 1/2 -group Steiner problem • • Namely cover ½ of the groups. Expected cost O(log n)*opt Gives O(log n)2 ratio. Interesting derandomization: Universal Hash Functions.

Generalization of Group Steiner • Naturally, Directed Steiner tree. • In the case we can add directed edges from all terminals of a group to a new vertex, which is now a terminal to cover • The old difficulty is that in the undirected case this create shortcuts. • GST has been shown to be a special case of Fixed Cost k Flow.

Fixed Cost k-Flow • You have a flow network with costs ce over the edges, and capacities over the edges. • The problem requires sending k flow units from the source to the sink. • The cost is the sum of costs of edges that carry at least one flow unit. • GST being a special case was shown by Hajiaghayi, Khandekar, K, and Nutov
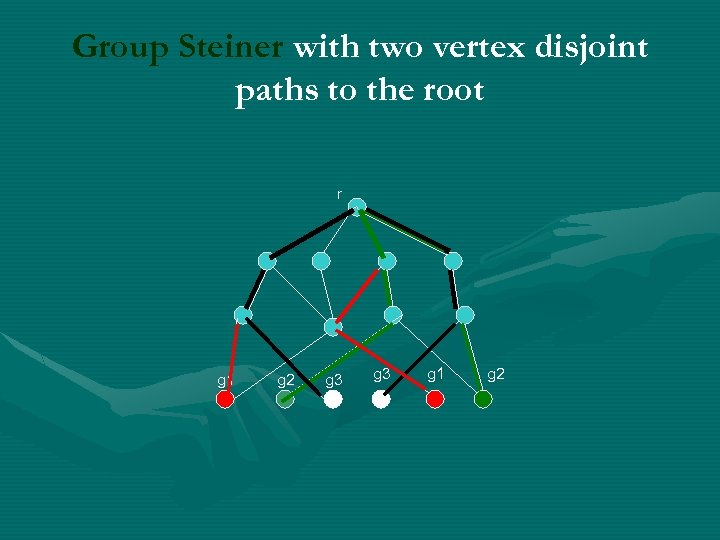
Group Steiner with two vertex disjoint paths to the root r g 1 g 2 g 3 g 1 g 2

Group Steiner with fault tolerance • • • I shall consider a toy problem. Say that all groups have size 2. And we want two edge disjoint paths from the two terminals to r. • This explain an important technique.

Violated sets Say that X V is violated if there is only one edge leaving X, but there should be two edges leaving X (i. e. , X does not contain r but contains a group). Claim: If X and Y are violated, either X U Y and X ∩ Y are both violated, or X-Y and Y-X are both violated.

Why are violated sets uncrossable? For any violated set X, the set X ∩ T must be a sub-tree of T containing an entire group. Plus some non terminals not in T gi X∩T Subtrees are laminar! (i. e. , either two subtrees are disjoint or one is contained in the other. )
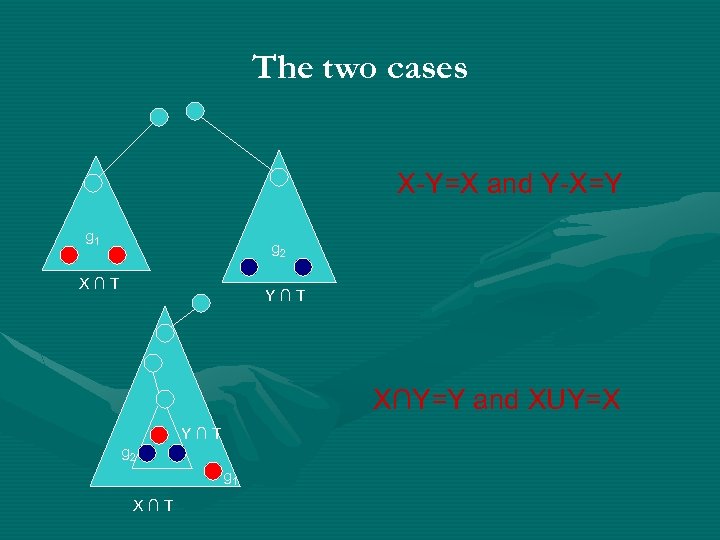
The two cases X-Y=X and Y-X=Y g 1 g 2 X∩T Y∩T X∩Y=Y and XUY=X Y∩T g 2 g 1 X∩T

Consequence The problem of finding a minimum cost cover of an uncrossable family admits 2 approximation (Primal-Dual) [Goemans, Goldberg, Plotkin, Shmoys, Tardos 94]. Therefore, overall we get +2 with the constantly changing best ratio for the unweighted Steiner tree problem.
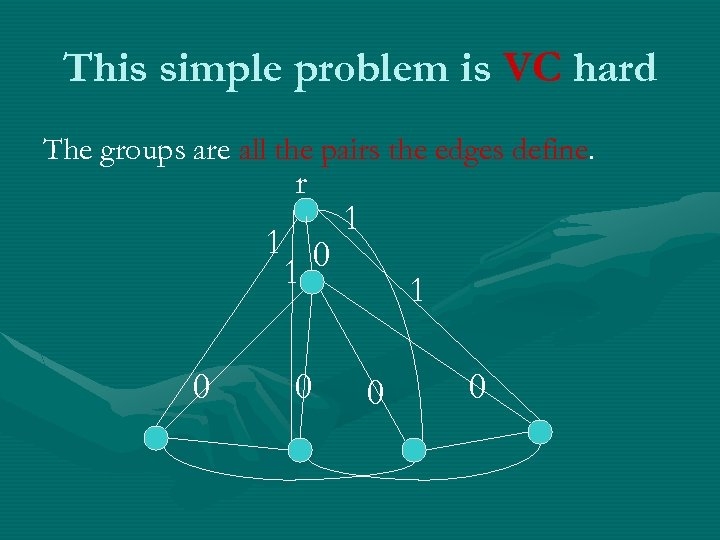
This simple problem is VC hard The groups are all the pairs the edges define. r 1 0 0 1 1 0 0
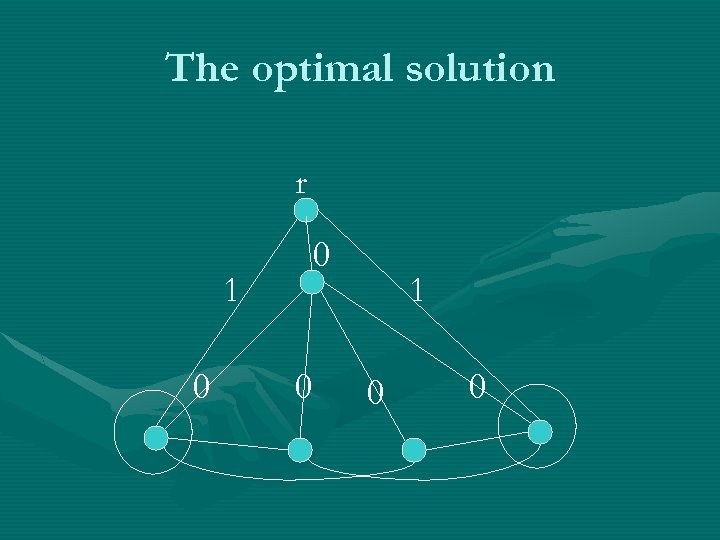
The optimal solution r 0 1 0 0

Fault Tolerant GS • Kandekhar, K, Nutov: O(sqrt{n}) ratio for vertex disjoint paths. • Quite non trivial. • Edge disjoint is easier. Uses the embedding of Elkin et al, namely distribution on spanning trees. By A. Gupta R. Krishnaswamy R. Ravi • O(log 4 n) ratio

Summary • The recursive greedy algorithm for Group Steiner is quite flexible. • It was also used for a problem that combines GS and facility location. • Group Steiner appears when solving other problems • It is highly flexible with respect to generalizations….

Open Problems • Is there a polylog ratio algorithm for GS on graphs without tree embedding? • Is there an O(log 2 n) ratio for GS on graphs? • Is there an O(log 2 n/loglog n) ratio for GS on trees? The integrality gap must have degrees log n which means height log n/loglog n. • Prove under some assumption that Directed Steiner Tree has no polynomial time, polylog ratio approximation(? )

Thanks!
6af0263d6548c4f519b35496bb6ff1ac.ppt