A study of the career paths of hotel

A study of the career paths of hotel general managers sent questionnaires to a SRS of hotels. The average time these 114 general managers had spent with their current company was 11. 78. Construct & interpret a 98% confidence interval for the mean number of years spent with their company if the standard deviation is known to be 3. 2 years. A company found that of the 84 applicants whose credentials were checked, 15 lied about having a degree. Calculate a 90% confidence interval for the true proportion of applicants who lie about having a degree.

A study of the career paths of hotel general managers sent questionnaires to a SRS of hotels. The average time these 114 general managers had spent with their current company was 11. 78. Construct & interpret a 98% confidence interval for the mean number of years spent with their company if the standard deviation is known to be 3. 2 years.

A company found that of the 84 applicants whose credentials were checked, 15 lied about having a degree. Calculate a 90% confidence interval for the true proportion of applicants who lie about having a degree.

Hypothesis Tests & Procedures & Errors Section 9. 1

Confidence & Significance Tests n Confidence Interval ¨ Goal n is to estimate a population parameter Significance Test (Hypothesis Test) ¨ Goal is to assess the evidence provided by data about some claim concerning a population.

Card Activity Guess the proportion of red cards n Draw cards and make an estimate of the proportion of red cards. n Do you want to make an alternate guess? n

Hypothesis n It’s a statement about the value of a population’s characteristic. n Possible hypothesis: n Not Possible:

Test Procedure – Test of Hypothesis n It’s a method for using sample data to decide between 2 competing claims about a characteristic of a population such as a mean or a proportion.

Two Claims n Null Hypothesis ¨ Claim about a population characteristic that is initially assumed to be true. ¨ It’s accepted until proven otherwise. ¨ It represents no change n Alternative Hypothesis ¨ Competing claim – represents change ¨ Has the burden of proof

n Paramedics need to respond to accidents as quickly as possible – they need medical attention within 8 minutes of the crash. One city found that their response time last year was 6. 7 minutes with st. dev of 2 minutes. This year, they selected a SRS of 400 calls and found the response time was 6. 48 minutes. Do these data provide good evidence that response times have decreased since last year?

Example n Nutritionists claim the average number of calories in a serving of popcorn is 70. You suspect it is higher. Implied in this statement is

Format

Example n Machine is calibrated to achieve design specification of 3 inches – diameter of a tennis ball. We are concerned that it is no longer the case.

Example n The company who makes M&M’s says that 30% of the M&M’s that they produce are green. You suspect that it is less than that.

Hypothesis Test n It’s only capable of showing strong support for the Alternate Hypothesis by rejecting the Null Hypothesis. n When the Null is not rejected we simply say that we failed to reject the Null. It doesn’t mean that it’s accepted – only that we’re unable to prove otherwise.

n Just as a jury may reach a wrong decision, testing Hypothesis with sample data may lead us to the wrong conclusion

Error – Risk of error is the price researchers pay for basing inference on a sample. n Type I Error ¨ Reject n the Ho and it was really true Type II Error ¨ Fail to reject the Ho and you should have.

n Type I Error ¨ Result: n Type II Error ¨ Result:

U. S. Dept. of Transportation reported that 77% of domestic flights were “on time. ” The Airline company offers a bonus if their ontime flights exceeds the 77%. n Hypothesis n Type I Error n Type II Error

Salmonella contamination for chicken is 20%. If the salmonella rate is more, the chicken is rejected because it can make people extremely sick. n Hypothesis n Type I Error n Type II Error

Level of Significance n It’s the probability of a Type I error n We use the symbol – n Type II error is represented as

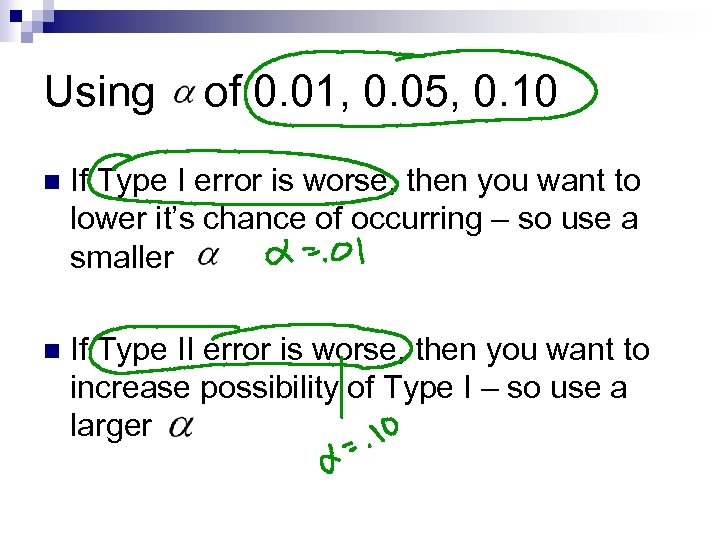Using of 0. 01, 0. 05, 0. 10 n If Type I error is worse, then you want to lower it’s chance of occurring – so use a smaller n If Type II error is worse, then you want to increase possibility of Type I – so use a larger

Homework n Page 546 (1 -10) odd, (19 -21) odd (27, 29)