A Structural Overview of Ordering in Substituted Bismuth

A Structural Overview of Ordering in Substituted Bismuth Oxide Based Solid Electrolytes Isaac Abrahams Materials Research Institute, School of Biological and Chemical Sciences Queen Mary, University of London, UK

Co-authors Funding and Facilities Polish Ministry of Science STFC, ISIS-Facility, Royal Society S.C.M. Chan, A. Kyriacou, S. Ahmed Queen Mary University of London M. Leszczynska, M. Struzik, M. Krynski, F. Krok, Warsaw University of Technology, Poland S. Hull ISIS Facility, Rutherford Appleton Laboratory, UK S.T. Norberg Chalmers University of Technology, Gothenburg, Sweden

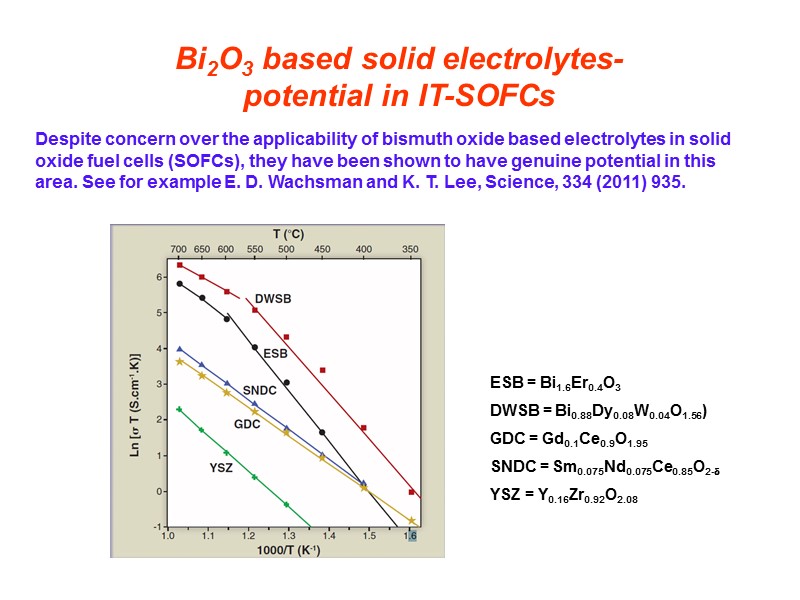
Bi2O3 based solid electrolytes- potential in IT-SOFCs Despite concern over the applicability of bismuth oxide based electrolytes in solid oxide fuel cells (SOFCs), they have been shown to have genuine potential in this area. See for example E. D. Wachsman and K. T. Lee, Science, 334 (2011) 935. ESB = Bi1.6Er0.4O3 DWSB = Bi0.88Dy0.08W0.04O1.56) GDC = Gd0.1Ce0.9O1.95 SNDC = Sm0.075Nd0.075Ce0.85O2- YSZ = Y0.16Zr0.92O2.08

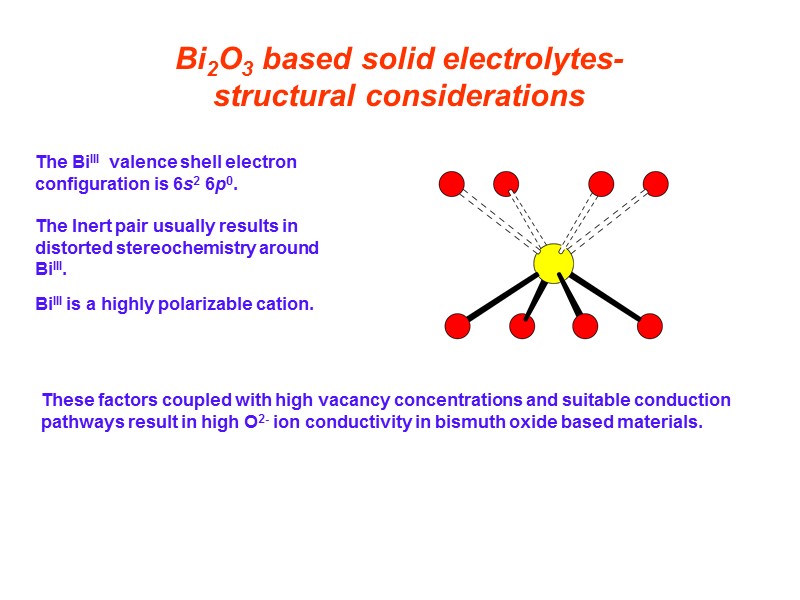
Bi2O3 based solid electrolytes-structural considerations These factors coupled with high vacancy concentrations and suitable conduction pathways result in high O2- ion conductivity in bismuth oxide based materials. The BiIII valence shell electron configuration is 6s2 6p0. The Inert pair usually results in distorted stereochemistry around BiIII. BiIII is a highly polarizable cation.

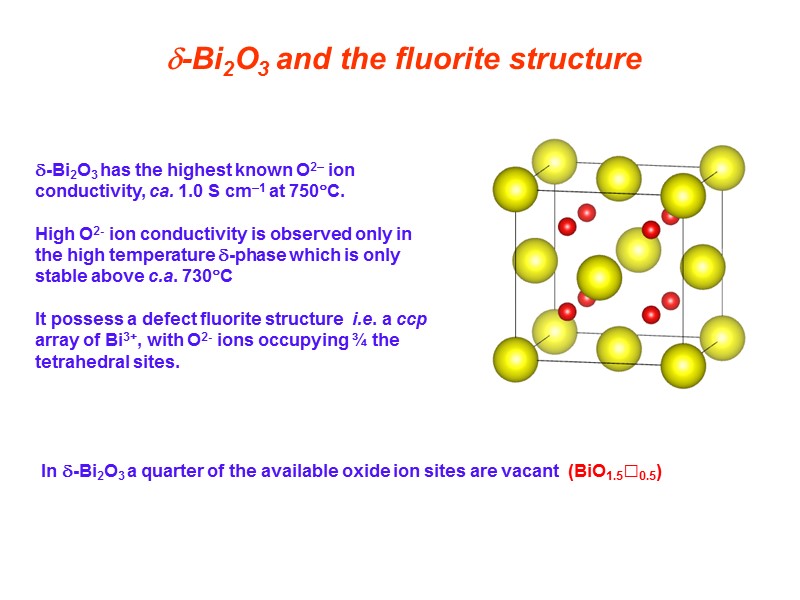
-Bi2O3 and the fluorite structure In ­-Bi2O3 a quarter of the available oxide ion sites are vacant ­ (BiO1.5□0.5) -Bi2O3 has the highest known O2– ion conductivity, ca. 1.0 S cm–1 at 750C. High O2- ion conductivity is observed only in the high temperature ­-phase which is only stable above c.a. 730C It possess a defect fluorite structure i.e. a ccp array of Bi3+, with O2- ions occupying ¾ the tetrahedral sites.

Supervalent substitution in Bismuth Oxide Supervalent substitution in Bi2O3 often leads to superlattice ordering .These can be classified into four basic types with a number of subtypes (Zhou et al, Ling et al) Type ordering Sp. Grp Cell dimensions Eg Type I 2 x 2 x 2 Im-3m a  11.1 Å Bi15TaO25 Type II incommensurate Bi3TaO7 Type III 3 x 3 x 7 I-4m2 a  11.5 Å, c  38.6Å Bi3NbO7 Type IV Aurivillius Mono a  22.7, b  3.85, c  19.26 Å B31Ta17O89   101.9 Selected subtypes Type Ia I4/m a  8.7 Å, c  17.3Å Bi14WO24 Type Ib I41 a  12.5 Å, c  11.3Å Bi22W4O45 Type II* C1 a  34.0, b  7.6, c  6.6 Å Bi7Ta3O18   90.1,   109.1,   90.0

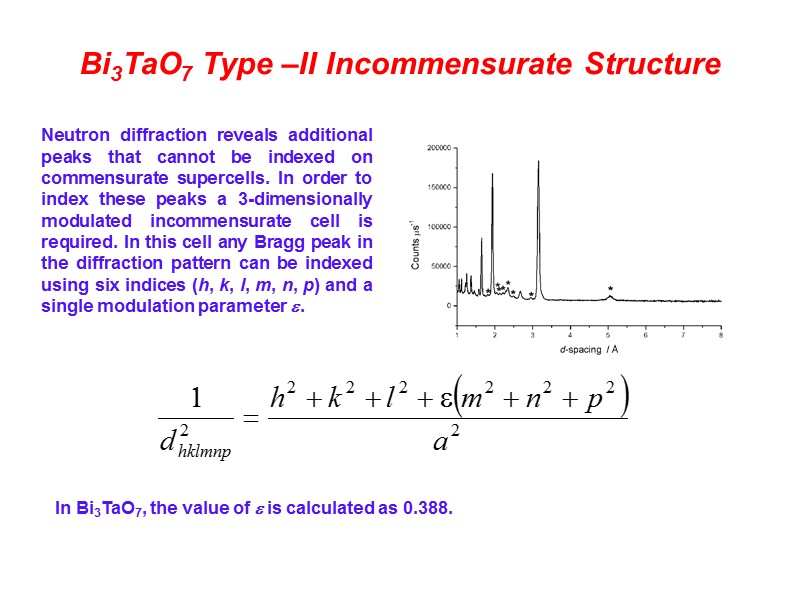
Bi3TaO7 Type –II Incommensurate Structure Neutron diffraction reveals additional peaks that cannot be indexed on commensurate supercells. In order to index these peaks a 3-dimensionally modulated incommensurate cell is required. In this cell any Bragg peak in the diffraction pattern can be indexed using six indices (h, k, l, m, n, p) and a single modulation parameter . In Bi3TaO7, the value of  is calculated as 0.388.

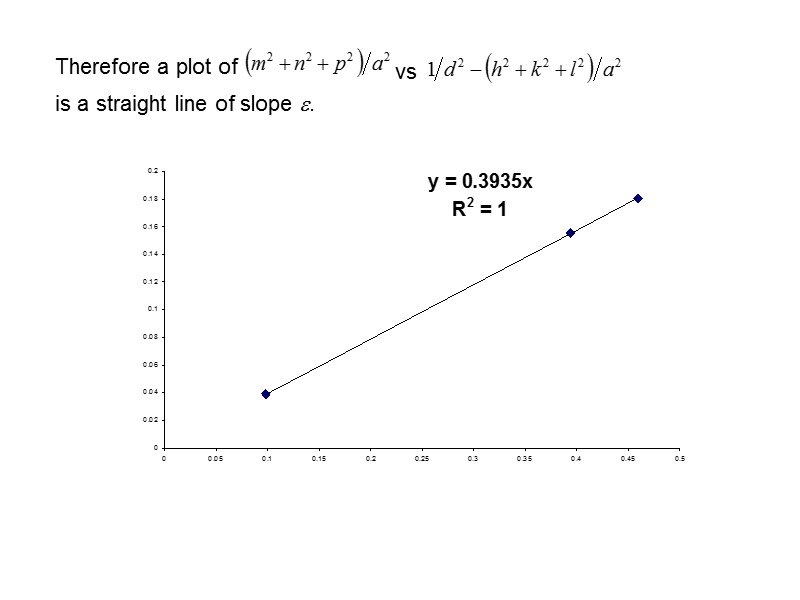
Therefore a plot of vs is a straight line of slope .

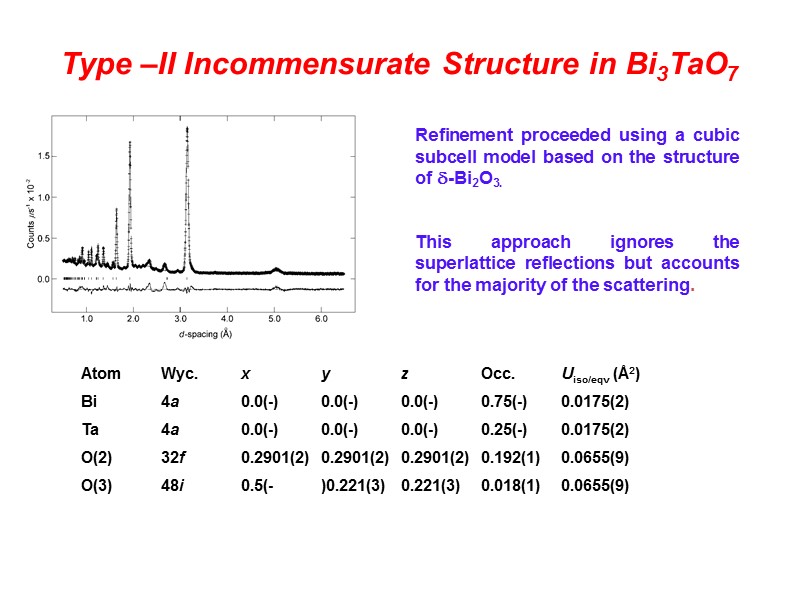
Type –II Incommensurate Structure in Bi3TaO7 Refinement proceeded using a cubic subcell model based on the structure of -Bi2O3. This approach ignores the superlattice reflections but accounts for the majority of the scattering. Atom Wyc. x y z Occ. Uiso/eqv (Å2) Bi 4a 0.0(-) 0.0(-) 0.0(-) 0.75(-) 0.0175(2) Ta 4a 0.0(-) 0.0(-) 0.0(-) 0.25(-) 0.0175(2) O(2) 32f 0.2901(2) 0.2901(2) 0.2901(2) 0.192(1) 0.0655(9) O(3) 48i 0.5(- )0.221(3) 0.221(3) 0.018(1) 0.0655(9)

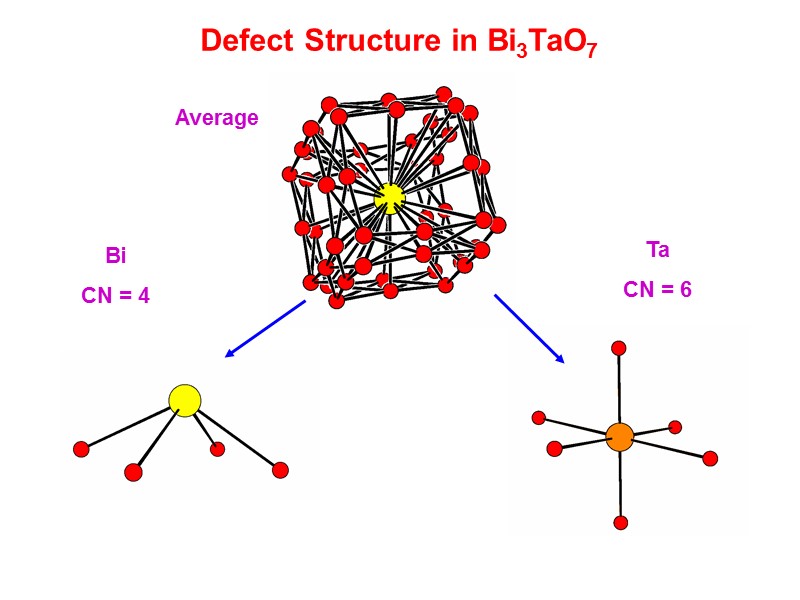
Defect Structure in Bi3TaO7 Average Ta CN = 6 Bi CN = 4

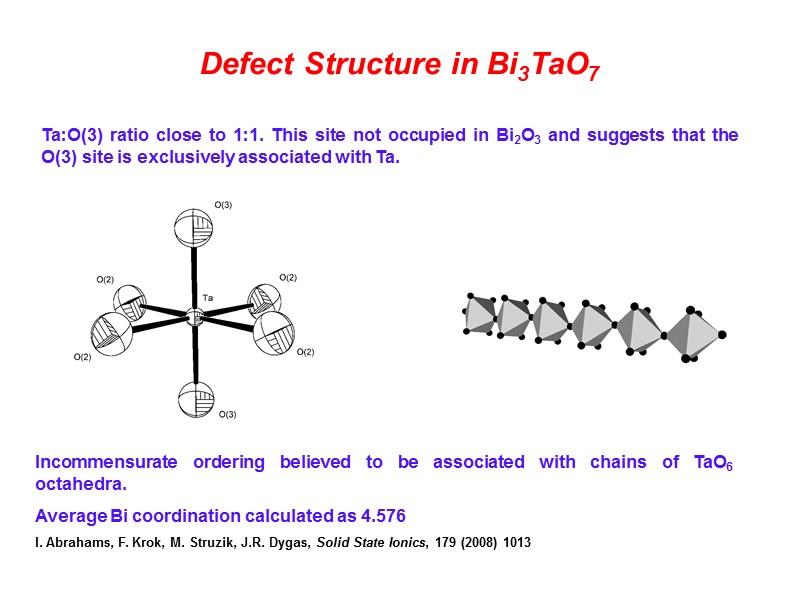
Defect Structure in Bi3TaO7 Ta:O(3) ratio close to 1:1. This site not occupied in Bi2O3 and suggests that the O(3) site is exclusively associated with Ta. Incommensurate ordering believed to be associated with chains of TaO6 octahedra. Average Bi coordination calculated as 4.576 I. Abrahams, F. Krok, M. Struzik, J.R. Dygas, Solid State Ionics, 179 (2008) 1013

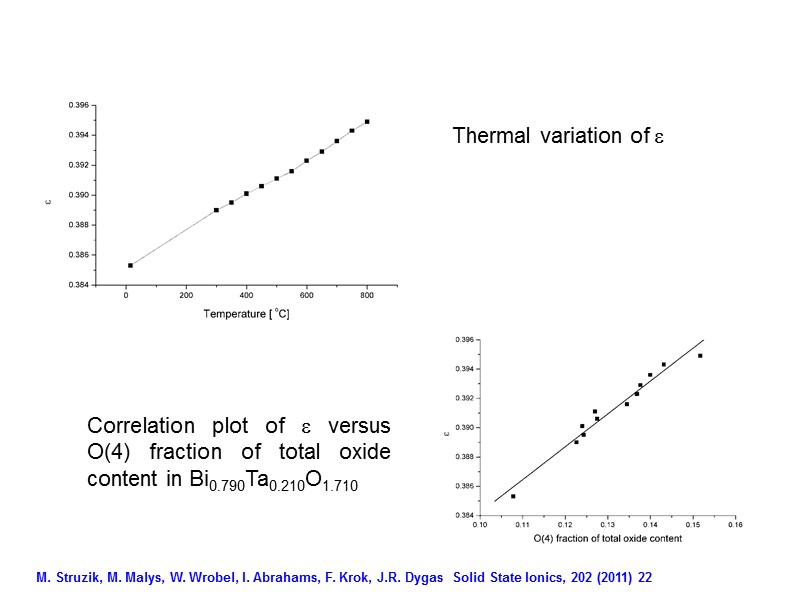
Thermal variation of  Correlation plot of  versus O(4) fraction of total oxide content in Bi0.790Ta0.210O1.710 M. Struzik, M. Malys, W. Wrobel, I. Abrahams, F. Krok, J.R. Dygas Solid State Ionics, 202 (2011) 22

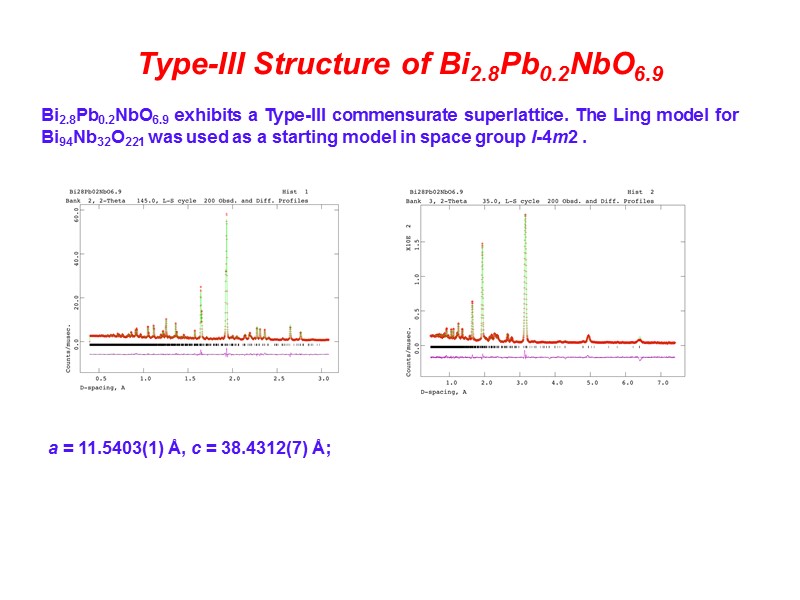
Type-III Structure of Bi2.8Pb0.2NbO6.9 Bi2.8Pb0.2NbO6.9 exhibits a Type-III commensurate superlattice. The Ling model for Bi94Nb32O221 was used as a starting model in space group I-4m2 . a = 11.5403(1) Å, c = 38.4312(7) Å;

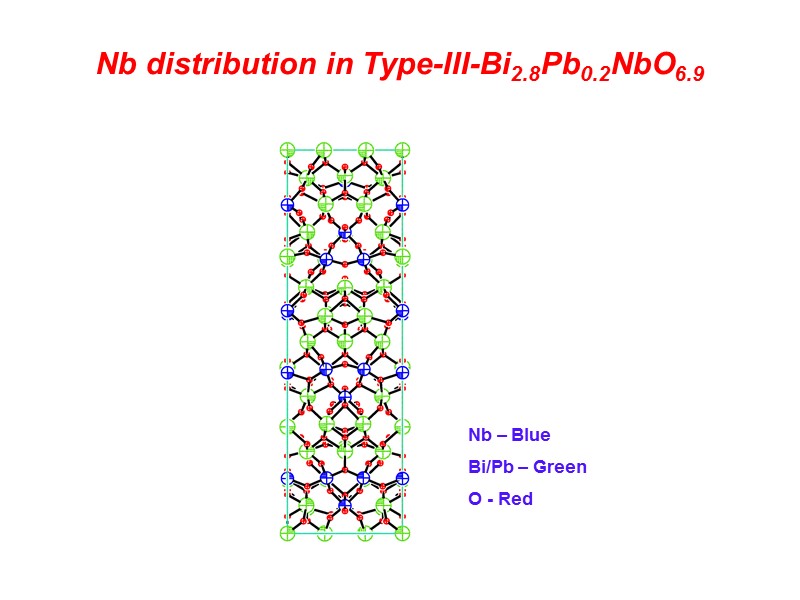
Nb distribution in Type-III-Bi2.8Pb0.2NbO6.9 Nb – Blue Bi/Pb – Green O - Red

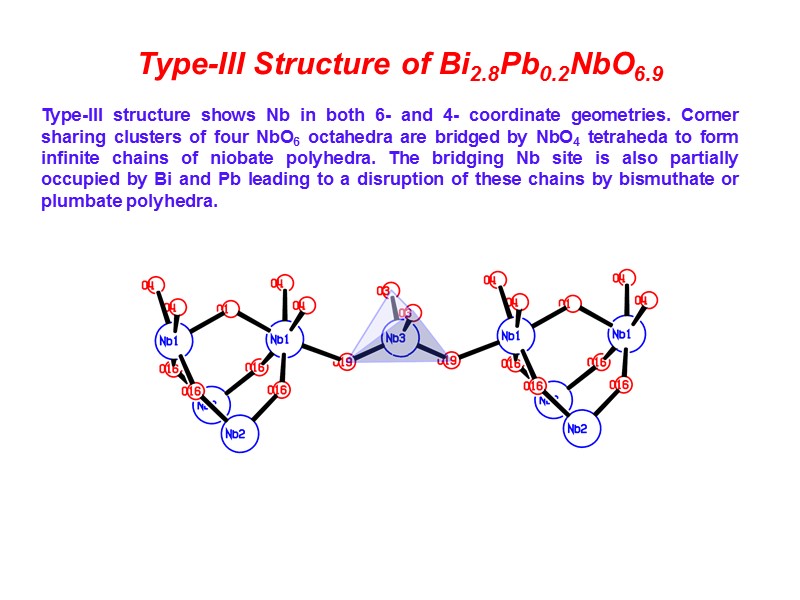
Type-III Structure of Bi2.8Pb0.2NbO6.9 Type-III structure shows Nb in both 6- and 4- coordinate geometries. Corner sharing clusters of four NbO6 octahedra are bridged by NbO4 tetraheda to form infinite chains of niobate polyhedra. The bridging Nb site is also partially occupied by Bi and Pb leading to a disruption of these chains by bismuthate or plumbate polyhedra.

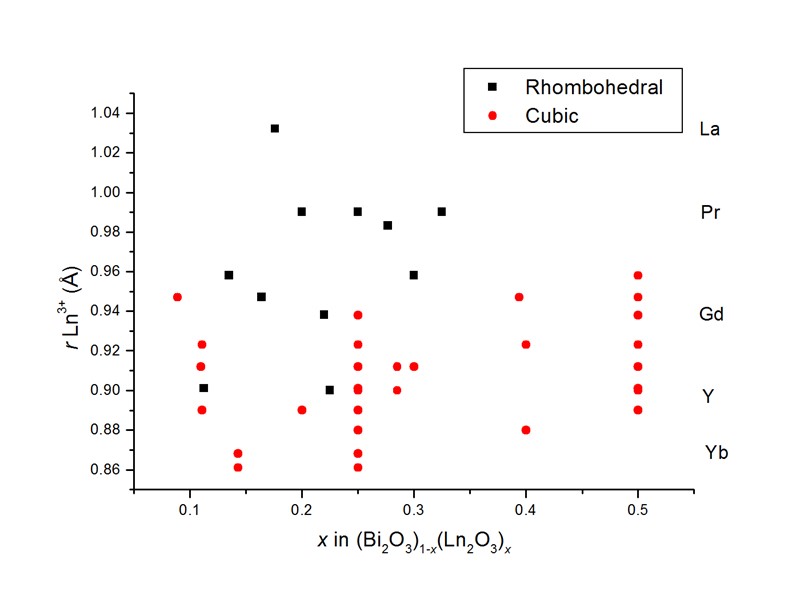
Isovalent substitution in Bi2O3 A variety of cations can be successfully substituted for Bi3+ to yield a “stabilized” fluorite type phase at room temperature. The most common type of substitution involves isovalent lanthanides i.e. (Bi2O3)1-x(Ln2O3)x At low levels of substitution tetragonal -Bi2O3 type phases are often seen. As the level of substitution increases, two main phases are seen viz: a cubic fcc phase Fm-3m, a  5.4 Å a rhombohedral phase R-3m, a  4.0 Å, c  27.4 Å Which phase is observed depends mainly on temperature and the radius of the substituting cation.

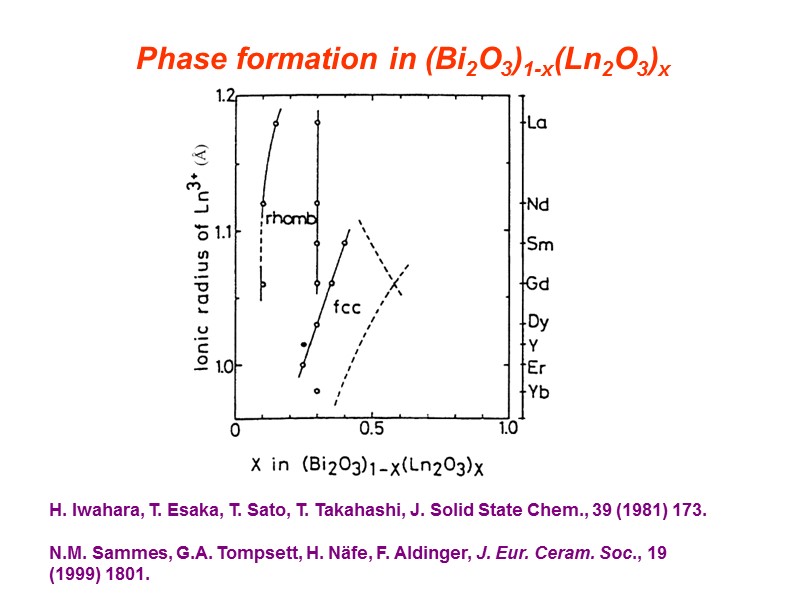
Phase formation in (Bi2O3)1-x(Ln2O3)x H. Iwahara, T. Esaka, T. Sato, T. Takahashi, J. Solid State Chem., 39 (1981) 173. N.M. Sammes, G.A. Tompsett, H. Näfe, F. Aldinger, J. Eur. Ceram. Soc., 19 (1999) 1801.

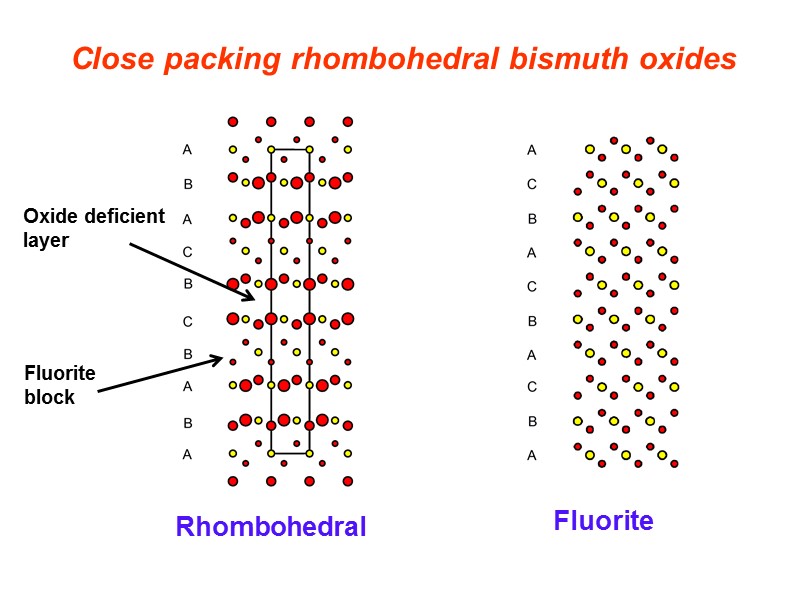
Close packing rhombohedral bismuth oxides Rhombohedral Fluorite Fluorite block Oxide deficient layer

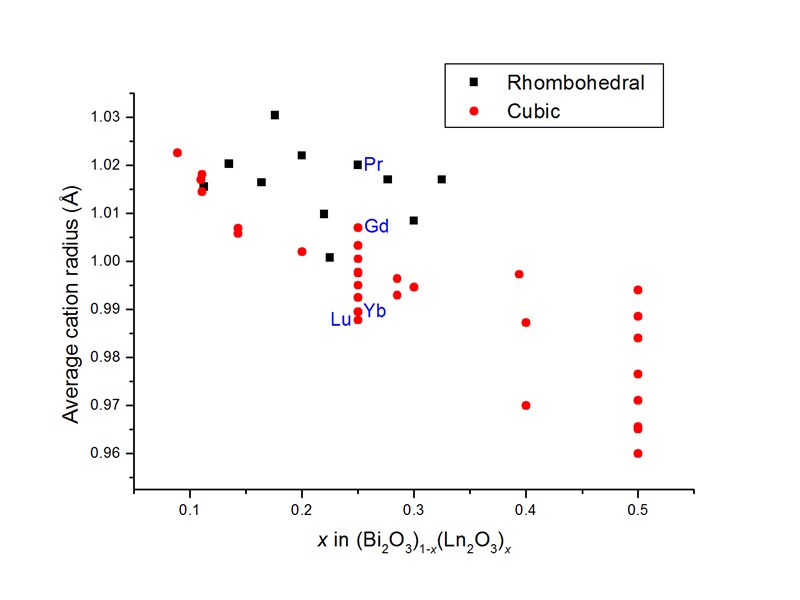
Bi3Pr1-xEuxO6 The rhombohedral phases are known to show extremely high conductivity. It has been argued by Watanabea that the fluorite phase in these systems is in fact metastable and that annealing at around 650C invariably leads to the “stable” rhombohedral phase. At the 25% level of substitution for Bi3+, the average cation radius for the Pr3+ substituted system is 1.020 Å, while that for Eu3+ substitution is 1.009 Å. Both are above that for (Gd3+ 1.007 Å) at this level of substitution, which can be viewed as the border between rhombohedral and cubic phases. Pr (4.58 fm) offers a good neutron contrast with Bi (8.532 fm).b Neutron diffraction data collected for Bi3PrO6 on Polaris. (a) A. Watanabe, Solid State Ionics, 86-88 (1996) 1427. (b) V. F. Sears, Neutron News, 3 (1992) 26.

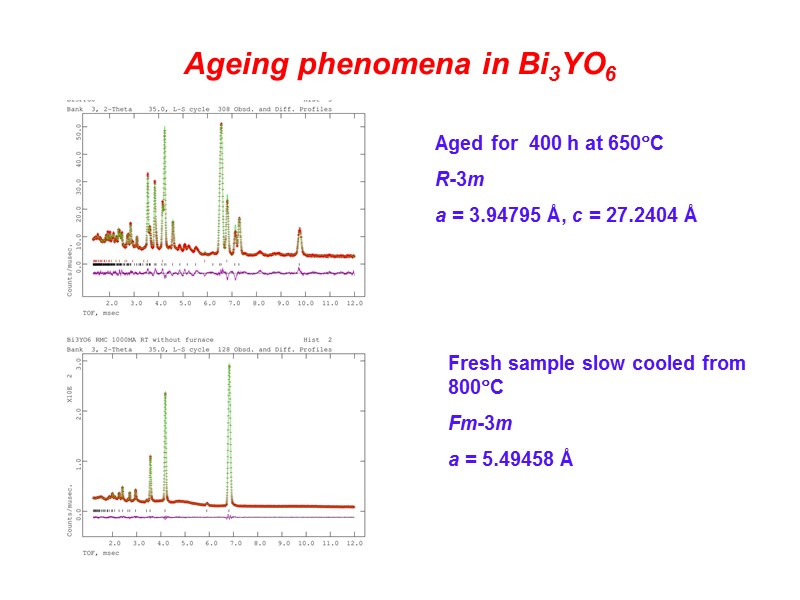
Ageing phenomena in Bi3YO6 Aged for 400 h at 650C R-3m a = 3.94795 Å, c = 27.2404 Å Fresh sample slow cooled from 800C Fm-3m a = 5.49458 Å

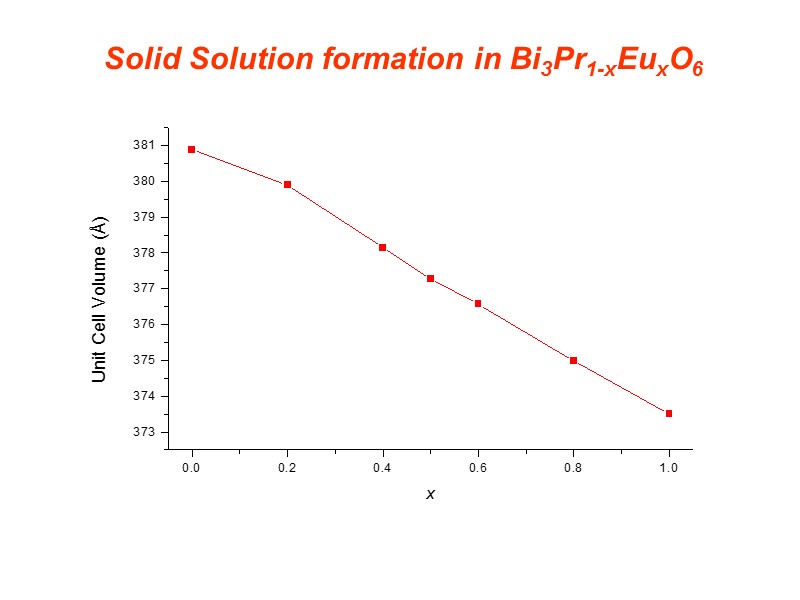
Solid Solution formation in Bi3Pr1-xEuxO6

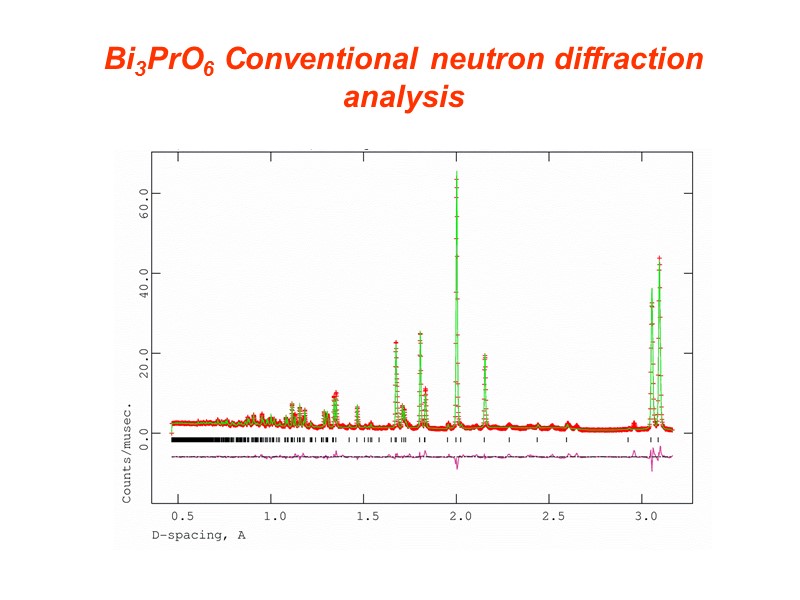
Bi3PrO6 Conventional neutron diffraction analysis

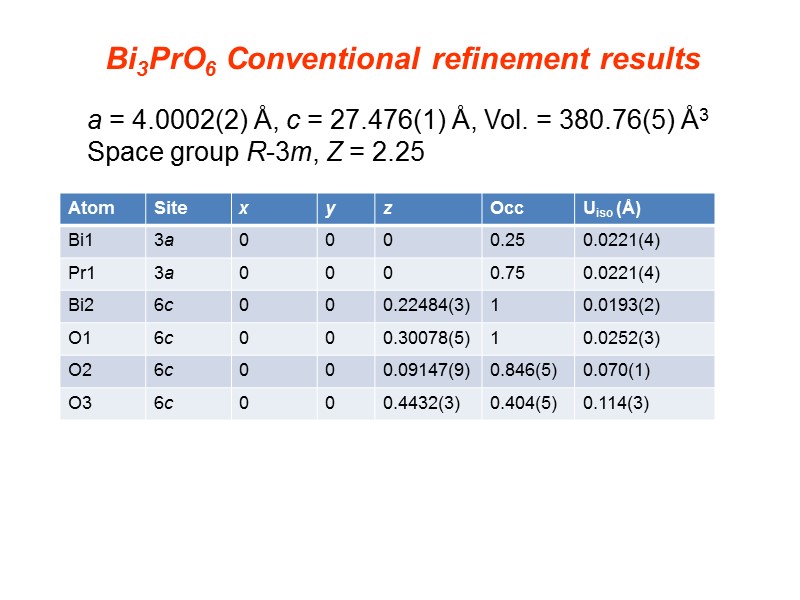
a = 4.0002(2) Å, c = 27.476(1) Å, Vol. = 380.76(5) Å3 Space group R-3m, Z = 2.25 Bi3PrO6 Conventional refinement results

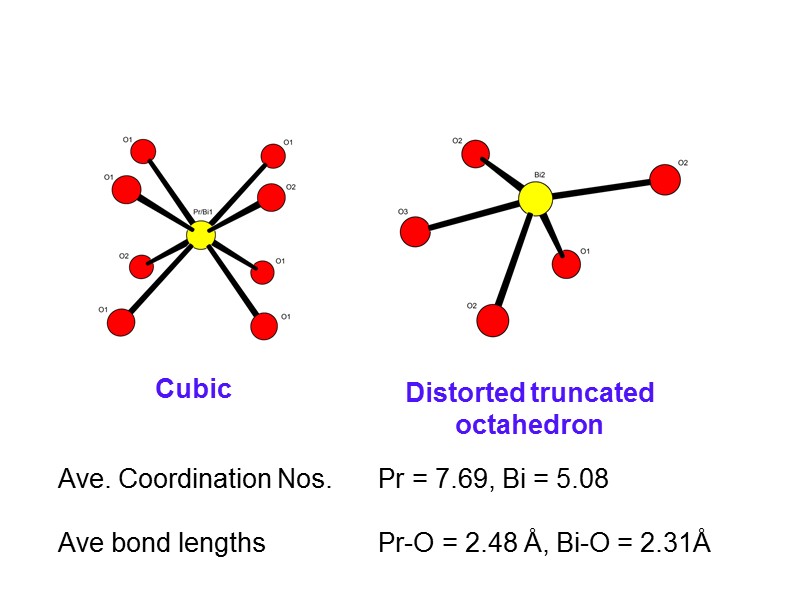
Cubic Distorted truncated octahedron Ave. Coordination Nos. Pr = 7.69, Bi = 5.08 Ave bond lengths Pr-O = 2.48 Å, Bi-O = 2.31Å

Local structure in Bi3PrO6 using a total scattering approach to structure Long range ordering in crystalline systems gives rise to sharp Bragg peaks in the powder diffraction pattern (X-ray or Neutron). Short range order manifests itself as broad background features contributing to the diffuse scattering. The total scattering approach models both the Bragg and diffuse scattering components of the diffraction pattern and gives additional information about local order. Data collected on Polaris diffractometer at ISIS Data modelled using an RMC approach (RMCProfile) using a 14 x 14 x 2 supercell (8820 atoms) in P1 symmetry.

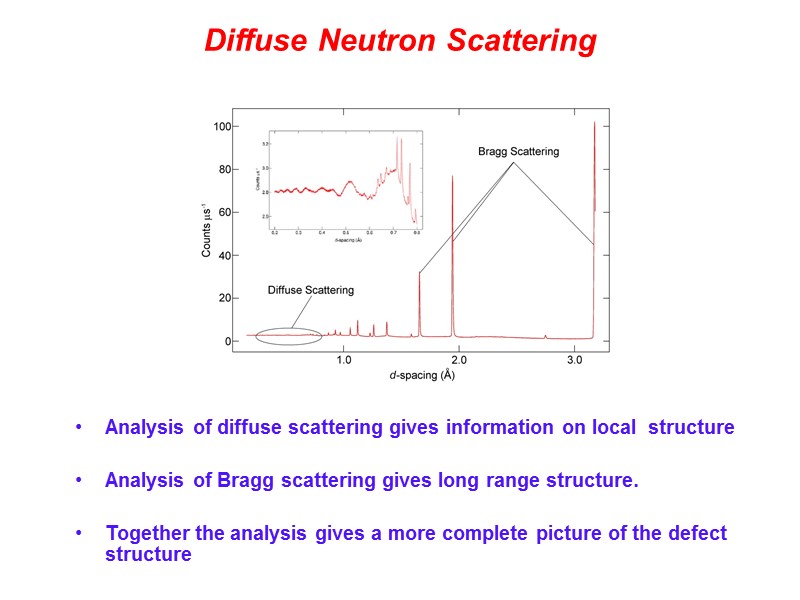
Diffuse Neutron Scattering Analysis of diffuse scattering gives information on local structure Analysis of Bragg scattering gives long range structure. Together the analysis gives a more complete picture of the defect structure

Total Scattering Key Functions F(Q) is the ‘total interference function’ i.e. total interference as a function of wave vector, Q, and contains both Bragg and diffuse scattering. As we are mostly interested in the distribution of one species () around another () we can define F(Q) as: where, S is the partial structure factor, c is the fraction of chemical species  and b is the scattering length of species , etc. G(r) The total radial distribution function, is obtained by Fourier transformation and is the sum of individual pair correlation functions (gij(r)).

The partial structure factors and pair distribution functions are therefore related by Fourier transformation.

Reverse Monte Carlo Modelling RMC is a general simulation method based on experimental data, therefore the models can be simulated without bias. The procedure is a variation of the standard Metropolis Monte Carlo simulation, and is based on the random sampling of atom positions to drive structural models to be as consistent with the experimental data as possible. The process involves an arrangement of N atoms (the configuration) that are generated within certain ranges in a three-dimensional box. Some of the atoms are selected randomly and moved a random amount, under periodic boundary conditions. Each time, the difference (usually of the structure factors) between the new model and the data are recalculated, and the difference minimizing movements are accepted. Most but not all of the other movements are rejected.

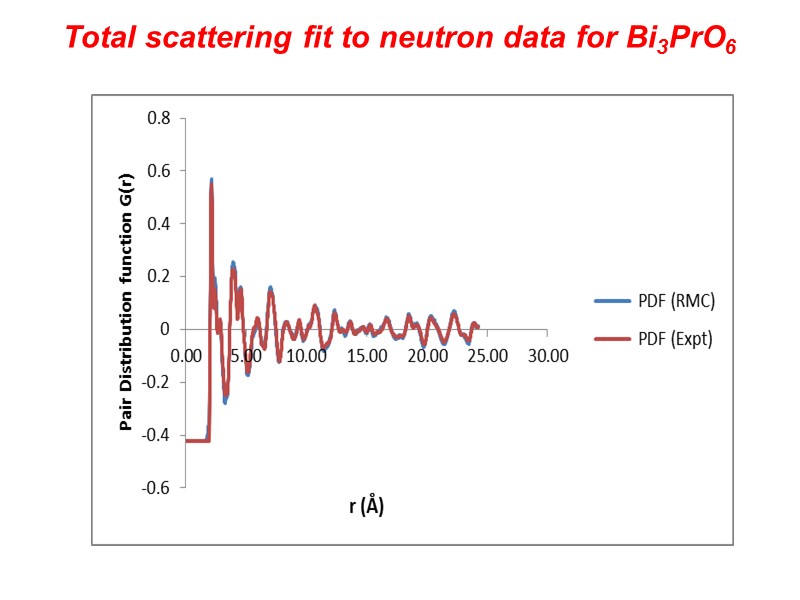
Total scattering fit to neutron data for Bi3PrO6

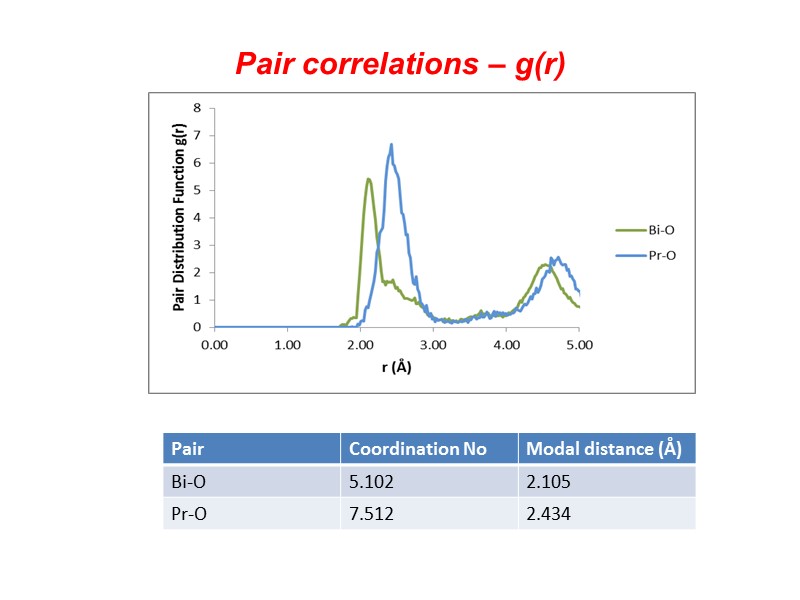
Pair correlations – g(r)

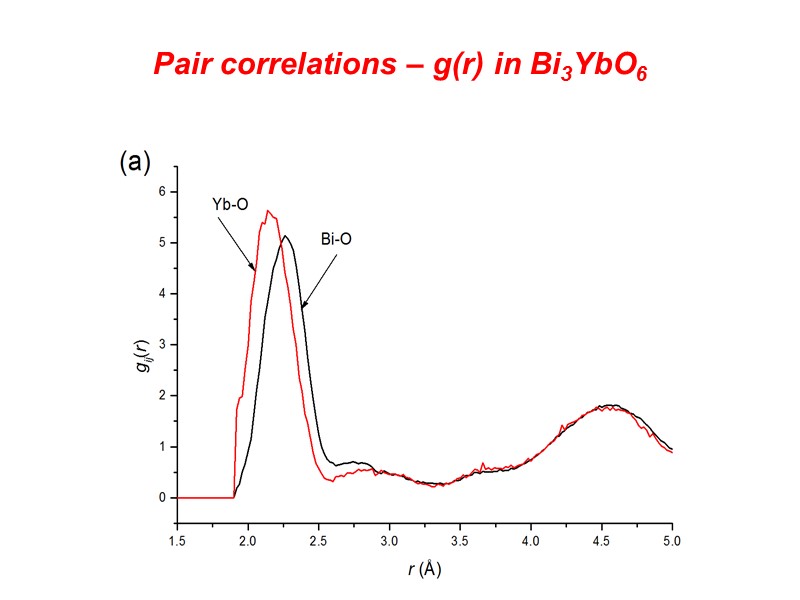
Pair correlations – g(r) in Bi3YbO6

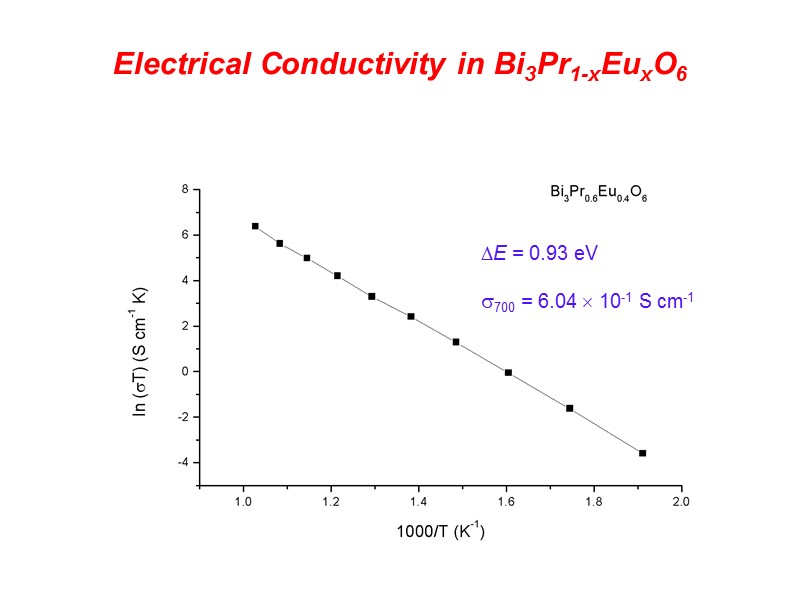
Electrical Conductivity in Bi3Pr1-xEuxO6 E = 0.93 eV 700 = 6.04  10-1 S cm-1

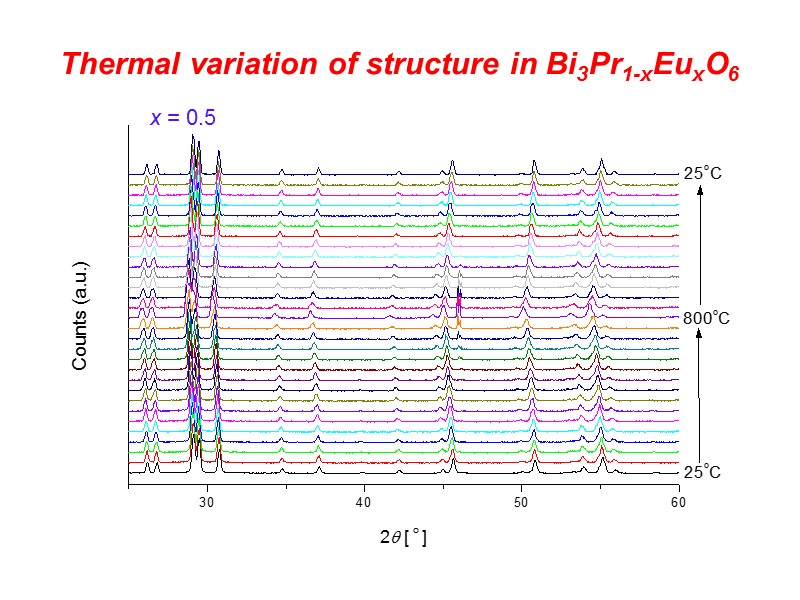
Thermal variation of structure in Bi3Pr1-xEuxO6 x = 0.5

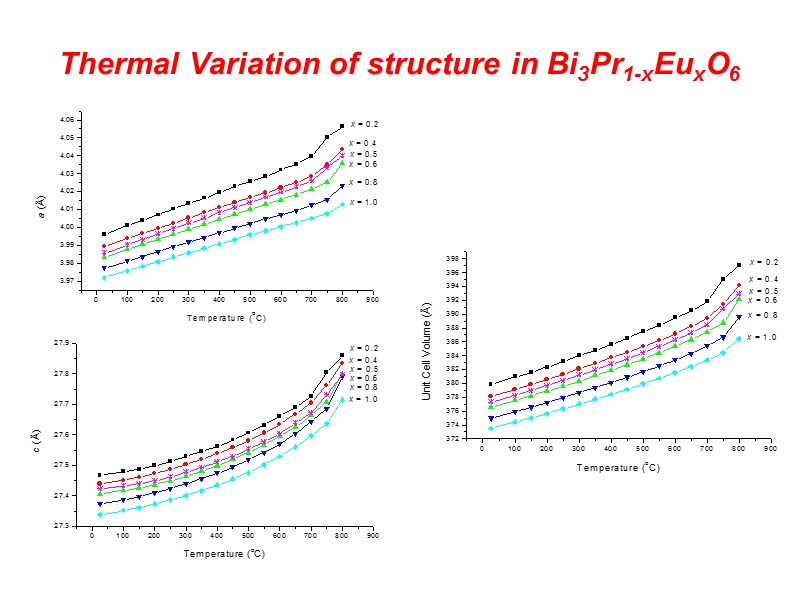
Thermal Variation of structure in Bi3Pr1-xEuxO6

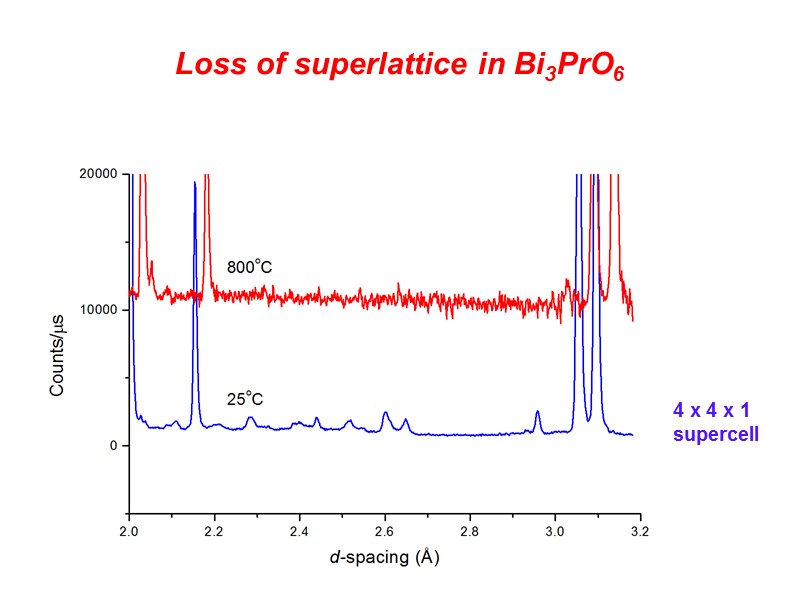
Loss of superlattice in Bi3PrO6 4 x 4 x 1 supercell

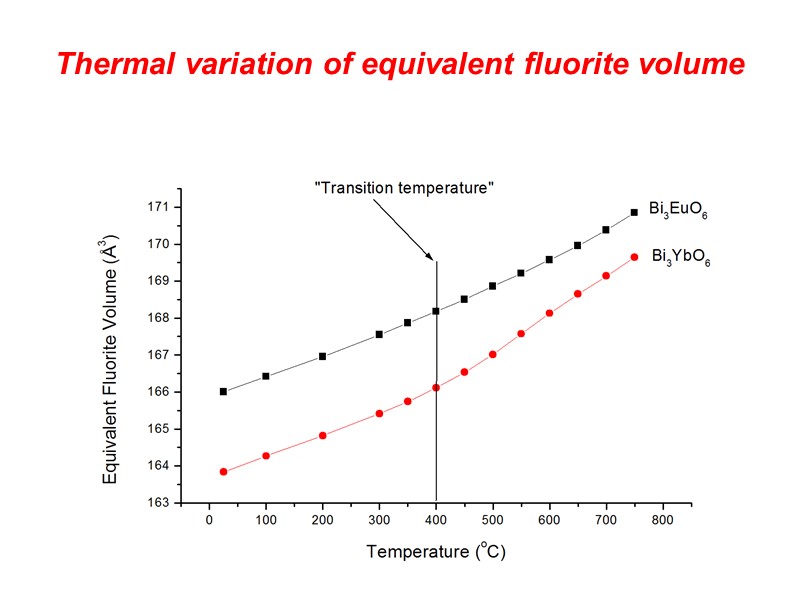
Thermal variation of equivalent fluorite volume

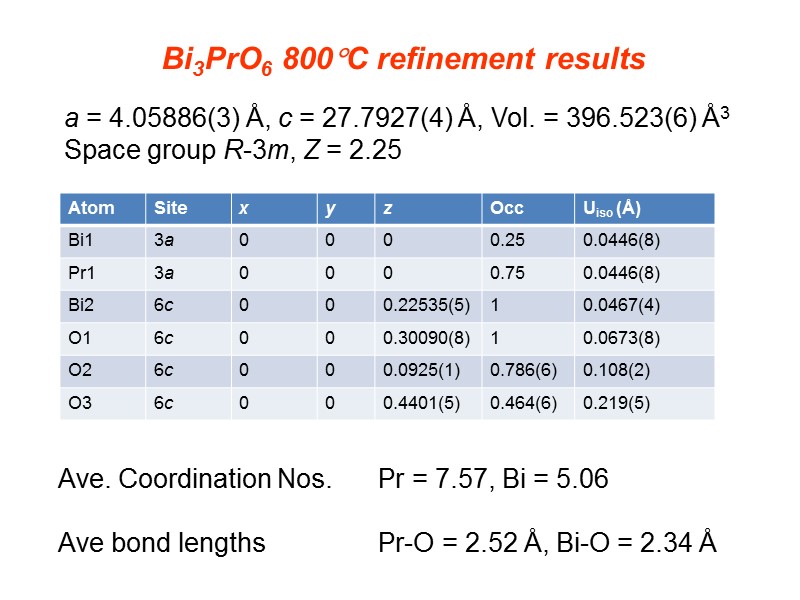
a = 4.05886(3) Å, c = 27.7927(4) Å, Vol. = 396.523(6) Å3 Space group R-3m, Z = 2.25 Bi3PrO6 800C refinement results Ave. Coordination Nos. Pr = 7.57, Bi = 5.06 Ave bond lengths Pr-O = 2.52 Å, Bi-O = 2.34 Å

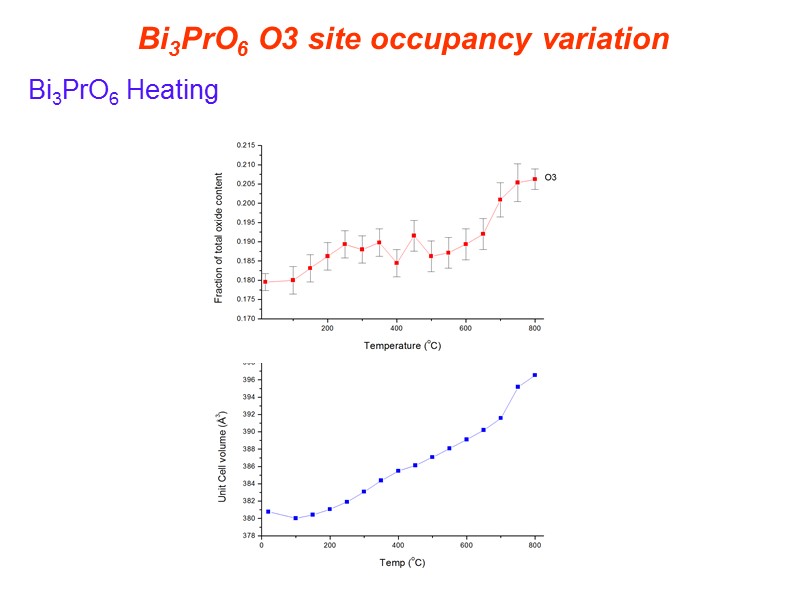
Bi3PrO6 Heating Bi3PrO6 O3 site occupancy variation

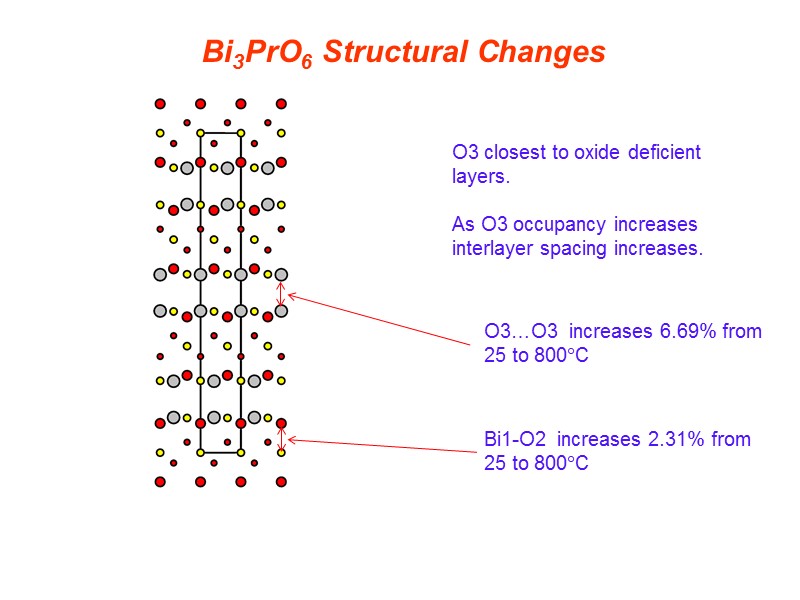
O3 closest to oxide deficient layers. As O3 occupancy increases interlayer spacing increases. O3…O3 increases 6.69% from 25 to 800C Bi1-O2 increases 2.31% from 25 to 800C Bi3PrO6 Structural Changes

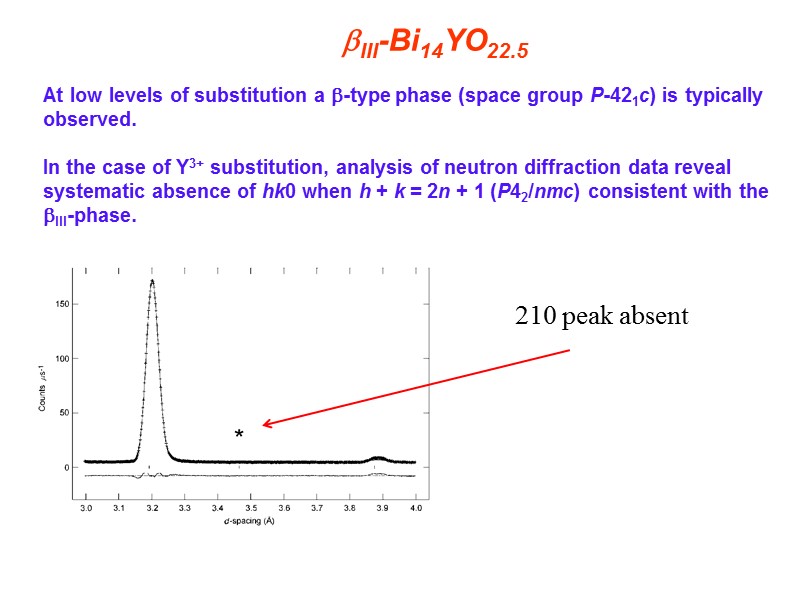
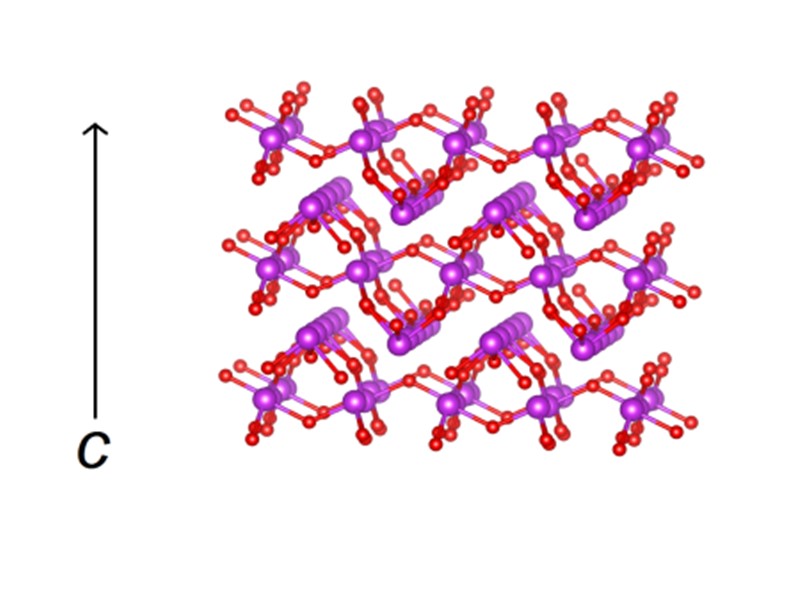
III-Bi14YO22.5 At low levels of substitution a -type phase (space group P-421c) is typically observed. In the case of Y3+ substitution, analysis of neutron diffraction data reveal systematic absence of hk0 when h + k = 2n + 1 (P42/nmc) consistent with the III-phase. 210 peak absent

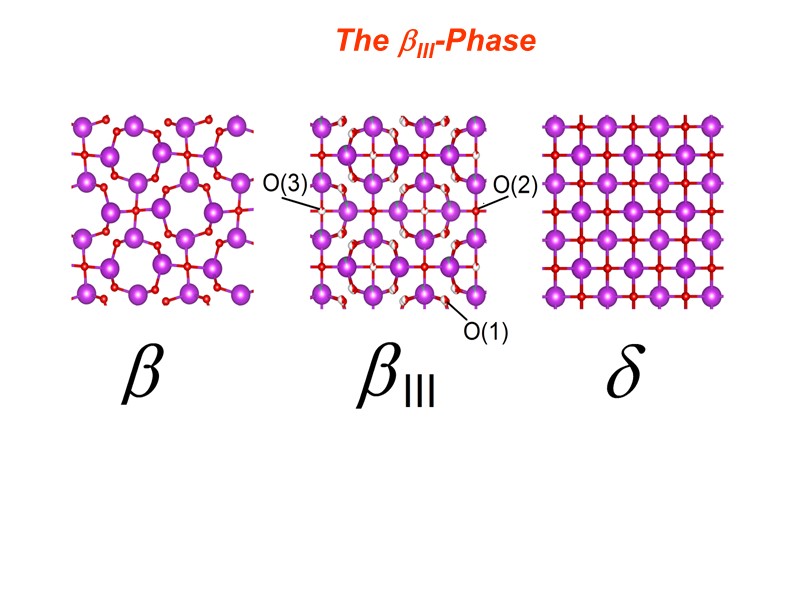
The III-Phase

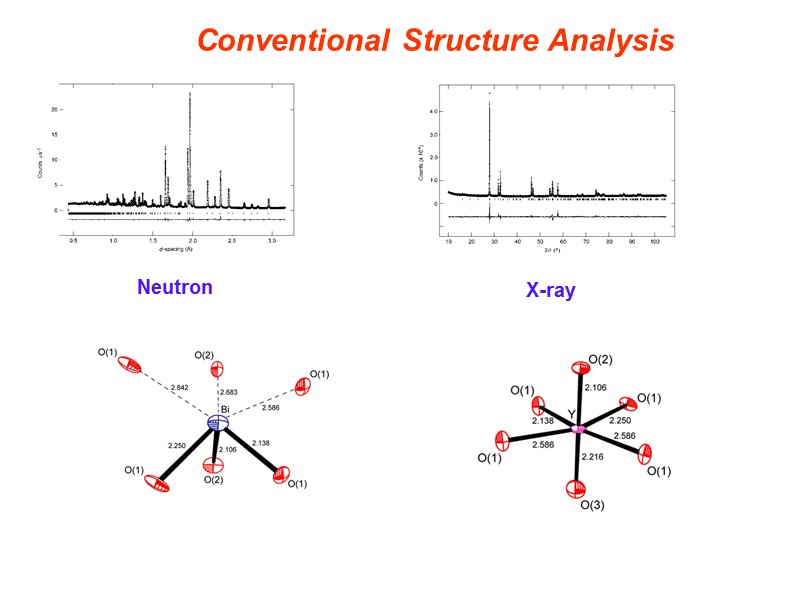
Conventional Structure Analysis X-ray Neutron

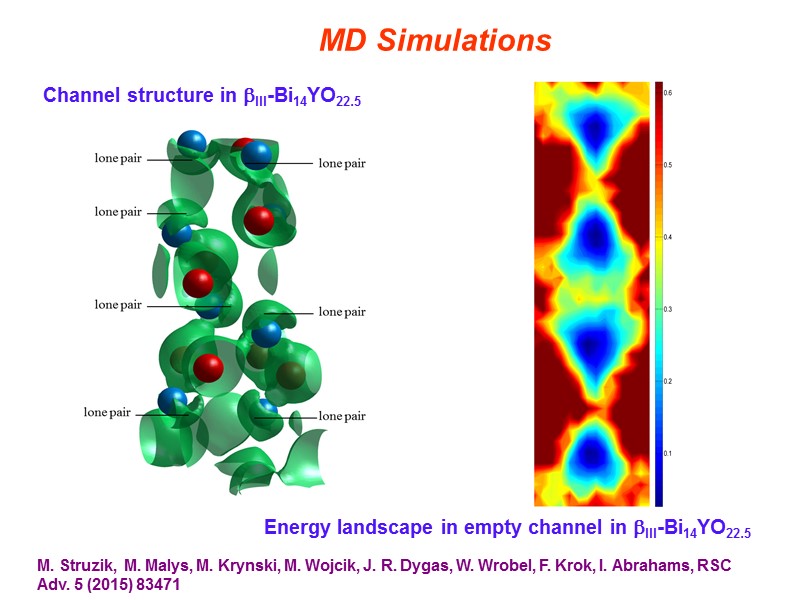
MD Simulations Channel structure in III-Bi14YO22.5 Energy landscape in empty channel in III-Bi14YO22.5 M. Struzik, M. Malys, M. Krynski, M. Wojcik, J. R. Dygas, W. Wrobel, F. Krok, I. Abrahams, RSC Adv. 5 (2015) 83471

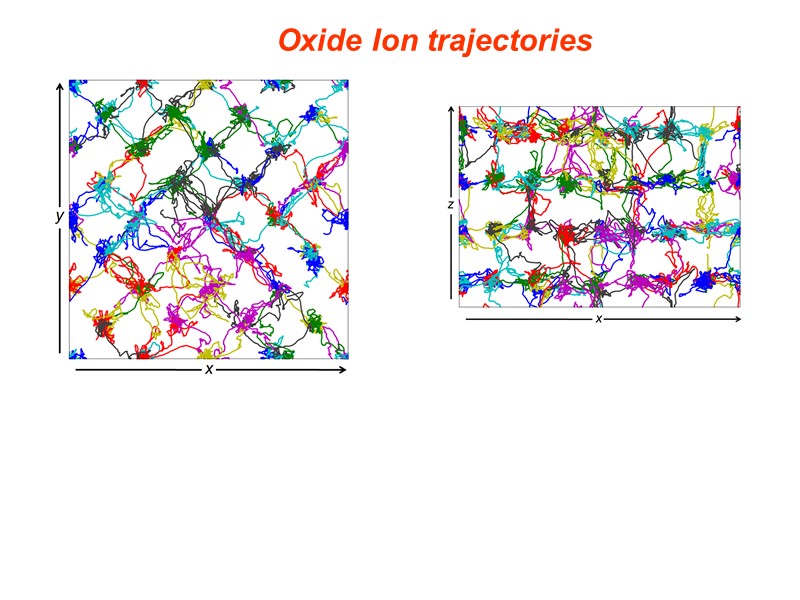
Oxide Ion trajectories

Conclusions At the local level structures are adopted that satisfy the preferred coordination geometry of Bi and of the substituent cation. Superlattice ordering of the fluorite structure is evident in supervalent cation substituted systems including both commensurate and incommensurate modulations. Clustering of dopant polyhedra is evident leading to chain formation. In isovalent substituted systems, phases related to the fluorite phase are observed. In the rhombohedral phase the thermal variation of lattice parameters reveals significant curvature in the c-axis contraction on cooling. This is reflected by an apparent change in slope in the volume contraction at about 600C. This appears to be correlated with a continuous change in the oxide ion distribution, resulting in changes in the interlayer spacing. Similar phenomena may occur in other substituted bismuth oxides. MD Simulations reveal that ionic conduction in the III-phase appears to be 3-dimensional rather than 1-dimensional, despite the presence of a channel structure.