1a48ebf2ba67417f9ab836495e08fcca.ppt
- Количество слайдов: 18

A Statistical Model of Criminal Behavior M. B. Short, M. R. D’Orsogna, V. B. Pasour, G. E. Tita, P. J. Brantingham, A. L. Bertozzi, L. B. Chayez Maria Pavlovskaia

Goal • Model the behavior of crime hotspots • Focus on house burglaries

Assumptions • Criminals prowl close to home • Repeat and near-repeat victimization

The Discrete Model • A neighborhood is a 2 d lattice • Houses are vertices • Vertices have attractiveness values Ai • Criminals move around the lattice

Criminal Movement A criminal can: • Rob the house he is at - or • Move to an adjacent house • Criminals regenerate at each node

Criminal Movement • Modeled as a biased random walk

Attractiveness Values • Rate of burglary when a criminal is at that house • Has a static and a dynamic component • Static (A 0) - overall attractiveness of the house • Dynamic (B(t)) - based on repeat and near-repeat victimization

Dynamic Component • When a house s is robbed, Bs(t) increases • When a neighboring house s’ is robbed, Bs(t) increases • Bs(t) decays in time if no robberies occur

Dynamic Component • The importance of neighboring effects: • The importance of repeat victimization: • When repeat victimization is most likely to occur: • Number of burglaries between t and t: Es(t)
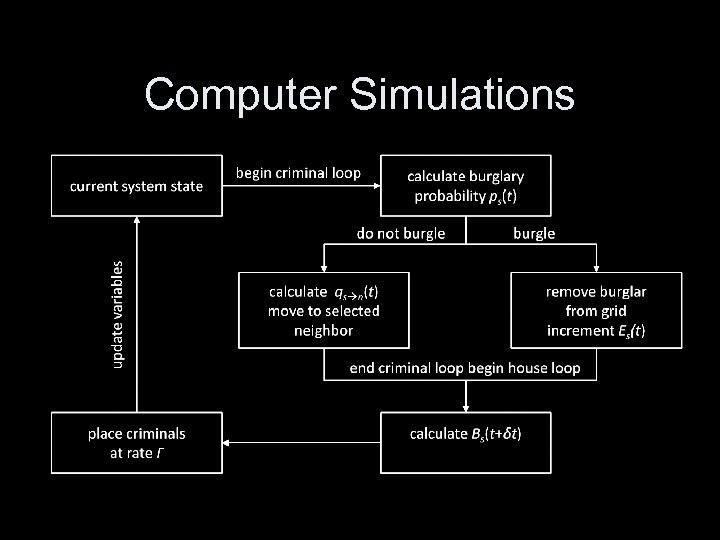
Computer Simulations

Computer Simulations Three Behavioral Regimes are Observed: • Spatial Homogeneity • Dynamic Hotspots • Stationary Hotspots
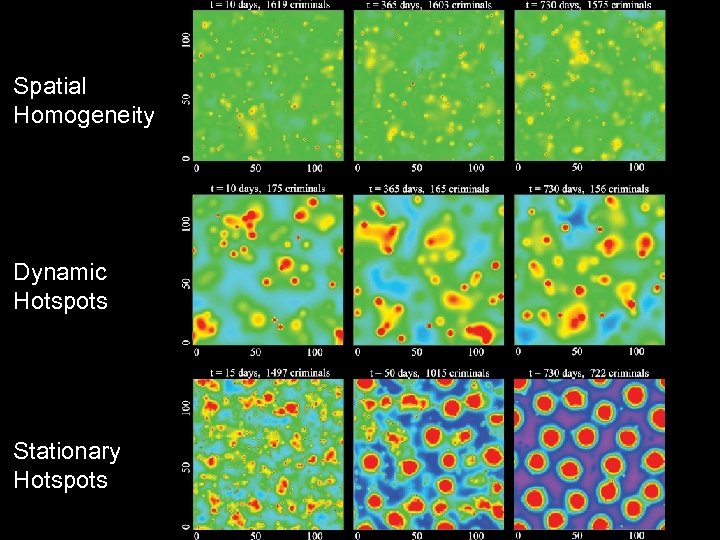
Spatial Homogeneity Dynamic Hotspots Stationary Hotspots

Computer Simulations Three Behavioral Regimes are Observed: • Spatial Homogeneity – Large number of criminals or burglaries • Dynamic Hotspots – Low number of criminals and burglaries – Manifestation of the other two regimes due to finite size effects • Stationary Hotspots – Large number of criminals or burglaries

Continuum Limit In the limit as the time unit and the lattice spacing becomes small: • The dynamic component of attractiveness: • The criminal density:

Continuum Limit • Reaction-diffusion system • Dimensionless version is similar to: – Chemotaxis models in biology (do not contain the time derivative) – Population bioglogy studies of wolfe and coyote territories

Computer Simulations • Dynamic Hotspots are never seen • Spatial Homogeneity or Stationary Hotspots? – Performed linear stability analysis – Found an inequality to distinguish between the cases

Summary • Discrete Model • Computer Simulations – Spatial Homogeneity, Dynamic Hotspots, Stationary Hotspots • Continuum Limit – Dynamic Hotspots are not observed: due to finite size effects – Inequality to distinguish between Homogeneity and Hotspots cases

Applications • House burglaries • Assault with a lethal weapon • Muggings • Terrorist attacks in Iraq • Lootings
1a48ebf2ba67417f9ab836495e08fcca.ppt