A Simple Model of Aeolian Megaripples Hezi Yizhaq

A Simple Model of Aeolian Megaripples Hezi Yizhaq 1, Antonello Provenzale 2 and Neil J. Balmforth 3 1 BIDR, 2 CNR-ISAC, Ben-Gurion University, Israel Torino, Italy, CIMA; University of Genoa, Italy 3 UCSC, Santa Cruz, CA, USA Email: yiyeh@bgumail. bgu. ac. il 1

Megaripples gallery Death Valley Nahal Kasui, Negev, Israel Peru

Talk’s Outline 1. Ripples and megaripples characteristics 2. Sand transport mechanisms 3. Mathematical model of normal sand ripples 4. Mathematical model of megaripples 5. Conclusions and suggestions for future reserch

stoss lee cross section h Normal Ripples Wavelength 10 -25 cm Megaripples >25 cm up to 20 m 1 to 4 mm Grain size Time scale Journal of Geology, 1981, 89, 129 0. 06 to 0. 5 mm minutes Sorting Unimodal Bimodal distribution days, weeks

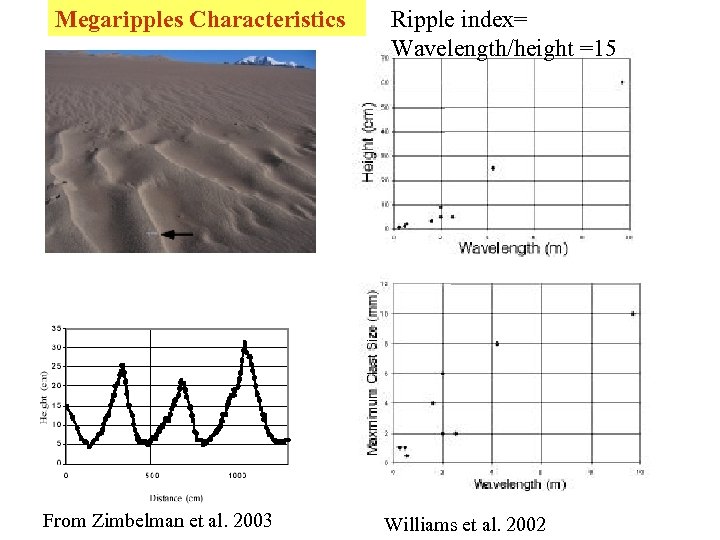Megaripples Characteristics From Zimbelman et al. 2003 Ripple index= Wavelength/height =15 Williams et al. 2002

Megaripples on Mars wind Sand dunes and ripple patterns in Kaiser Crater. The picture shows an area about 1. 9 miles (3 km) wide and is sunlit from the upper left. 3 km Image Credit: NASA/JPL/Malin Space Science Systems l~12 m l~13 m Aeolian activity on Mars was first mentioned in 1909 by E. M Antoniadi.

Sand Transport by the wind Saltation: high-energy population of grains in motion. Reptation: low-energy population of grains in motion.

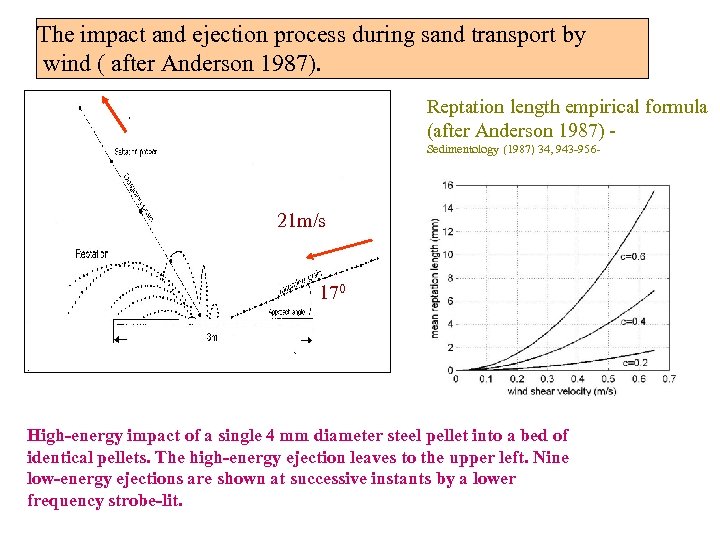The impact and ejection process during sand transport by wind ( after Anderson 1987). Reptation length empirical formula (after Anderson 1987) Sedimentology (1987) 34, 943 -956 - 21 m/s 170 High-energy impact of a single 4 mm diameter steel pellet into a bed of identical pellets. The high-energy ejection leaves to the upper left. Nine low-energy ejections are shown at successive instants by a lower frequency strobe-lit.

Anderson’s model: Eolian sand ripples as a selforganization phenomenon. Sedimentology, 34 (1987) 943; Earth-Science Reviews, 29 (1990) 77 -96 Simplifications: 1. The saltation population is uniform in space. 2. (i. e. it will not include in the model) 3. 2. All saltating grains impact an horizontal surface with an identical angle (between 100 and 150). 4. 3. The granular bed is composed of identical grains.

A model for normal sand ripples Approximation: is spatially constant

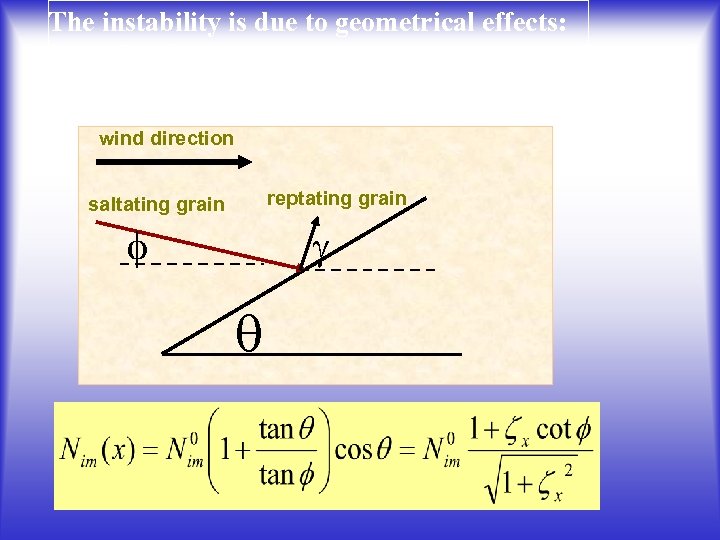The instability is due to geometrical effects: an inclined surface is subject to more abundant collisions than a flat one. wind direction reptating grain saltating grain f g q

Reptation flux on flat surface : Our new assumption: The reptation flux depends on the bed slope, such it is decreased on the stoss slope and incresed on the lee slope, mathematically: Ballistic effect Rolling effect Bed slope

The integro-differential equation: Local shadowing effect: Yizhaq et al. submitted to Physica D.

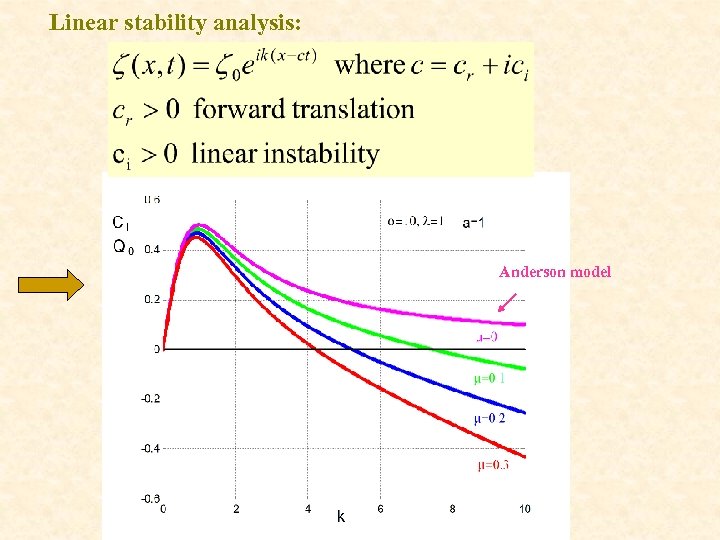Linear stability analysis: Anderson model

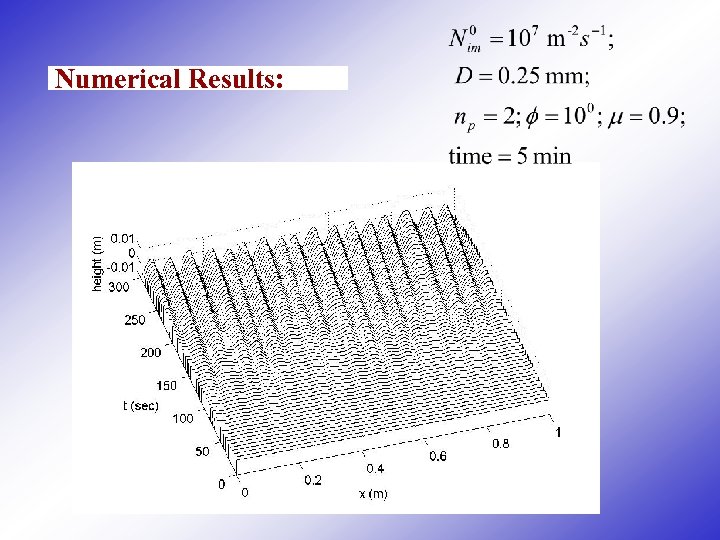Numerical Results:

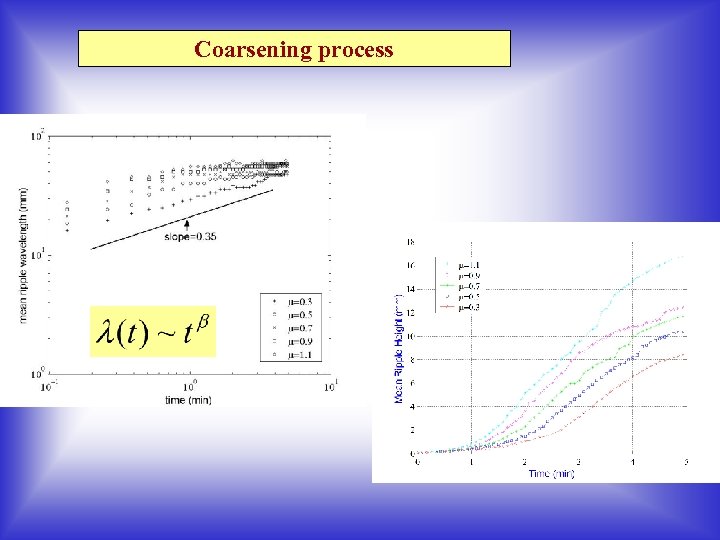Coarsening process

Long-Wave Approximation Goal: Getting a PDE nonlinear equation for the dynamics of sand ripples near the instability onset from the integro-differential equation. A compact description of the dynamics. I. Nondimensional Variables: II. Near the instability onset: III. Taylor series expansion of IV. Assuming m~e and T=e 2 t; define: and we add sand transport in the lateral direction…

Two Dimensional Ripples: long-wave expansion equation We assume pure rolling in the transverse direction The model: *Animations were done with the help of Jost von Hardenberg. (CNR-ISAC) z wind y x

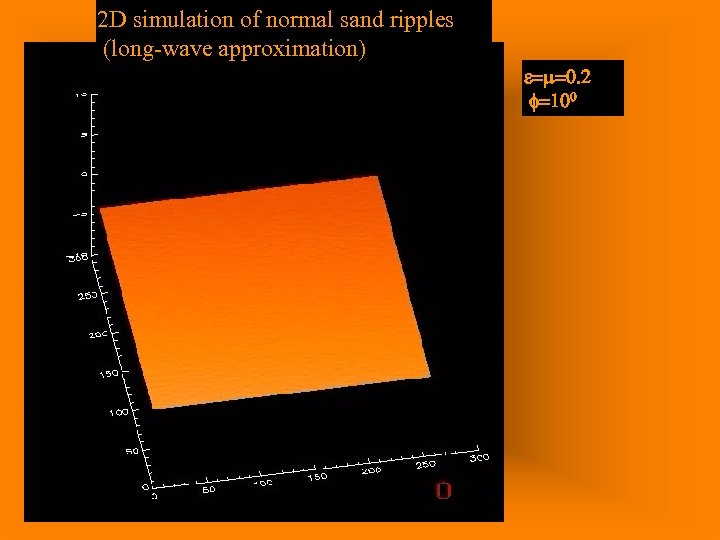2 D simulation of normal sand ripples (long-wave approximation) e=m=0. 2 f=100

A Mathematical Model for Megaripples Bagnold (1941) necessary conditions for megaripples formation: 1. Availability of sufficient coarse grains. 2. A constant supply of fine sand in saltation to sustain forward movement of coarse grains. 3. Wind velocity below the threshold to remove coarse grains from the megaripples crest. Fine-fraction impact ripples (Elwood et al. 1975) Fine particles saltation Coarse particles reptation Mean saltation length can be very large for fine particles which rebound from coarse grained surface and for strong winds. (up to 20 m)

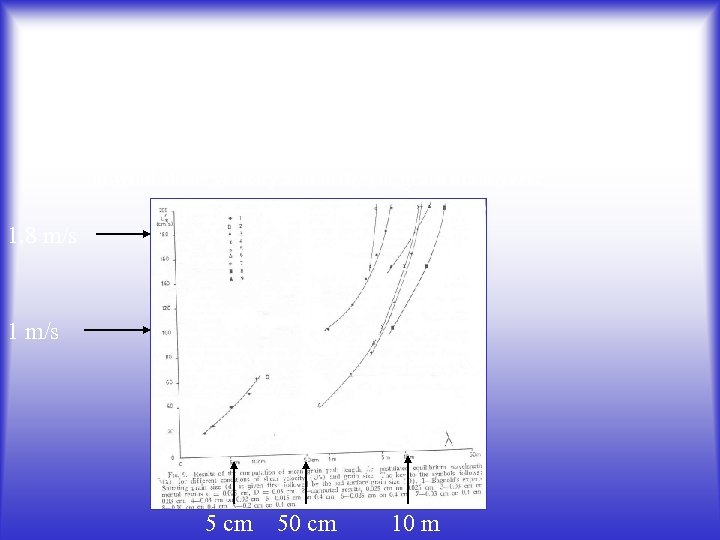Extension of Bagnold’s idea by Ellwood et al. (1975) The mean saltation length can explain also the formation megaripples which developed in bimodal sands. They calculated the mean saltation path for different values of wind shear velocity and different grain diameters. 1. 8 m/s 1 m/s 5 cm 50 cm 10 m

Integro-differential equation for 1 D megaripples Sand flux =saltation flux of fine grains +reptation flux of coarse grains crest close-up

Exner equation: e ratio between coarse grains to fine grains at the surface e=0 unimodal fine sand e=1 equally distribution of fine and coarse grains

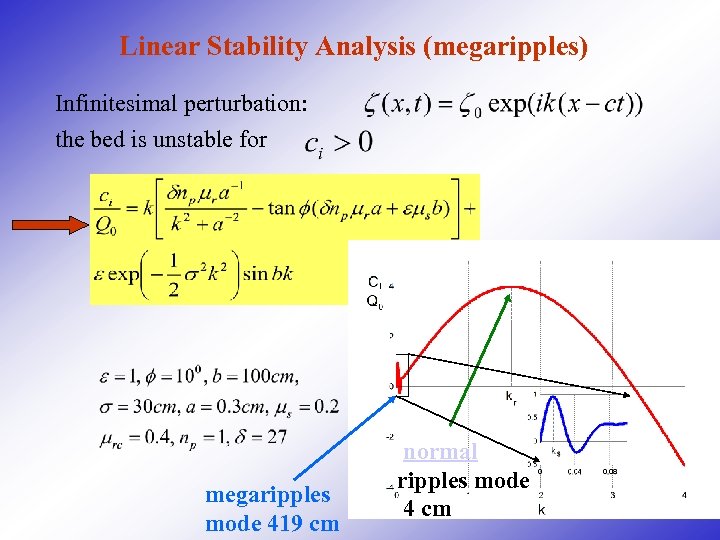Linear Stability Analysis (megaripples) Infinitesimal perturbation: the bed is unstable for megaripples mode 419 cm normal ripples mode 4 cm

wind megaripples normal ripples Megaripples formed in a patch of coarse sand.

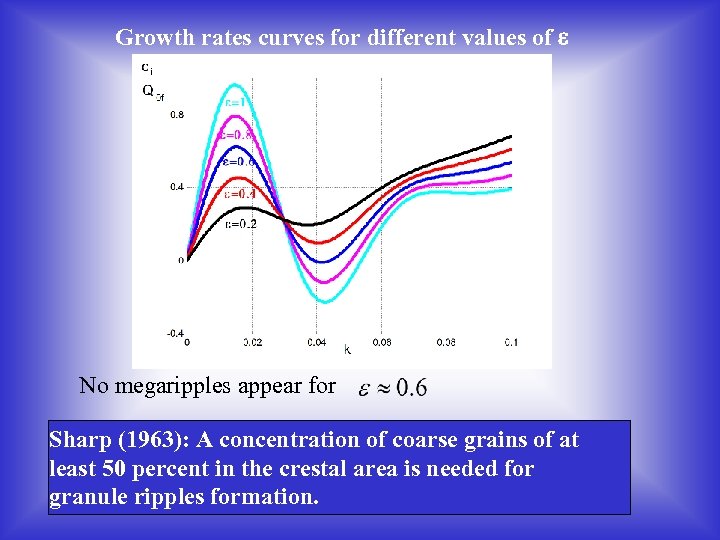Growth rates curves for different values of e No megaripples appear for Sharp (1963): A concentration of coarse grains of at least 50 percent in the crestal area is needed for granule ripples formation.

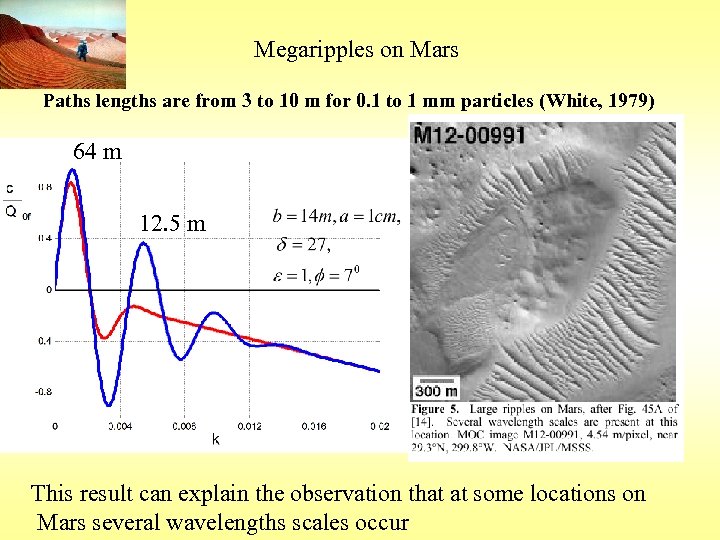Megaripples on Mars Paths lengths are from 3 to 10 m for 0. 1 to 1 mm particles (White, 1979) 64 m 12. 5 m This result can explain the observation that at some locations on Mars several wavelengths scales occur

Conclusions and suggestions for future studies 1. The proposed mathematical model takes into account both saltation flux of fine particles and reptation flux of coarse particles and can explain various field observations. 2. Linear stability analysis indicates that the megaripples wavelength is about 4 times the mean saltation length of fine grains. 3. Numerical simulations of the integro-differential equation are needed in order to find megaripple evolution and profiles. 4. Careful experimental work is needed in order to estimate the values of the model’s parameters.

The