A Practical and Precise Inference and Specializer for

A Practical and Precise Inference and Specializer for Array Bound Checks Elimination Corneliu Popeea Natl Univ of Singapore Dana N. Xu Univ of Cambridge Wei-Ngan Chin Natl Univ of Singapore PEPM 2008 - 8 January 1

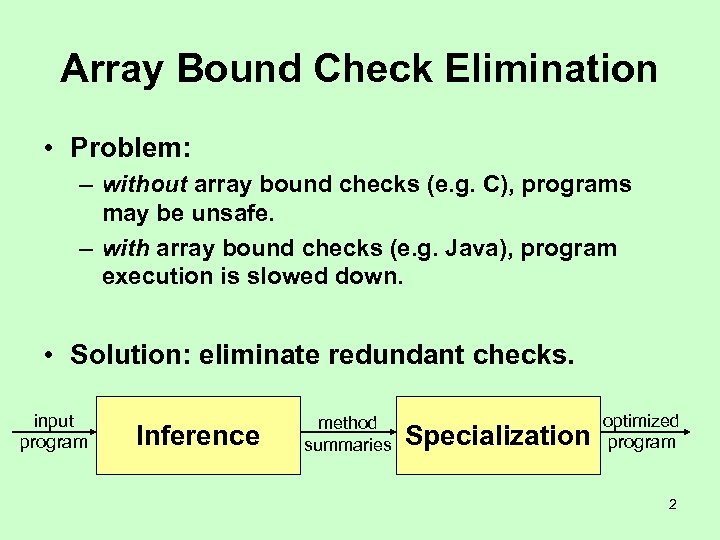Array Bound Check Elimination • Problem: – without array bound checks (e. g. C), programs may be unsafe. – with array bound checks (e. g. Java), program execution is slowed down. • Solution: eliminate redundant checks. input program Inference method summaries Specialization optimized program 2

Inference Goal: derive preconditions that make checks redundant. float foo (float a[], int j, int n) { float v=0; int i = j+1; L 1 if (0=0 Our contributions: modular inference of preconditions. handling indirection arrays. 3

Specialization Goal: eliminate runtime checks guided by inference results. • If we assume all callers satisfy (j+1< len(a)) : float foo (float a[], int j, int n) { float v = 0; int i = j+1; L 1 if (0

Overview • Introduction • Our approach – Modular inference: postcondition + preconditions. – Flexi-variant specialization. • Experimental results. • Conclusion. 5

Setting • First order imperative language: meth : : = t mn ( ([ref] t v)* ) { e } t : : = int | float | t[int, . . , int] e : : = k | v | if v then e 1 else e 2 | v=e | t v=e 1; e 2 | mn(v*) - method - type - expression • Invariants expressed as linear formulae: Q : : = { q(v*) = Á } Á : : = Á1ÆÁ2| Á1ÇÁ2| q(v*) | s s : : = a 1 v 1 +. . + anvn · a - recursive formula - linear inequality 6

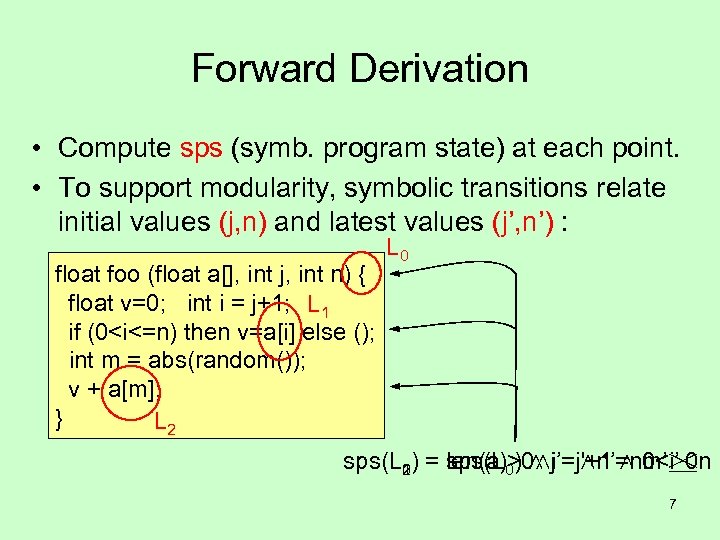Forward Derivation • Compute sps (symb. program state) at each point. • To support modularity, symbolic transitions relate initial values (j, n) and latest values (j’, n’) : float foo (float a[], int j, int n) { float v=0; int i = j+1; L 1 if (00Æj’=jÆn’=nm’¸ 0 0 2 7

Forward Derivation for Recursion • Each method is first translated to a recursive constraint. • Compute an over-approximation of the least fixed point of this recursive constraint: – precise disjunctive polyhedron abstract domain. – with hulling and widening operators. • Details and examples in the paper. 8

Indirection Arrays • Hold indexes for accessing another array. • Used intensively for sparse matrix operations. • Need to capture universal properties about elements inside array: 8 i 2 indexes(a) ¢ 0 · a[i] · 10 represented as: 0 · a_elem · 10 9

Indirection Arrays • Given method: void init. Arr(int a[], int i, int j, int n) { if (i>j) then () else { a[i]=n; init. Arr(a, i+1, j, n+1) } • Compute postcondition: (i>j Æ a_elem'=a_elem) Ç (0·i·j

Inference of Preconditions • Classify checks with pre = 8 L¢(sps ) chk) – pre is valid: safe check. – pre is unsatisfiable: unsafe check. –. . otherwise propagate pre as a check for the caller. 11

Example: Preconditions • Derive weakest precondition for each check: float foo (float a[], int j, int n) { float v = 0; int i = j+1; L 1 if (00 Æ i'=j'+1 Æ 0

Efficient Preconditions • Problem: negation of sps results in large preconditions. – naïve pre-derivation: (len(a)· 0) Ç (j

Inference Result: Method Summary float foo (float a[], int j, int n) { float v = 0; int i = j+1; L 1 if (0

Overview • Introduction • Our approach – Modular inference: postcondition + preconditions. – Flexi-variant specialization. • Experimental results. • Conclusion. 15

Specialization • If we assume all contexts satisfy (j+1 < len(a)): float foo (float a[], int j, int n) { float v = 0; int i = j+1; L 1 if (0

Specialization • Monovariant specializer – One specialized code for each method. – Lower bound of all optimization. – Compact code size. • Polyvariant specializer – Multiple optimized codes per method. – Each call site is replaced by a specialized call. – Highly optimized but may have code blow-up. 17

Flexivariant Specialization • Allows trade-off between optimization and code size. • Decides how many copies to generate per method, based on frequency and size constraint. • Less optimization - 1 copy: • More optimization - 2 copies: foo (2 runtime checks). foo 1 (1 runtime check) + foo 2 (2 runtime checks) 18

Soundness • Inference + Specialization = Well-typed program Theorem: Given a program P and an inference judgment ` P PI. Let Bflex PI PT be the specialization of PI to PT. Then, if PT is well-typed, its execution will never proceed to invalid array-accesses. 19

Implementation • Prototype written in Haskell language: – uses an efficient Presburger solver [W. Pugh et al]. – disjunctive fixed-point analyzer [Popeea and Chin]. • Test programs: – small programs: binary search, merge sort, quick sort. – numerical benchmarks: Fast Fourier Transform, LU decomposition, Linpack. 20

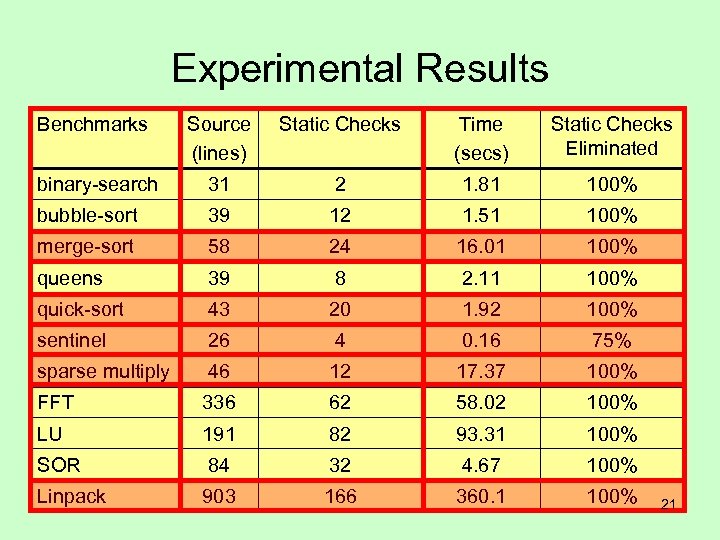Experimental Results Benchmarks Source (lines) Static Checks Time (secs) Static Checks Eliminated binary-search 31 2 1. 81 100% bubble-sort 39 12 1. 51 100% merge-sort 58 24 16. 01 100% queens 39 8 2. 11 100% quick-sort 43 20 1. 92 100% sentinel 26 4 0. 16 75% sparse multiply 46 12 17. 37 100% FFT 336 62 58. 02 100% LU 191 82 93. 31 100% SOR 84 32 4. 67 100% Linpack 903 166 360. 1 100% 21

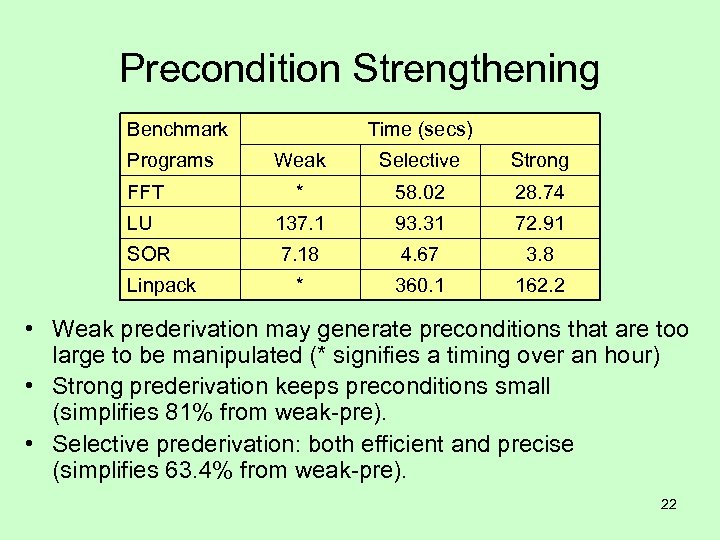Precondition Strengthening Benchmark Programs Time (secs) Weak Selective Strong FFT * 58. 02 28. 74 LU 137. 1 93. 31 72. 91 SOR 7. 18 4. 67 3. 8 * 360. 1 162. 2 Linpack • Weak prederivation may generate preconditions that are too large to be manipulated (* signifies a timing over an hour) • Strong prederivation keeps preconditions small (simplifies 81% from weak-pre). • Selective prederivation: both efficient and precise (simplifies 63. 4% from weak-pre). 22

Conclusion • Modular summary-based analysis: – Disjunctive postcondition inference – Derivation of efficient, scalable preconditions. • Integration with a flexi-variant specializer. • Implementation of a prototype system. • Correctness proof. 23

A Practical and Precise Inference and Specializer for Array Bound Checks Elimination Corneliu Popeea, Dana N. Xu, Wei-Ngan Chin We thank Siau-Cheng Khoo for sound and insightful suggestions. Thanks to anonymous referees for comments. 24

Related Work • Global analyses: – Techniques: Suzuki and Ishihata [POPL'77], Cousot and Halbwachs [POPL'78] – Tools: Astreé [PLDI'03], C Global Surveyor [PLDI'04] • Modular analyses: – Cousot and Cousot [IFIP'77, CC'02] – Chatterjee, Ryder and Landi [POPL'99] – Moy [VMCAI'08] • Dependent type checking: – Xi and Pfenning [PLDI'98] 25

• Limitations: – Large formulae: currently under-approx. formulae are propagated. Over-approx. formulae are more compact, since sps appears in a positive position. • Future work: – Dual analysis to validate some alarms as true bugs. – Extend the analysis with sound treatment of reference types. – Handle more (existential) properties about array elements. 26

Two Kinds of Recursive Invariants • For loops: – compute a loop invariant. • For methods with general recursion: – compute a loop invariant. – the method postcondition cannot be determined directly from the loop invariant: a separate fixed-point is computed. 27

VCgen Verification Condition Generator • Backward VCgen: – given: {P} assert chk {Q} – derives: P = (Q Æ chk) • Our precondition derivation: – given: {pre} …; assert chk {sps} – derives: pre = (sps => chk) • Differences: – sps is a transition relation: pre holds at the beginning of the current method. – sps is computed by a separate forward derivation. 28