A Novel Method for Determining the Mean-Field Directly

A Novel Method for Determining the Mean-Field Directly From the Single Particle Matter Density Shalom Shlomo Texas A&M University Collaborators: Mason Anders Igal Talmi

Outline 1. Introduction 2. Derivation of method, mean field from matter density 3. Application to 3 s 1/2 state in 206 Pb 4. Conclusions

Introduction

Introduction

ΔρC [fm-3] Measured charge density difference between the isotones 206 Pb and 205 Tl r [fm] Solid Line: Adjusted mean field calculation assuming a difference in occupation probabilities of 0. 7 in the 3 s shell and 0. 3 in the 2 d shell

Formalism Single-particle Schrodinger Eq. Experimentally, one measures density:

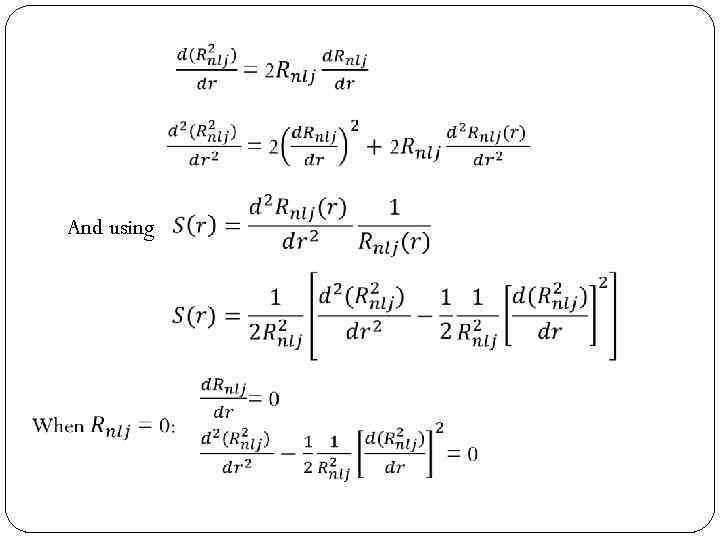And using

Using the relation:

Examples of application of method for 3 s 1/2: We get constant potential: Harmonic Oscillator: We get expected potential:

For commonly used potential, Woods-Saxon potential: Coulomb potential for equivalent uniform charge distribution: Spin-orbit potential: c ~ 0. 2

Determining point proton distribution from charge distribution Experimentally

Define Fourier transform of density: We get the point proton density:

Rearrangement effect : The charge distribution of 205 Tl is scaled so that the charge rms radius of the scaled density is equal to that of the 81 core protons in 206 Pb.

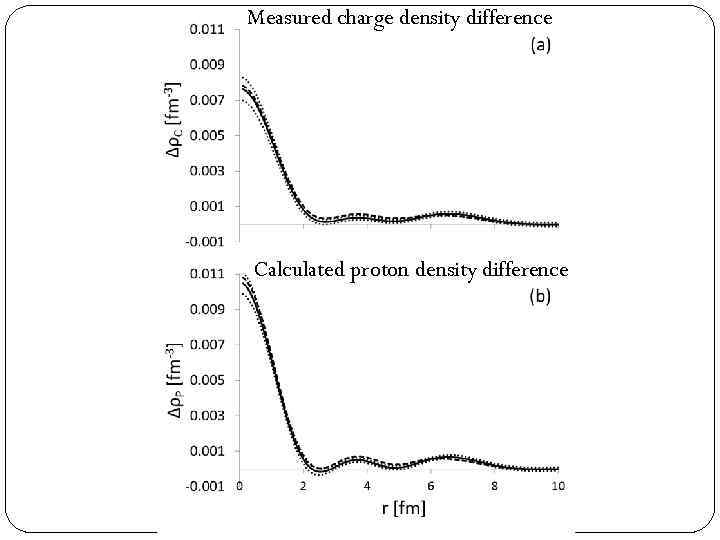Measured charge density difference Calculated proton density difference

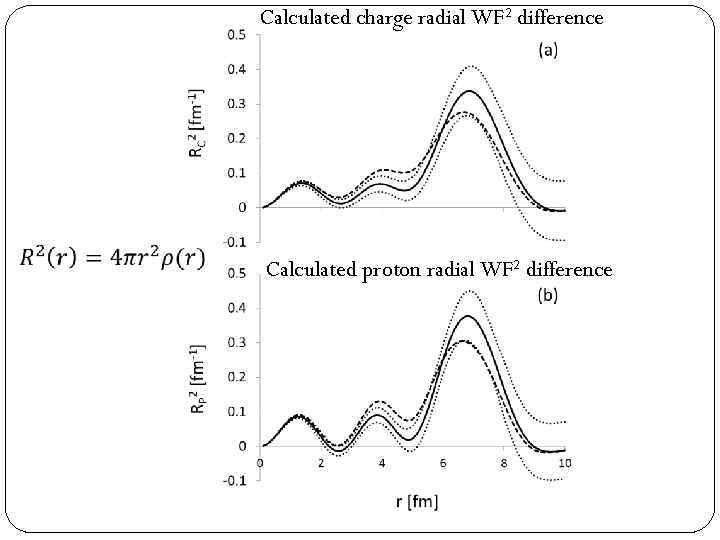Calculated charge radial WF 2 difference Calculated proton radial WF 2 difference

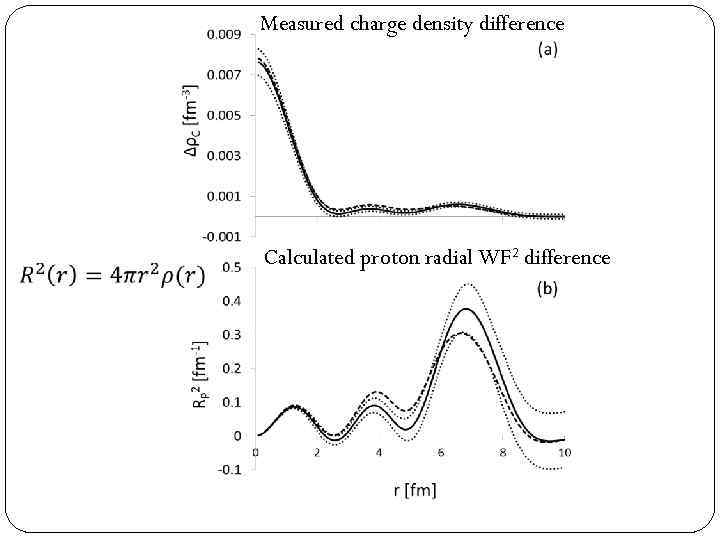Measured charge density difference Calculated proton radial WF 2 difference

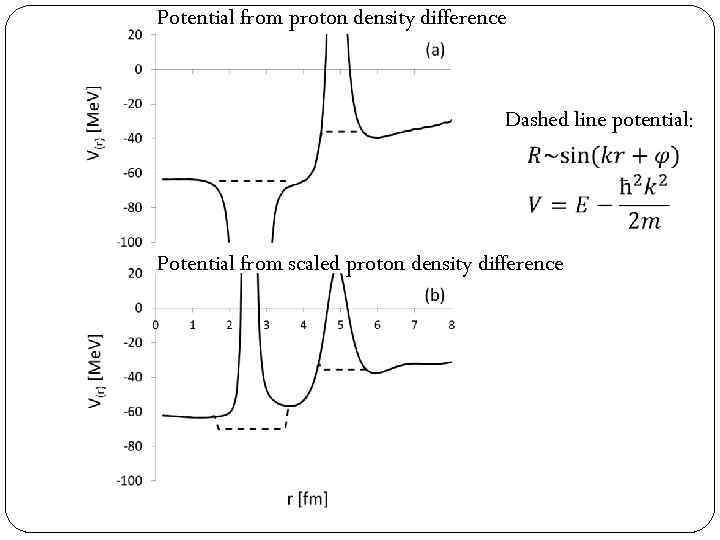Potential from proton density difference Dashed line potential: Potential from scaled proton density difference

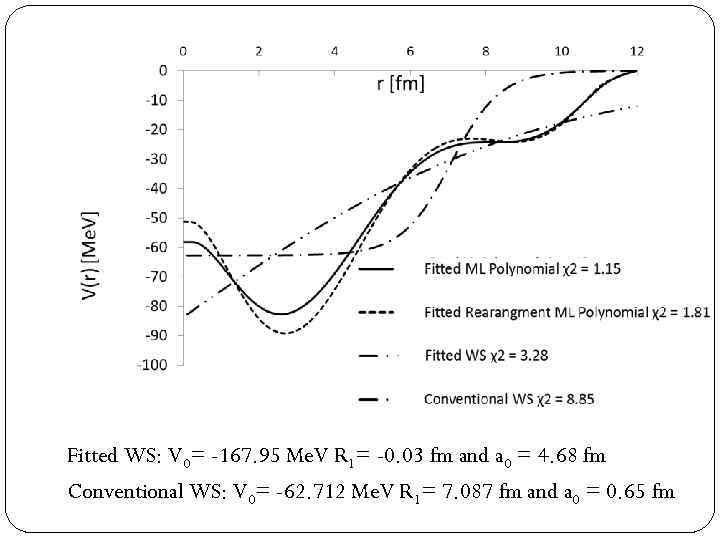Fitted WS: V 0= -167. 95 Me. V R 1= -0. 03 fm and a 0 = 4. 68 fm Conventional WS: V 0= -62. 712 Me. V R 1= 7. 087 fm and a 0 = 0. 65 fm

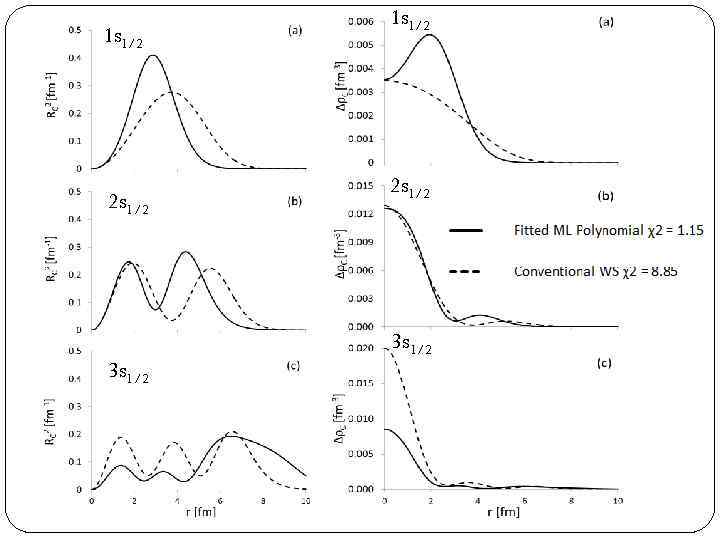1 s 1/2 2 s 1/2 3 s 1/2

Conclusions We have developed a new method of determining the single particle potential directly from the density distributions The potential derived from the density distributions of 3 s 1/2 state in 206 Pb shows large uncertainties around the nodes as the experimental error is larger than the value of the density We carried out a least-squares fit of a potential that is fit to the density data which is a much better fit than the conventional Woods-Saxon potential especially near r = 0 fm Clearly more accurate data is needed to better determine the potential and answer the question how well can the data be reproduced by a calculated 3 s 1/2 wave function

Acknowledgements TAMU and Cyclotron Institute DOE support

Backup Slides