A Non-Probabilistic Generalization of the Agreement Theorem

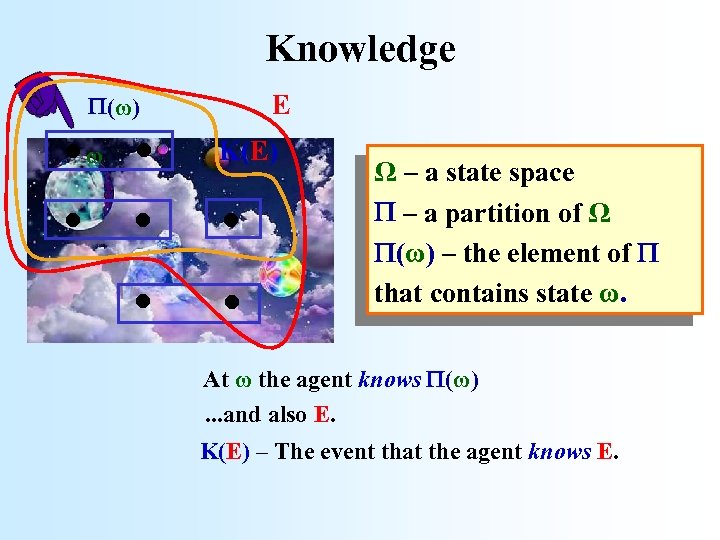
Knowledge . . . . (ω) ω E K(E) Ω – a state space – a partition of Ω (ω) – the element of that contains state ω. At ω the agent knows (ω). . . and also E. K(E) – The event that the agent knows E.

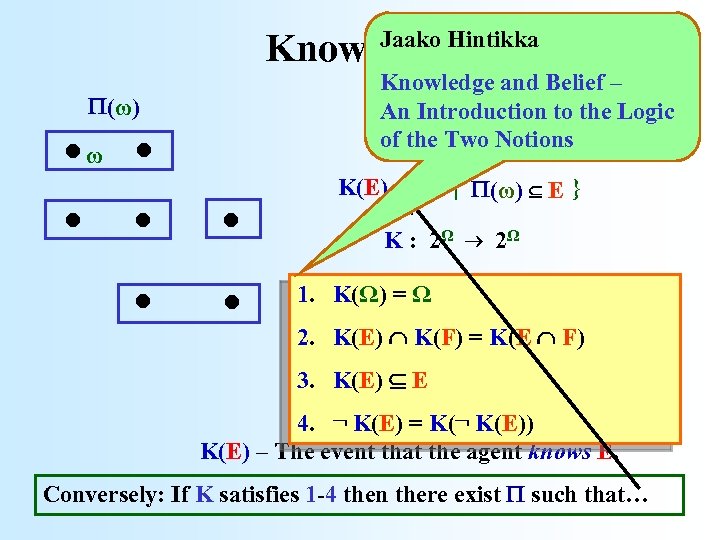
Jaako Hintikka Knowledge . . . . (ω) ω Knowledge and Belief – An Introduction to the Logic of the Two Notions K(E) = {ω | (ω) E } K : 2Ω 2Ω 1. K(Ω) = Ω 2. K(E) K(F) = K(E F) 3. K(E) E 4. ¬ K(E) = K(¬ K(E)) K(E) – The event that the agent knows E. Conversely: If K satisfies 1 -4 then there exist such that…

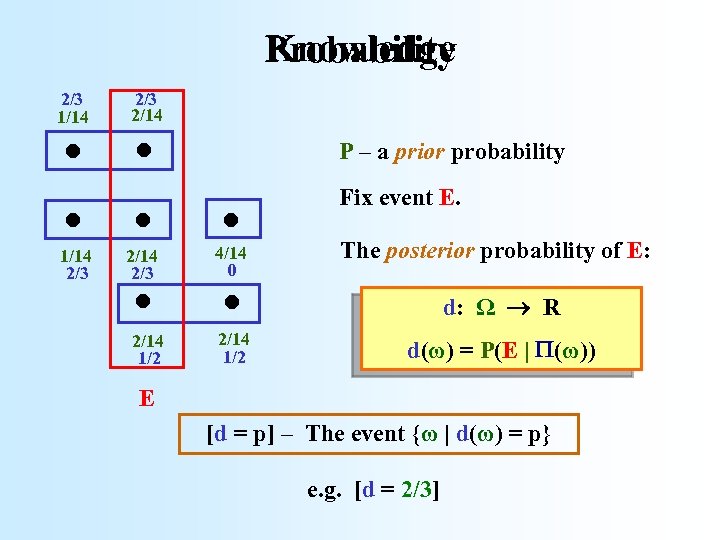
Knowledge Probability . . . . 2/3 1/14 2/3 2/14 1/2 4/14 0 2/14 1/2 P – a prior probability Fix event E. The posterior probability of E: d: Ω R d(ω) = P(E | (ω)) E [d = p] – The event {ω | d(ω) = p} e. g. [d = 2/3]

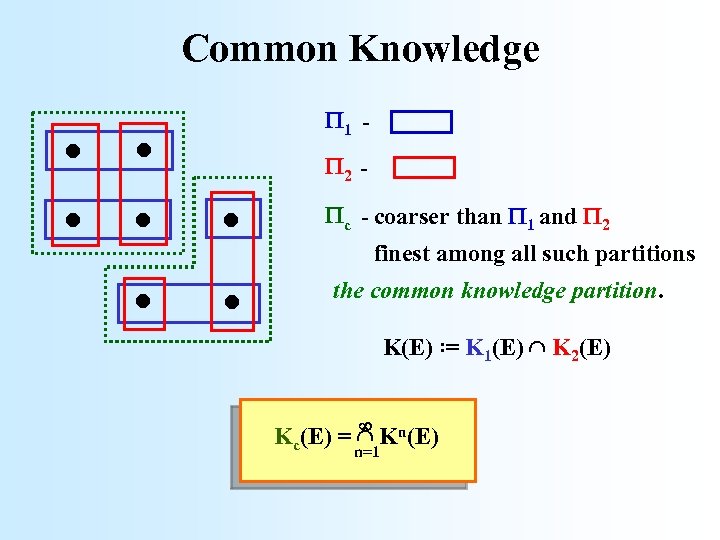
Common Knowledge . . . . 1 2 c - coarser than 1 and 2 finest among all such partitions the common knowledge partition. K(E) : = K 1(E) K 2(E) Kc(E) = Kn(E) n=1

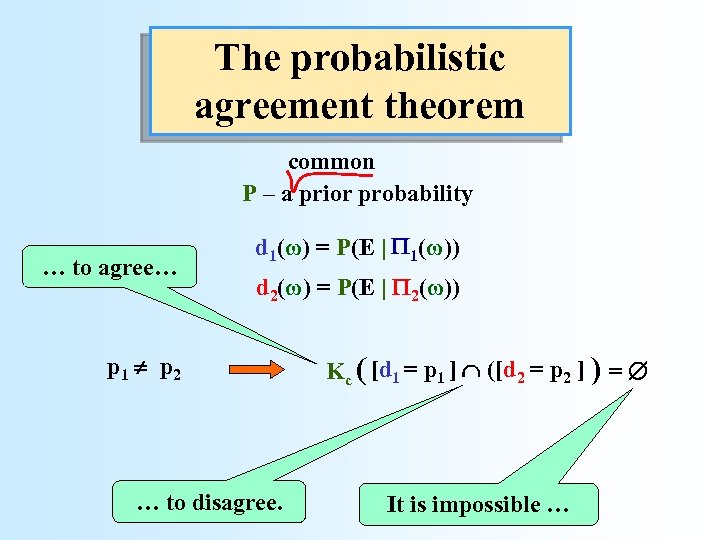
The probabilistic agreement theorem common P – a prior probability … to agree… d 1(ω) = P(E | 1(ω)) d 2(ω) = P(E | 2(ω)) p 1 p 2 … to disagree. Kc ( [d 1 = p 1 ] ([d 2 = p 2 ] ) = It is impossible …

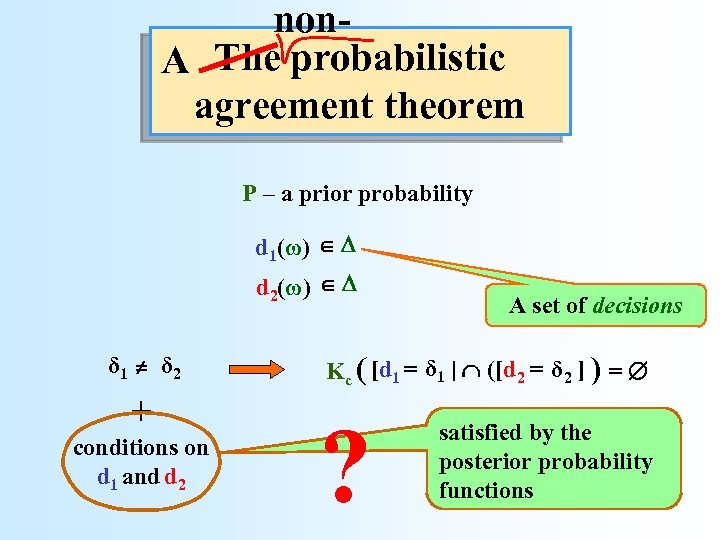
non. A The probabilistic agreement theorem P – a prior probability d 1(ω) = P(E | 1(ω)) d 2(ω) = P(E | 2(ω)) δ δ p 1 p 2 + conditions on d 1 and d 2 A set of decisions δ δ Kc ( [d 1 = p 1 ] ([d 2 = p 2 ] ) = ? satisfied by the posterior probability functions

Virtual decision functions D : 2Ω A decision function di : Ω is derived from the virtual decision function D if di (ω) = D( i (ω)) Agents are like minded if all individual decision functions Interpretation: D(E) is the are derived from the same virtual decision function. decision made if E were the information given Cave, J. (1983), Learning to agree, Economics Letters, 12. to the agent. Bacharach, M. (1985), Some extensions of a claim of Aumann in an axiomatic model of knowledge, J. Econom. Theory, 37(1).

The Sure Thing Principle (STP) A businessman contemplates buying a certain piece of property. He considers the outcome of the next presidential election relevant. So, to clarify the matter to himself, he asks whether he would buy if he knew that The sure-thing principle going appropriately be accepted would. the Democratic candidate werecannot to win, and decides that heas postulate in the sense that P 1 he would buy if he knew that Similarly, he considers whether is, because it would introduce new the undefined technical terms referring to knowledge and that he would. Republican candidate were going to win, and again finds possibility Seeingthat would render it in either event, he decides that stillshould buy, that he would buy mathematically useless without he more postulates governing these terms. It will be preferable to regard even though he does not know which event obtains, or will obtain, as we would the principle as is all too seldom thatsuggests certain arrived at on ordinarily say. It a loose one that a decision can be formal postulate well articulated except the basis of this principle, butwith P 1. possibly of for the assumption of simple ordering, I know of no other extralogical principle governing decisions that finds such ready acceptance. Savage, L. J. (1954), The foundations of statistics.

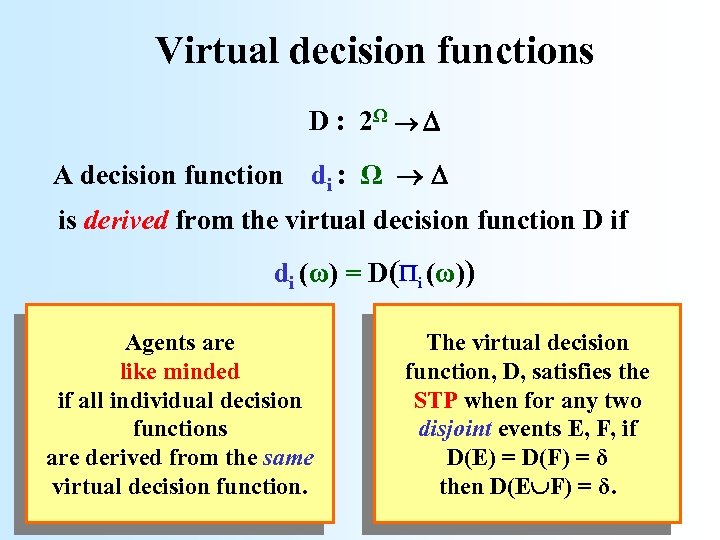
Virtual decision functions D : 2Ω A decision function di : Ω is derived from the virtual decision function D if di (ω) = D( i (ω)) Agents are like minded if all individual decision functions are derived from the same virtual decision function. The virtual decision function, D, satisfies the STP when for any two disjoint events E, F, if D(E) = D(F) = δ then D(E F) = δ.

An agreement theorem If the agents are § like minded with virtual decision function D, and § D satisfies STP, then it is impossible to agree to disagree. That is, if the decisions of the agents are common knowledge then they coincide.

A detective story A murder has been committed. To increase the chances of conviction, the chief of police puts two detectives on the case, with strict instructions to work independently, to exchange no information. The two, Alice and Bob, went to the same police school; so given the same clues, they would reach the same conclusions. But as they will work independently, they will, presumably; not get the same clues. At the end of thirty days, each is to decide whom to arrest (possibly nobody). Like mindedness

A detective story On the night before thirtieth day, they happen to meet … and get to talking about the case. True to their instructions, they exchange no substantive information, no clues; but … feel that there is no harm in telling each other whom they plan to arrest. Thus, … it is common knowledge between them whom each will arrest. Conclusion: They arrest the same people; and this, in spite of knowing nothing about each other's clues. Curtain

A detective story Aumann, (1988) (1999) Notes on interactive epistemology, IJGT. unpublished.

Is the STP captured? How do virtual decision functions fit in a Is the agent more knowledgeable in ω than in ω’ ? partitional knowledge setup? Syntactically, they involve knowledge that cannot be expressed in terms of actual knowledge Ki. Semantically, at a given state ω the agent’s knowledge is given by i(ω) and not by any other event. (Moses & Nachum (1990)) Ki p ¬ Ki p . . ω’ ω i(ω) i(ω’) A remedy ¬ Ki p Ki ¬ Ki p

Comparison of knowledge i knows at ω … more than … i knows at ω’. The event that i is more knowledgeable than j: . ω [i j] : = (¬ Kj(E) Ki(E)) E intra personal interstate inter state intra personal . ω’ interstate i knows at ω … more than . … j knows at ω. ω ω ¬ Kj(E) Ki(E) for each E.

Interpersonal Sure Thing Principle (ISTP) The decision functions (d 1, …, dn) satisfy the ISTP if for each i and j: Kj( [i j] ) [di = δ] ) [dj = δ] [i = j] : = [i j] [j i] If the decision functions satisfy ISTP, then the agents are like minded: For each i and j, [i = j] [di = di]

Expandability The decision functions (d 1, …, dn) on the model (Ω, K 1 , … , Kn ) are ISTP-expandable if for each expansion (Ω, K 1 , … , Kn+1 ) there exists a decision dn+1 for agent n+1 such that (d 1, …, dn+1) satisfy the ISTP. An agent is epistemic dummy, if it is common knowledge that each other agent is more knowledgeable. Where n+1 is epistemic dummy Officer E. P. Dummy

A non-probabilistic generalization of the agreement theorem If the decision functions (d 1, …, dn) on the model (Ω, K 1 , … , Kn ) are ISTP-expandable then the agents cannot agree to disagree.

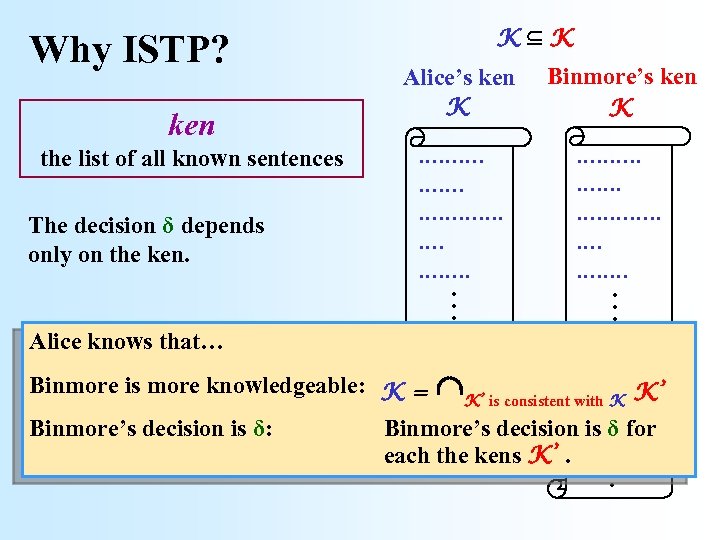
the list of all known sentences The decision δ depends only on the ken. Alice knows that… Binmore’s ken K . . . . . ken Alice’s ken K . . . Why ISTP? K K . . . …. . Binmore is more knowledgeable: K = K’ is consistent with K K’ … Binmore’s decision is δ: Binmore’s decision. . is δ for each the kens K’.