A Nitzan Tel Aviv University SELECTED TOPICS IN

A. Nitzan, Tel Aviv University SELECTED TOPICS IN CHEMICAL DYNAMICS IN CONDENSED SYSTEMS Boulder, Aug 2007 Lecture 1

Introduction

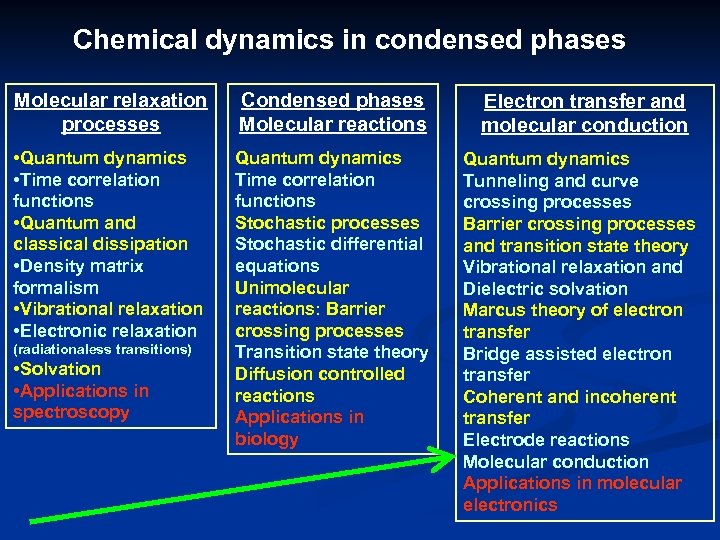Chemical dynamics in condensed phases Molecular relaxation processes Condensed phases Molecular reactions Electron transfer and molecular conduction • Quantum dynamics • Time correlation functions • Quantum and classical dissipation • Density matrix formalism • Vibrational relaxation • Electronic relaxation Quantum dynamics Time correlation functions Stochastic processes Stochastic differential equations Unimolecular reactions: Barrier crossing processes Transition state theory Diffusion controlled reactions Applications in biology Quantum dynamics Tunneling and curve crossing processes Barrier crossing processes and transition state theory Vibrational relaxation and Dielectric solvation Marcus theory of electron transfer Bridge assisted electron transfer Coherent and incoherent transfer Electrode reactions Molecular conduction Applications in molecular electronics (radiationaless transitions) • Solvation • Applications in spectroscopy

electron transport in molecular systems Reviews: Annu. Rev. Phys. Chem. 52, 681– 750 (2001) Science, 300, 1384 -1389 (2003); MRS Bulletin, 29, 391 -395 (2004); Bulletin of the Israel Chemical Society, Issue 14, p. 3 (2003) (Hebrew) J. Phys. : Condens. Matter 19, 103201 (2007) Thanks I. Benjamin, D. Beratan, A. Burin, G. Cuniberty, B. Davis, S. Datta, D. Evans, B. Feinberg, M. Galperin, A. Ghosh, H. Grabert, P. Hänggi, G. Ingold, M. Jouravlev, J. Jortner, S. Kohler, R. Kosloff, A. Landau, L. Kronik, J. Lehmann, M. Majda, A. Mosyak, V. Mujica, R. Naaman, F. v Oppen, U. Peskin, M. Ratner, D. Segal, T. Seideman, S. Skourtis, H. Tal-Ezer, A. Troisi, S. Tornow

Molecular conduction

Molecular Rectifiers Arieh Aviram and Mark A. Ratner IBM Thomas J. Watson Research Center, Yorktown Heights, New York 10598, USA Department of Chemistry, New York University, New York 10003, USA Received 10 June 1974 Abstract The construction of a very simple electronic device, a rectifier, based on the use of a single organic molecule is discussed. The molecular rectifier consists of a donor pi system and an acceptor pi system, separated by a sigmabonded (methylene) tunnelling bridge. The response of such a molecule to an applied field is calculated, and rectifier properties indeed appear.

Xe on Ni(110)

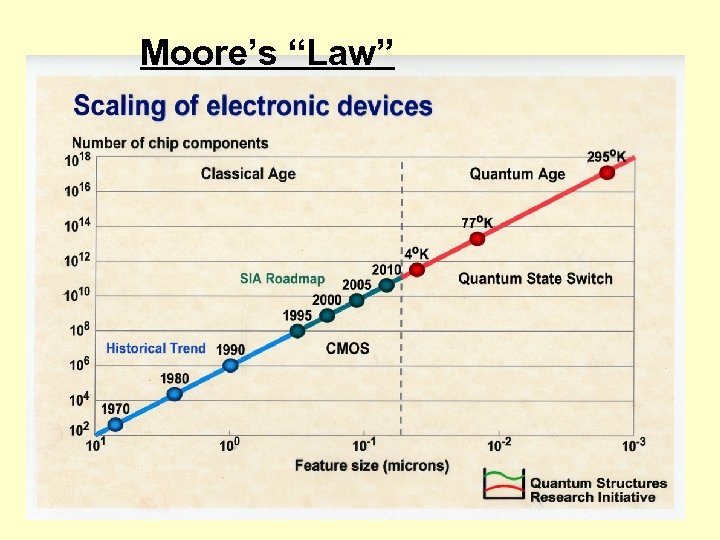Moore’s “Law”

IEEE TRANSACTIONS ON ELECTRON DEVICES VOL. 43 OCTOBER 1996 1637 Need for Critical Assessment Rolf Landauer, Life Fellow, IEEE Abstract Adventurous technological proposals are subject to inadequate critical assessment. It is the proponents who organize meetings and special issues. Optical logic, mesoscopic switching devices and quantum parallelism are used to illustrate this problem. Feynman: For a successful Technology, reality must take precedence over public relations, for nature cannot be fooled

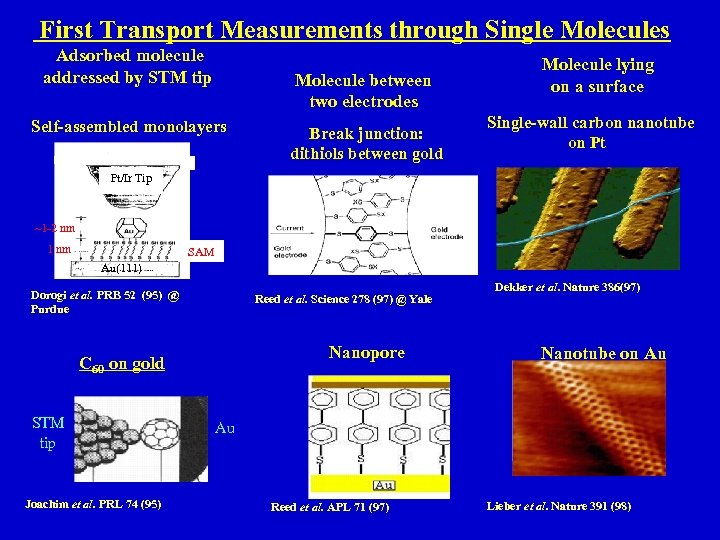First Transport Measurements through Single Molecules Adsorbed molecule addressed by STM tip Molecule between two electrodes Self-assembled monolayers Break junction: dithiols between gold Molecule lying on a surface Single-wall carbon nanotube on Pt Pt/Ir Tip ~1 -2 nm 1 nm SAM Au(111) Dorogi et al. PRB 52 (95) @ Purdue Reed et al. Science 278 (97) @ Yale Nanopore C 60 on gold STM tip Joachim et al. PRL 74 (95) Dekker et al. Nature 386(97) Nanotube on Au Au Reed et al. APL 71 (97) Lieber et al. Nature 391 (98)

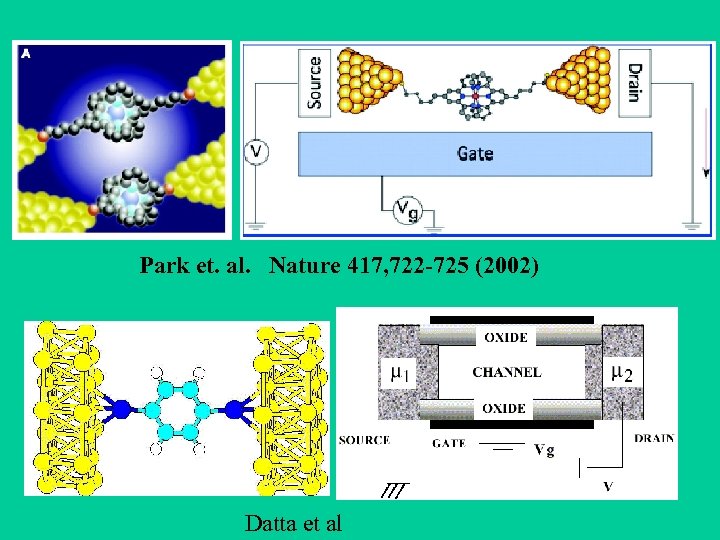Park et. al. Nature 417, 722 -725 (2002) Datta et al

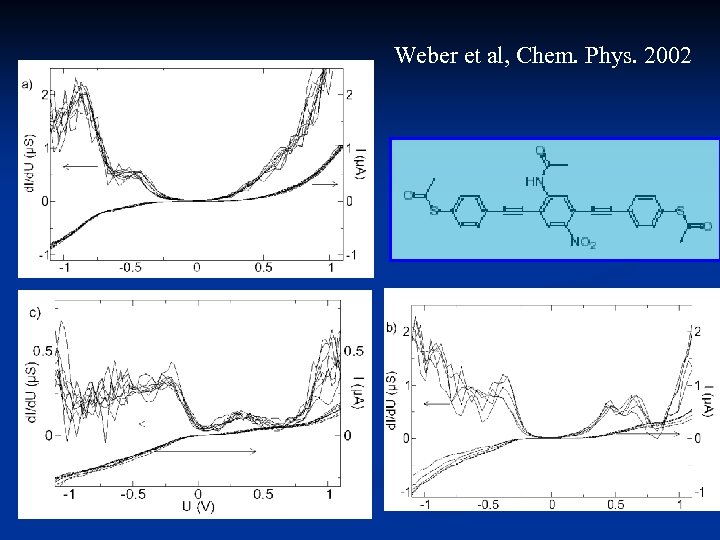Weber et al, Chem. Phys. 2002

b=0. 43Å-1 Xu et al (Tao), Nano. Let (2004) loge of GCGC(AT)m. GCGC conductance vs length (total number of base pairs). The solid line is a linear fit that reflects the exponential dependence of the conductance on length. The decay constant, b , is determined from the slope of the linear fit. (b) Conductance of (GC)n vs 1/length (in total base pairs).

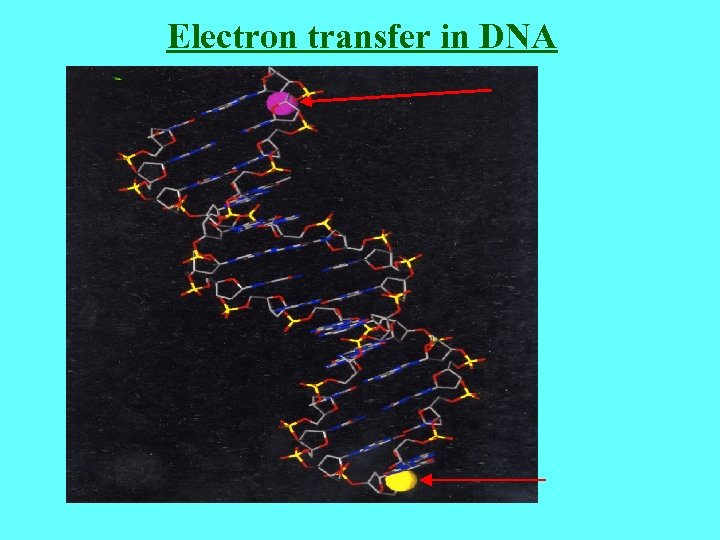Electron transfer in DNA

Electron transmission processes in molecular systems Electron transfer n Electron transmission n Conduction n Parameters that affect molecular conduction n Eleastic and inelastic transmission n Coherent and incoherent conduction n Heating and heat conduction n Possible interaction with light n

Chemical processes Gas phase reactions n n n Follow individual collisions States: Initial Final Energy flow between degrees of freedom Mode selectivity Yields of different channels Reactions in solution n Effect of solvent on mechanism Effect of solvent on rates Dependence on solvation, relaxation, diffusion and heat transport.

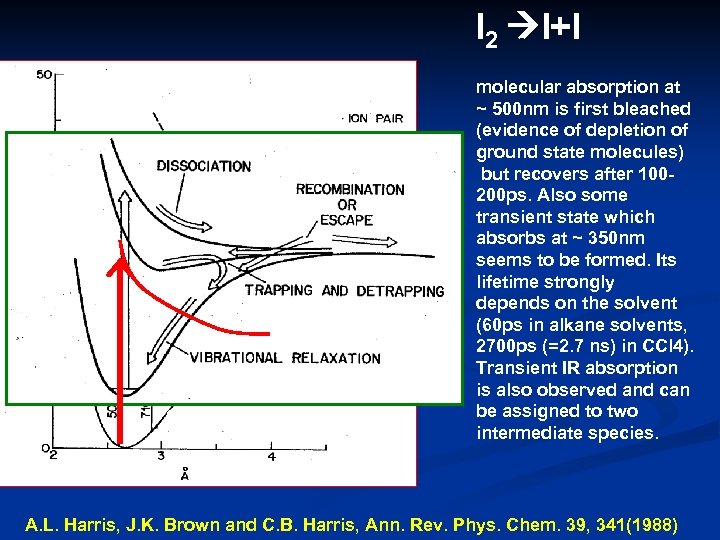I 2 I+I molecular absorption at ~ 500 nm is first bleached (evidence of depletion of ground state molecules) but recovers after 100200 ps. Also some transient state which absorbs at ~ 350 nm seems to be formed. Its lifetime strongly depends on the solvent (60 ps in alkane solvents, 2700 ps (=2. 7 ns) in CCl 4). Transient IR absorption is also observed and can be assigned to two intermediate species. A. L. Harris, J. K. Brown and C. B. Harris, Ann. Rev. Phys. Chem. 39, 341(1988)

The hamburger-dog dilemma as a lesson in the importance of timescales

TIMESCALES Typical molecular timescales in chemistry and biology (adapted from G. R. Fleming and P. G. Wolynes, Physics today, May 1990, p. 36).

Boulder August 2007 (3) Molecular conduction (2) Electron transfer Chapter 13 -15 Chapter 16 Chapter 17 (1) Relaxation and conductions • Simple models for molecularreactions in (4) Recent research transfer at processes • Factors affecting electron condensed molecular systems (a) Inelastic issues in molecular • Simple interfaces models • Kinetic models conduction • The Landauer formula • Marcus theory • Transition state redox • Molecular conduction by the Landauer (b) Tunneling troughtheory • The reorganization energy • Kramers theory and its extensions formula molecular species • Adiabatic and non-adiabatic • Low, high and intermediate • Relationship to electron-transfer rates. (c) Molecular heating and limits • Structure-function effects in molecular friction regimes molecular heatreactions • Solvent conduction controlled conduction • Diffusion be done with controlled reactions (d) What assisted electronon a • Bridge can • How does the potential drop transfer photons? molecule and this is important • Coherent why incoherent • Probing molecules in STM junctions transfer • Electron transfer by hopping • Electrode processes

PART A Relaxation and reactions in molecular systems

Molecular processes in condensed phases and interfaces • Diffusion Molecular timescales • Relaxation Diffusion D~10 -5 cm 2/s • Solvation • Nuclear rerrangement • Charge transfer (electron and xxxxxxxxproton) • Solvent: an active spectator – energy, friction, solvation Electronic 10 -16 -10 -15 s Vibraional 10 -14 s Vibrational xxxxrelaxation 1 -10 -12 s Chemical reactions xxxxx 1012 -10 -12 s Rotational 10 -12 s Collision times 10 -12 s

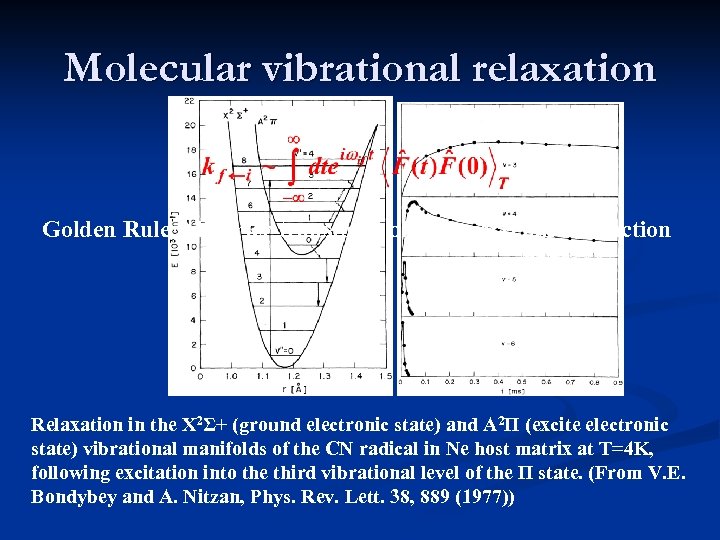Molecular vibrational relaxation Golden Rule Fourier transform of bath correlation function Relaxation in the X 2Σ+ (ground electronic state) and A 2Π (excite electronic state) vibrational manifolds of the CN radical in Ne host matrix at T=4 K, following excitation into the third vibrational level of the Π state. (From V. E. Bondybey and A. Nitzan, Phys. Rev. Lett. 38, 889 (1977))

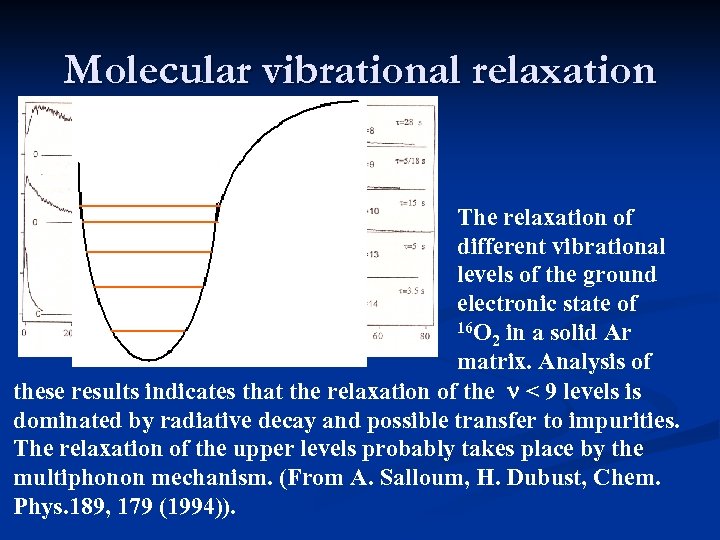Molecular vibrational relaxation The relaxation of different vibrational levels of the ground electronic state of 16 O in a solid Ar 2 matrix. Analysis of these results indicates that the relaxation of the n < 9 levels is dominated by radiative decay and possible transfer to impurities. The relaxation of the upper levels probably takes place by the multiphonon mechanism. (From A. Salloum, H. Dubust, Chem. Phys. 189, 179 (1994)).

Frequency dependent friction MARKOVIAN LIMIT WIDE BAND APPROXIMATION

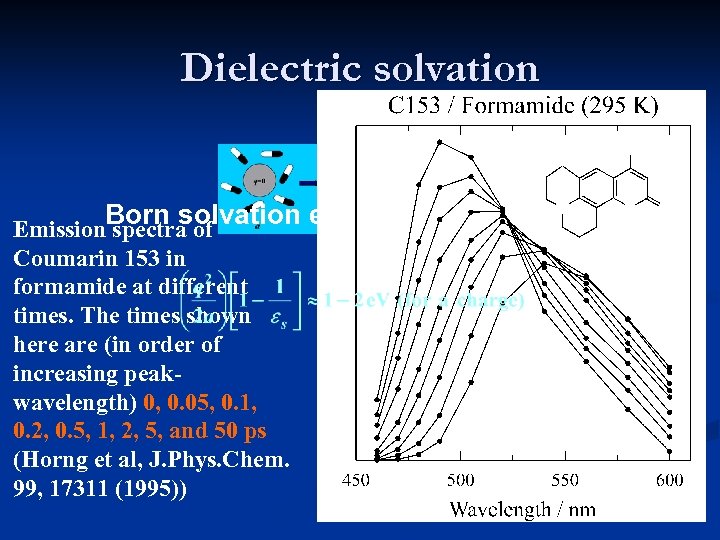Dielectric solvation Born solvation energy Emission spectra of Coumarin 153 in formamide at different times. The times shown here are (in order of increasing peakwavelength) 0, 0. 05, 0. 1, 0. 2, 0. 5, 1, 2, 5, and 50 ps (Horng et al, J. Phys. Chem. 99, 17311 (1995))

Continuum dielectric theory of solvation How does solvent respond to a sudden change in the molecular charge distribution? (Poisson equation) Dielectric Electric Debye dielectric relaxation model displacement function field Electronic response polarization Dielectric susceptibility Total (static) response Debye relaxation time

Continuum dielectric theory of solvation WATER: t. D=10 ps t. L=125 fs

“real” solvation “Newton” dielectric The experimental solvation function for water using sodium salt of coumarin-343 as a probe. The line marked ‘expt’ is the experimental solvation function S(t) obtained from the shift in the fluorescence spectrum. The other lines are obtained from simulations [the line marked ‘Δq’ –simulation in water. The line marked S 0 –in a neutral atomic solute with Lennard Jones parameters of the oxygen atom]. (From R. Jimenez et al, Nature 369, 471 (1994)).

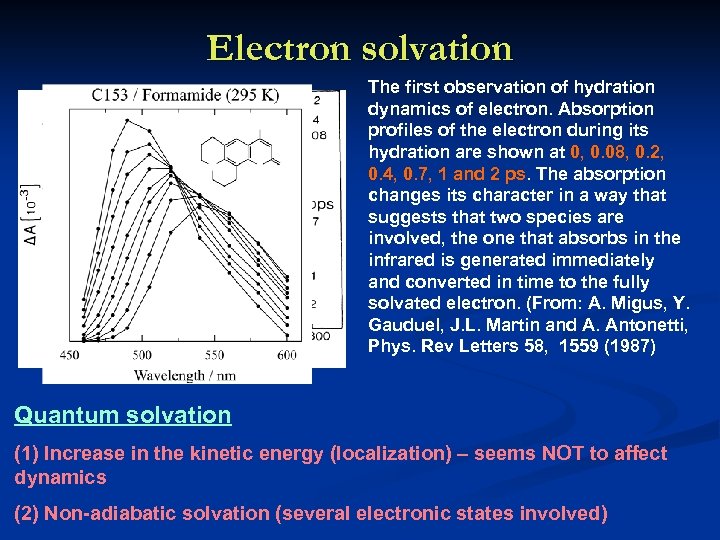Electron solvation The first observation of hydration dynamics of electron. Absorption profiles of the electron during its hydration are shown at 0, 0. 08, 0. 2, 0. 4, 0. 7, 1 and 2 ps. The absorption changes its character in a way that suggests that two species are involved, the one that absorbs in the infrared is generated immediately and converted in time to the fully solvated electron. (From: A. Migus, Y. Gauduel, J. L. Martin and A. Antonetti, Phys. Rev Letters 58, 1559 (1987) Quantum solvation (1) Increase in the kinetic energy (localization) – seems NOT to affect dynamics (2) Non-adiabatic solvation (several electronic states involved)

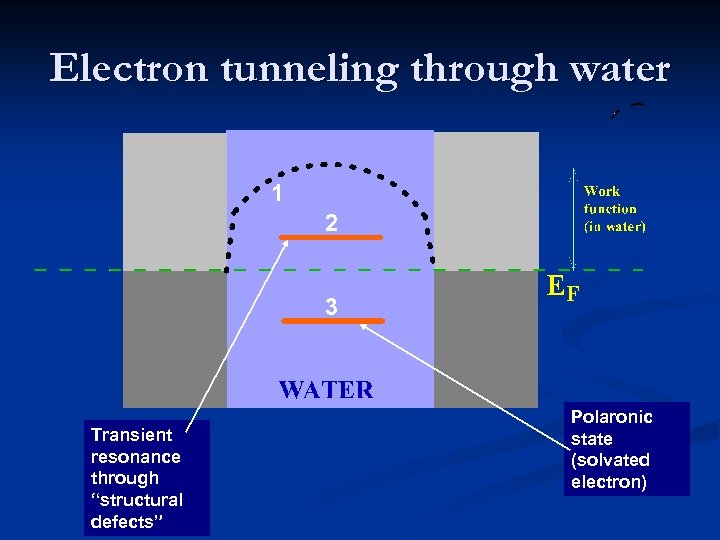Electron tunneling through water 1 2 3 Transient resonance through “structural defects” Polaronic state (solvated electron)

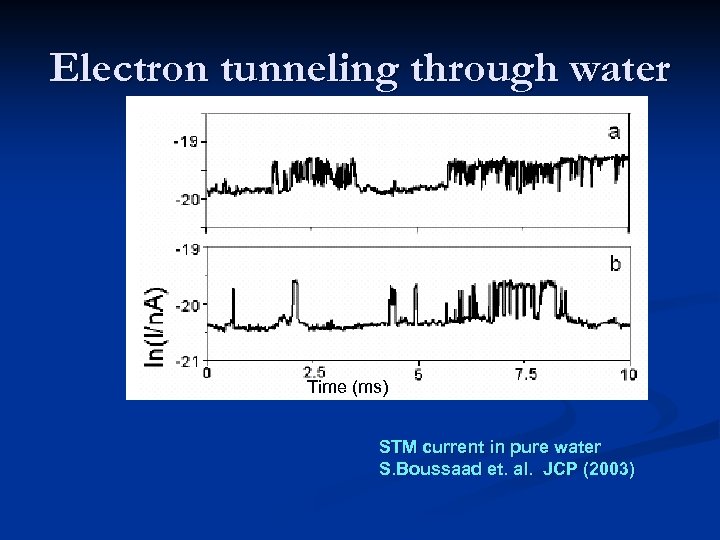Electron tunneling through water Time (ms) STM current in pure water S. Boussaad et. al. JCP (2003)

Chemical reactions in condensed phases ØBimolecular ØUnimolecular Diffusion controlled rates diffusion R

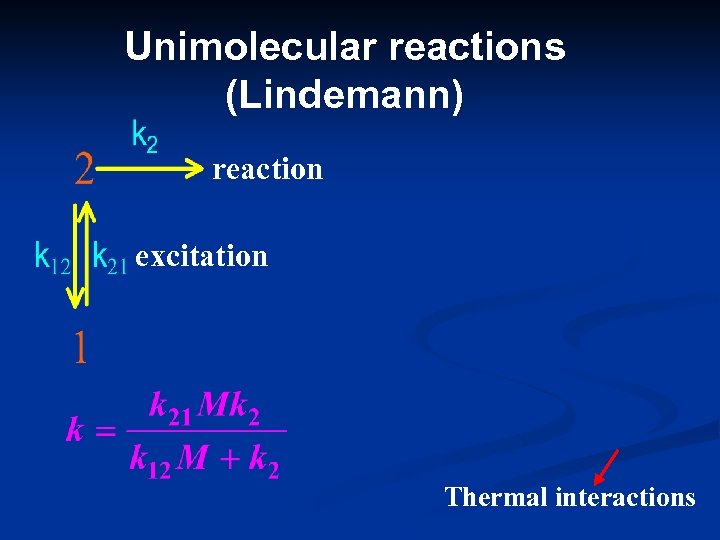Unimolecular reactions (Lindemann) reaction excitation Thermal interactions

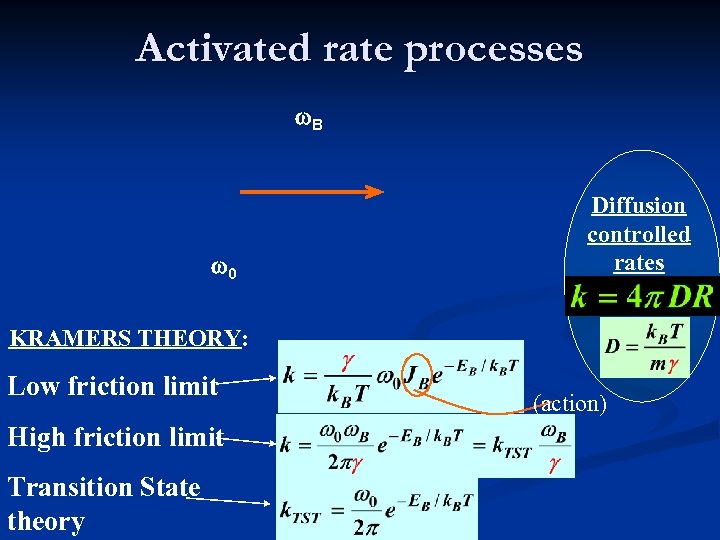Activated rate processes w. B w 0 Diffusion controlled rates KRAMERS THEORY: Low friction limit High friction limit Transition State theory (action)

Effect of solvent friction TST A compilation of gas and liquid phase data showing the turnover of the photoisomerization rate of trans stilbene as a function of the “friction” expressed as the inverse self diffusion coefficient of the solvent (From G. R. Fleming and P. G. Wolynes, Physics Today, 1990). The solid line is a theoretical fit based on J. Schroeder and J. Troe, Ann. Rev. Phys. Chem. 38, 163 (1987)).

The physics of transition state rates Assume: (1) Equilibrium in the well (2) Every trajectory on the barrier that goes out makes it

The (classical) transition state rate is an upper bound • Assumed equilibrium in the well – in reality population will be depleted near the barrier • Assumed transmission coefficient unity above barrier top – in reality it may be less

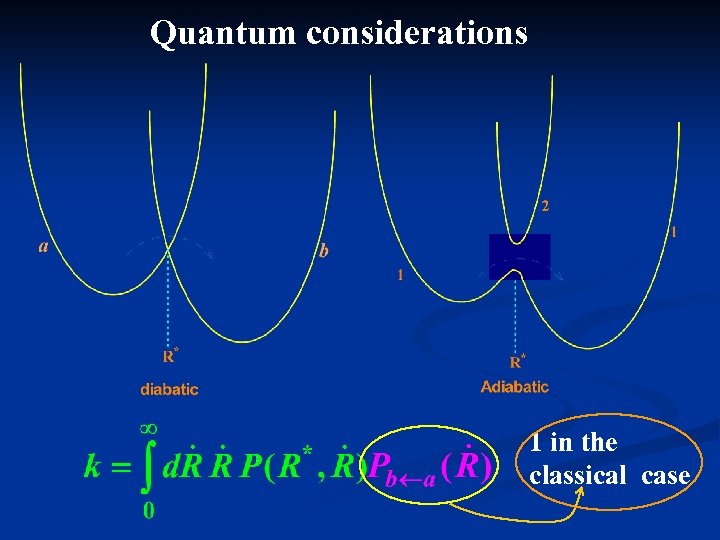Quantum considerations 1 in the classical case