A Method for Determining Turbine Airfoil Geometry Parameters

A Method for Determining Turbine Airfoil Geometry Parameters from a Set of Coordinates ME 597 Project I – Spring 2006 Purdue School of Engineering and Technology, IUPUI Andrew White, BPMME Project Advisors: Dr. Hasan Akay, IUPUI Ed Turner, Rolls-Royce Corporation Presented on April 27, 2006

Outline • • • Project Terminology Problem Description Project Objective Overview of Solution – Two Approaches Previous Work Optimization Challenges Project Optimization Process Objective Function Description Quasi-Newton Optimization Methods – DFP – NLPQL • Results: – Objective Function Mapping – 1 Parameter Optimization – 3 Parameter Optimization • Conclusions • Future Study

This project focuses on the cross-sectional shapes of Turbine Airfoils of a Rolls-Royce Trent 1000 gas turbine engine

Project Terminology • Airfoil – Leading/trailing edge – Pressure/Suction surface • Parameters – BETA 1 – β 1 – DELTABETA 1 – Δβ 1 – LE (a/b) Suction Surface • Objective function – Baseline vs. New • Target vs. Starting airfoil • Commercial vs. In-house code • Mapping vs. Optimizing (Objective function) Leading Edge Pressure Surface Trailing Edge

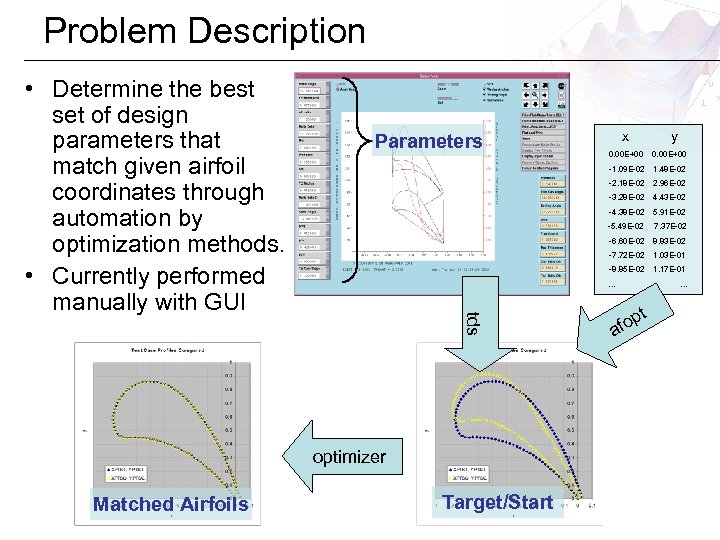
Problem Description Parameters y 0. 00 E+00 1. 48 E-02 -2. 18 E-02 2. 96 E-02 -3. 28 E-02 4. 43 E-02 -4. 38 E-02 5. 91 E-02 -5. 49 E-02 7. 37 E-02 -6. 60 E-02 8. 83 E-02 -7. 72 E-02 1. 03 E-01 -8. 85 E-02 1. 17 E-01 … optimizer Matched Airfoils x -1. 09 E-02 tds • Determine the best set of design parameters that match given airfoil coordinates through automation by optimization methods. • Currently performed manually with GUI Target/Start … t p afo

Project Objectives • 3 main objectives for the problem: – Develop an optimizable objective function – Use a commercial optimization/design code to test objective function behavior – Understand theory/programming of an in-house numerical optimization code and set it up for future optimization of the present problem in place of the commercial code

Overview of Solution – Two Approaches Solve shape matching through optimization by… Commercial Code • Optimization: NLPQL (Non-Linear Programming by Quadratic approximation of the Lagrangian) • GUI • Relatively “easy” • Less control, must understand available methods • Single user per $xx, 000 license In-house code • Optimization: DFP (Davidon-Fletcher-Powell) • FORTRAN • Must understand code • More control over code, uses trusted optimization method • Many users • This project used the commercial code to develop an objective function while preparing the in-house code for future work

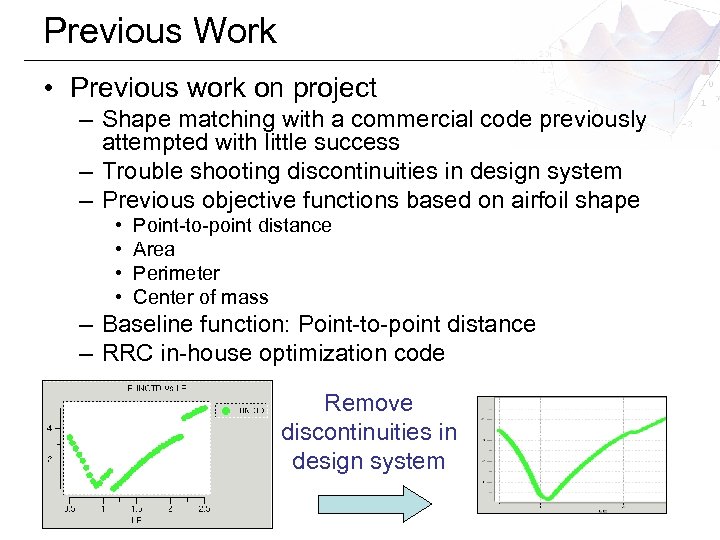
Previous Work • Previous work on project – Shape matching with a commercial code previously attempted with little success – Trouble shooting discontinuities in design system – Previous objective functions based on airfoil shape • • Point-to-point distance Area Perimeter Center of mass – Baseline function: Point-to-point distance – RRC in-house optimization code Remove discontinuities in design system

Optimization Challenges • Errors in mathematical formulation of models which no mere parameter adjustments can hope to compensate for* • Objective function sensitivity/behavior can be difficult to predict in entire design space • Can be difficult to tell if problems are due to objective function or mathematical model • Optimizer algorithms generally perform more and more poorly the larger the number of varying parameters* • Choosing the “right” optimization routine “The best optimization routine is the one you know best. ” --Papalambros and Wilde, Principles of Optimal Design *Source: http: //nsr. bioeng. washington. edu/PLN/Members/butterw/JSIMDOC 1. 6/Contents. stx/User_Intro. stx

Project Optimization Process Starting Design Parameters Airfoil Design System (generates airfoil geometry coordinates from 15 input design parameters) Airfoil coordinates from parameters Target airfoil coordinates Objective Function (Airfoil comparator function) Objective function value, F NLPQL/DFP optimizer (changes parameters to minimize F) Modified design parameters

Optimization Overview • Optimization requires: – Objective function: what to optimize – Optimization routine: how to let a computer make the objective function as small as possible • Next: – Objective function description – Basics of quasi-Newton optimization methods – Two quasi-Newton methods used in this project: • DFP – Davidon-Fletcher-Powell • NLPQL – Non-Linear Programming by Quadratic approximation of the Lagrangian

Objective Function Description • Scalar expression that should approach zero when the two airfoils match • Objective functions: – Baseline: Point-to-point distance – Energy Measure – New Energy Measure Parameterized Airfoil Target Parameterized Difference Measure

Objective Function Description (cont’d) • Energy Measure objective function from computer vision shape recognition application (Cohen et al) where, KQ(s') s' Q Q(s') – P(s) P s=0 KP(s) s=1 s Discretization for computer code by trapezoidal quadrature formula…

Objective Function Description (cont’d) • Modified Energy Measure objective function: – Removed radius of curvature coefficient – Integrated curvature on pressure and suction surfaces only Energy Measure New Energy Measure Removed curvature from integral on leading edge

Quasi-Newton Optimization Methods • What are Quasi-Newton methods? † – Quasi-Newton methods build up curvature information (i. e. 2 nd derivative) at each iteration to formulate a quadratic model problem of the form: H = Hessian matrix c = gradient vector b = constant scalar – The optimal solution for this problem occurs when the partial derivatives of x go to zero, i. e. , – The optimal solution point, x*, can be written as – Quasi-Newton methods approximate H-1 using f(x) and grad f(x) to build up curvature information with an iterative updating technique. Quadratic Model approximation of “Design surface” †Source: http: //www. mathworks. com/access/helpdesk/help/toolbox/optim/ug/f 137. html x

Optimization Method I – DFP • DFP algorithm* – Davidon-Fletcher-Powell *Source: References [1] through [4]

Optimization Method II – NLPQL • NLPQL algorithm* (Nonlinear Programming by Quadratic approximation of the Lagrangian) • Quasi-Newton, Direct, sequential quadratic programming method • Like DFP, NLPQL – uses quadratic approximation of the function – Approximation formula for the Hessian called BFGS (Broyden-Fletcher-Goldfarb-Shanno) *Source: i. SIGHT online documentation

Results Overview • Objective function behavior (“mapping”) • 1 Parameter Optimization • 3 Parameter Optimization

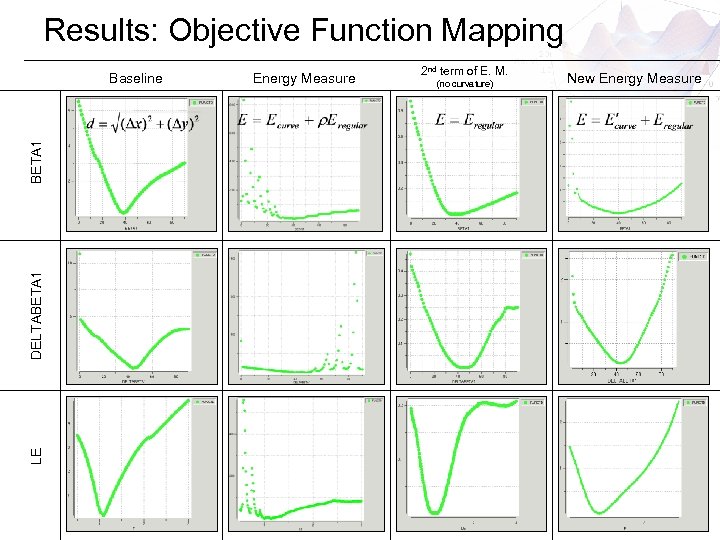
Results: Objective Function Mapping LE DELTABETA 1 Baseline Energy Measure 2 nd term of E. M. (no curvature) New Energy Measure

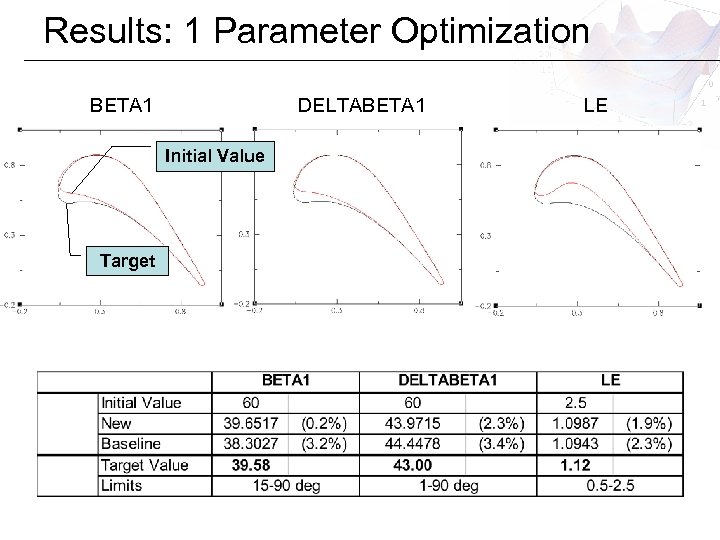
Results: 1 Parameter Optimization BETA 1 DELTABETA 1 Initial Value Target LE

Results: 3 Parameter Optimization Objective Functions New (Modified Energy Measure) Baseline Low Start High Start

Results: 3 Parameter Optimization (cont’d) Baseline objective function Low start High start Matched

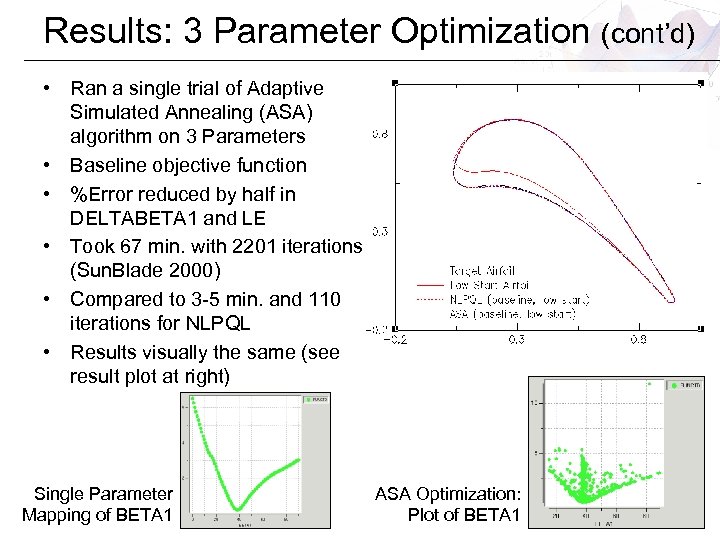
Results: 3 Parameter Optimization (cont’d) • Ran a single trial of Adaptive Simulated Annealing (ASA) algorithm on 3 Parameters • Baseline objective function • %Error reduced by half in DELTABETA 1 and LE • Took 67 min. with 2201 iterations (Sun. Blade 2000) • Compared to 3 -5 min. and 110 iterations for NLPQL • Results visually the same (see result plot at right) Single Parameter Mapping of BETA 1 ASA Optimization: Plot of BETA 1

Conclusions • Matching airfoil shapes through optimization is feasible • Quasi-Newton methods are fast and will work if objective function behaves smoothly • New objective function showed similar results to Baseline function with NLPQL optimizer • Improvements can be made to New function as design system discontinuities are fixed— curvature can be re-introduced to leading edge • 3 parameters: – BETA 1 is strongest parameter and achieves smallest %Error in final values – Visually close for both objective functions

Future Study • Required: – Complete in-house code and run comparative study to results of commercial code – Further trouble shooting of design system – Add curvature back into leading edge with cusps removed from model – Increase number of parameters to optimize – Determine how close is close enough • Possible: – Scaling parameters (BETA 1) or turn individual parameters off as they narrow in on target value – Consider other algorithms or combinations of algorithms – Limitations on achieving various target airfoil shapes

Acknowledgements • • • Dr. Hasan Akay, ME Department Ed Turner, Rolls-Royce mentor Larry Junod, Rolls-Royce mentor Dr. Steve Gegg, Rolls-Royce Dr. Asok Sen, Math Department

References • [1] Fletcher and Powell, A Rapidly Convergent Descent Method for Minimization, The Computer Journal, 1963, July • [2] Hamming, Richard W. , Introduction to Applied Numerical Analysis, Hemisphere Publishing Corp. , 1989 • [3] Arora, Jasbir S. , Introduction to Optimum Design, Elsevier Academic Press, 2004 • [4] Vanderplaats, Garret N. , Numerical Optimization Techniques for Engineering Design: With Applications, Mc. Graw Hill, Inc. , 1984 • [5] Cohen, I. , Ayache, N. , Sulger, P. , Tracking Points on Deformable Objects Using Curvature Information, Proceedings from the 2 nd European Conference on Computer Vision, 1992 • [6] Heath, M. , Scientific Computing: An Introductory Survey, 2 nd ed, Mc. Graw Hill, 2002 • [7] www. mathworks. com • [8] http: //nsr. bioeng. washington. edu/PLN/Members/butterw/JSIMDOC 1. 6/Contents. stx/User_Intro. stx • [9] i. SIGHT On-line documentation files