A Mathematical View of Our World 1 st

A Mathematical View of Our World 1 st ed. Parks, Musser, Trimpe, Maurer, and Maurer

Chapter 1 Numbers in Our Lives

Section 1. 1 ID Numbers and Check Digits • Goals • Study social security numbers • Study general identification numbers • Transmission errors • Check digits • Study universal product codes

1. 1 Initial Problem • Can you be confident that you will be charged the correct price if you purchase the item with this UPC? • The solution will be given at the end of the section.

Social Security Numbers • A social security number (SSN) is made up of: • A three-digit area number • A two-digit group number • A four-digit serial number

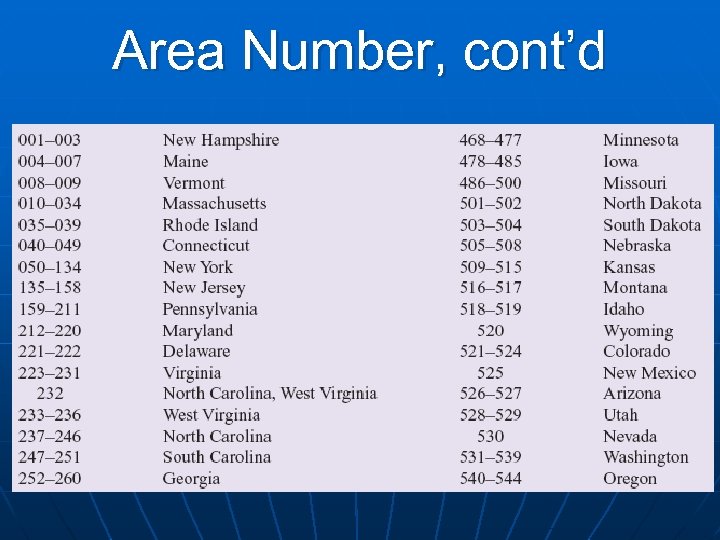
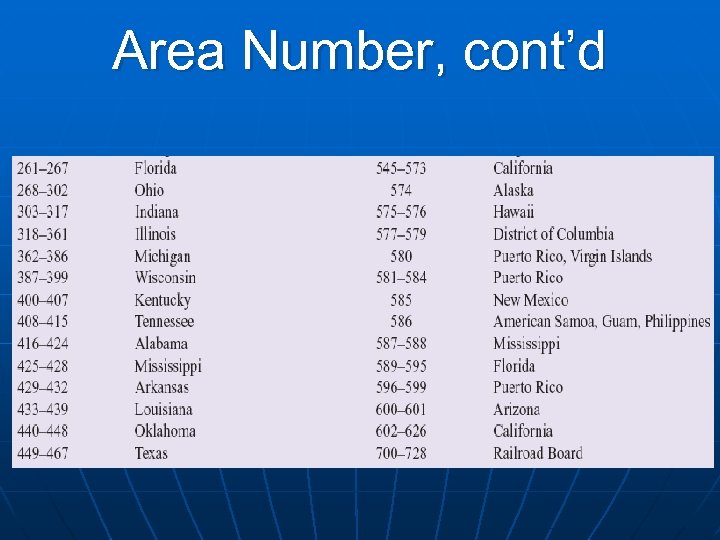
Area Number • XXX-XX-XXXX • Area numbers range from 001 – 728. • Before 1973, the area number depended on the state in which the office issuing the number was located. • Since 1973, the area number is determined by the mailing address of the applicant.

Area Number, cont’d

Area Number, cont’d

Group Number • XXX-XX-XXXX • Group numbers range from 01 – 99. • The group number groups together certain social security numbers. • The group number is not determined by any group to which a person belongs.

Group Number, cont’d • Group numbers are issued as follows: • First, odd numbers from 01 to 09. • Second, even numbers from 10 to 98. • Third, even numbers from 02 to 08. • Fourth, odd numbers from 11 to 99.

Serial Number • XXX-XX-XXXX • Serial numbers range from 0001 – 9999. • Serial numbers are issued in numerical order from smallest to largest.

Example 1 a) Which state was listed in the mailing address of the applicant who received the number 501 -92 -3287 ? b) Which number was issued first: 362 -13 -4158 or 362 -14 -9725 ?

Example 1, cont’d a) Solution: The area number in 501 -92 -3287 is 501. According to Table 1. 1, this social security number was issued to someone with a mailing address in North Dakota. b) Solution: The group number 14 is issued before the group number 13, so 362 -149725 was issued before 362 -13 -4158.

General ID Numbers • Many items besides people are assigned identification numbers. • For example: • International Standard Book Numbers (ISBN) for books • Vehicle Identification Numbers (VIN) for cars • Universal Product Codes (UPC) for grocery items

General ID Numbers, cont’d • Identification numbers are divided into two types: • Numeric ID numbers • Strings of digits • Alphanumeric ID numbers • Strings of digits, letters, and/or other symbols

General ID Numbers, cont’d • All digits, letters, or other symbols in an identification number are called characters. • The length of an identification number is the number of characters in the string. • Spaces, dashes, or other separators are not counted in the length of the string.

Question: A numeric identification number can contain: a. numbers only. b. letters and numbers only. c. letters, numbers, and other characters.

Example 2 • Determine the type and length of each ID number. a) SSN: 876 -87 -6543 b) ISBN: 0 -07 -231821 -X c) VIN: GHN 5 UC 265518 G d) UPC: 0 51000 01031 5

Example 2, cont’d • Solutions: a) The SSN 876 -87 -6543 is a numeric ID number of length 9. b) The ISBN 0 -07 -231821 -X is an alphanumeric ID number of length 10. c) The VIN GHN 5 UC 265518 G is an alphanumeric ID number of length 13. d) The UPC 0 51000 01031 5 is a numeric ID number of length 12.

Transmission Errors • An error in recording, reading, or relating an identification number is called a transmission error. • Two common ways in which transmission errors occur are replacement and transposition. • One character may accidentally be replaced by a different, incorrect, character. • Two adjacent characters may be interchanged.

Example 3 • What type of error occurred in each situation? a) The SSN 123 -45 -6789 was recorded as 123 -45 -6798. a) The SSN 123 -45 -6789 was recorded as 123 -45 -6788.

Example 3, cont’d • Solutions: a) The last two characters 89 were incorrectly written as 98. This is a transposition error. a) The last character 9 was incorrectly written as an 8. This is a replacement error.

Transmission Errors, cont’d • Suppose every possible ID number is a valid number in the identification system being used. • Any transmission errors in the number will result in the wrong person or item being identified. • It will not be evident that an error was made. • Most modern ID number systems are designed to guard against transmission errors.

Check Digits • Additional digits added to an identification number so that errors in transmission can be found are called check digits. • Ideally, a check-digit system should insure that any single-digit transmission error will result in an invalid ID number so that the error will be detected.

Question: Suppose a company assigns each employee a four-digit ID number in which the first three digits come from 0 through 9 and the last digit is a check digit chosen so that the sum of all four digits is divisible by 7. Fill in the missing digit in the ID number 3_82. a. 7 b. 5 c. 3 d. 1

Example 4 • Suppose a biology professor assigns a four-digit numeric ID number to each of the almost 1000 students in his class. • The first three digits are randomly assigned. • The fourth digit is the smallest number that makes the sum of all 4 digits divisible by 9.

Example 4, cont’d • If a replacement error is made in a single digit, it may be detected. • A 9 changed to a 0 or a 0 changed to a 9 will not be detected. • Other single-digit errors will be detected. • Transposition errors will not be detected. • Replacement errors in two or more digits may not be detected.

Example 5 • Suppose the professor from example 4 assigns a four-digit numeric ID number with the same check digit scheme, but using only the digits 0 – 8. • Any single-digit transmission error will be detected. • If a digit is changed to another digit from 0 – 8, the sum changes and is no longer divisible by 9. • If a digit is changed to a 9, it will be recognized as an invalid digit.

Universal Product Codes (UPC) • Almost every retail product has a 12 -digit numeric identification number, called a UPC, printed on its packaging. • Examples of UPCs are shown below.

UPCs, cont’d • The first digit, called the number system character, indicates the type of product.

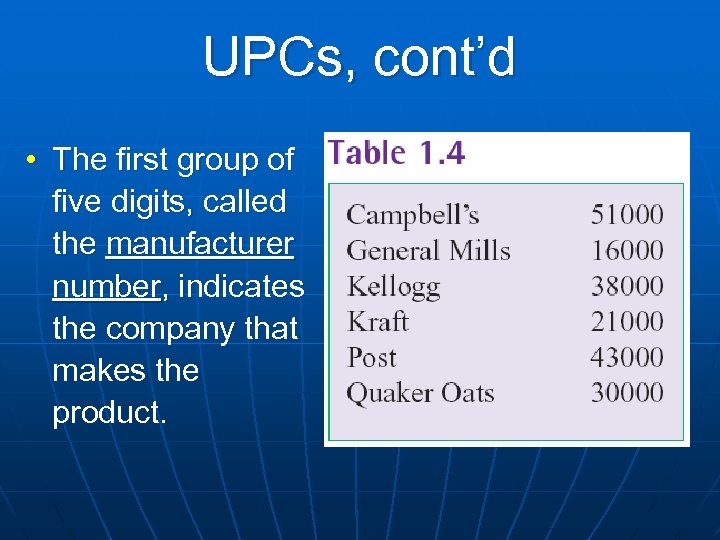UPCs, cont’d • The first group of five digits, called the manufacturer number, indicates the company that makes the product.

UPCs, cont’d • The second group of five digits, called the product number, indicates the specific product being sold. • Items sold by weight are not printed with product numbers. • Different manufacturers may use different or the same product numbers. There is no relationship between product numbers for various manufacturers.

UPCs, cont’d • The last digit is the check digit. • If the digits in a UPC are labeled as then the check digit is chosen so that the sum is divisible by 10.

UPCs, cont’d • The check-digit scheme for UPC numbers is a two-weight scheme. • The weights used are 3 and 1. • The sum is called a weighted sum.

Example 6 • Answer questions a – b about the chicken broth UPCs from the example earlier: 0 74785 00252 8 and 0 74785 50352 0. a) What is the number system character and what does it represent? • Solution: The number system character for both is 0 and it indicates that the chicken broth is a general grocery item.

Example 6, cont’d b) What is the manufacturer number and what does it represent? • Solution: The manufacturer number for both is 74785 and it indicates that the manufacturer is Valley Fresh Inc. (not given in the previous table of common manufacturers).

Example 6, cont’d c) What is the product number and what does it represent? • Solution: The product number for the can of clear broth is 00252. The product number for the can of fat free broth is 50352. • Two different products from the same company have two different product numbers.

Example 6, cont’d d) Verify that the check digits are correct. • Solution: For the can of clear broth, the calculation is: The weighted sum is divisible by 10, so the check digit is correct.

Example 6, cont’d • Solution: For the can of fat free broth, the calculation is: The weighted sum is divisible by 10, so the check digit is correct.

Example 7 • If the first 11 digits of a UPC are 2 13576 05341, what must the check digit be?

Example 7, cont’d • Solution: • Adding a 1 to 69 would make the weighted sum divisible by 10. The check digit must be a 1.

Example 8 • The first digit of a UPC is missing. If the remaining code is 01947 12513 3, what was the missing digit?

Example 8, cont’d • Solution: • The missing digit must be a 2, so that 6 + 64 = 70 will be divisible by 10.

1. 1 Initial Problem Solution • Can you be confident that you will be charged the correct price if you purchase the item with this UPC?

Initial Problem Solution, cont’d • The UPC is 2 26080 80291 8. • The initial digit of 2 indicates this item is sold by weight. • When the item was weighed a machine produced a label with the cost $2. 91 in positions 9 through 11 of the UPC. • The check digit is 8. Using the weighted sum check digit scheme will verify that this is correct. • The UPC is correct and you will be charged the right amount.

Section 1. 2 Modular Arithmetic and Check Digit Schemes • Goals • Study the division algorithm • Study congruence modulo m • Study modular check digit schemes

1. 2 Initial Problem • Suppose you want to buy a car. The vehicle identification number is 1 G 4 HP 54 C 5 KH 410030. • Is this number legitimate? • The solution will be given at the end of the section.

Numbers • Whole numbers are represented by the numerals 0, 1, 2, 3, 4, … • Integers are represented by the numerals …, -3, -2, -1, 0, 1, 2, 3, …

The Division Algorithm for Whole Numbers • The constants a and m must be whole numbers with m not equal to zero. • There are unique whole numbers q and r such that a = mq + r. • The constant r, the remainder, is less than m and greater than or equal to zero. • The constant a is the dividend, m is the divisor, and q is the quotient. • If r = 0, we say that m divides a or write m|a.

Example 1 • Use the division algorithm to find the quotient and remainder for the divisor 5 and the dividend 21.

Example 1, cont’d • Solution: We see that 21 = 5(4) + 1, so the quotient is q = 4 and the remainder is r = 1. • Since the remainder is not 0, 5 does not divide 21.

Example 2 • Use the division algorithm to find the quotient and remainder for the divisor 6 and the dividend 108.

Example 2, cont’d • Solution: We see that 108 = 6(18) + 0, so the quotient is q = 18 and the remainder is r = 0 • Since the remainder is 0, 6 divides 108.

Division Algorithm, cont’d • Many check digit schemes are based on using the division algorithm. • Usually it is the remainder from a division that is used as a check digit. • The quotient and remainder can be found by doing long division or by dividing on a calculator.

Division Algorithm, cont’d • To find the quotient and remainder for a whole number division using a calculator: 1) Perform the division a/m on the calculator. The whole number portion of the result is the quotient q. 2) Multiply the decimal portion of the result from Step 1 by the divisor m to get an approximation of the remainder r. 3) Round r to the nearest whole number to find the remainder.

Example 3 • Use a calculator to find the quotient and remainder for the divisor 13 and the dividend 543.

Example 3, cont’d • Solution: 1) Divide 543 by 13. The calculator shows a result of 41. 7692307692. The quotient is 41. 2) Multiply 0. 7692307692 by 13. The result is 9. 999996. 3) Round 9. 999996 to the nearest whole number to find the remainder. The remainder is 10. Check that 13(41) + 10 = 543.

Question: Find the quotient and remainder for the divisor 39 and the dividend 217. a. q = 22, r = 5 b. q = 0, r = 39 c. q = 5, r = 22 d. q = 3, r = 0

The Division Algorithm for Integers • The constants a and m must be integers with m greater than or equal to one. • There are unique integers q and r such that a = mq + r. • The constant r, the remainder, is less than m and greater than or equal to zero. • The constant a is the dividend, m is the divisor, and q is the quotient. • If r = 0, we say that m divides a or write m|a.

Division Algorithm, cont’d • To find the quotient and remainder for an integer division using a calculator: 1) Perform the division a/m on the calculator. • If the result is a whole number, the result is q. • If the result is not a whole number, q is the next smallest negative number.

Division Algorithm, cont’d • Cont’d: 2) Subtract q from the results from Step 1 and then multiply this value by the divisor m to get an approximation of the remainder r. 3) Round r to the nearest whole number to find the remainder.

Example 4 • Use a calculator to find the quotient and remainder for the divisor 7 and the dividend -359.

Example 4, cont’d • Solution: 1) Divide -359 by 7. The calculator shows a result of -51. 2857142857. The quotient is -52. 2) Subtract -52 from -51. 2857142857 to get 0. 7142857143. Multiply 0. 7142857143 by 7. The result is 5. 000001. 3) Round 5. 000001 to the nearest whole number to find the remainder. The remainder is 5. Check that 7(-52) + 5 = -359.

Congruence Modulo M • The constants a, b, and m must be integers with m greater than or equal to two. • Then if m evenly divides a – b, we say a is congruent to b modulo m. • The constant m is called the modulus, and the phrase modulo m is often shortened to mod m. • The definition above can be written symbolically as follows:

Question: Choose the number below that is NOT congruent to 85 mod 3. a. 52 b. 55 c. 62 d. 64

Example 5 • Verify each of the congruencies. a) • Solution: 66 – 38 = 28 = 4(7). Since the difference of the two integers is a multiple of 7, they are congruent mod 7. b) • Solution: 3422 – -153 = 3575 = 275(13). The two integers are congruent mod 13.

Modular Arithmetic • Let modulus m > 0 be a fixed integer. The numbers a, b, and c are integers. • Modular arithmetic has the following rules: 1) 2) 3)

Modular Arithmetic, cont’d 4) 5) 6) • Where k is any positive integer

Modular Check Digit Schemes • Common choices of a modulus for check digit schemes are 7, 9, 10, and 11. • Modular check digit schemes follow this pattern: • If necessary, replace each non-numeric character with a digit according to a standard code.

Modular Check Digit Schemes • Cont’d: • Treat the string as a whole number or combine the digits in some type of weighted sum. • The check digit is the whole number r between 0 and m – 1 that is congruent mod m to the number from step 2. If a check digit is greater than 9, it must be replaced by an alphanumeric character.

A Mod 9 Check Digit Scheme • An ID number has k + 1 digits, where k is some positive integer: • The check digit, which is the last digit, is the whole number from 0 to 8 that is congruent modulo 9 to the number made up of the first k digits.

Example 6 • A company uses a mod 9 check digit scheme for 5 -digit ID numbers. What is the check digit for 5368?

Example 6, cont’d • Solution: Calculate 5368/9 = 596. 44444. • Multiply 0. 44444 by 9 to get 3. 999996. • The remainder, which is the check digit, is 4. The complete ID number is 53684.

Mod 9 Check Digit Scheme, cont’d • The check digit in this type of scheme can also be found through the shortcut of casting out nines. • Add the first k digits of the ID number. • This sum must be congruent modulo 9 to the check digit • Example: 5+3+6+8 = 22, which is congruent to 4 mod 9. The check digit is again found to be 4.

Example 7 • A company uses a mod 9 check digit scheme for 5 -digit ID numbers. What is the missing digit in the smudged number?

Example 7, cont’d • Solution: Call the missing digit X. The ID number is 73 X 11. Using the procedure of casting out nines we find that 7 + 3 + X + 1 = 11 + X must be congruent mod 9 to the check digit 1. We see that 11 + 8 = 19, which is 1 more than a multiple of 9. The missing digit X must be 8. • The ID number is 73811.

Example 8 • A U. S. Post Office money order has an 11 digit ID number with a mod 9 check digit scheme. • If a money order has an ID number of 2995709918 what is the check digit that should go in the 11 th place in the string?

Example 8, cont’d • Solution: 2995709918 is congruent mod 9 to its check digit. The sum of its digits is 2 + 9 + 5 + 7 + 0 + 9 + 1 + 8 = 59, which is congruent to 5 mod 9. • The check digit is 5. • The entire ID number for the money order is 29957099185.

Example 9 • Euro banknotes use a check digit scheme in which the check digit is chosen so that the entire serial number is divisible by 9. • The code is alphanumeric, with values assigned to the letters as shown in the next slide.

Example 9, cont’d

Example 9, cont’d • Suppose a 20 -euro banknote has a serial number of S 07090546498 • Verify that the serial number is correct.

Example 9, cont’d • Solution: The serial number is S 07090546498. The character S has a value of 2. • The serial number is worth 207090546498. • The sum of its digits is 2 + 0 + 7 + 0 + 9 + 0 + 5 + 4 + 6 + 4 + 9 + 8 = 54, which is congruent to 0 mod 9.

A Mod 7 Check Digit Scheme • An ID number has k + 1 digits, where k is some positive integer: • The check digit, which is the last digit, is the whole number from 0 to 6 that is congruent modulo 7 to the number made up of the first k digits.

Example 10 • An airline ticket has an ID number with a mod 7 check digit scheme. • Verify that the number located in the bottom center of the ticket below is a valid ID number.

Example 10, cont’d • Solution: The ID number is equal to 1615042694252. • For the ID number to be valid, the number made of the first 12 digits must be congruent to 2 mod 7. • Check that 7 divides (161504269425 – 2) = 161504269423, so the congruency holds and the number is valid.

A Mod 11 Check Digit Scheme • A check digit scheme for VINs uses congruence modulo 11. • A VIN is a 17 -digit alphanumeric ID number with values assigned to the characters according to the table below.

Mod 11 Check Digit Scheme, cont’d • The check digit is the 9 th character. A check digit of 10 is represented by X. A weighted sum is used with weights of 8, 7, 6, 5, 4, 3, 2, 10, 9, 8, 7, 6, 5, 4, 3, and 2 for the characters.

1. 2 Initial Problem Solution • The car’s VIN is 1 G 4 HP 54 C 5 KH 410030. Is this number legitimate? • The digit 5 in the 9 th position is the check digit. • Convert each letter to a digit. • The 16 digits, without the check digit, are 17487543 28410030.

Initial Problem Solution, cont’d • Calculate the weighted sum: 8(1) + 7(7) + 6(4) + 5(8) + 4(7) + 3(5) + 2(4) + 10(3) + 9(2) + 8(8) + 7(4) + 6(1) + 5(0) + 4(0) + 3(3) + 2(0) = 327. • If the VIN is valid, 327 must be congruent modulo 11 to the check digit 5. However, this is not the case. • The VIN is not valid. Do not buy the car.

Section 1. 3 Encoding Data • Goals • Study binary codes • Morse code • UPC bar codes • Braille code • ASCII • Postnet code

1. 3 Initial Problem • The envelope below has been damaged. Use the Postnet bar code to determine the ZIP+4 code. • The solution will be given at the end of the section.

Binary Codes • Coding methods are used to encode numbers and other data before they are transmitted. • A data coding system made up of two states or symbols is called a binary code.

Binary Codes, cont’d • Many common coding systems are binary codes. • Morse code • UPC bar codes • Braille code • ASCII • Postnet code

Morse Code • In Morse code, each character is encoded using dots and dashes. • Morse code is a binary code because it was developed for telegraphs which have two states, ON and OFF. • The code is created by leaving the telegraph circuit ON or OFF for a certain length of time.

Morse Code, cont’d • The circuit is ON for one unit of time to create a dot. • The circuit is ON for three units of time to create a dash. • The circuit is OFF for one unit of time between any dots or dashes in a character.

Morse Code, cont’d • The circuit is OFF for three units of time between characters. • The circuit is OFF for six units of time between words.

Morse Code, cont’d • The codes for each character are shown below.

Example 1 • The Morse code for the word “MATH” is illustrated in the figure below. • ON is represented by a black square and OFF by a white square.

Morse Code, cont’d • ON and OFF can also be represented by the binary digits 0 and 1. • ON is represented by 1. • OFF is represented by 0. • Example: The letter A can be encoded using 0 s and 1 s as shown below.

Morse Code, cont’d

Example 2 • Convert the message “MATH” to Morse code using 0 s and 1 s.

Example 2, cont’d • Solution: • M is encoded as 1110111 • A is encoded as 10111 • T is encoded as 111 • H is encoded as 1010101 • A 0 is inserted between each character. • The coded message is 11100010111000101.

Example 3 • Convert the Morse code message “ 10100010100000011100010100010111010001” to English. • Recall that the code 000 separates characters, while 000000 separates words.

Example 3, cont’d • Solution: The first word is 101000101. • 1010101 = H • 000 = break between characters • 101 = I • The first word is HI.

Example 3, cont’d • The second word is 11100010100010111010001 • 111 = T • 000 = break between characters • 1010101 = H • 1=E • 1011101 = R • 1=E • The decoded message is HI THERE

Question: Translate the message “SMILE” into Morse code. a. 101010111010111010101 b. 101010001110001011101010001 c. 10101000000111000000101110 1010000001 d. 101010001110001011101010001 01110101

UPC Bar Codes • Universal Product Code (UPC) numbers on retail items are encoded using a binary code. • The encoding is represented by vertical bars. • The bars are easily read by the laser scanner.

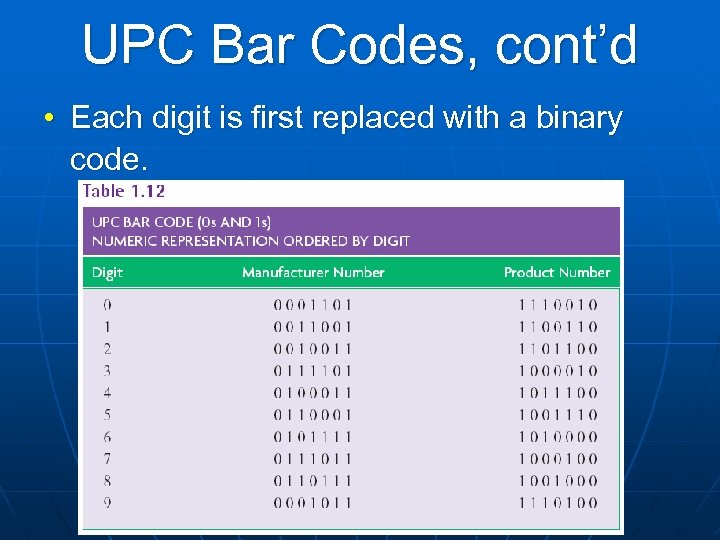UPC Bar Codes, cont’d • Each digit is first replaced with a binary code.

Question: Does the UPC binary code below represent a manufacturer number or a product number? 10100001011101000 a. manufacturer number b. product number c. impossible to determine

UPC Bar Codes, cont’d • Similarly to Morse code, each 0 is represented by a white bar and each 1 by a black bar.

Example 4 • Convert the manufacturer number 365 into a sequence of 0 s and 1 s.

Example 4, cont’d • Solution: • The digit 3 is encoded as 0111101. • The digit 6 is encoded as 0101111. • The digit 5 is encoded as 0110001. • The encoding is 011110101011110110001.

Example 5 • Convert the manufacturer number 365 into a bar code.

Example 5, cont’d • Solution: The individual bar codes for 3, 6, and 5 are found in the table.

Example 5, cont’d • Solution, cont’d: The individual bar codes are placed in order from left to right, and then scaled to look like a UPC.

UPC Bar Codes cont’d • The laser scanner at the store must be able to read: • In which direction a bar code is scanned • Where a bar code begins and ends • Various widths of bars used on different products.

UPC Bar Codes cont’d • Every UPC bar code begins and ends with a guard bar pattern. • The pattern consists of a white strip between two black strips, all the same width. • The width of each strip is called a module and is the unit of width for that particular bar code.

UPC Bar Codes cont’d • Every UPC bar code also has a center bar pattern. • The pattern consists of five alternating strips, starting with white. • Each strip is one module wide.

UPC Bar Codes cont’d • A bar code from a can of Campbell’s Cream of Chicken Soup is shown below.

Example 6 • Check this bar code for Campbell’s Cream of Chicken Soup. The manufacturer number is 51000 and the product number is 01031. • Recall that a UPC consists of a single digit, followed by the manufacturer number, the product number, and finally a check digit. • For general grocery items the initial digit is 0.

Example 6, cont’d • Solution: The first 11 digits of the UPC number are 05100001031. The check digit, d, must be found. • We know that the weighted sum 3(0 + 1 + 0 + 0 + 1) + 1(5 + 0 + 1 + 3 + d) must be a multiple of 10. So 6 + 9 + d = 15 + d indicates that d must be a 5. • The UPC number is 051000010315.

Example 6, cont’d • Solution cont’d: The bar code for the UPC 051000010315 must be created. • A guard bar pattern begins the code. • The bar code for each digit in the manufacturer number and the product number follows. • Recall that the center bar pattern goes between the manufacturer and product codes. • A guard bar pattern ends the code.

Example 6, cont’d • Solution cont’d: The bar code is shown below, in its initial state and its final scaled version.

Example 6, cont’d • Solution cont’d: Compare our bar code for the soup to a bar code from an actual can of soup.

Braille Code • The Braille system of writing is a binary code. • Every Braille symbol is a pattern of 6 dots, each of which is raised or not raised.

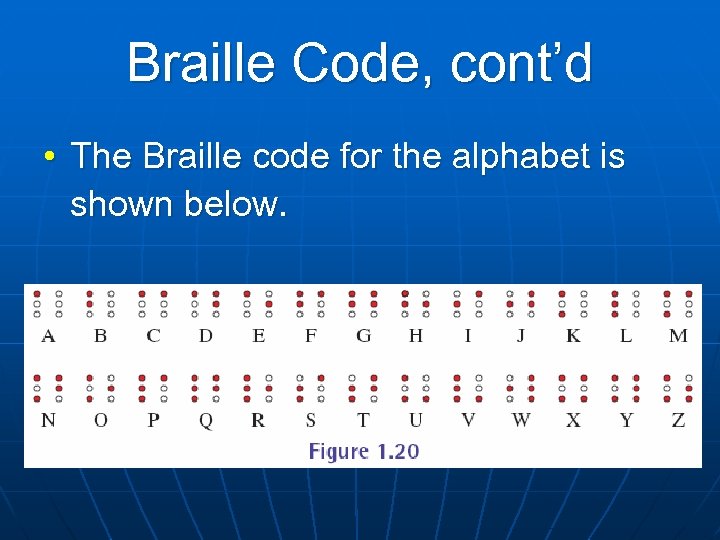Braille Code, cont’d • The Braille code for the alphabet is shown below.

Example 7 • Decode the Braille message shown below.

Example 7, cont’d • Solution: Find each character in the Braille alphabet. • The message is decoded as NEVERMORE.

ASCII • The American Standard Code for Information Interchange (ASCII) is used by most computers. • ASCII is pronounced “ask-key”. • Each character is encoded using 8 binary digits, called a byte.

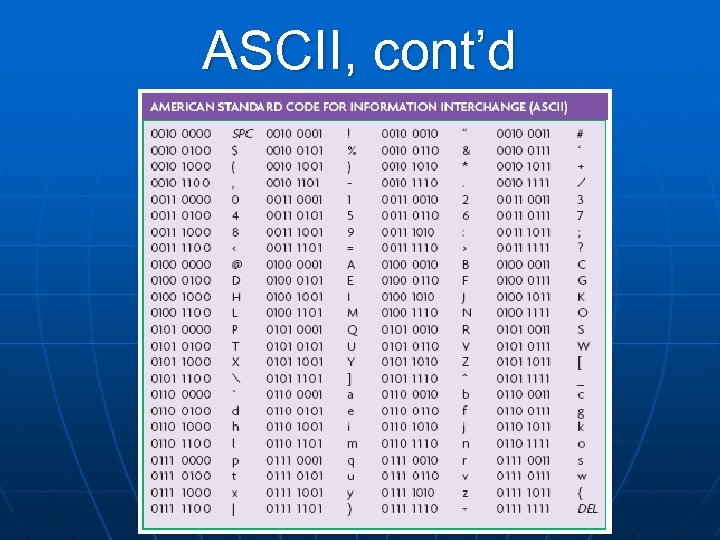ASCII, cont’d

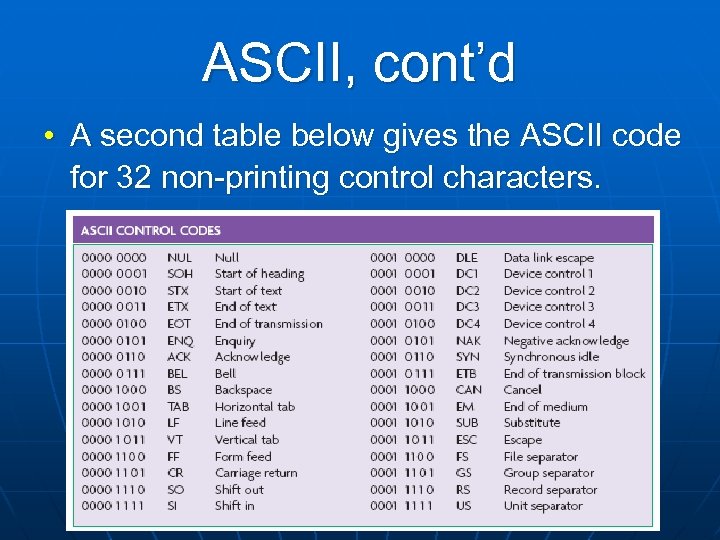ASCII, cont’d • A second table below gives the ASCII code for 32 non-printing control characters.

Example 8 • Convert the message from ASCII to English. • 01001000101 01001100 01001111.

Example 8, cont’d • Solution: • 01001000 = H • 01000101 = E • 01001100 = L • There are two of these. • 01001111 = E • The message reads HELLO.

Postnet Code • The U. S. Postal Service uses a code called Postnet to encode ZIP codes as bars. • Postnet encodes • 9 -digit ZIP+4 codes used on business reply forms • 11 -digit ZIP+4 plus delivery-point code used on reduced-rate business mail. • A delivery-point code consists of the last two digits of the street address or box number.

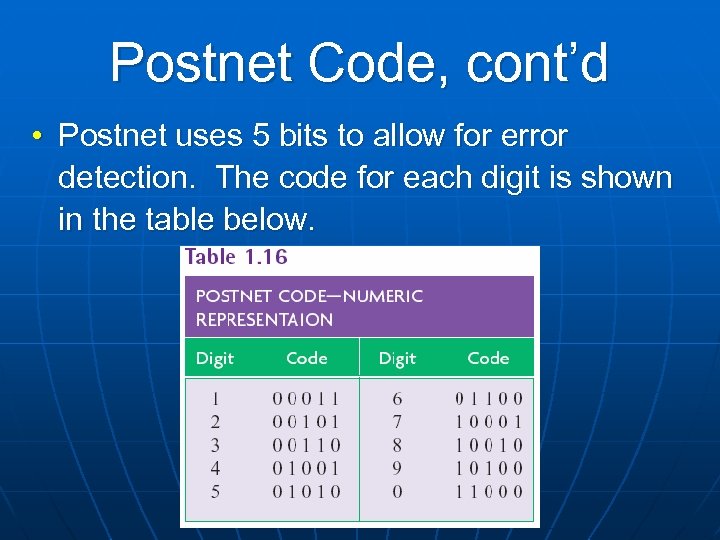Postnet Code, cont’d • Postnet uses 5 bits to allow for error detection. The code for each digit is shown in the table below.

Postnet Code, cont’d • On pieces of mail, the Postnet code is represented as a series of bars. • The 1 s are represented by tall bars. • The 0 s are represented by short bars. • The Postnet bar codes are shown below.

Postnet Code, cont’d • Complete Postnet codes include: • Guard bars, consisting of a single tall bar on each end. • An extra check digit before the last guard bar. • The check digit is chosen so that the sum of all the digits is divisible by 10.

1. 3 Initial Problem Solution • The envelope below has been damaged. Use the Postnet bar code to determine the ZIP+4 code.

Initial Problem Solution, cont’d • Each set of 5 bars inside the guard bars represents a digit. Compare the code on the envelope to the decoding table.

Initial Problem Solution, cont’d • The final 0 is the check digit. The ZIP+4 code is 80323 -8510.