A linear time algorithm for the weighted lexicographic

A linear time algorithm for the weighted lexicographic rectilinear 1 -center problem in the plane Nir Halman, Technion, Israel This work is part of my Ph. D. thesis, held in Tel Aviv University, under the supervision of Professor Arie Tamir

Planar 1 -center problems Input: a set P={p 1, …, pn} of n points pi=(xi, yi) a set W={w 1, …, wn} of positive weights Output: a center p=(x, y) which minimizes f(p)=Maxi {wi d(p, pi )} where d is a distance function Motivation: customers, service center, 1/wi =speed d=l 2: solvable in linear time [M 83], [D 86], [SW 96]

Rectilinear 1 -center (d=l 1 ) c = Minp Maxi {wi (|xi-x|+|yi-y|)} Min c s. t. wi (|xi-x|+|yi-y|) c, Min i=1, …, n c s. t. wi ((xi-x)+(yi-y)) c, i=1, …, n, wi (-(xi-x)+(yi-y)) c, i=1, …, n, wi ((xi-x)-(yi-y)) c, i=1, …, n, wi (-(xi-x)-(yi-y)) c, i=1, …, n. Transform the problem into one where d=l

1 -center problem with d=l c = Minp Maxi {wi Max{|xi-x|, |yi-y|}} Min c wi|xi-x| c, i=1, …, n, wi|yi-y| c, s. t. i=1, …, n. Decomposition into 2 one-dimensional problems Min cx s. t. wi|xi-x| cx i=1, …, n. c=Max{cx , cy} Min cy s. t. wi|yi-y| cy i=1, …, n.

Lex 1 -center problem [O 97] Unique solutions to 1 -dimensional problems and Euclidean planer 1 -center This is not the case for planar 1 -center with l 1 , l Input: a set P={p 1, …, pn} of n points pi=(xi, yi) a set W={w 1, …, wn} of positive weights Output: a center p=(x, y) which lex-minimizes lf(p)=q(w 1 d(p, p 1 ), …, wn d(p, pn )) where q is the non-decreasing ordering of a multi-set

Example Y p 3=(3, 2) p 1=(-4, 1) p 5=(5, 0) X p 2=(6, -1) p 4=(2, -3) The distances vector is lf(p)=(5, 5, 4, 2½) No O(n log n) time algorithm exists

Talk outline • Introduction • An (n log n) lower bound for calculating the optimal value of the optimal solution • A restricted problem, the min rays problem and the relations between them • Solving the min rays problem in linear time • Putting it all together

Lower bound Obs 1: it takes (n log n) time to compute the distances vector of a given set of n real points Proof: reduction from sorting Given is a set R={r 1, …, rn} of n real numbers Suppose the minimal element is 0 Set P={r 1, …, rn , 2 rmax} Center is rmax Distances vector yields sorting of R

Talk outline • Introduction • An (n log n) lower bound for calculating the optimal value of the optimal solution • A restricted problem, the min rays problem and the relations between them • Solving the min rays problem in linear time • Putting it all together

Restricted problem Input: P={p 1, …, pn}, W={w 1, …, wn} as before and a real number x@ Output: a center p@ =(x@, y) which lex-minimizes lf(p@)=q(w 1 d(p@, p 1 ), …, wn d(p@, pn )) Set ai = wi|x@- xi|, gi(y)=max{ai, wi|y-yi|}, then lf(p@)=q(g 1(y), …, gn(y )) Obs 2: Each gi(y) has a shape

Min rays problem gi(y) define r-i(y) as and r+i(y) as Let u(y) be upper envelop of {r-i(y), r+i(y) | i=1, …, n} Goal: calculate c = min u(y) + r- Y p 3=(3, 2) p 1=(-4, 1) p 5=(5, 0) X r r -2 1 r+ 5 r+ 2 C r -4 r -3 1 r+ 4 r+ 3 p 2=(6, -1) p 4=(2, -3) Y

Restricted vs. min rays Thm 1: y$, c$ an optimal solution of the min rays problem (x@, y$) is an optimal center in the corresponding restricted problem Proof: C C Y Y

Talk outline • Introduction • An (n log n) lower bound for calculating the optimal value of the optimal solution • A restricted problem, the min rays problem and the relations between them • Solving the min rays problem in linear time • Putting it all together

Solving min rays problem Let y$, c$ be an optimal solution of the min rays problem, p@=(x@, y$) be an optimal center for the corresponding restricted problem. Oracle: Input: same as for min rays problem with an additional point p =(x@, y) Output: y$=y or y$>y, or y$

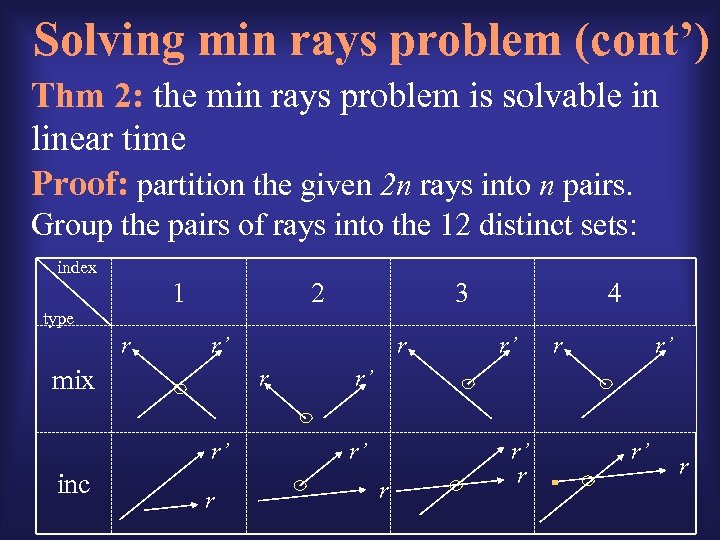Solving min rays problem (cont’) Thm 2: the min rays problem is solvable in linear time Proof: partition the given 2 n rays into n pairs. Group the pairs of rays into the 12 distinct sets: index 1 2 3 4 type r r’ mix r r’ inc r r r’ r’ r’ r

Solving min rays problem (cont’) Proof (cont’): r’ ½ of the rays are dropped r r r’ ¼ of rays are dropped r’ r 1/ 8 of rays are dropped

Talk outline • Introduction • An (n log n) lower bound for calculating the optimal value of the optimal solution • A restricted problem, the min rays problem and the relations between them • Solving the min rays problem in linear time • Putting it all together

Putting it all together Algorithm: • transform the input to l • solve non-lex problem • solve min rays problem Generalizes to (in the same time bound): • lex 1 -center in Rd with l norm (quadratic dependency in d ) • different weights on each of the axes • all centers

Thank you !