A Linear Lower Bound on the Communication Complexity

A Linear Lower Bound on the Communication Complexity of Single-Server PIR Iftach Haitner Jonathan Hoch Weizmann Institute of Science Israel Gil Segev

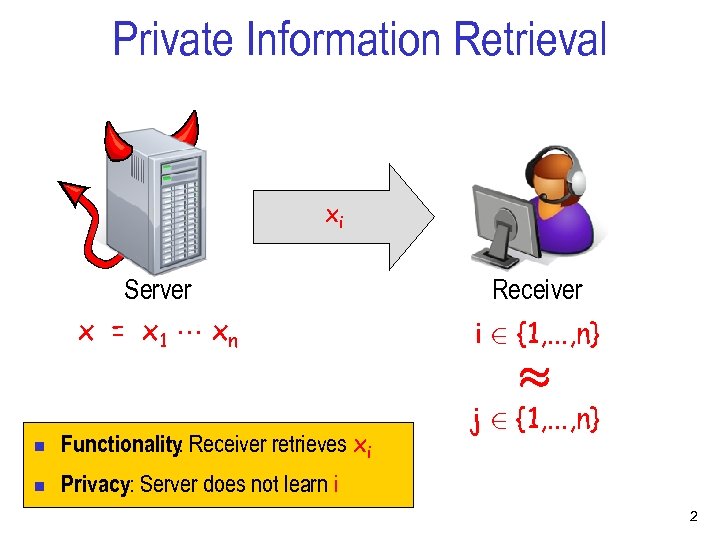
Private Information Retrieval xi Server x = x 1 xn Receiver i 2 {1, . . . , n} ¼ n Functionality Receiver retrieves xi : n j 2 {1, . . . , n} Privacy: Server does not learn i 2

Not information theoretically [CGKS] The Trivial Solution Can we do better than trivial? x 1 xn Server x = x 1 xn n Receiver i 2 {1, . . . , n} Inefficient -- x may be very large 3

Two Approaches n Multiple-server PIR n n n Information theoretic privacy Many exciting results, but not the focus of this talk Single-server PIR n n [CGKS 95, . . . , Yek 07, . . . ] [CG 97, KO 97, CMS 99, . . . ] Computational privacy Implies Oblivious Transfer 2 -message PIR implies collision-resistant hash functions and publickey encryption Many applications. . . 4

Current Status n Specific number-theoretic assumptions n n [KO 97, CMS 99, . . . ] Communication polylog(n) General assumptions n n [KO 00] Communication n - o(n) Black-box construction based on TDPs Question: Can we base single-server PIR with sublinear communicationon general assumptions? 5

Main Result In any fully black-box construction of single-server PIR for an n-bit database from trapdoor permutations over (n) bits, the server sends (n) bits. n Two restrictions n n Fully black-box Tight security reduction: permutations over (n) bits [KO ‘ 00]: (n²) bits n Previous results n n [Fis 02]: Similar result for 2 -message protocols (less restrictions) [HHRS 07]: (n/logn) lower bound (same restrictions) (n²) lower bound for “not so tight” reductions 6

Fully Black-Box Reductions A fully black-box reduction from to A: B Black-box construction n n Any implementation of A implies an implementation of B Only care about the functionality of A Black-box proof of security n n Any adversary for B implies an adversary for A Only care about functionality of the adversary for B Adversary for A B A A Adversary for B 7

Our Approach n Fully black-box reductions relativize n We present an oracle O relative to which: 1. There exists a collection of TDPs over {0, 1}n n A random function is hard to invert even with access to O 2. There is no single-server PIR protocol for an n-bit database in which the server sends o(n) bits n There exists an efficient server that uses O to break any such protocol 8

The Oracle [HHRS ‘ 07] n n n O = (Sam, ) is a random collection of TDPs over {0, 1}n Sam is an interactive collision-finding oracle n n Samples random collisions Extends the non-interactive oracle of [Simon ‘ 98] v 0 Ã {0, 1}n C 1(v 1) = C 1(v 0) C 2(v 2) = C 2(v 1) A v 0 Sam C 1 v 1 C 2 v 2 9

The Oracle [HHRS ‘ 07] n n n O = (Sam, ) is a random collection of TDPs over {0, 1}n Sam is an interactive collision-finding oracle n n Samples random collisions Extends the non-interactive oracle of [Simon ‘ 98] A Theorem: A random TDP is one-way as long as Sam answers queries of depth · n/log(n) n n The proof requires additional restrictions (Ci+1 refines Ci, commit to Ci+1 at depth i, . . . ). . . but this suffices for the purpose of this talk v 0 Sam C 1 v 1 n/log(n) C 2 v 2 10

Breaking 2 -Message PIR a(i) b(a, x) x = x 1 xn i 2 {1, . . . , n} 11

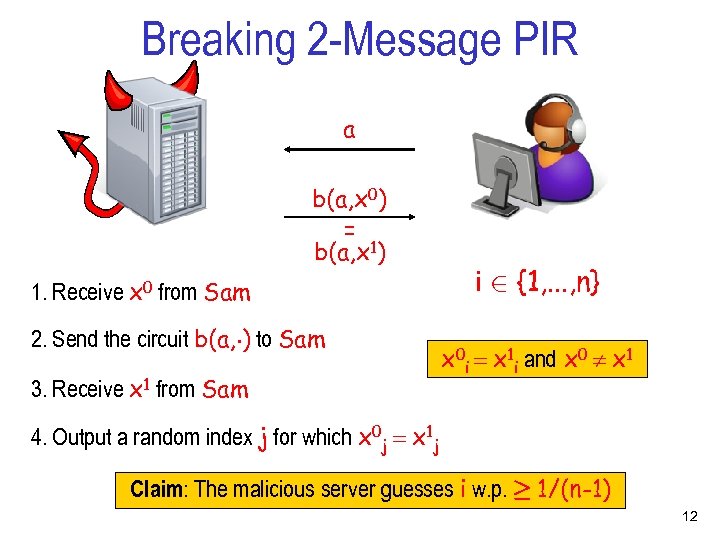
Breaking 2 -Message PIR a b(a, x 0) = b(a, x 1) 1. Receive x 0 from Sam 2. Send the circuit b(a, ¢) to Sam 3. Receive x 1 from Sam i 2 {1, . . . , n} x 0 i = x 1 i and x 0 x 1 4. Output a random index j for which x 0 j = x 1 j Claim: The malicious server guesses i w. p. ¸ 1/(n-1) 12

Breaking Any Sublinear PIR a 1 . . . b 1 ao(n) bo(n) i 2 {1, . . . , n} Communication vs. Rounds: Server sends o(n) bits ) o(n) rounds, server sends one bit each round 13

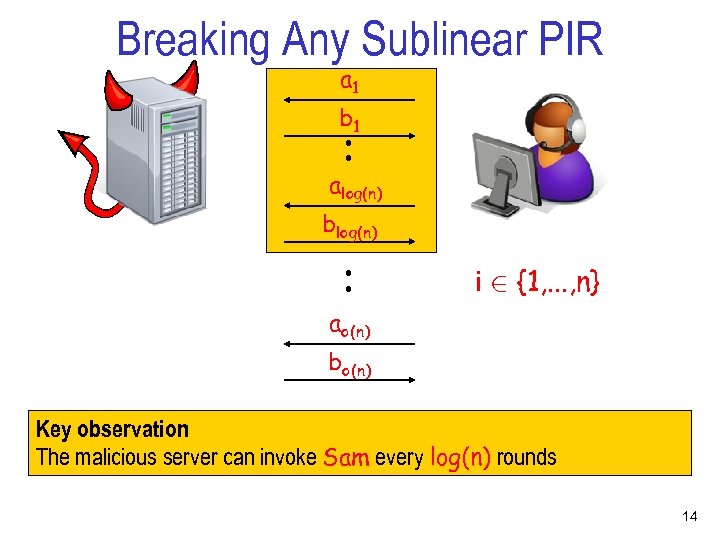
Breaking Any Sublinear PIR a 1 . . b 1 alog(n) . . blog(n) i 2 {1, . . . , n} ao(n) bo(n) Key observation : The malicious server can invoke Sam every log(n) rounds 14

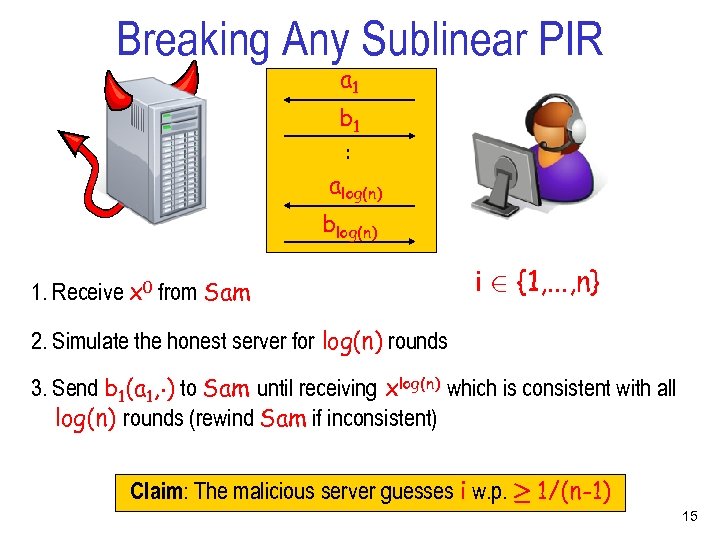
Breaking Any Sublinear PIR a 1 . . b 1 alog(n) blog(n) 1. Receive x 0 from Sam i 2 {1, . . . , n} 2. Simulate the honest server for log(n) rounds 3. Send b 1(a 1, ¢) to Sam until receiving xlog(n) which is consistent with all log(n) rounds (rewind Sam if inconsistent) Claim: The malicious server guesses i w. p. ¸ 1/(n-1) 15

Summary n Communication lower bound for single-server PIR n n n In the paper: n n Fully black-box constructions from (enhanced) TDPs The trivial solution is optimal up to constant factors Matches the upper bound of [NOVY] Communication lower bound for statistically-hiding bit-commitment The sender must send (n) bits Communication preserving reduction to single-server PIR Open problem: n n A linear lower bound for “not so tight” reductions? [KO ‘ 00]: TDPs over (n²) bits Thank you! 16