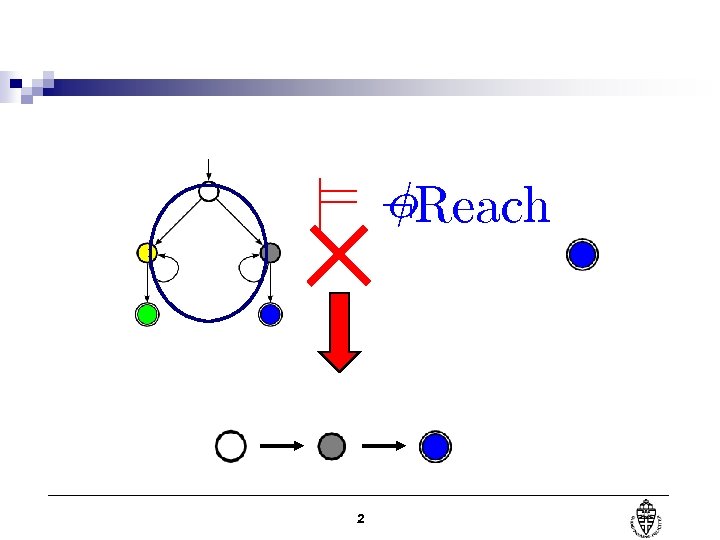
 Á j= : Reach 2
Á j= : Reach 2
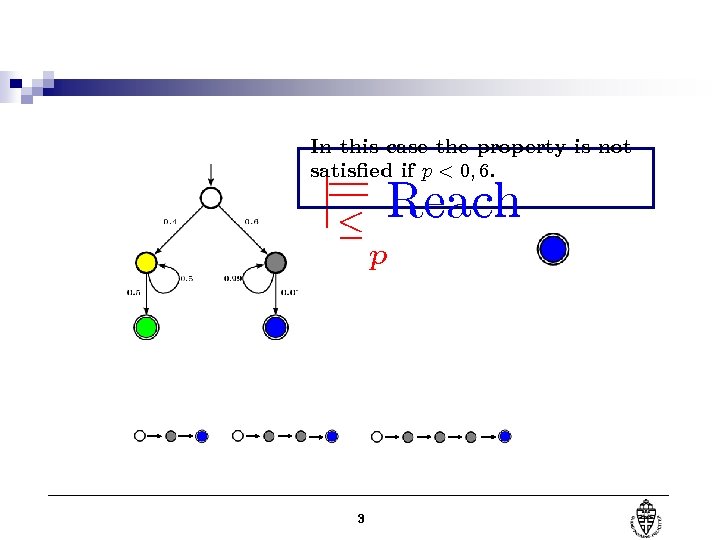 In this case the property is not satis¯ed if p < 0; 6. j= Reach · p 3
In this case the property is not satis¯ed if p < 0; 6. j= Reach · p 3
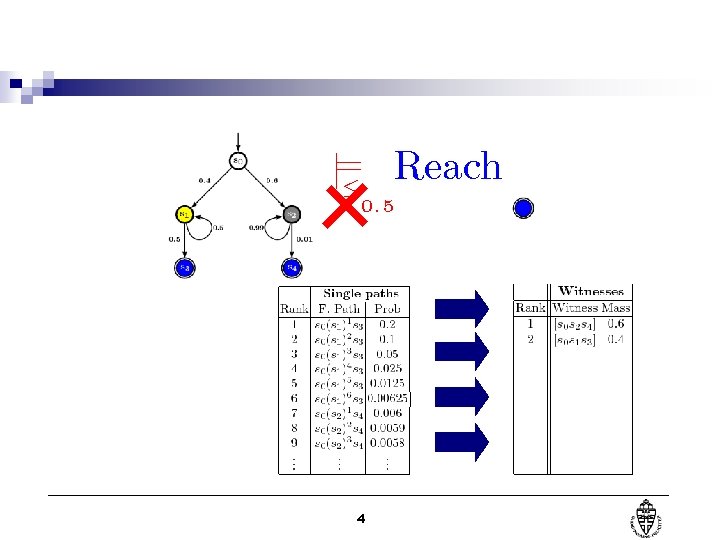 j= Reach · 0: 5 4
j= Reach · 0: 5 4
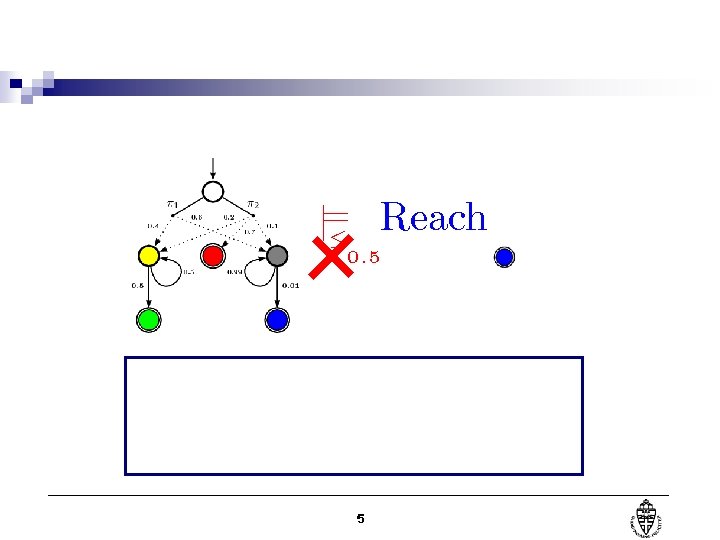 j= Reach · 0: 5 5
j= Reach · 0: 5 5
 6
6
 7
7
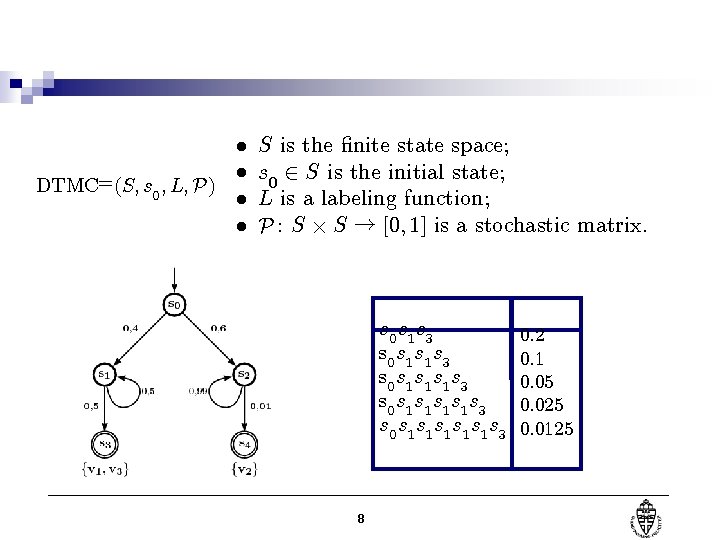 ² ² DTMC=(S; s 0 ; L; P ) ² ² S is the ¯nite state space; s 0 2 S is the initial state; L is a labeling function; P : S £ S ! [0; 1] is a stochastic matrix. s 0 s 1 s 3 s 0 s 1 s 1 s 1 s 1 s 3 8 0. 2 0. 1 0. 05 0. 025 0. 0125
² ² DTMC=(S; s 0 ; L; P ) ² ² S is the ¯nite state space; s 0 2 S is the initial state; L is a labeling function; P : S £ S ! [0; 1] is a stochastic matrix. s 0 s 1 s 3 s 0 s 1 s 1 s 1 s 1 s 3 8 0. 2 0. 1 0. 05 0. 025 0. 0125
 Á : : = V j : Á j Á ^ Á j ÁU Á _; !; §; and ¤ are syntactic sugar ¾ ¾ j= D v : Á Á^° ÁU ° , , v 2 L(¾ 0 ) not(¾ j= Á) D ¾ j= Á and ¾ j= ° D D ¸ : ¾# = ° and 9 i 0 i j. D 80·j; ¸g ²Sat(Á) , f¾ 2 Paths(D) j ¾ j= Ág
Á : : = V j : Á j Á ^ Á j ÁU Á _; !; §; and ¤ are syntactic sugar ¾ ¾ j= D v : Á Á^° ÁU ° , , v 2 L(¾ 0 ) not(¾ j= Á) D ¾ j= Á and ¾ j= ° D D ¸ : ¾# = ° and 9 i 0 i j. D 80·j; ¸g ²Sat(Á) , f¾ 2 Paths(D) j ¾ j= Ág
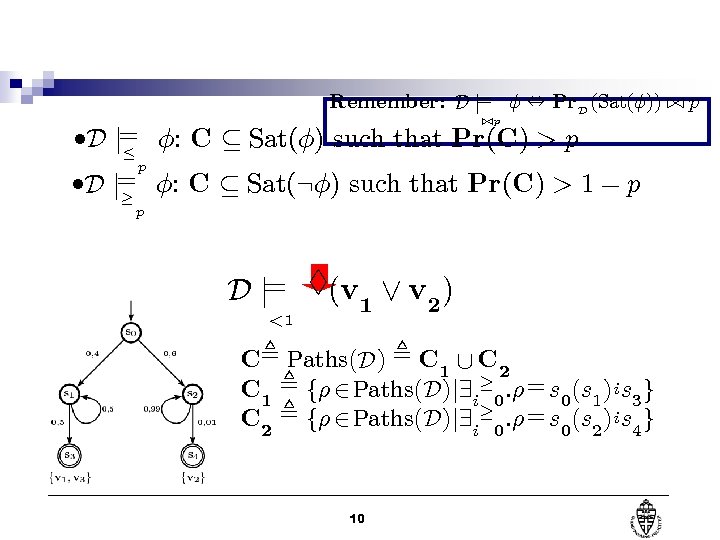 Remember: D j= Á , Pr. D (Sat(Á)). / p. /p ²D j= Á: C µ Sat(Á) such that Pr(C) > p · p ²D j= Á: C µ Sat(: Á) such that Pr(C) > 1 ¡ p ¸ p D j= §(v 1 _ v 2 ) <1 C, Paths(D ) , C 1 [ C 2 C 1 , f½ 2 Paths(D )j 9 i¸ 0 : ½ = s 0 (s 1 )i s 3 g C 2 , f½ 2 Paths(D )j 9 i¸ 0 : ½ = s 0 (s 2 )i s 4 g 10
Remember: D j= Á , Pr. D (Sat(Á)). / p. /p ²D j= Á: C µ Sat(Á) such that Pr(C) > p · p ²D j= Á: C µ Sat(: Á) such that Pr(C) > 1 ¡ p ¸ p D j= §(v 1 _ v 2 ) <1 C, Paths(D ) , C 1 [ C 2 C 1 , f½ 2 Paths(D )j 9 i¸ 0 : ½ = s 0 (s 1 )i s 3 g C 2 , f½ 2 Paths(D )j 9 i¸ 0 : ½ = s 0 (s 2 )i s 4 g 10
 11
11
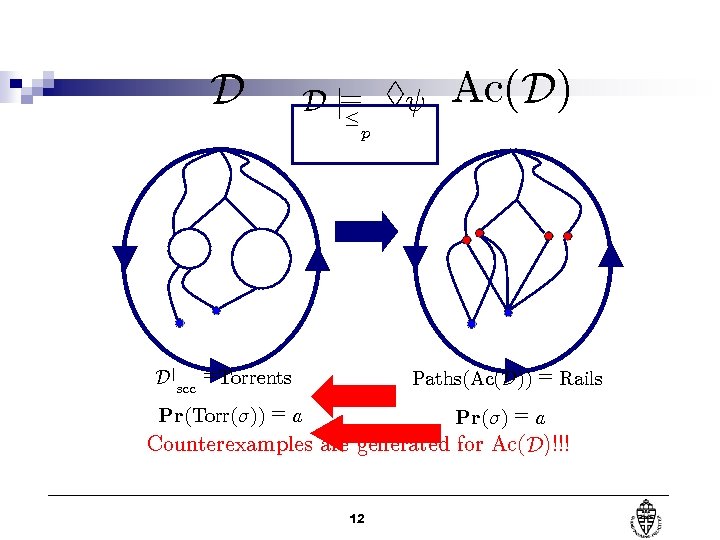 D D j= §Ã · Ac(D) p Djscc =Torrents Paths(Ac(D)) = Rails Pr(Torr(¾)) = a Pr(¾) = a Counterexamples are generated for Ac(D )!!! 12
D D j= §Ã · Ac(D) p Djscc =Torrents Paths(Ac(D)) = Rails Pr(Torr(¾)) = a Pr(¾) = a Counterexamples are generated for Ac(D )!!! 12
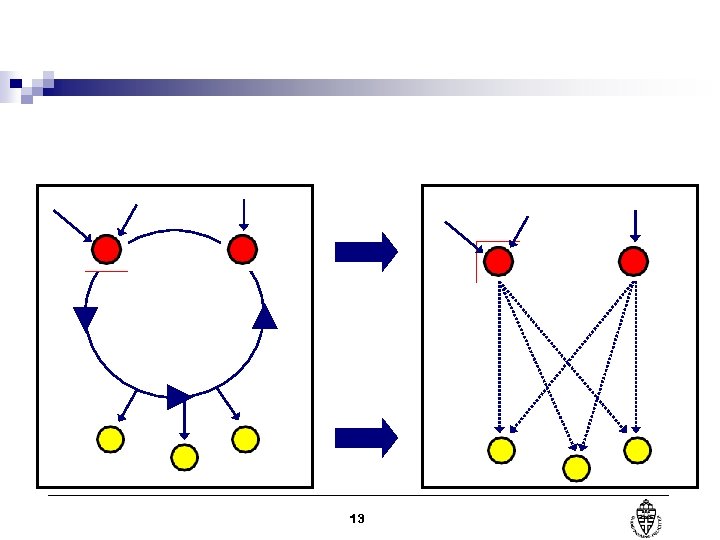 13
13
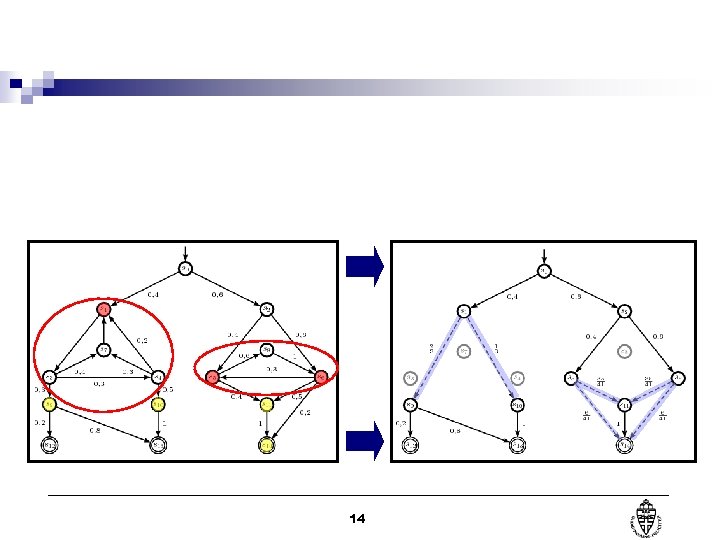 14
14
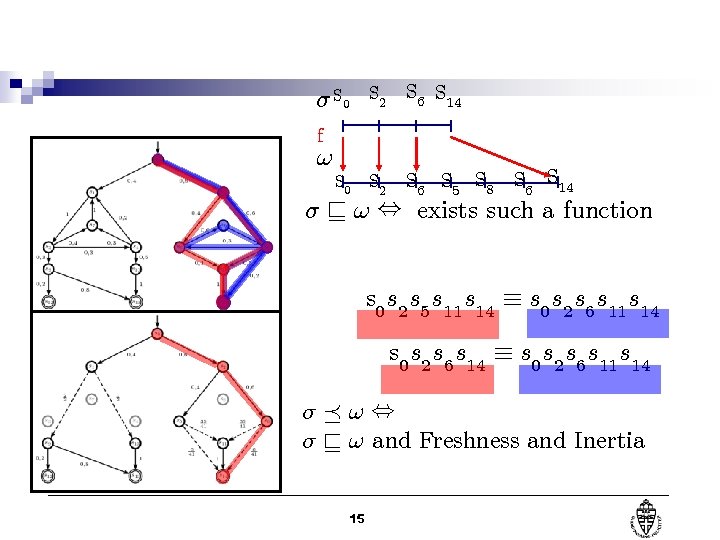 ¾ S 0 S 2 S 6 S 14 S 2 S 6 S 5 S 8 f ! S 0 S 6 S 14 ¾ v ! , exists such a function s 0 s 2 s 5 s 11 s 14 ´ s 0 s 2 s 6 s 11 s 14 s 0 s 2 s 6 s 14 ´ s 0 s 2 s 6 s 11 s 14 ¾¹!, ¾ v ! and Freshness and Inertia 15
¾ S 0 S 2 S 6 S 14 S 2 S 6 S 5 S 8 f ! S 0 S 6 S 14 ¾ v ! , exists such a function s 0 s 2 s 5 s 11 s 14 ´ s 0 s 2 s 6 s 11 s 14 s 0 s 2 s 6 s 14 ´ s 0 s 2 s 6 s 11 s 14 ¾¹!, ¾ v ! and Freshness and Inertia 15
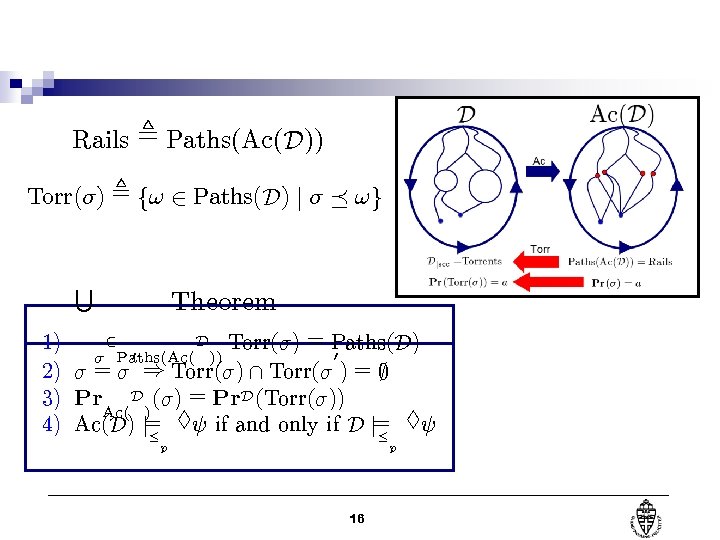 Rails , Paths(Ac(D )) Torr(¾) , f! 2 Paths(D) j ¾ ¹ !g S Theorem 2 D Torr(¾) = Paths(D ) 1) 0 0 ¾ Paths(Ac( )) = ¾ ) Torr(¾) Torr(¾ ) = ; 2) ¾ 3) Pr D (¾) = Pr. D (Torr(¾)) Ac( ) 4) Ac(D ) j= §Ã if and only if D j= §Ã · · p p 16
Rails , Paths(Ac(D )) Torr(¾) , f! 2 Paths(D) j ¾ ¹ !g S Theorem 2 D Torr(¾) = Paths(D ) 1) 0 0 ¾ Paths(Ac( )) = ¾ ) Torr(¾) Torr(¾ ) = ; 2) ¾ 3) Pr D (¾) = Pr. D (Torr(¾)) Ac( ) 4) Ac(D ) j= §Ã if and only if D j= §Ã · · p p 16
 17
17
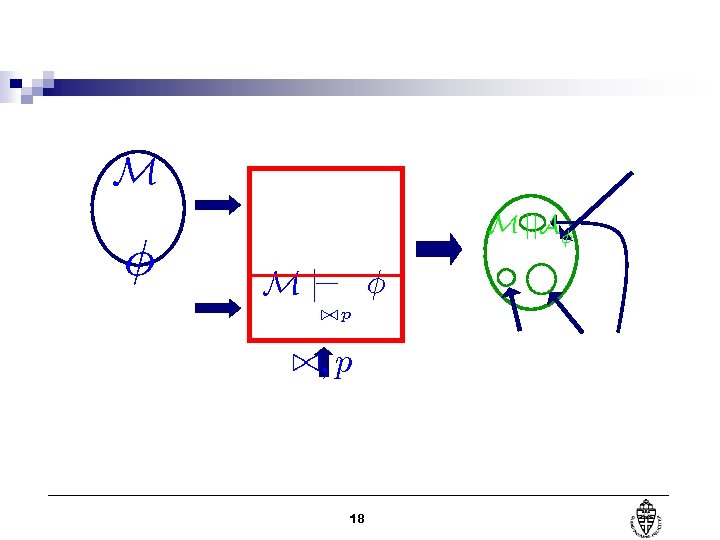 M Á M jj. AÁ M j= Á. /p . /; p 18
M Á M jj. AÁ M j= Á. /p . /; p 18
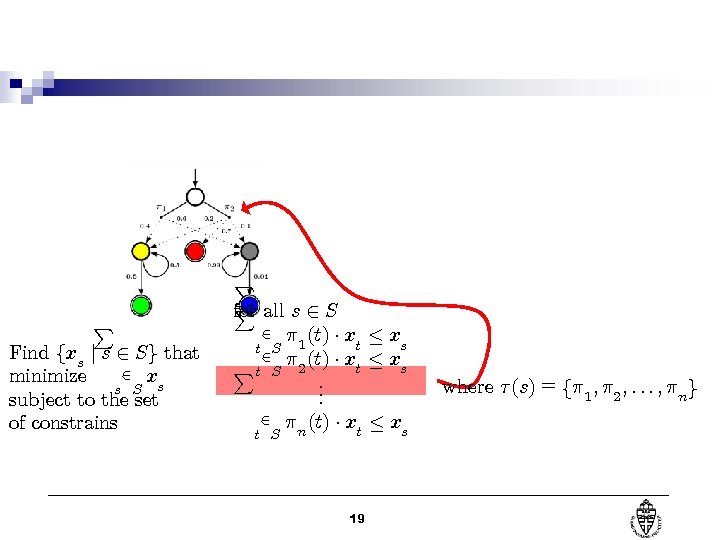 P Find fxs j s 2 S g that 2 x minimize s S s subject to the set of constrains P P for all s 2 S 2 ¼ (t) ¢ x · x t s t S 1 2 ¼ (t) ¢ x · x s t P t S 2. . . 2 ¼ (t) ¢ x · x n s t t S 19 where ¿ (s) = f¼ 1 ; ¼ 2 ; : : : ; ¼n g
P Find fxs j s 2 S g that 2 x minimize s S s subject to the set of constrains P P for all s 2 S 2 ¼ (t) ¢ x · x t s t S 1 2 ¼ (t) ¢ x · x s t P t S 2. . . 2 ¼ (t) ¢ x · x n s t t S 19 where ¿ (s) = f¼ 1 ; ¼ 2 ; : : : ; ¼n g
 0 M j= §Ã , M j= §Ã · · p p 0 C is a counterexample to M j= §Ã · p + C is a counterexample to M j= §Ã · p 20
0 M j= §Ã , M j= §Ã · · p p 0 C is a counterexample to M j= §Ã · p + C is a counterexample to M j= §Ã · p 20
 21
21
 22
22
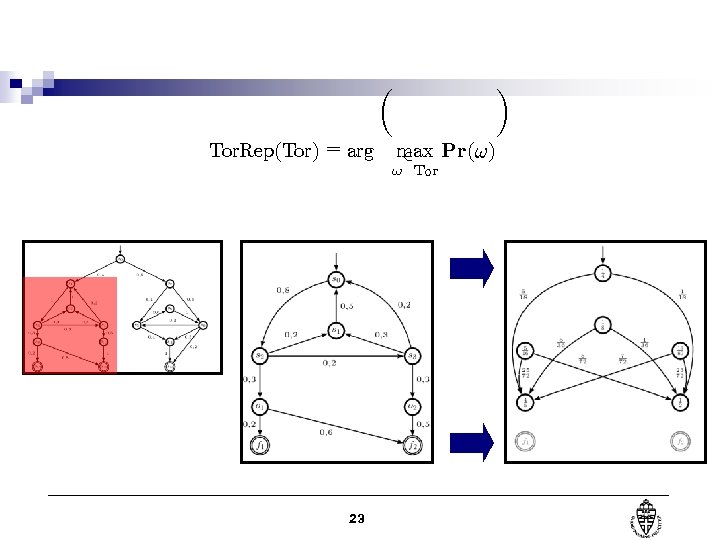 µ Tor. Rep(Tor) = arg ¶ max Pr(!) 2 ! Tor 23
µ Tor. Rep(Tor) = arg ¶ max Pr(!) 2 ! Tor 23
 24
24
 25
25
 26
26
 27
27