A High Performance Shared Information Space Model for

A High Performance Shared Information Space Model for Parallel Scientific Applications Li Zhang and Manish Parashar The Applied Software Systems Laboratory ECE/CAIP, Rutgers University http: //www. caip. rutgers. edu/TASSL (Ack: NSF, Do. E, NIH, Do. D)

High Performance Adaptive & Interactive Simulations • High performance simulations have become critical research modalities in science and engineering • Large-scale, knowledge-based, data-driven, adaptive and interactive simulations can enable accurate solutions to realistic models of complex phenomena – Complex/sophisticated numerical techniques – Adaptive: resolution, algorithms, execution, scheduling, … – Interactive: peer interactions between computations and users, data, resources, instruments … • Key components include – Conceptual and numerical models – Computational and computer science – Information and infrastructure

Computational Modeling of Physical Phenomena • Realistic, physically accurate computational modeling – Large computation requirements – Dynamic and complex couplings • multi-physics, multi-model, multi-resolution, …. – Dynamic and complex interactions • application, application resource, application data, application user, … – Software/systems engineering/programmability • volume and complexity of code, community of developers, … – scores of models, hundreds of components, millions of lines of code, …

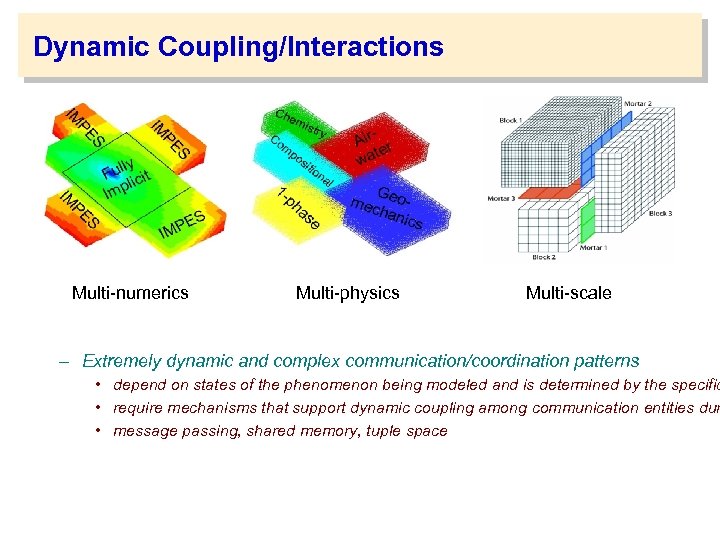Dynamic Coupling/Interactions Multi-numerics Multi-physics Multi-scale – Extremely dynamic and complex communication/coordination patterns • depend on states of the phenomenon being modeled and is determined by the specific • require mechanisms that support dynamic coupling among communication entities dur • message passing, shared memory, tuple space

IPARS Multiphysics Motivation (M. Peszynska) Goal: Use most efficient and at the same time appropriate physical model to simulate a given phenomenon in a part of the computational domain. Example: Two phase oil flow under IPARS can be simulated using one of 3 models: two phase sequential, implicit, or black oil code run in two-phase. They differ dramatically in complexity. Solution: Use multi-block type grid, apply appropriate models where necessary and couple them across interface.

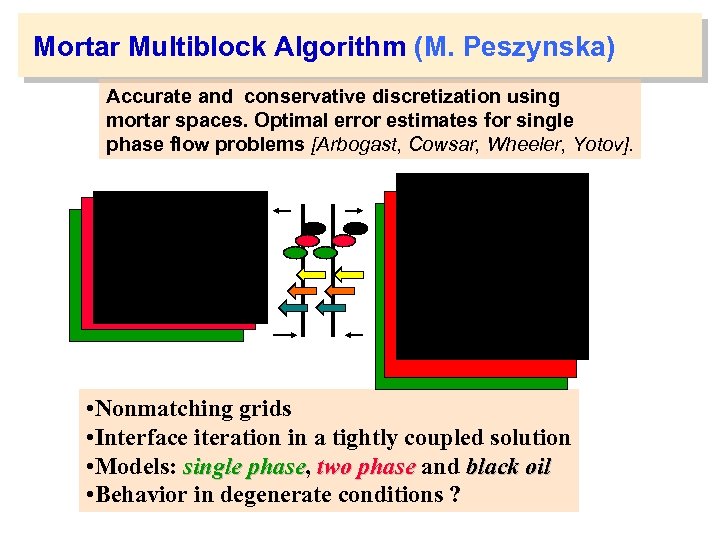Mortar Multiblock Algorithm (M. Peszynska) Accurate and conservative discretization using mortar spaces. Optimal error estimates for single phase flow problems [Arbogast, Cowsar, Wheeler, Yotov]. • Nonmatching grids • Interface iteration in a tightly coupled solution • Models: single phase, two phase and black oil phase • Behavior in degenerate conditions ?

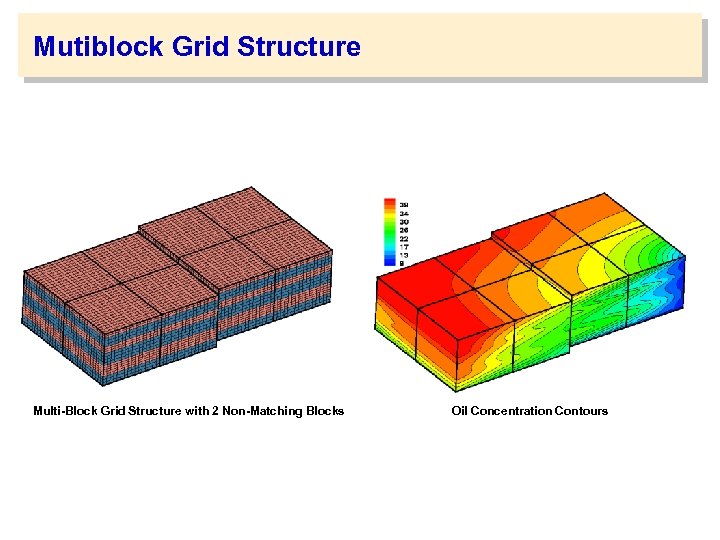Mutiblock Grid Structure Multi-Block Grid Structure with 2 Non-Matching Blocks Oil Concentration Contours

Interactions in Scientific Simulations • Geometry-based Problem Domain – Formulations of most scientific and engineering applications are based on geometric multi-dimensional domains, e. g. , grid or mesh. • Local Interactions/Communication – Interactions in these applications are typically between entities that are geometrically close in this domain (e. g. , neighboring cells, nodes or elements).

High Performance Shared Information Space (SEINE) • SEINE – Dynamic geometry-based shared space model • Key Features – exploit locality of communication into realized scalable shared spaces – shared spaces dynamically created/destroyed – associative geometry-based sharing semantics – support dynamic communication/coordination patterns

SEINE: Geometry-based Sharing • Objects are associated with regions in a geometrically defined space – e. g. , the grid or mesh • Shared spaces are dynamically defined on processors associated with the region of sharing – region can grow and shrink • Objects can be associatively read/written from/to the shared space – “get” and “put” operators semantically/functionally similar to “in” and “out” in Linda. • Assumptions • Each geometry-based to be shared in the space is required to first register with SEINE system before it is put/get to/from the shared space.

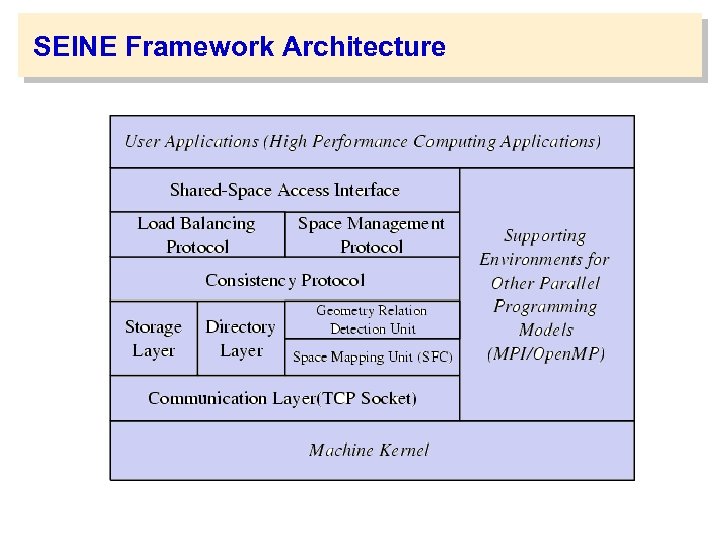SEINE Framework Architecture

SEINE Framework Architecture • Distributed directory layer – efficient object registration and lookup based geometric relationship among regions of interaction • dynamic (hierarchical) geometry-based distributed index space • Storage layer – spans a dynamic set of nodes based on the geometric relationships of their regions of interaction – shared space storage is physically replicated on each of the participating nodes.

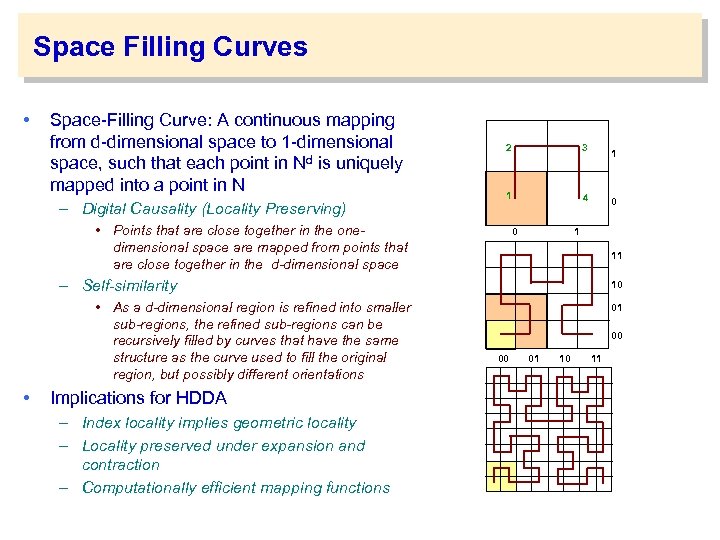Space Filling Curves • Space-Filling Curve: A continuous mapping from d-dimensional space to 1 -dimensional space, such that each point in Nd is uniquely mapped into a point in N – Digital Causality (Locality Preserving) 2 3 1 4 • Points that are close together in the onedimensional space are mapped from points that are close together in the d-dimensional space 0 1 11 – Self-similarity • As a d-dimensional region is refined into smaller sub-regions, the refined sub-regions can be recursively filled by curves that have the same structure as the curve used to fill the original region, but possibly different orientations • Implications for HDDA – Index locality implies geometric locality – Locality preserved under expansion and contraction – Computationally efficient mapping functions 10 01 00 00 01 10 11

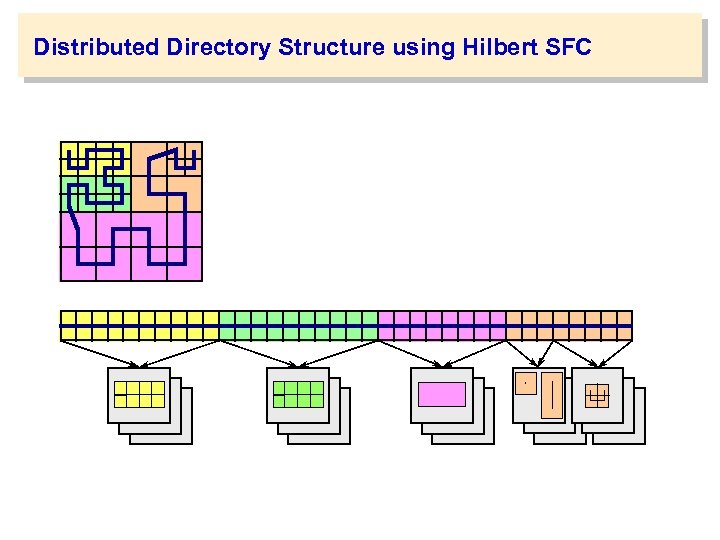Distributed Directory Structure using Hilbert SFC

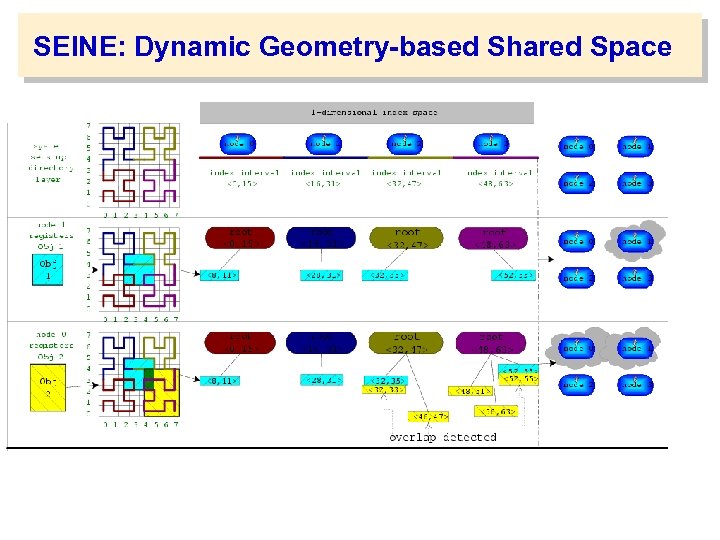SEINE: Dynamic Geometry-based Shared Space

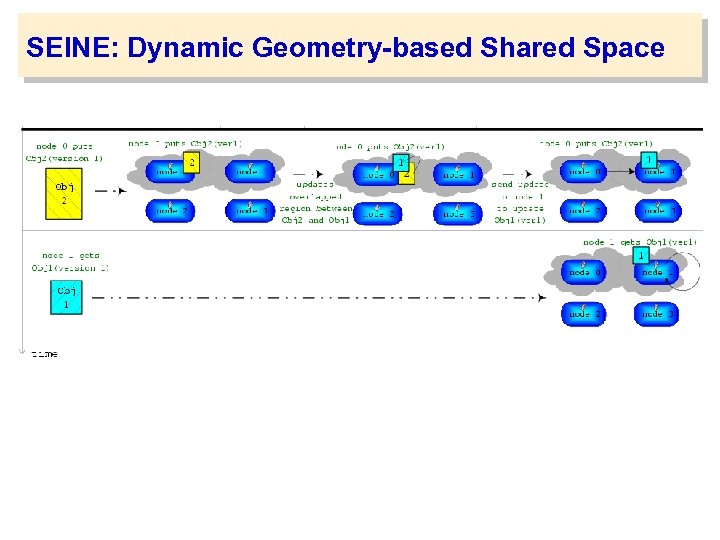SEINE: Dynamic Geometry-based Shared Space

SEINE Framework (cont. ) • Shared space consistency – update propagation + multiple versioning – assumption: nodes only access their registered objects • Load balancing – Load balancing at space creation/object registration • the directory layer is constructed by evenly dividing the 1 -D index space into equal intervals and assigned them to nodes – Load balancing during object sharing • load balancing depends on application load-balancing • workload on each node is directly related to the number of objects the node has registered

SEINE Interface – seine* Register(object geometry description) • Registers an object with SEINE. Based on passed geometric information, a pointer pointed to an existing SEINE or to a new SEINE will be returned. Several transient spaces may be merged upon a new object’s join action. – int Put(object geometry description, data, version#) • Moves an object from requesting node to a SEINE. – int Get(object geometry description, data, version#) • Moves an object from a SEINE to requesting node. Further • “get” requests on the object are blocked until it is “put” back to SEINE. – int Read(object geometry description, data, version#) • Copies an object to requesting node without removing it • from SEINE. Multiple “read” operations can occur simultaneously. – int De-register(object geometry description) • De-registers an object with SEINE. A space may be decomposed into several disconnected spaces upon an object’s de-register action.

Experimental Evaluation • A Prototype Implementation – Using multithreading, TCP sockets – Complements MPI, Open. MP, … • Test application – multiblock oil-reservoir simulation based on IPARS

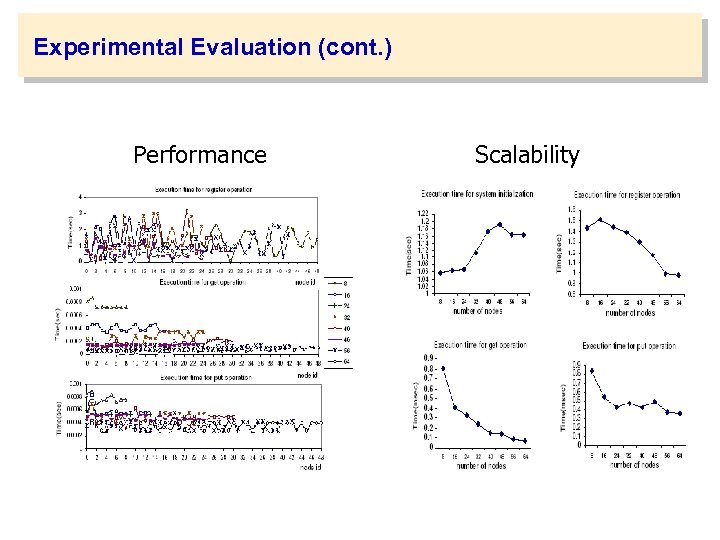Experimental Evaluation (cont. ) Performance Scalability

Conclusion • Adaptive and interactive simulations can enable accurate solutions of physically realistic models of complex phenomenon – efficient implementation presents challenges • A key challenge is the extremely dynamic and complex communication/coordination patterns – depend on states of the phenomenon being modeled and is determined by the specific numerical formulation, domain decomposition and/or sub-domain refinement algorithms used, and are known only at runtime • SEINE Framework – supports scalable geometry-based distributed shared spaces – enables decoupled associated interactions – complemetns MPI, Open. MP, … • Other applications – Mx. N mappings, scientific code coupling, load-balancing, etc.