A General Decomposition for Reversible Logic Year 2001

A General Decomposition for Reversible Logic Year 2001 M. Perkowski, L. Jozwiak#, P. Kerntopf+, A. Mishchenko, A. Al-Rabadi, A. Coppola@, A. Buller*, X. Song, M. Md. Mozammel Huq Azad Khan&, S. Yanushkevich^, V. Shmerko^, M. Chrzanowska-Jeske Portland State University, Portland, Oregon 97207 -0751 #Technical University o f Eindhoven, The Netherlands, + Technical University of Warsaw, Poland, @ Cypress Semiconductor Northwest and Oregon Graduate Institute, Oregon, USA , * Information Sciences Division, Advanced Telecommunications Research Institute International (ATR), Kyoto, Japan, & Department of Computer Science and Engineering, East West University, Bangladesh, , ^ Technical University of Szczecin, Poland

Atom-scale computation: • What are the difficulties in trying to build a classical computing machine on such a small scale? • One of the biggest problems with the program of miniaturizing conventional computers is the difficulty of dissipated heat. • As early as 1961 Landauer studied the physical limitations placed on computation by heat dissipation.

Computing at the atomic scale: a survey made by Keyes in 1988 R. W. Keyes, IBM J. Res. Develop. 32, 24 (1988). • Plot showing the number of dopant impurities involved in logic with bipolar transistors with year. – (Copyright 1988 by International Business Machines Corporation, reprinted with permission. )

Information loss = energy loss • The loss of information is associated with laws of physics requiring that one bit of information lost dissipates k T ln 2 of energy, where k is Boltzmann’ constant and T is the temperature of the system. • Interest in reversible computation arises from the desire to reduce heat dissipation, thereby allowing: – higher densities – speed R. Landauer, “Fundamental Physical Limitations of the Computational Process”, Ann. N. Y. Acad. Sci, 426, 162(1985).

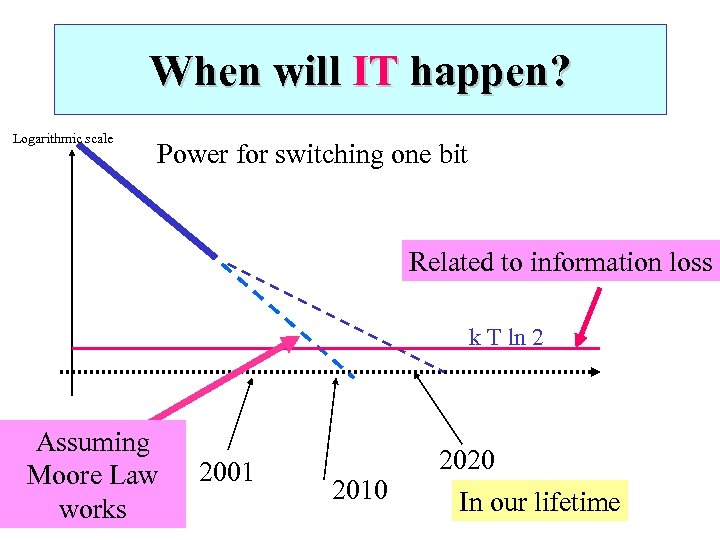
When will IT happen? Logarithmic scale Power for switching one bit Related to information loss k T ln 2 Assuming Moore Law works 2001 2010 2020 In our lifetime

Reversible Logic • Bennett showed that for power not be dissipated in the circuit it is necessary that arbitrary circuit can be build from reversible gates.

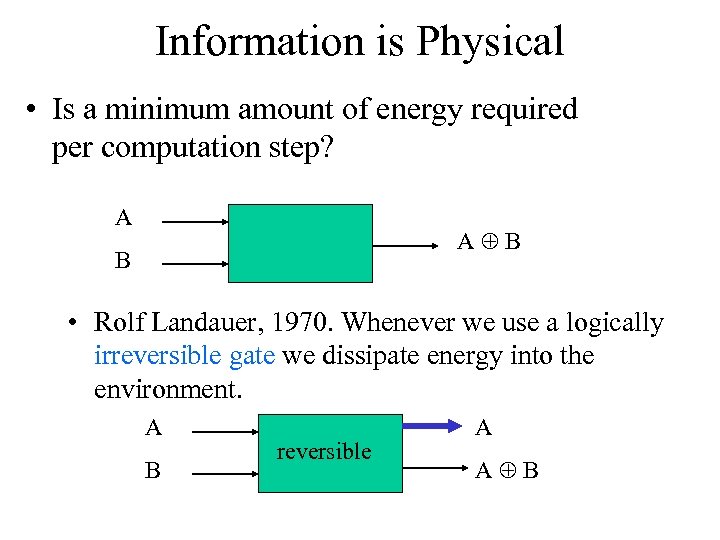
Information is Physical • Is a minimum amount of energy required per computation step? A A B B • Rolf Landauer, 1970. Whenever we use a logically irreversible gate we dissipate energy into the environment. A B reversible A A B

Information is Physical • Charles Bennett, 1973: There are no unavoidable energy consumption requirements per step in a computer. • Power dissipation of reversible circuit, under ideal physical circumstances, is zero. • Tomasso Toffoli, 1980: There exists a reversible gate which could play a role of a universal gate for reversible circuits. A B C Reversible and universal A B C AB

Reversible computation: • Landauer/Bennett: almost all operations required in computation could be performed in a reversible manner, thus dissipating no heat! • The first condition for any deterministic device to be reversible is that its input and output be uniquely retrievable from each other. – This is called logical reversibility. • The secondition: a device can actually run backwards then it is called physically reversible – and the second law of thermodynamics guarantees that it dissipates no heat. Billiard Ball Model

Reversible logic Reversible are circuits (gates) that have one-to -one mapping between vectors of inputs and outputs; thus the vector of input states can be always reconstructed from the vector of output states. INPUTS OUTPUTS 000 2 4 001 3 6 010 011 100 101 110 111 4 2 5 3 6 5 (2, 4)(365)

Reversible logic Reversible are circuits (gates) that have the same number of inputs and outputs and have one-toone mapping between vectors of inputs and outputs; thus the vector of input states can be always reconstructed from the vector of output states. INPUTS OUTPUTS 000 2 4 001 3 6 010 Feedback not allowed 011 4 2 100 Fan-out not allowed 101 6 5 110 111 5 3 (2, 4)(365)

Reversible logic constraints Feedback not allowed in combinational part In some papers allowed under certain conditions Fan-out not allowed In some papers allowed in a limited way in a “near reversible” circuit

• To understand reversible logic, it is useful to have intuitive feeling of various models of its realization.

Conservative Reversible Gates

Definitions • A gate with k inputs and k outputs is called a k*k gate. • A conservative circuit preserves the number of logic values in all combinations. • In balanced binary logic the circuit has half of minterms with value 1.

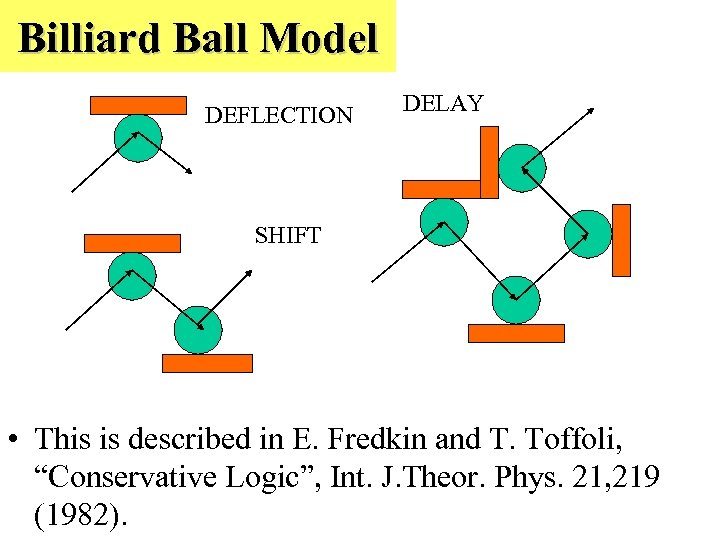
Billiard Ball Model DEFLECTION DELAY SHIFT • This is described in E. Fredkin and T. Toffoli, “Conservative Logic”, Int. J. Theor. Phys. 21, 219 (1982).

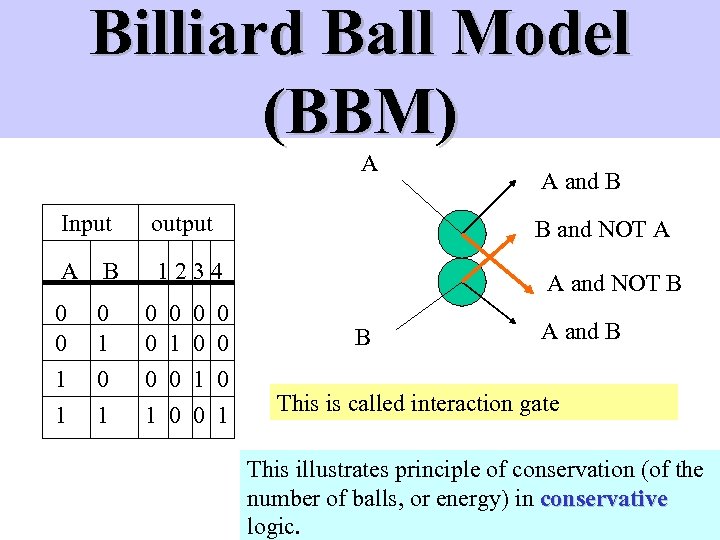
Billiard Ball Model (BBM) A Input output A B 1234 0 0 0 1 1 0 1 0 0 1 A and B B and NOT A A and NOT B B A and B This is called interaction gate This illustrates principle of conservation (of the number of balls, or energy) in conservative logic.

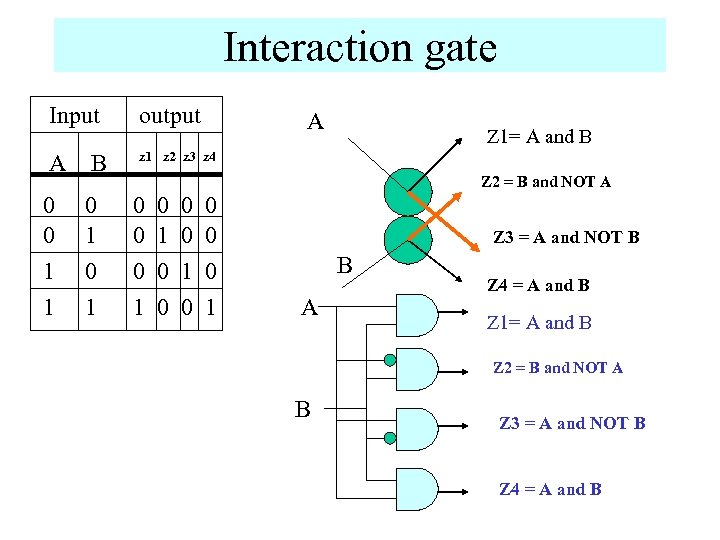
Interaction gate Input output A B z 1 z 2 z 3 z 4 0 0 1 1 0 1 A Z 1= A and B Z 2 = B and NOT A 0 0 0 1 0 0 0 0 1 Z 3 = A and NOT B B A Z 4 = A and B Z 1= A and B Z 2 = B and NOT A B Z 3 = A and NOT B Z 4 = A and B

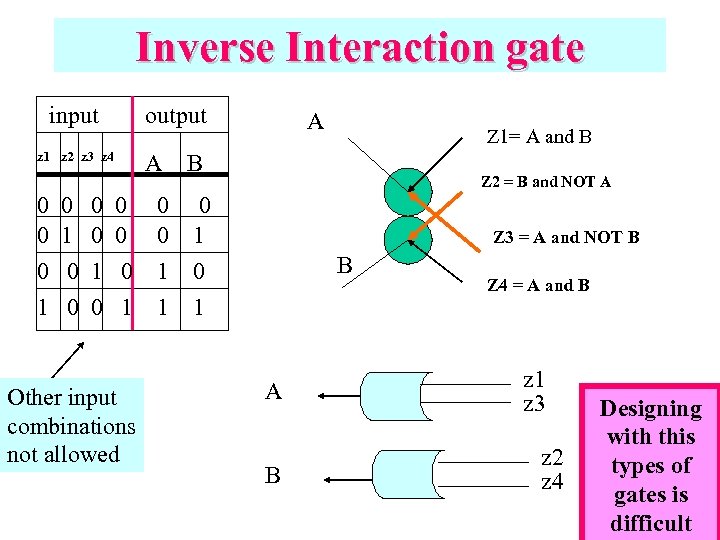
Inverse Interaction gate input output z 1 z 2 z 3 z 4 0 0 0 1 0 A 0 0 0 1 Other input combinations not allowed 0 0 1 1 A Z 1= A and B B Z 2 = B and NOT A 0 1 Z 3 = A and NOT B B A B Z 4 = A and B z 1 z 3 z 2 z 4 Designing with this types of gates is difficult

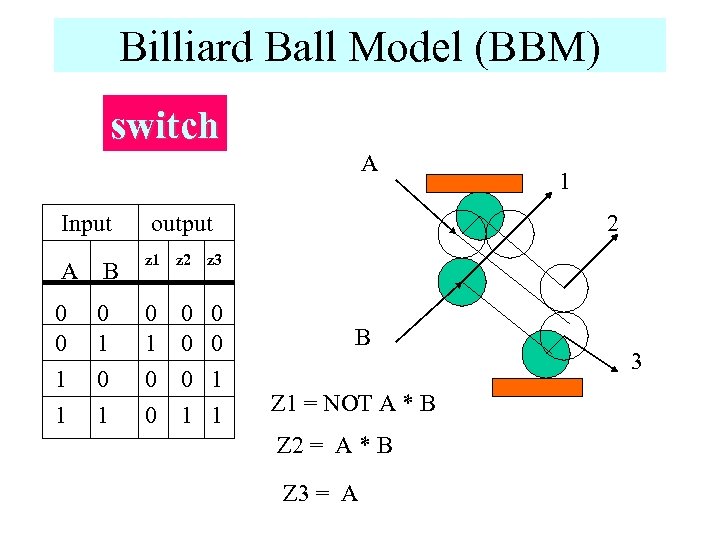
Billiard Ball Model (BBM) switch A Input A B 0 0 1 1 0 1 2 output z 1 z 2 z 3 0 1 0 0 1 1 1 B Z 1 = NOT A * B Z 2 = A * B Z 3 = A 3

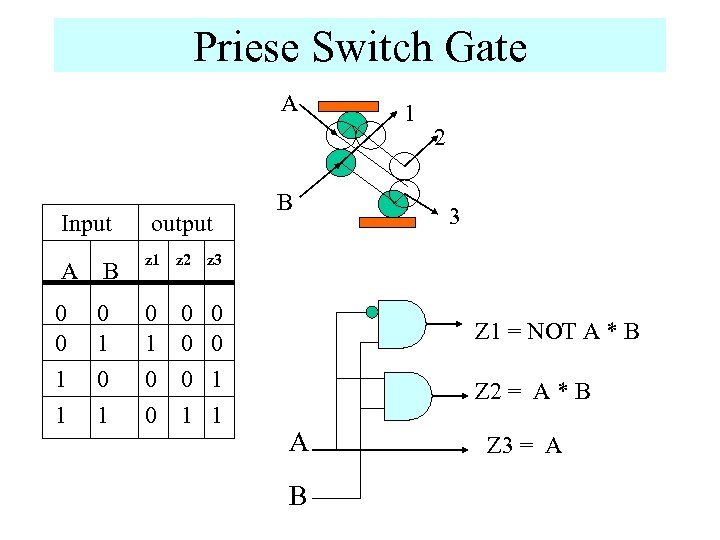
Priese Switch Gate A Input A B 0 0 1 1 0 1 output z 1 z 2 0 0 0 1 1 2 3 z 3 0 1 0 0 B 1 Z 1 = NOT A * B Z 2 = A * B A B Z 3 = A

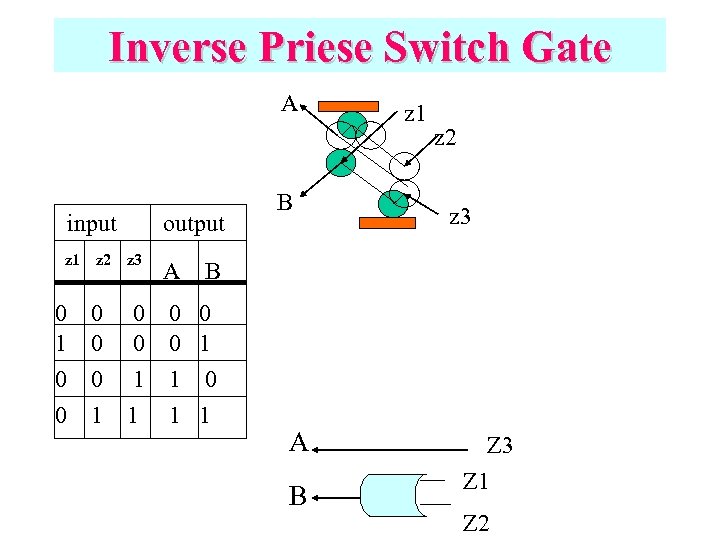
Inverse Priese Switch Gate A input z 1 z 2 output z 3 A B z 1 z 2 z 3 B 0 1 0 0 0 1 1 0 1 1 A B Z 3 Z 1 Z 2

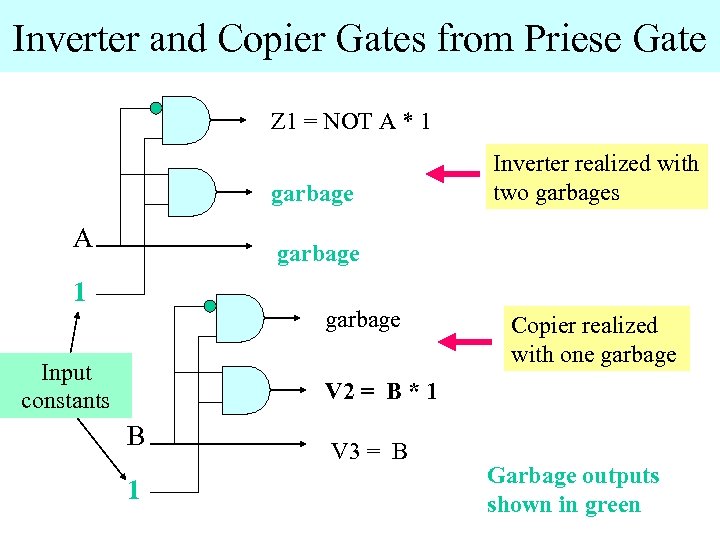
Inverter and Copier Gates from Priese Gate Z 1 = NOT A * 1 garbage A Inverter realized with two garbages garbage 1 garbage Input constants Copier realized with one garbage V 2 = B * 1 B 1 V 3 = B Garbage outputs shown in green

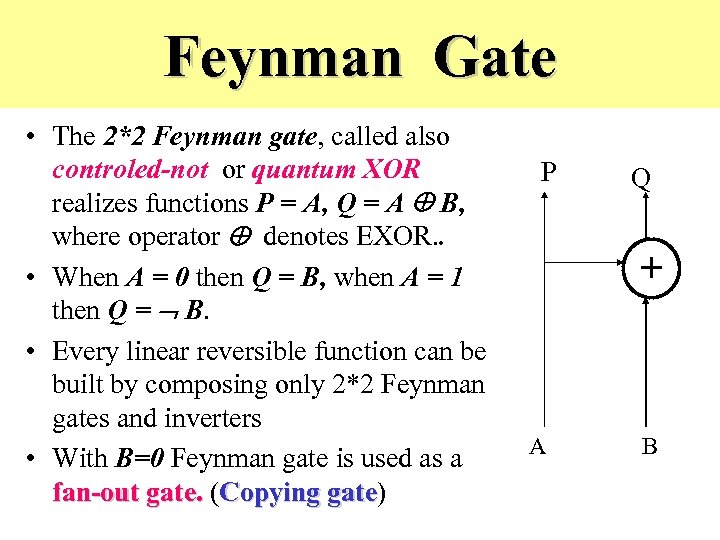
Feynman Gate • The 2*2 Feynman gate, called also controled-not or quantum XOR realizes functions P = A, Q = A B, where operator denotes EXOR. . • When A = 0 then Q = B, when A = 1 then Q = B. • Every linear reversible function can be built by composing only 2*2 Feynman gates and inverters • With B=0 Feynman gate is used as a fan-out gate. (Copying gate) gate P Q + A B

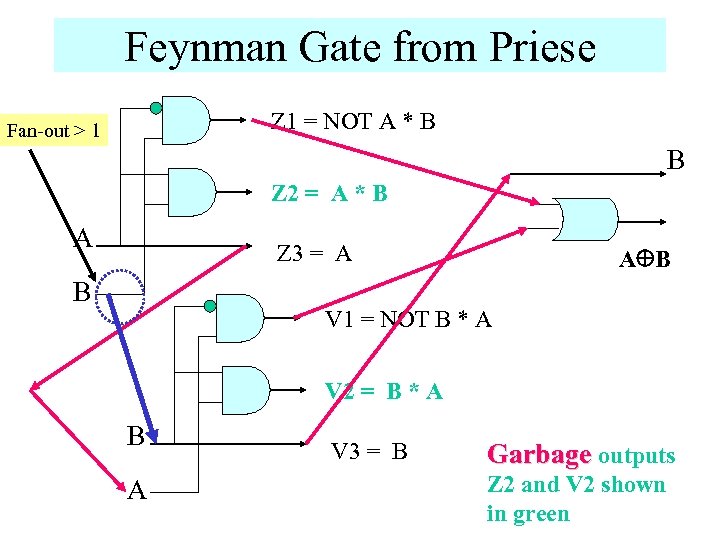
Feynman Gate from Priese Z 1 = NOT A * B Fan-out > 1 B Z 2 = A * B A Z 3 = A B V 1 = NOT B * A V 2 = B * A B A V 3 = B Garbage outputs Z 2 and V 2 shown in green

Fredkin Gate – Fredkin Gate is a fundamental concept in reversible and quantum computing – Every Boolean function can be build from 3 * 3 Fredkin gates: P = A, Q = if A then C else B, R = if A then B else C.

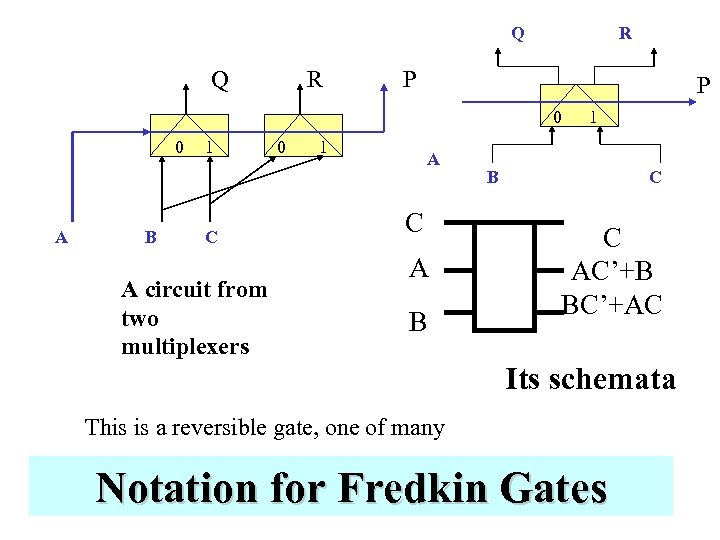
Q Q R R P P 0 0 A B 1 C A circuit from two multiplexers 0 1 A C A B 1 B C C AC’+B BC’+AC Its schemata This is a reversible gate, one of many Notation for Fredkin Gates

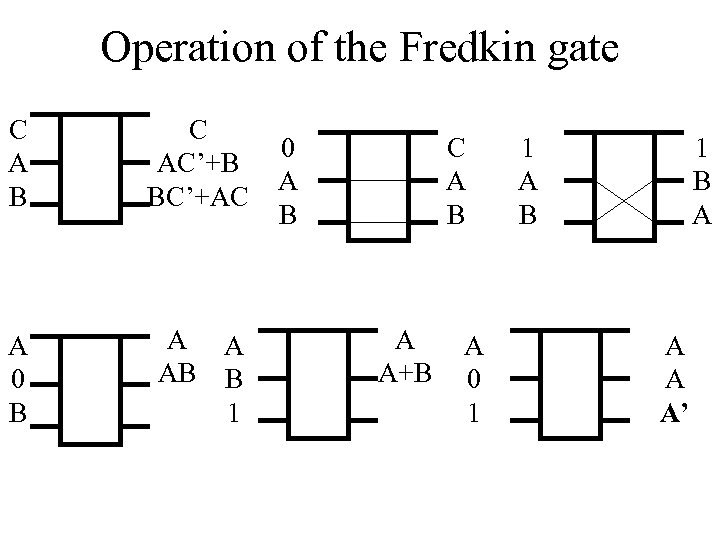
Operation of the Fredkin gate C A B C AC’+B BC’+AC A 0 B A A AB B 1 0 A B C A B A A+B A 0 1 1 A B 1 B A A’

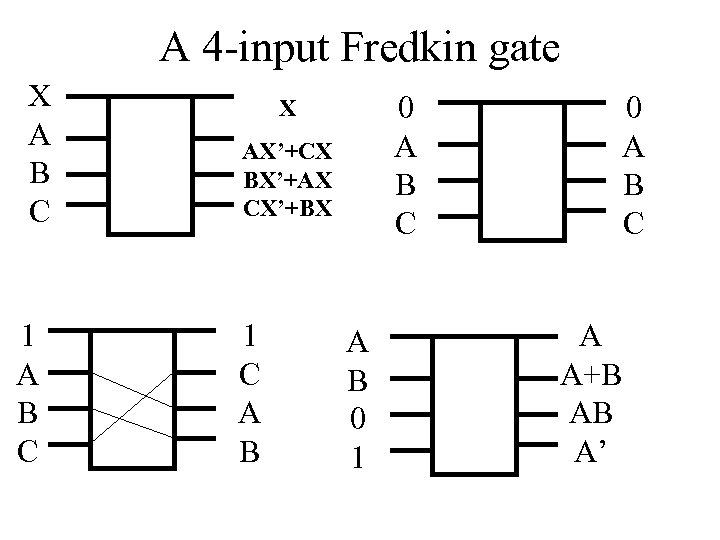
A 4 -input Fredkin gate X A B C 1 A B C 0 A B C X AX’+CX BX’+AX CX’+BX 1 C A B 0 1 0 A B C A A+B AB A’

Optical Conservative Reversible and Nearly Reversible Gates

Integrated optics • Integrated optics offers a particularly interesting candidate for implementing parallel, reversible computing structures • These structures operate in closer correspondence with the underlying microphysical laws which presume nondissipative interactions and global interconnections.

Reversible, Conservative, Optical Computers • Zero energy can be dissipated internally • Dissipation in such circuits would arise only in reading the output, which amounts for clearing the computer for further use. • Total decoupling of computational and thermal modes. • Decoupling is achieved by: – reversing the computation after the results have been computed, – restoring the circuit to its initial configuration

Requirements for gates • No distinction can be made between the inputs. • Each must be of the same type (in this case optical) and at the same level • The unrestricted type of gate permits a significant reduction in circuit’s complexity. • The circuit must be both optically reversible and information-theory (logic) reversible.

The device • An optical four-state nonlinear interface switching configuration is derived from the symmetry of an information-losless three-port structure • The device is: – bit-conservative – optically reversible – logically reversible – with dissipation related to the Kramers-Kronig inverse of the index of refraction

The device • The device inherently possesses three-terminal characteristics: – insensitivity to line-noise fluctuations (maintains high contrast between transmitted and reflected beams) – cascadability through bit conservation, – fan-out by pumped transparentization, – free-space optical fan-in, – pumped (total internal) reflected inversion. • Planar lattice-regularized layouts for binary adders

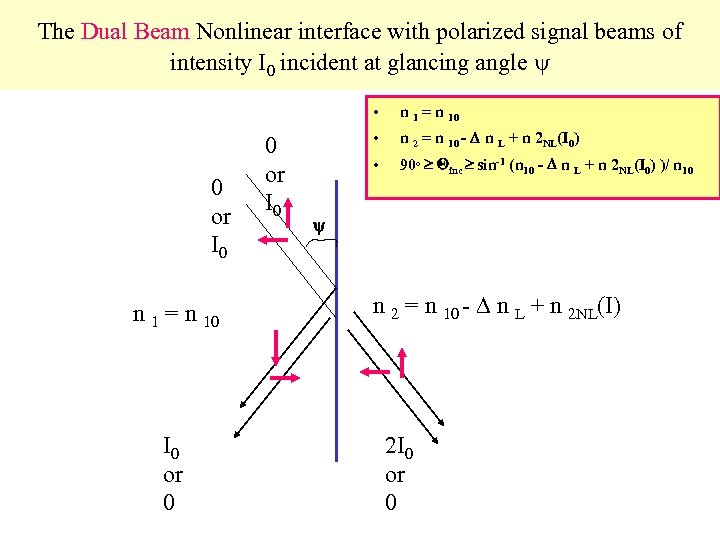
The Dual Beam Nonlinear interface with polarized signal beams of intensity I 0 incident at glancing angle • 0 or I 0 n 1 = n 10 I 0 or 0 0 or I 0 n 1 = n 10 • n 2 = n 10 - n L + n 2 NL(I 0) • 90 o inc sin-1 (n 10 - n L + n 2 NL(I 0) )/ n 10 n 2 = n 10 - n L + n 2 NL(I) 2 I 0 or 0

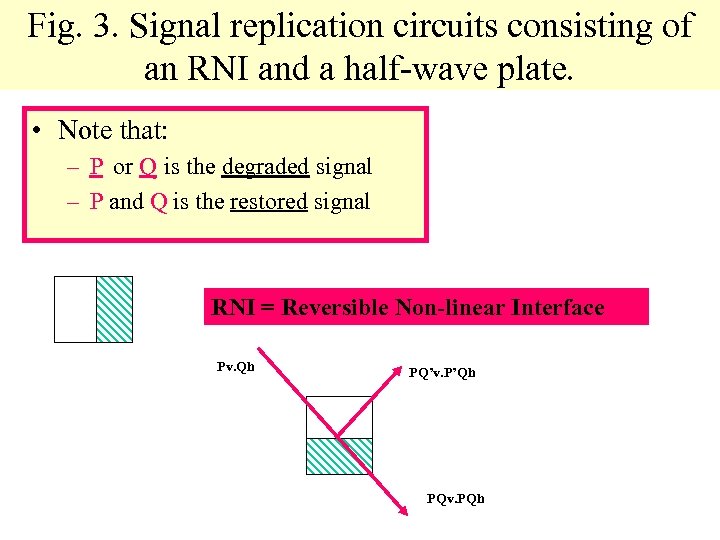
Fig. 3. Signal replication circuits consisting of an RNI and a half-wave plate. • Note that: – P or Q is the degraded signal – P and Q is the restored signal RNI = Reversible Non-linear Interface Pv. Qh PQ’v. P’Qh PQv. PQh

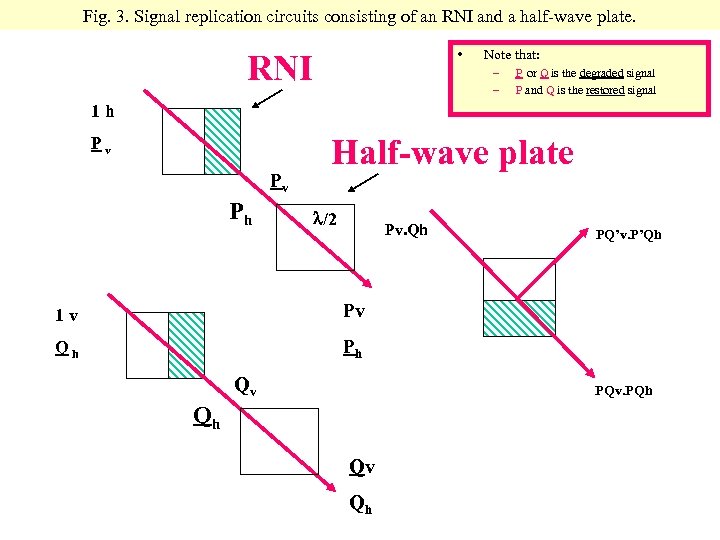
Fig. 3. Signal replication circuits consisting of an RNI and a half-wave plate. • RNI Note that: – – P or Q is the degraded signal P and Q is the restored signal 1 h Pv Pv Ph Half-wave plate /2 Pv. Qh 1 v Pv Qh PQ’v. P’Qh Ph Qv PQv. PQh Qh Qv Qh

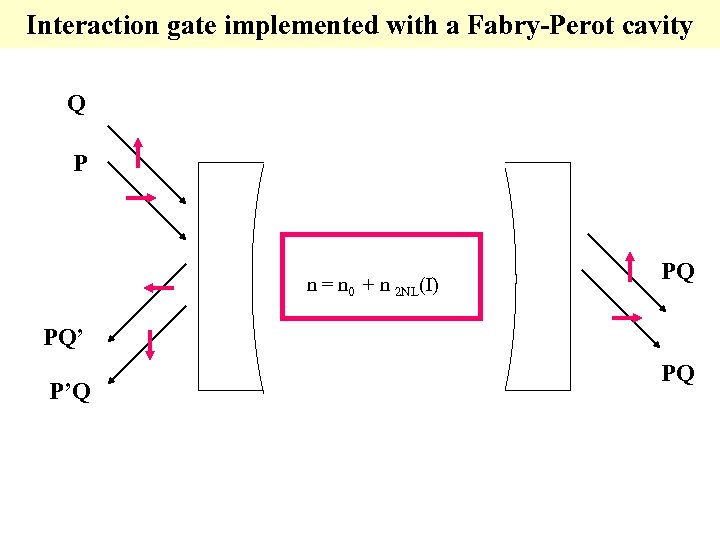
Interaction gate implemented with a Fabry-Perot cavity Q P n = n 0 + n 2 NL(I) PQ PQ’ P’Q PQ

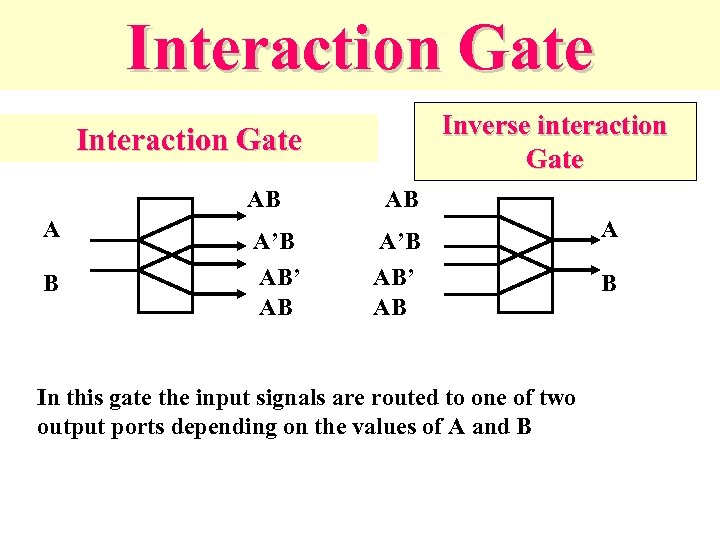
Interaction Gate Inverse interaction Gate Interaction Gate AB A B A’B AB’ AB AB A’B AB’ AB In this gate the input signals are routed to one of two output ports depending on the values of A and B A B

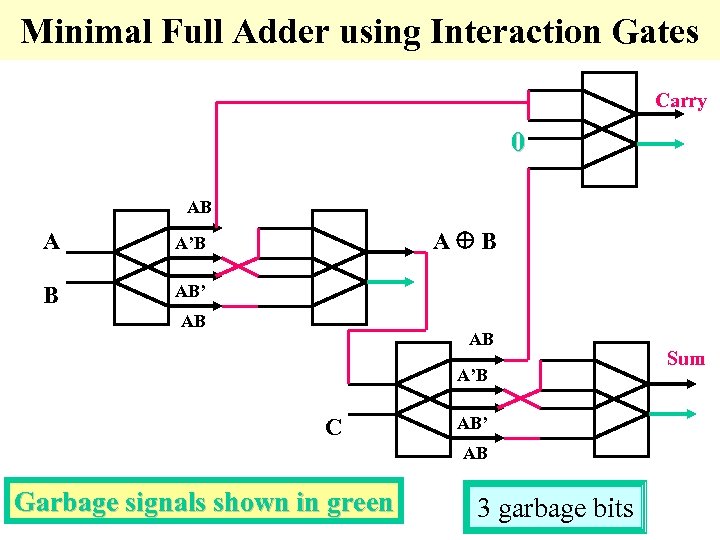
Minimal Full Adder using Interaction Gates Carry 0 AB A B A’B AB’ AB AB A’B C AB’ AB Garbage signals shown in green 3 garbage bits Sum

Reversible logic: Garbage • A k*k circuit without constants on inputs which includes only reversible gates realizes on all outputs only balanced functions, therefore it can realize non-balanced functions only with garbage outputs.

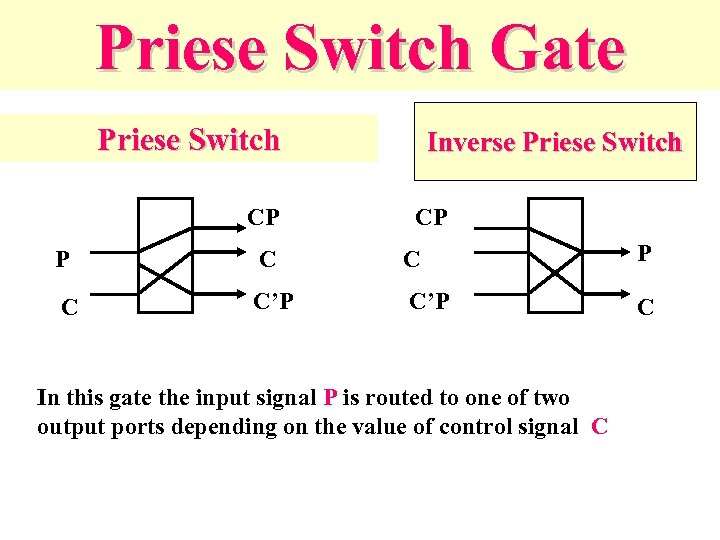
Priese Switch Gate Priese Switch CP Inverse Priese Switch CP P C C’P C In this gate the input signal P is routed to one of two output ports depending on the value of control signal C

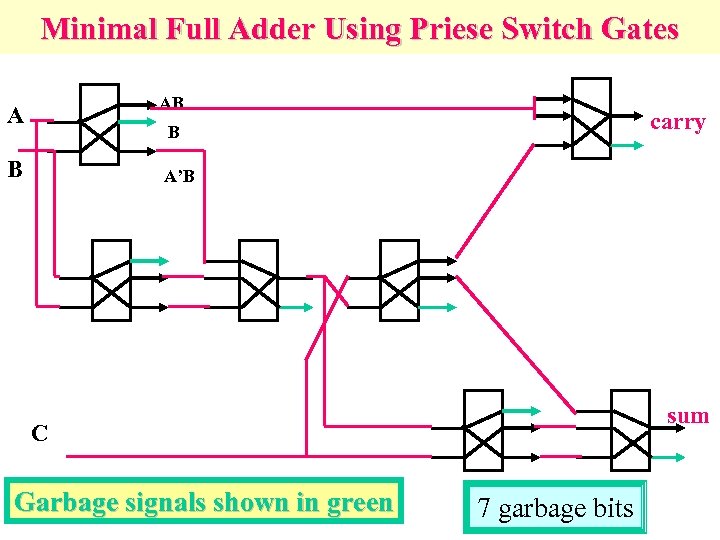
Minimal Full Adder Using Priese Switch Gates AB A carry B B A’B sum C Garbage signals shown in green 7 garbage bits

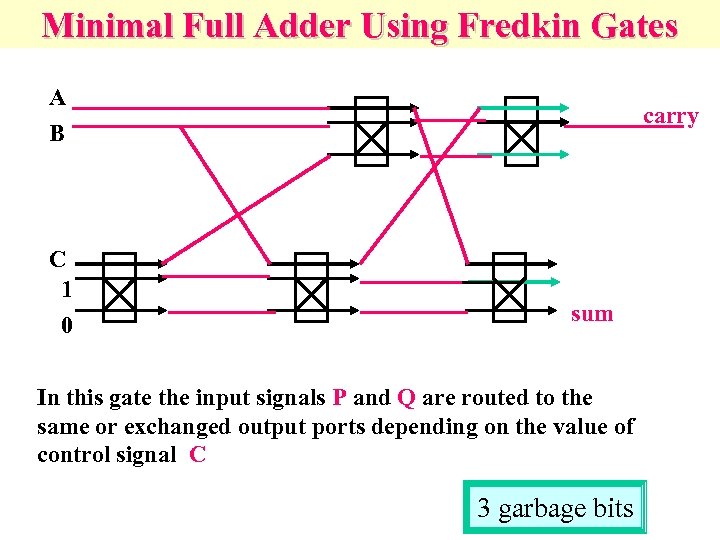
Minimal Full Adder Using Fredkin Gates A B C 1 0 carry sum In this gate the input signals P and Q are routed to the same or exchanged output ports depending on the value of control signal C 3 garbage bits

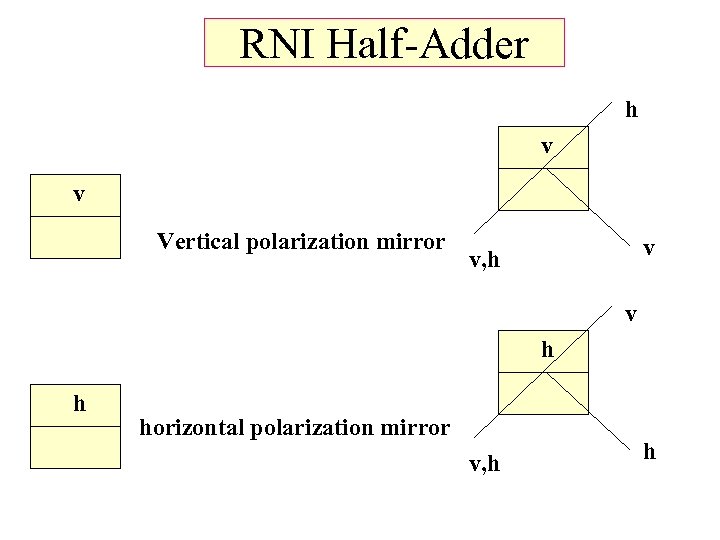
RNI Half-Adder h v v Vertical polarization mirror v v, h v h h horizontal polarization mirror v, h h

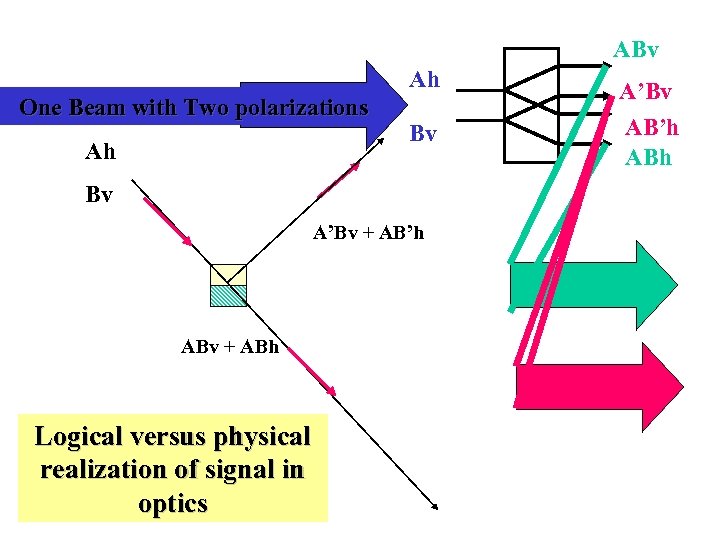
ABv Ah One Beam with Two polarizations Ah Bv Bv A’Bv + AB’h ABv + ABh Logical versus physical realization of signal in optics A’Bv AB’h ABh

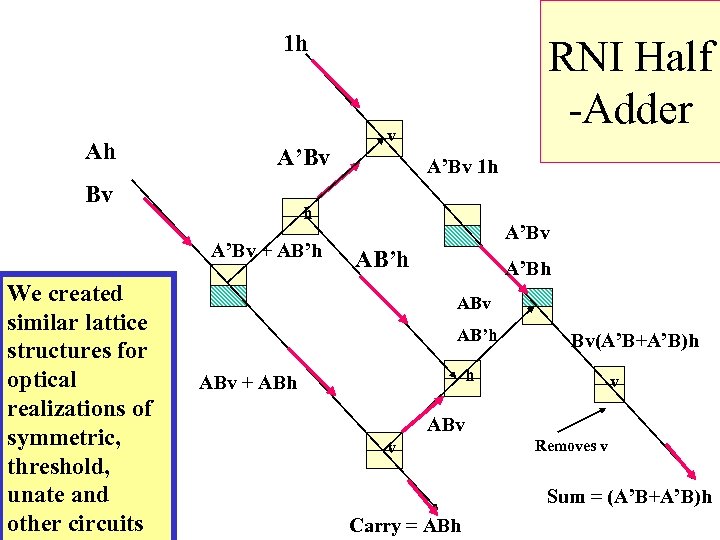
1 h Ah A’Bv Bv v A’Bv 1 h h A’Bv + AB’h We created similar lattice structures for optical realizations of symmetric, threshold, unate and other circuits RNI Half -Adder A’Bv AB’h A’Bh ABv AB’h Bv(A’B+A’B)h h ABv + ABh v ABv v Removes v Sum = (A’B+A’B)h Carry = ABh

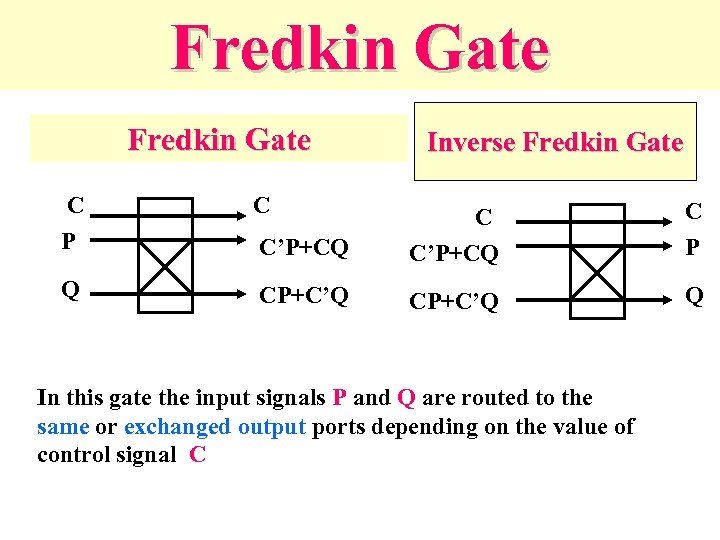
Fredkin Gate C P C Q Inverse Fredkin Gate C’P+CQ C P CP+C’Q Q In this gate the input signals P and Q are routed to the same or exchanged output ports depending on the value of control signal C

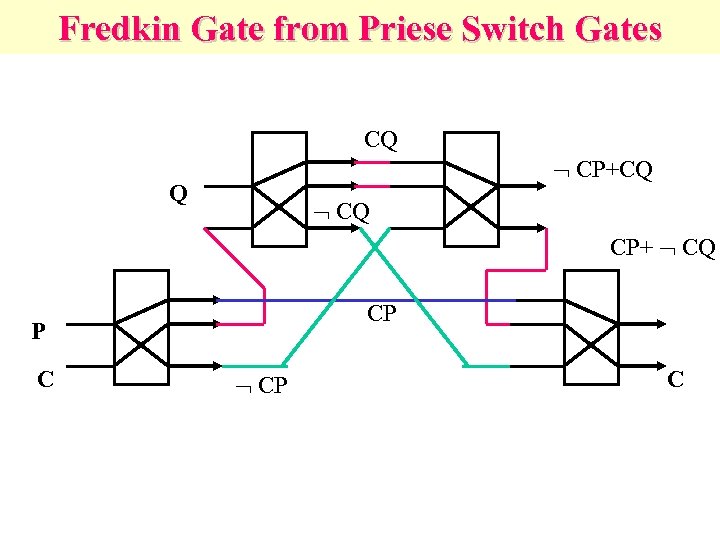
Fredkin Gate from Priese Switch Gates CQ CP+CQ Q CQ CP+ CQ CP P C CP C

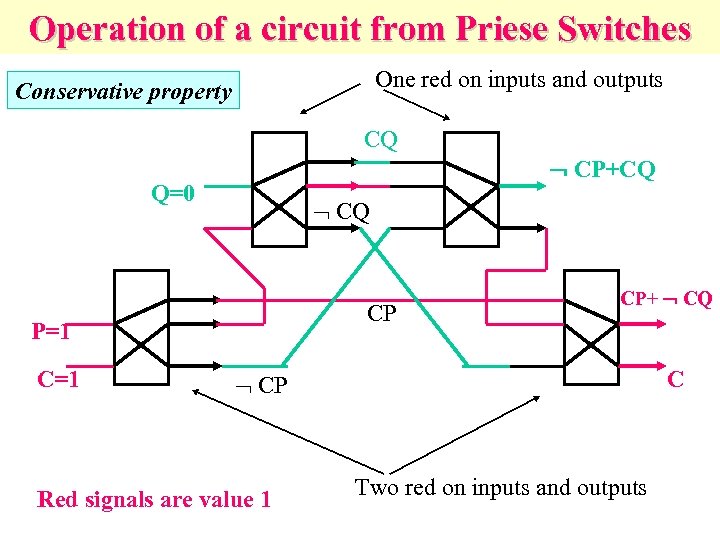
Operation of a circuit from Priese Switches One red on inputs and outputs Conservative property CQ CP+CQ Q=0 CQ CP P=1 CP+ CQ C CP Red signals are value 1 Two red on inputs and outputs

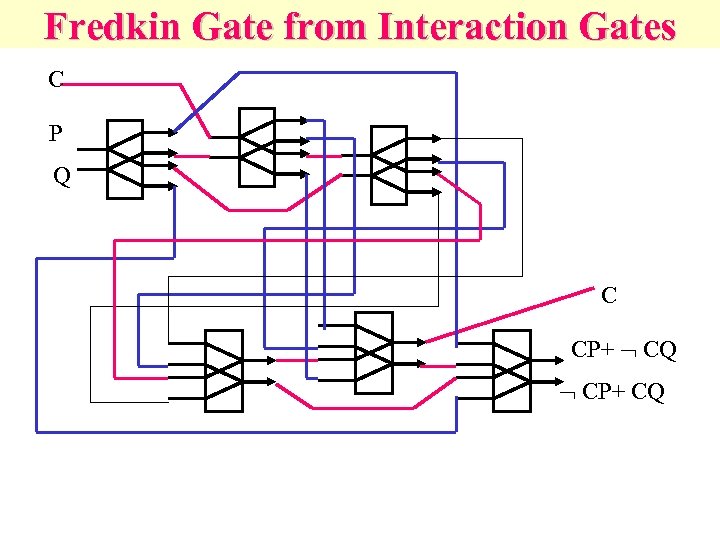
Fredkin Gate from Interaction Gates C P Q C CP+ CQ CP+ CQ

Concluding on the Billiard Ball Model • The interaction and Priebe gates are reversible and conservative, but have various numbers of inputs and outputs • Their inverse gates required to be given only some input combinations • From now on, we will assume the same number of inputs and outputs in gates. • INVERTER, FREDKIN and FEYNMAN gates can be created from Billiard Ball Model. • There is a close link of Billiard Ball Model and Optical gates and other physical models on micro level • Many ways to realize universal optical gates, completely or partially reversible but conservative

Quantum versus reversible computing • Quantum Computing is a coming revolution – after recent demonstrations of quantum computers, there is no doubt about this fact. They are reversible. • Top world universities, companies and government institutions are in a race. • Reversible computing is the step-by-step way of scaling current computer technologies and is the path to future computing technologies, which all happen to use reversible logic. – – – DNA biomolecular quantum dot NMR nano-switches • In addition, Reversible Computing will become mandatory because of the necessity to decrease power consumption

What to remember? 1. 2. 3. 4. 5. 6. 7. 8. 9. Importance of reversible logic Importance of conservative logic Billiard Ball model of computing. Gates of Billiard Ball model. Are they all reversible in traditional sense? – different type of reversibility? Priese or Switch gate. Interaction gate Realization of reversible gates in Billiard Ball model. Optical realization of reversible gates.