A Formal Descriptive Semantics of UML and Its

A Formal Descriptive Semantics of UML and Its Applications Hong Zhu Department of Computing and Electronics School of Technology

Acknowledgement v The work reported here is based on the outcomes of the collaborative research with Ø Dr. Ian Bayley, Oxford Brookes University, UK Ø Ms. Lijun Shan, National University of Defense Technology, China (visitor to Oxford Brookes University funded by China Scholarship Council) Ø Mr. Richard Amphlett, Oxford Brookes University, UK (Funded by Reinvention Centre as Undergraduate Research Student Scholarship)

Outline v What is descriptive semantics? Ø The concept and motivation v How to specify descriptive semantics? Ø The formal framework Ø Formal definition of mappings from diagrams to first order logic (FOPL) Ø Application to UML class, interaction and state machine diagrams Ø The relationships between descriptive semantics and functional semantics v Why descriptive semantics are important and useful? Ø Implementation of the semantics and the tool LANBDES Ø Applications in formal reasoning about models in FOPL

What is the meaning of UML diagrams? The system has two classes called Member and Book, 0. . 1 (There are two types of objects called Borrow members and books) 0. . 10 v There is an association between them, which is called Borrow Book (Members can borrow books) Library system v The upper limit of borrowing is 10 (Each member can only borrow up to 10 books at any time) Instances of the class Book v The upper limit for a book to be borrowed is 1 (Each book can only be borrowed by at Instances of the class Member most 1 member at any time) v

Semantics of modelling languages v ‘A model is a set of statement about some system under study’ [Seidwitz, 2003] Software model, and models in all scientific disciplines v The semantics of a modelling language is the satisfaction relationship |= between a model and A well-formed model a system. A system in the subject domain D, i. e. universe of systems that the language is modelling. s |= m in the modelling language. s is an instance of the model m, i. e. s satisfies the statements of the model m

Two types of semantics Descriptive semantics Functional semantics v Describe the system based on v Define how the system a set of basic concepts, such functions at run time. as class, association v Example: multiplicity upper bound, etc. Ø There are two types of objects called members and books. v Example: Ø Ø Ø The system has two classes called Member and Book Existing work on UML semantics often occurs as a combination of them. Example: Each instance of the Book class can only be borrowed by at most 1 member at any time.

Difficulties in the formalisation of UML v Interpretation in different subject domains: Ø One model can be interpreted in several different subject domains § Library system model: • When interpreted on the subject domain of real world systems, the library of Oxford Brookes University is an instance • When interpreted on the computer software, … v Extension with new concepts: Ø New basic concepts and constructs can be introduced through extension facilities, such as introduce new stereo types in profile definitions v Uses in different context: Ø One model may have different meanings in different context

Example: v Which of the following is the correct semantics of the model on the left? There are exactly three different classes such that …; Ø There at least three different classes such that …; Member Ø v Staff Student Which of the following programs can be considered as satisfied the model? class Member {…} class Staff extends Member {…} Class Student extends Member {…} class MSc. Student extends Student {…} class Member { public enum Member. Type { Staff, Student } public Member. Type. Of. Member; … } UML gives no definition on this issue!

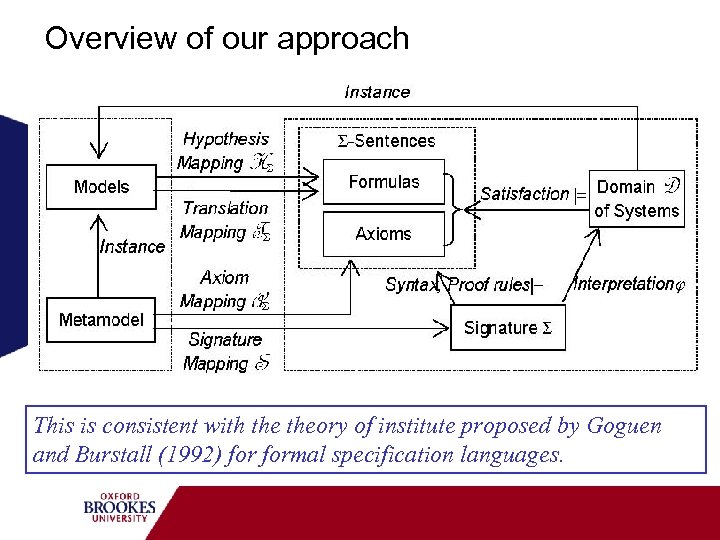Overview of our approach This is consistent with theory of institute proposed by Goguen and Burstall (1992) formal specification languages.

The formal framework Definition 1. (Semantics of a modelling language) A formal semantic definition of a modelling language consists of the following elements. l A signature Sig, which defines a formal logic system; l A set Axm. D of axioms about the descriptive semantics, which is in the formal logic system defined by Sig; l A set Axm. F of axioms about the functional semantics, which is also in the formal logic systems defined by Sig; l A mapping T from models to a set of formulas in the formal logic system defined by Sig. The formulas are the statements for the descriptive semantics of the model; l A mapping H from models to a set of formulas in the formal logic system defined by Sig. The formulas represent the hypothesis about the context in which the descriptive semantics is interpreted.

Definition 2. (Semantics of a model) Given a semantics definition of a modelling language as in Definition 1, the semantics of a model M under the hypothesis H, written Sem. H(M), is defined as follows. Sem. H(M) = Axm. D Axm. F T(M) H(M) where T(M) and H(M) are the sets of statements obtained by applying the semantic mappings T and H to model M, respectively. The descriptive semantics of a model M under the hypothesis H, written Des. Sem. H(M), is defined as follows. Des. Sem. H(M) = Axm. D T(M) H (M)

Satisfaction relation Definition 4. (Subject domain) A subject domain Dom of signature Sig with an interpretation Eva is a triple , where D is a collection of systems on which the formulas of the logic system defined by Sig can be evaluated according to a specific evaluation rule Eva. The value of a formula f evaluated according to the rule Eva in the context of system s D, written as Eva(f, s), is called the interpretation of the formula f in s. We write s|=Evaf, if a formula f is evaluated to true in a system s D, i. e. s|=Evaf iff Eva(f, s)= true. Definition 5. (Satisfaction of a model) Let Sig be a given signature and Dom a subject domain of Sig. A system s in D satisfies a model M according to a semantic definition Sem. H(M) if s|= Sem. H(M), i. e. for all formulas f in Sem. H(M), s|=f.

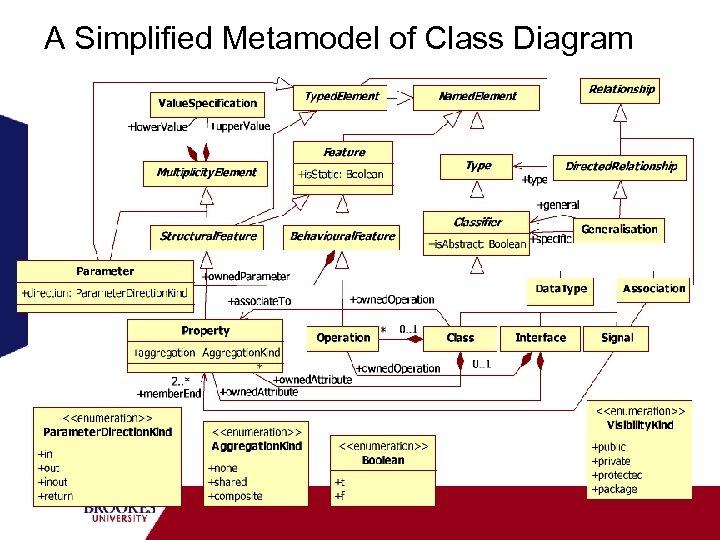A Simplified Metamodel of Class Diagram

Signature Mapping The signature mapping S from a metamodel M to a signature = S (M) is defined by a set of signature rules so that statements representing the descriptive semantics of models are sentences of first order predicates. Signature Rules S 1. For each metaclass named MC in the metamodel, we define a unary atomic predicate MC(x). S 2. For each metaassociation from a metaclass X to a metaclass Y in a metamodel, if MA is the association end on the Y side of the metaassociation, a binary predicates MA(x, y) is defined. S 3. For each metaattribute named MAttr of type MT in a metaclass MC in a metamodel, a unary function MAttr(x) is defined with domain MC and range MT. S 4. For each enumeration value EV given in an enumeration metaclass ME in a metamodel, a constant EV is defined.

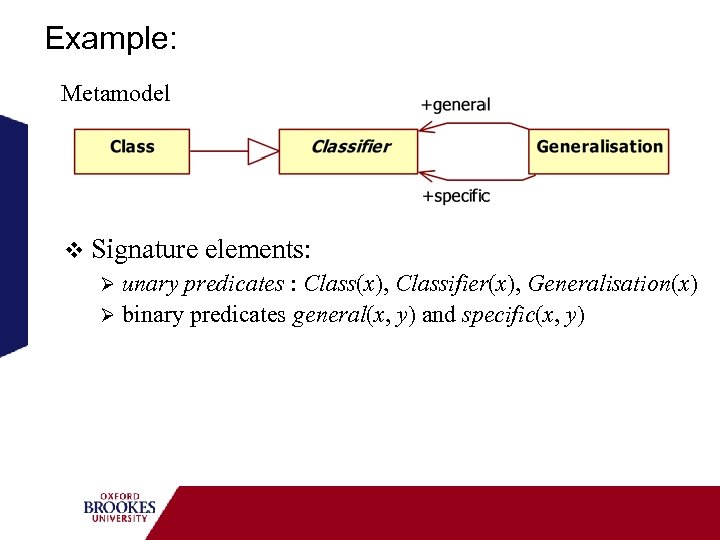Example: Metamodel v Signature elements: Ø unary predicates : Class(x), Classifier(x), Generalisation(x) Ø binary predicates general(x, y) and specific(x, y)

Translation mapping is defined by a set of translation rules that generate formulas in the signature from a UML model M. Translation Rules T 1: Classification of elements. For each identifier id of concrete type MC, a formula in the form of MC(id) is generated. T 2: Properties of elements. For each element a in the model and every applicable function MAttr that represents a metaattribute MAttr, a formula in the form of MAttr(a)=v is generated, where v is a’s value on the property. T 3: Relationships between elements. For each pair (e 1, e 2) of elements related by relationship R, a formula in the form of R(e 1, e 2) is generated to specify the relationship by applying binary predicate R(x 1, x 2).

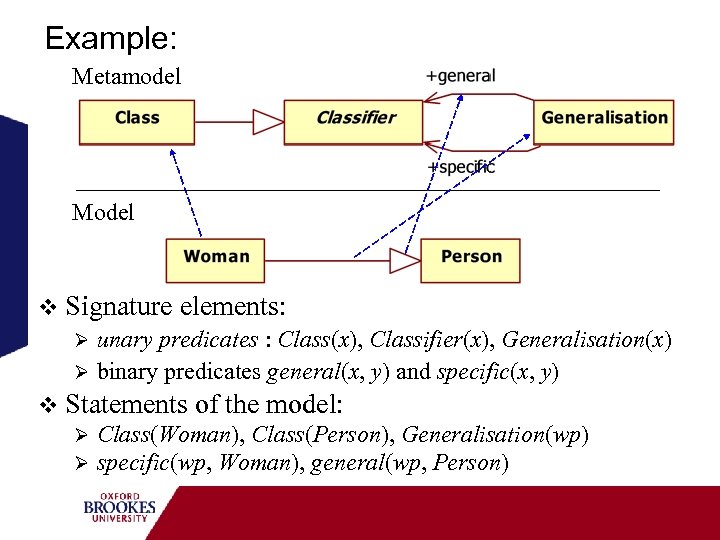Example: Metamodel Model v Signature elements: Ø unary predicates : Class(x), Classifier(x), Generalisation(x) Ø binary predicates general(x, y) and specific(x, y) v Statements of the model: Ø Class(Woman), Class(Person), Generalisation(wp) Ø specific(wp, Woman), general(wp, Person)

Interpretation in different contexts The context in which a model is interpreted can be specified as hypothesis. v A hypothesis can be defined as a rule that maps from a model to formulas in the signature. v Hypothesis Rules H 1: Distinguishability of elements. A hypothesis that the elements of type MC in the model are all different from each other can be generated as formulas in the form of ei ej, for i j {1, 2, …, k}. H 2: Completeness of elements. A hypothesis on the completeness of elements of type MC can be generated as a formula in the following form. x. MC(x) -> (x = e 1) (x = e 2) … (x = ek) H 3: Completeness of relations. A hypothesis on the completeness of relation R in the model can be generated as a formula in the following form. x 1, x 2. R(x 1, x 2)->((x 1=e 1, 1) (x 2=e 1, 2)) ((x 1= e 2, 1) (x 2= e 2, 2)) … ((x 1= en, 1) (x 2= en, 2))

Definition of functional semantics v Functional semantics defines the basic concepts of object orientation v Our approach: axioms in second order predicate logic Predicates at model level in descriptive semantics. v For example, Ø If class A inherits class B, every instance of A is also an instance of B Class(A) Class(B) Inherits(A, B) x (A(x) B(x)) A(x): object x is an instance of class A. It is a predicate at object level.

Object and class Axiom 1: Every object must be an instance of a class. x (Object(x) C. (Class(C) C(x))) This formula is now second order because C is a qualified variable range over predicates. Notation: Every class C in the system is represented as a predicate C(x) such that C(a) is true if and only if a is an instance of class C. Axiom 2: Every attribute declared in a class is a property of the class. Owned. Attribute(C, x) Has. Attribute(C, x) Axiom 3: Every operation declared in a class is an operation of the class Owned. Operation(C, x) Has. Operation(C, x)

Inheritance Axiom 4: If class A inherits class B, every instance of A is also an instance of B. Class(A) Class(B) Inherits(A, B) x (A(x) B(x)) Axiom 5: If class A inherits class B, every attribute of B is also an attribute of A Class(A) Class(B) Inherits(A, B) x (Property(x) Has. Attribute(B, x) Has. Attribute(A, x)) Axiom 6: If class A inherits class B, every operation of B is also an operation of A Class(A) Class(B) Inherits(A, B) x (Operation(x) Has. Operation(B, x) Has. Operation(A, x)) Inherits(A, B) = x (Generalisation(x) specific(x, A) general(x, B)

Re-definition and Polymorphism Let class A inherits class B. Axiom 7: If A declares attribute a with type TA, then the type of attribute a is TA regardless what is defined in class B. Class(A), Class(B), Inherits(A, B), Has. Attribute(A, a), Owned. Attribute(A, a), Type(a, TA) Current. Type(a, A, TA) Axiom 8: If class A does not declare attribute a, but inherited attribute from B, then the type of attribute a is as in B. Class(A), Class(B), Inherits(A, B), Has. Attribute(A, a), Owned. Attribute(A, a) ( Current. Type(a, B, TB) Current. Type(a, A, TB) Notation: Current. Type(a, A, B) means the current type of attribute a in class A is B. Note: There are similar axioms for operations.

Abstract class v Axiom 9: If class A is abstract, for every instance x of A, there must be a subclass B of A such that x is an instance of B. Class(A) Is. Abstract(A) x. (A(x) B. (Class(B) Inherits(B, A) B(x))) Notation: Is. Abstract(C) == Is. Abstract(C, True)

Attribute and association Axiom 10: Class(A) Has. Attribute(A, a) Current. Type(a, A, B) ( x, y. a(x, y) A(x) B(y)) A a: B Axiom 11: Class(A) Class(B) Association(a) member. End(a, Ea) Current. Type(Ea, A) member. End(a, Eb) Current. Type(Eb, B) ( x, y. Eb(x, y) A(x) B(y)) Ea A ( x, y. Ea(x, y) B(x) A(y)) a Eb B Notation: For any attribute or association a, a(x, y) denotes x. a=y. This is to keep notation consistent with the notation, e. g. Association(A, B) used in descriptive semantics derived from metamodel.

Multiplicity Axiom 12: Multiplicity of association Association(a) member. End(a, Ea) type(Ea, A) member. End(a, Eb) type(Eb, B) upper. Value(Eb, m) lower. Value(Eb, n) ( x. A(x) n ||{y | Eb(x, y) }|| m) Axiom 13: Multiplicity of attributes Class(A) owned. Attribute(A, a) type(a, B) upper. Value(a, m) lower. Value(a, n) ( x. A(x) n ||{y | a(x, y) }|| m)

Enumeration Axiom 14: Distinguishability of the literal constants Enumeration(A) owned. Literal(A, v 1) owned. Literal(A, v 2) (Identifier(v 1) Identifier(v 2 ) (v 1 v 2)) Axiom 15: Type of the literal constants Enumeration(A) owned. Literal(A, v) A(v) Axiom 16: Completeness of the enumeration Enum. Class(A) ( x. ( A(x) owned. Literal(A, x)))

Whole-part relationships Axiom 17: Composite relation (Class(A) Class(B) Association(C) member. End(C, b) type(b, B) aggregation(b, composite) ) x. (B(x) !y. (A(y) b(x, y))

Combination of functional and descriptive semantics v Applying functional semantics to models Ø ‘Ordinary’ semantics in first order logic, i. e. the properties that objects of the system at run time must satisfy For example, [Berardi, Cal and Calvanese, 2005], [Kaneiwa and Satoh, 2006], etc. v Applying functional semantics to metamodel Ø Axioms of models, i. e. the properties satisfied by all models

Apply functional semantics to model: Example Descriptive semantics Class(Woman), Class(Person), Generalisation(wp), specific(wp, Woman), general(wp, Person) , A, B (Class(A) Class(B) Inherits(A, B) x (A(x) B(x))) |- x (Woman(x) Person(x)) where Object level semantics Functional semantics Inherits(A, B) = x (Generalisation(x) specific(x, A) general(x, B)

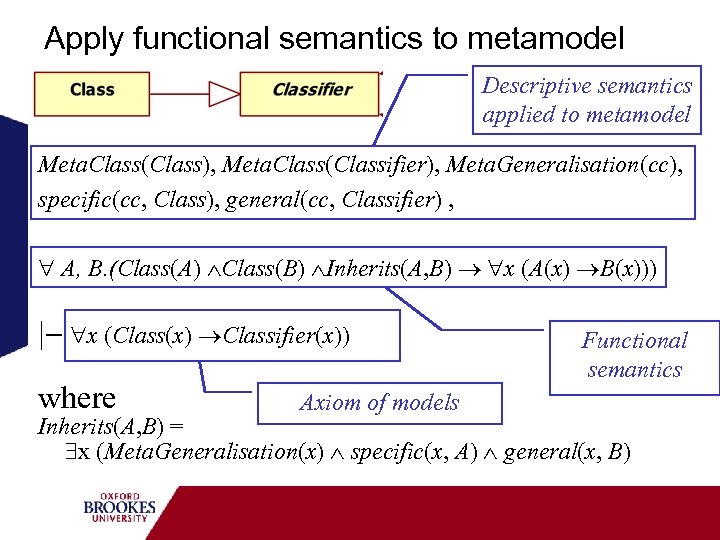Apply functional semantics to metamodel Descriptive semantics applied to metamodel Meta. Class(Class), Meta. Class(Classifier), Meta. Generalisation(cc), specific(cc, Class), general(cc, Classifier) , A, B. (Class(A) Class(B) Inherits(A, B) x (A(x) B(x))) |- x (Class(x) Classifier(x)) where Axiom of models Functional semantics Inherits(A, B) = x (Meta. Generalisation(x) specific(x, A) general(x, B)

Implementation of functional semantics The functional semantics for the OO concepts used in UML class diagram are defined as a set of rules that maps from class diagram (metamodel) to axioms (formulas of the -sentences) and implemented directly. Axiom rules: A 1: Completeness of classification. Let MC 1, MC 2, …, MCn be the set of concrete metaclasses in a metamodel. We have an axiom x. MC 1(x) MC 2(x) … MCn(x) A 2: Disjointness of classification. Let MC 1, MC 2, …, MCn be the set of concrete metaclasses in a metamodel. For each pair of different concrete metaclasses MCi and MCj, i j, we have an axiom x. MCi(x) ¬ MCj(x). A 3: Logical implication of inheritance. For a generalisation relation from metaclass MA to MB in a metamodel, we have an axiom x. MA(x) MB(x). Corresponding to Axiom 4 of functional semantics

Axiom Rules (Continue) A 4: Completeness of specialisations. Let MA be a metaclass in a metamodel and MB 1, MB 2, …, MBk be the set of metaclasses specialising MA. We have an axiom x. MA(x) MB 1(x) MB 2(x) … MBk(x). A 5: Types of parameters of predicates. Corresponding to Axiom 10 For each binary predicate MA(x, y) derived from an association from metaclass MC 1 to MC 2 in a metamodel, we have an axiom x, y. MA(x, y) MC 1(x) MC 2(y). A 6: Domain and range of functions. Corresponding to Axiom 11 For each function MAttr(x) derived from a metaattribute MAttr of type MT in a metaclass MC, we have an axiom x, y. MC(x) (MAttr(x) = y) MT(y). A 7: Multiplicity of binary predicate. For each binary predicate MA(x, y) derived from an association from metaclass MC 1 to MC 2 in a metamodel, let Mul be the multicity value specified on the association end MA, we have axioms in the following form. If Mul = 0. . 1: x, y, z. MC 1(x) MA(x, y) MA(x, z) (y = z) If Mul = 1 or unspecified: x. MC 1(x) y. MA(x, y) and Corresponding x, y, z. MC 1(x) MA(x, y) MA(x, z) (y = z) to Axiom 12 If Mul = 1. . *: x. MC 1(x) y. MA(x, y) If Mul = 2. . *: x. MC 1(x) y, z. MA(x, y) MA(x, z) (y z) If Mul = 0. . 2: x, y, z, u. MC 1(x) MA(x, y) MA(x, z) MA(x, u) (y = z) (y = u) (u = z)

Axiom Rules (continue) Corresponding to Axiom 13 A 8: Multiplicity of function. For each function MAttr(x) derived from a metaattribute MAttr of type MT in a metaclass MC, let Mul be the multicity value of the metaattribute MAttr, we have axioms: If Mul = 0. . 1: x, y, z. MC(x) (MAttr(x) = y) (MAttr(x) = z) -> (y = z) If Mul = 1: x. MC(x) -> y. (MAttr(x) = y) and x, y, z. MC(x) (MAttr(x) = y) (MAttr(x) = z) -> (y = z) Corresponding to If Mul = 1. . *: x. MC(x) -> y. (MAttr(x) = y) Axiom 14 A 9: Distinguishability of the literal constants. For each pair of different literal values a and b of an enumeration type, we have an axiom a b. Corresponding to Axiom 15 A 10: Type of the literal constants. For each enumeration value a defined in an enumeration metaclass ME, we have an axiom in the form of ME(a) stating that the type of a is ME. A 11: Completeness of the enumeration. An enumeration type only contains the listed literal constants as its values, hence for each enumeration metaclass ME with literal values a 1, a 2, …, ak, we have an axiom in the form of Corresponding to Axiom 16 x. ME(x) -> (x = a 1) (x = a 2) … (x = ak). Axiom Rule 12: Well-formedness rules. For each WFR formally specified in OCL, we have a corresponding axiom in the first order language.

Strict metamodelling principle v Axiom rules also contain ‘hypothesis’ on the uses of class diagrams as metamodels, such as the strict meta-modelling principle, which is to ensure that a metamodel is a well-defined abstract syntax of modelling language. Strict Metamodelling: In an n-level modelling architecture M 0, M 1, …, Mn, every element of an Mm-level model must be an instance-of exactly one element of an Mm+1 -level model, for all 0 m < n-1, and any relationship other than the instance-of relationship between two elements X and Y implies that level(X ) = level(Y). Corresponding to axiom rules A 1, A 2 and A 4.

Semantics of Interaction and State Machine Same signature, axiom and formula mappings are applied to the meta-models of UML state machine and interaction diagrams. v Additional Axiom Rules for inter-metamodel connections v Axiom Rules A 10: Cross metamodel association and inheritance. For each cross metamodel inheritance from metaclass MA to external metaclass MB, we have an axiom in the form of x. MA(x) -> MB(x). A 2’: Completeness of specialisations across metamodels. Let MA be a metaclass depicted in two metamodels MM 1 and MM 2. Let metaclasses MB 1, MB 2, …, MBk be the set of metaclasses that specialise MA in metamodel MM 1, and MC 1, MC 2, …, MCp be the set of metaclasses that specialise MA in metamodel MM 2. We have the following axiom when a model is defined by MM 1 and MM 2. x. MA(x) -> MB 1(x) … MBk(x) MC 1(x) … MCp(x)

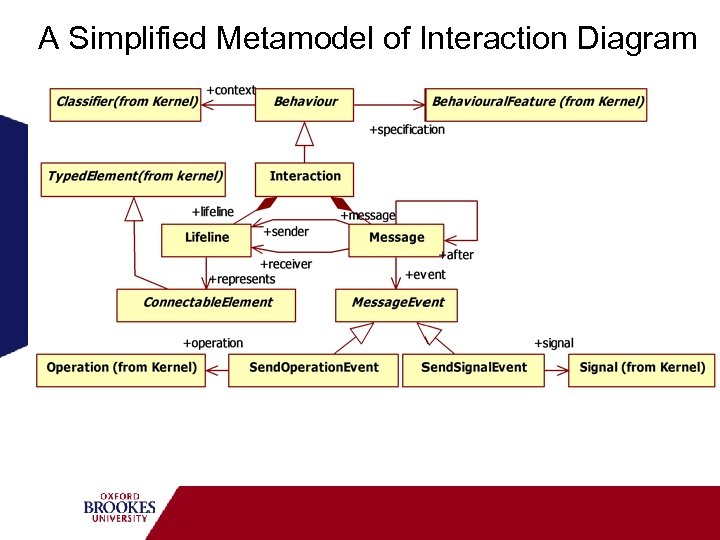A Simplified Metamodel of Interaction Diagram

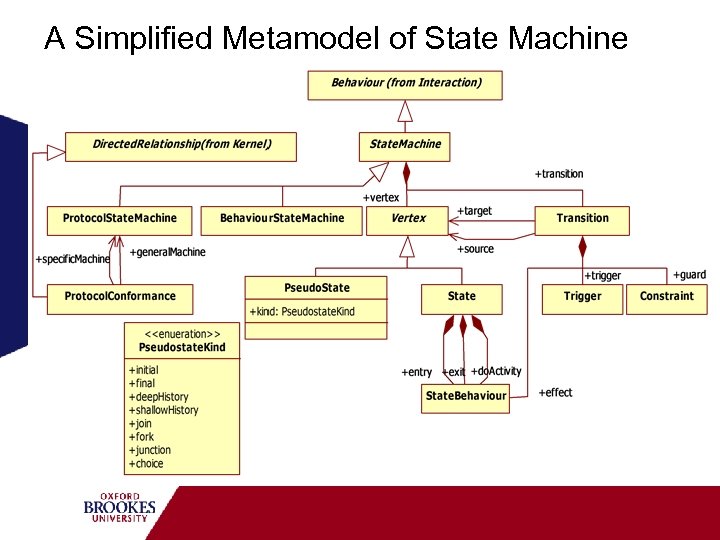A Simplified Metamodel of State Machine

The Tool LAMBDES stands for Logic Analyser of Model/Metamodel Based on Descriptive Semantics

Applications of Descriptive Semantics Definition 3. (Properties of a model) Let Sem. H(M) be the semantics of a model M. M has a property P (represented as a formula in the logic system defined by Sig) under the semantics definition Sem. H(M) and the hypothesis H, if and only if Axm. D Axm. F T(M) H(M) |- P in the formal logic system. Similarly, we say that M has a property P in descriptive semantics, if and only if Axm. D T(M) H(M) |- P in the formal logic system. v v v Consistency checking of UML models Validation of consistency constraints for UML models Consistency checking of UML meta-models Conformance checking of designs to design patterns Consistency checking of specification of design patterns

Consistency checking of UML models Definition 6. (Logical consistency) Let Sem. H(M) = Axm. D Axm. F T(M) H(M) be the semantics of a model M. Model M is said to be logically inconsistent in the semantic definition Sem. H(M) if Sem. H(M)|-false; otherwise, we say that the model is logically consistent. Definition 7. (Consistent interpretation of formulas in a subject domain) Let Dom= be a subject domain as defined in Definition 4. The interpretation of formulas in signature Sig is consistent with first order logic if and only if for all formulas q and p 1, p 2, …, pk that p 1, p 2, …, pk |- q, and for all systems s in D that Eva(pi, s) =true for i=1, 2, …, k, we always have Eva(q, s) =true.

Validity of consistency checking Theorem 1. (Unsatisfiability of inconsistent model) A model M that is logically inconsistent in the semantic definition Sem. H(M) is not satisfiable on any subject domain whose interpretation of formulas is consistent with first order logic. Ø Ø Ø Inconsistent model => it cannot be implemented (not satisfiable) Consistency model => not necessarily implementable Other issues effect satisfiability: l Property of the subject domain: e. g. whether the programming language is powerful enough to implement l Non-logic property of the model: e. g. whether the system is feasible

Validation of consistency constraints v Consistency constraints: Ø Logic statements about models, Ø e. g. ‘a life line must represent an instance of a class’ x, y, z. Lifeline(x) represent(x, y) type(y, z) -> Class(z) Definition 8. (Consistency w. r. t. consistency constraints) Given a set of consistency constraints C={c 1, c 2, …, cn}, the consistency of a model M with respect to the constraints C under the semantics definition Sem. H(M) is the consistency of the set U = Sem. H(M) C of formulas. In particular, we say that a model fails on a specific constraint ck, if Sem. H(M) is consistent, but Sem. H(M) {ck} is not. Results of experiments: • A number of sample UML models were checked to be consistent. • Mutants of the models were checked and detected inconsistency in mutants.

Definition of validity and effectiveness Definition 9. (Validity of consistency constraints) Let Axm. D and Axm. F be the sets of axioms for descriptive semantics and functional semantics, respectively. A set C={c 1, c 2, …, cn} of consistency constraints is descriptively valid if Axm. D C is logically consistent. The set C of consistency constraints is functionally valid Axm. D Axm. F C is logically consistent. Definition 10. (Effectiveness of consistency constraints) Let A be a set of semantics axioms. A set C={c 1, c 2, …, cn} of consistency constraints is logically ineffective with respect to the set A of axioms if A |- C. Results of Experiments: A set of 5 consistency constraints were validated by using LAMBDES tool. They were proved valid and effective.

Consistency checking of meta-models Definition 11 (Inconsistency of meta-model). A meta-model M is inconsistent if Axm. D(M) is logically inconsistent. Experiments: Ø Subjects: Simplified UML, UML 2. 0 metamodel, Aspect. J profile Ø Findings: Ø Simplified metamodel: consistent Ø UML 2. 0: Ø 16 inconsistencies due to voilation of strict meta-modelling Ø 1 inconsistently as abstract and concrete metaclasses in different metamodel class diagrams. Ø Aspect. J: ØIncomplete definition of 7 meta-classes Ø 2 inconsistency due to violation of strict meta-modelling

Conformance of designs to patterns v Patterns are meta-models (rather than models) Ø A pattern specifies a set of models that have common structural and behavioural properties Ø A pattern can be specified as a predicate on models in first order logic (Bayley and Zhu 2007, 2008)

Translation of pattern specification v A specification of design pattern is translated into a specification of systems in sig-formulas Template Method Specification formula(exists([ %Components: x. Abstract. Class, x. Template. Method, x. Others ], and( %Static conditions: Class(x. Abstract. Class), owned. Operation(x. Abstract. Class, x. Template. Method), owned. Operation(x. Abstract. Class, x. Others), is. Leaf(x. Template. Method, b. True), not(equal(x. Template. Method, x. Others)), is. Leaf(x. Others, b. False) %Dynamic conditions: calls. Hook(x. Template. Method, x. Others) ))).

Validity of conformance checking Definition 12 (Correctness of translation) Let p be a predicate on models, p' be a predicate on systems. The predicate p' is a correct translation of p, if for all models m, we have that m |- p iff s D. (s |= (Sem(m) p’). Theorem Let P be a pattern and Spec(P) be a specification of the pattern. Suppose that Spec'(P) is a correct translation of Spec(P). For all models m, if Sem(m) Spec'(P) is true in FOL, then, for all systems s D, s |= m implies s |= Spec'(P).

Experiments v Specification of patterns: Ø v Translation: Ø v The specifications are translated into first order logic in LAMBDES syntax Experiment 1: checking specifications Consistency Ø Ø v 23 design patterns in Go. F book are specified in first order logic on models 23 specifications of patterns were checked for consistency with the axioms Results: all specification are consistent Experiment 2: Testing conformance checking ability Ø Ø Ø 23 designs represented in UML diagrams are created according to GOF; Each design is checked against all 23 patterns using LAMBDES Results: § 100% recognition of designs as instances of intended pattern § 22% of false positive recognitions (including time-out, which is 5%) v Experiment 3: Testing modelling tool’s correctness Ø Ø Ø 23 design created using Star. UML templates Each design is checked against all 23 patterns using LAMBDES Results: 61% is not recognised, Overall fault detecting rate: 81%

Conclusion and comparison v Separation of functional semantics from descriptive semantics can simplify the formal semantic definition of UML and it is scalable Applicable for all types of diagrams defined in meta-model uniformly Applicable to multiple views defined by multiple meta-models, and addressed the extendability issues Ø Addressed the issue due to flexibility in the uses of modelling language in different development context Ø Addressed the issue for different interpretation of modelling languages in different subject domains Ø Ø v Reasoning about models in first order logic can be feasible and useful in model drive software development Ø Ø Can be automated by tools such as LAMBDES + SPASS + Star. UML Can reason about properties that are not possible for semantics at object level, such as § The conformance of designs to patterns, § The validation of consistency constraints, § The consistency of meta-model, etc.

Future work v Further development of the axioms in second order predicate logic for functional semantics; v Theoretical analysis of the logic properties of the semantics definition Ø Ø Ø Soundness of the rules: yes Consistency of the rules: yes Completeness of the rules: § In what sense? § How to prove? v Case studies on reasoning about other properties of designs, such as Ø Ø Platform specific models, platform independence, etc. Transformation of models,

References 1. 2. 3. 4. 5. Hong Zhu, Ian Bayley, Lijun Shan and Richard Amphlett, Tool Support for Design Patterns in Model-Driven Development, submitted to ICSE 2009. Lijun Shan and Hong Zhu, A Formal Descriptive Semantics of UML, Proc. of ICFEM’ 08, 27 -31 October 2008 Kitakyushu. City, Japan. (In press) Ian Bayley and Hong Zhu, On the Composition of Design Patterns, Proc. of QSIC’ 08, IEEE CS Press, 12 -13 August, 2008, Oxford, UK. Ian Bayley and Hong Zhu, Specifying Behavioural Features of Design Patterns in First Order Logic, Proc. of COMPSAC’ 08, (Note: A full length version: Technical report TR-08 -01, Department of Computing, Oxford Brookes Univ. , Oxford, UK). Ian Bayley and Hong Zhu, Formalising Design Patterns in Predicate Logic, Proc. of SEFM’ 07, London, UK, Sept. 2007.