A-exam Cost Sharing and Approximation Martin Pál joint

A-exam Cost Sharing and Approximation Martin Pál joint work with Éva Tardos 12 Sep 03 Martin Pál: Cost sharing & Approx 1

Cost Sharing Internet: many independent agents • Not hostile, but selfish • Willing to cooperate, if it helps them 12 Sep 03 Martin Pál: Cost sharing & Approx 2

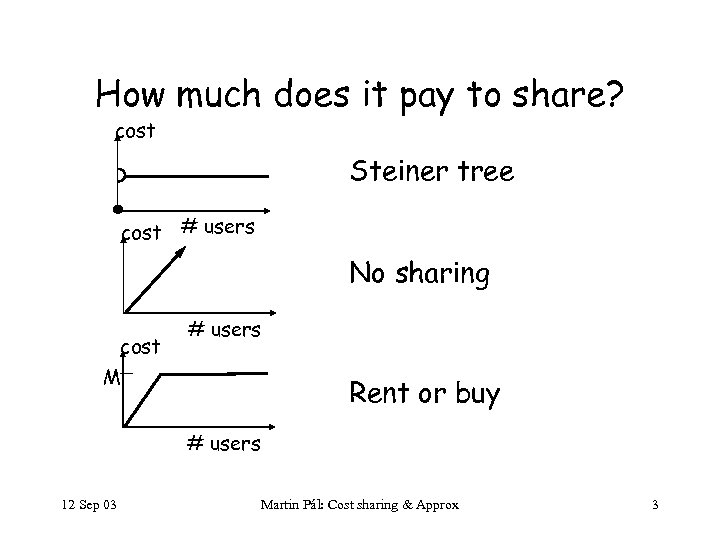How much does it pay to share? cost Steiner tree cost # users No sharing cost # users M Rent or buy # users 12 Sep 03 Martin Pál: Cost sharing & Approx 3

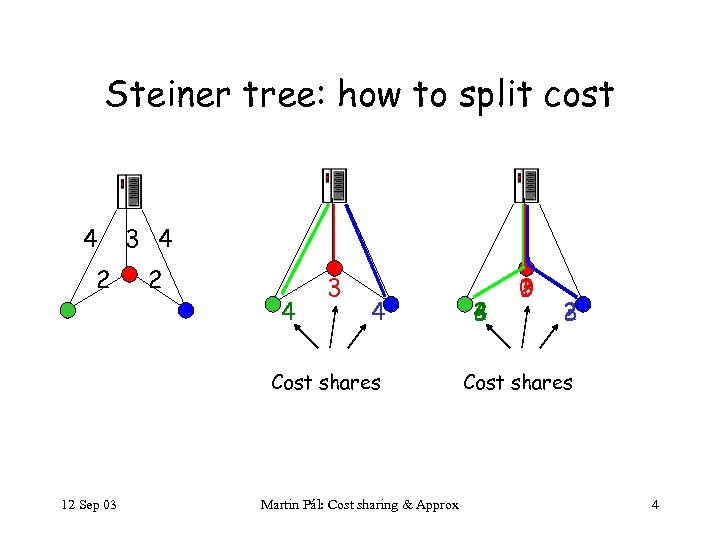Steiner tree: how to split cost 4 2 3 4 2 4 3 4 Cost shares 12 Sep 03 Martin Pál: Cost sharing & Approx 2 4 3 ? 3 0 ? 1 2 3 ? Cost shares 4

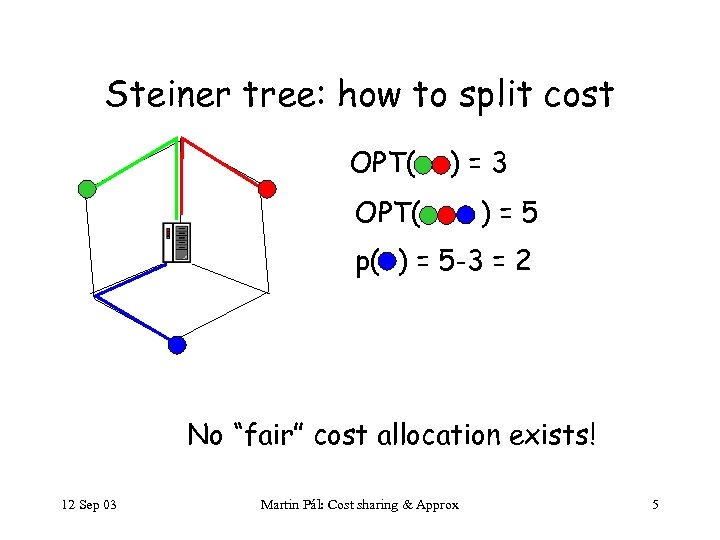Steiner tree: how to split cost OPT( )=3 OPT( )=5 p( ) = 5 -3 = 2 No “fair” cost allocation exists! 12 Sep 03 Martin Pál: Cost sharing & Approx 5

Utilities uj – utility of agent j Problem: users may not reveal true utilities p 1=15 =0 u 1’=5 u 1=25 $45 internet p 2=15 =22. 5 u 2=25 p 3=15 =22. 5 u 3=25 12 Sep 03 Martin Pál: Cost sharing & Approx 6

Cost sharing mechanism. . is a protocol/algorithm that • • requests utility uj from every user j selects the set S of people serviced builds network servicing S Computes the payment pj of every user j S 12 Sep 03 Martin Pál: Cost sharing & Approx 7

Desirable properties of mech’s • Σj S pj=c*(S) Σj S pj ≤ c*(S) • Only people in S pay Σj S pj ≥ c(S)/β (competitiveness) (budget balance) (voluntary participation) (approx. cost recovery) • No cheating, even in groups (group strategyproofness) • If uj high enough, j guaranteed to be in S (consumer sovereignity) 12 Sep 03 Martin Pál: Cost sharing & Approx 8

Cost sharing function ξ : 2 U U ℛ ξ(S, j) – cost share of user j, given set S • • Competitiveness: Σj S ξ(S, j) ≤ c*(S) Cost recovery: c(S)/β ≤ Σj S ξ(S, j) Voluntary particpiation: ξ(S, j) = 0 if j S Cross-monotonicity: for j S T ξ(S, j) ≥ ξ(T, j) 12 Sep 03 Martin Pál: Cost sharing & Approx 9

The Moulin&Shenker mechanism Let ξ : 2 U U ℛ be a cost sharing function. S U while unhappy users exist offer each j S service at price ξ(S, j) S S – {users j who rejected} output the set S and prices pj = ξ(S, j) Thm: [Moulin&Shenker]: ξ(. ) cross-monotonic mech. group strategyproof 12 Sep 03 Martin Pál: Cost sharing & Approx 10

Designing x-mono functions We construct cross-monotonic cost shares for two games: • Metric facility location game • Single source rent or buy game Facility location: competitive, recovers 1/3 of cost Rent or buy: competitive, recovers 1/15 of cost 12 Sep 03 Martin Pál: Cost sharing & Approx 11

Facility Location F is a set of facilities. D is a set of clients. cij is the distance between any i and j in D F. (assume cij satisfies triangle inequality) fi: cost of facility i 12 Sep 03 Martin Pál: Cost sharing & Approx 12

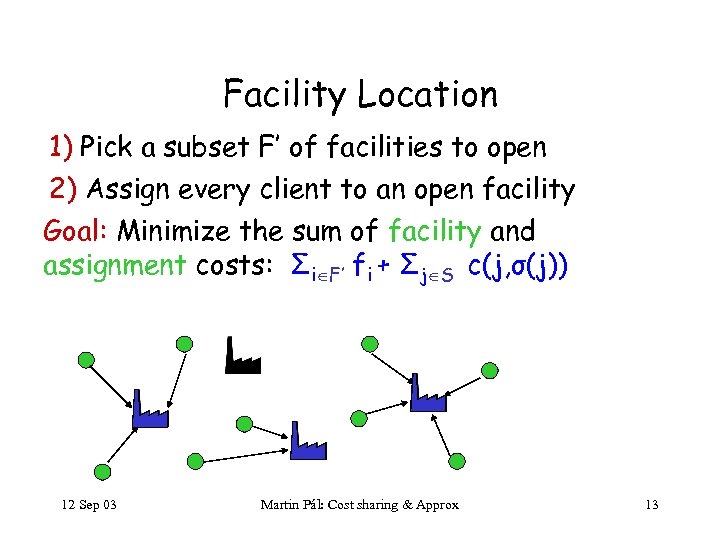Facility Location 1) Pick a subset F’ of facilities to open 2) Assign every client to an open facility Goal: Minimize the sum of facility and assignment costs: Σi F’ fi + Σj S c(j, σ(j)) 12 Sep 03 Martin Pál: Cost sharing & Approx 13

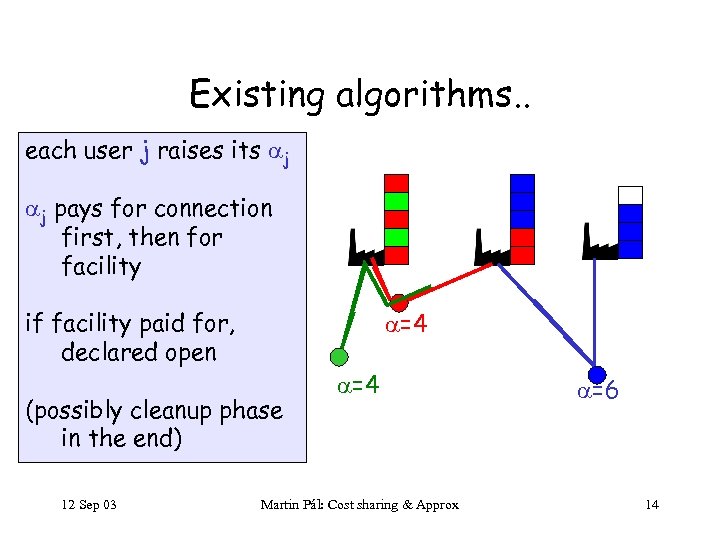Existing algorithms. . each user j raises its j j pays for connection first, then for facility if facility paid for, declared open =4 (possibly cleanup phase in the end) 12 Sep 03 =4 Martin Pál: Cost sharing & Approx =6 14

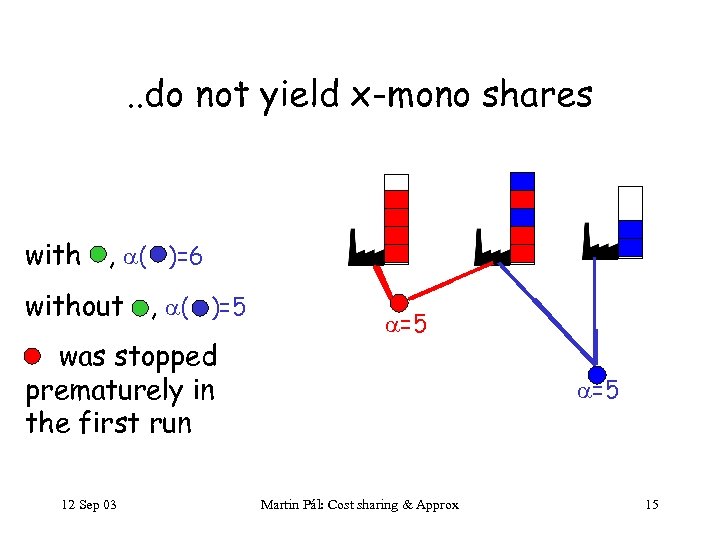. . do not yield x-mono shares with , ( )=6 without , ( )=5 was stopped prematurely in the first run 12 Sep 03 =5 =5 Martin Pál: Cost sharing & Approx 15

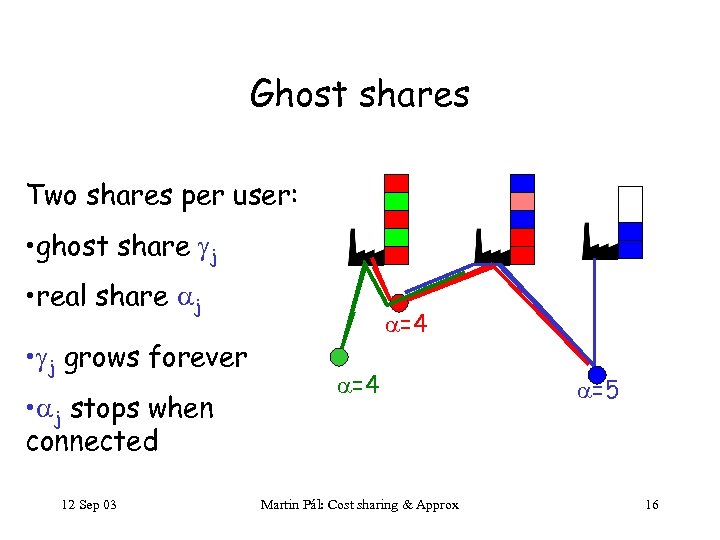Ghost shares Two shares per user: • ghost share j • real share j • j grows forever • j stops when connected 12 Sep 03 =4 =4 Martin Pál: Cost sharing & Approx =5 16

Easy facts Fact 1: cost shares j are cross-monotonic. Pf: More users opens facilities faster each j can only stop growing earlier. Fact 2 [competitiveness]: Σj S j ≤ c*(S). Pf: j is a feasible LP dual. Hard part: cost recovery. 12 Sep 03 Martin Pál: Cost sharing & Approx 17

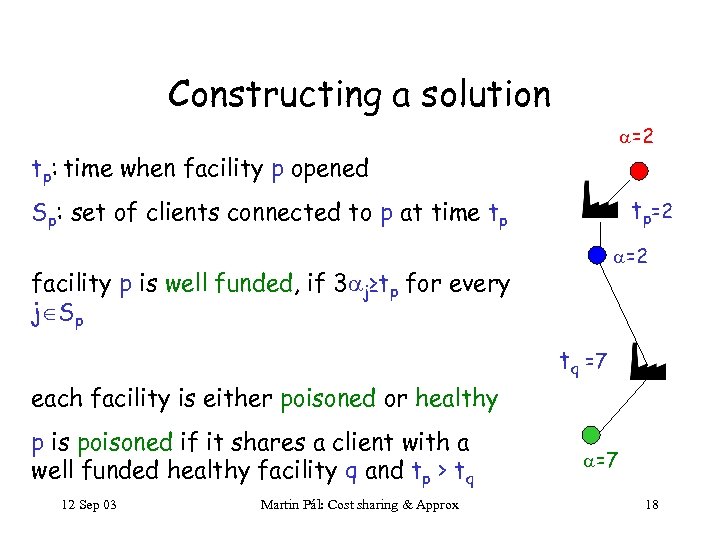Constructing a solution =2 tp: time when facility p opened tp=2 Sp: set of clients connected to p at time tp =2 facility p is well funded, if 3 j≥tp for every j Sp tq =7 each facility is either poisoned or healthy p is poisoned if it shares a client with a well funded healthy facility q and tp > tq 12 Sep 03 Martin Pál: Cost sharing & Approx =7 18

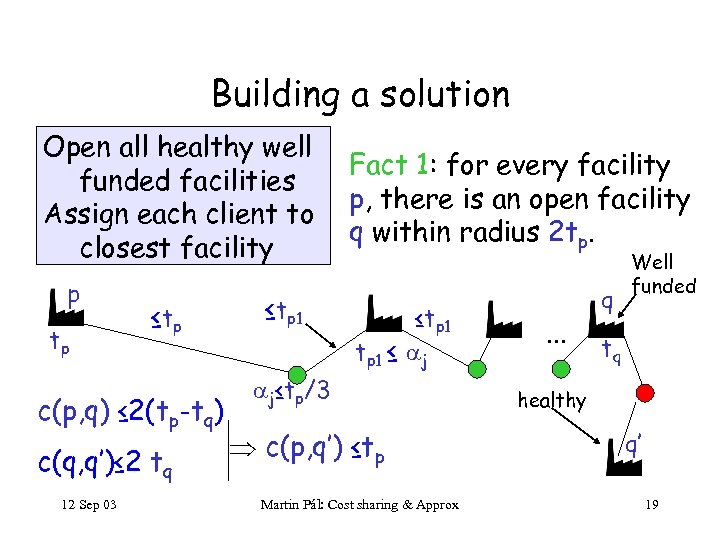Building a solution Open all healthy well funded facilities Assign each client to closest facility p tp ≤ tp c(p, q) ≤ 2(tp-tq) c(q, q’)≤ 2 tq 12 Sep 03 ≤tp 1 Fact 1: for every facility p, there is an open facility q within radius 2 tp. ≤tp 1 ≤ j j≤tp/3 c(p, q’) ≤tp Martin Pál: Cost sharing & Approx . . . q Well funded tq healthy q’ 19

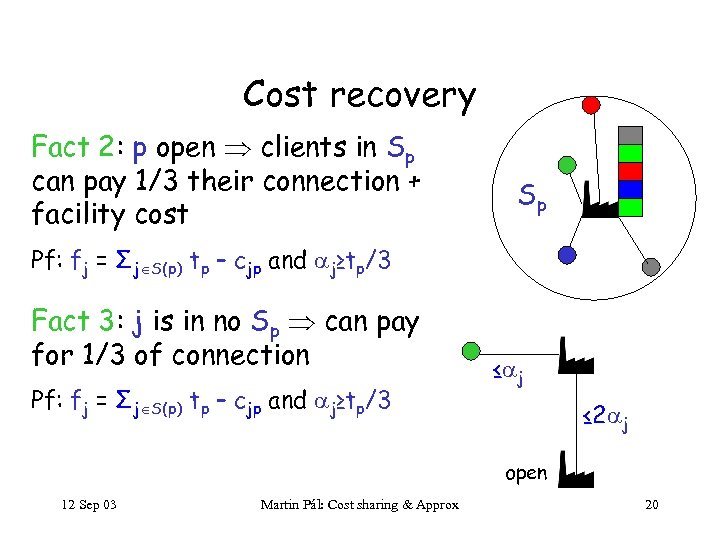Cost recovery Fact 2: p open clients in Sp can pay 1/3 their connection + facility cost Sp Pf: fj = Σj S(p) tp – cjp and j≥tp/3 Fact 3: j is in no Sp can pay for 1/3 of connection Pf: fj = Σj S(p) tp – cjp and j≥tp/3 ≤ j ≤ 2 j open 12 Sep 03 Martin Pál: Cost sharing & Approx 20

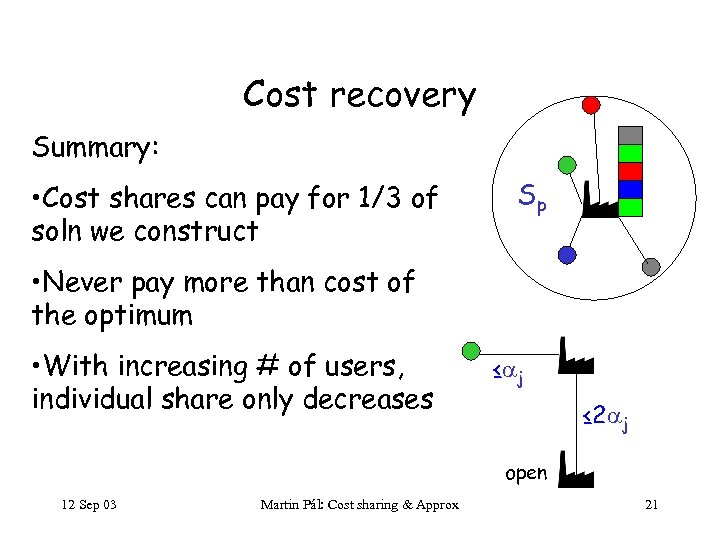Cost recovery Summary: • Cost shares can pay for 1/3 of soln we construct Sp • Never pay more than cost of the optimum • With increasing # of users, individual share only decreases ≤ j ≤ 2 j open 12 Sep 03 Martin Pál: Cost sharing & Approx 21

Single source rent or buy A set of clients D. A source node s. cij is the distance between any pair of nodes. (assume cij satisfies triangle inequality) 12 Sep 03 Martin Pál: Cost sharing & Approx 22

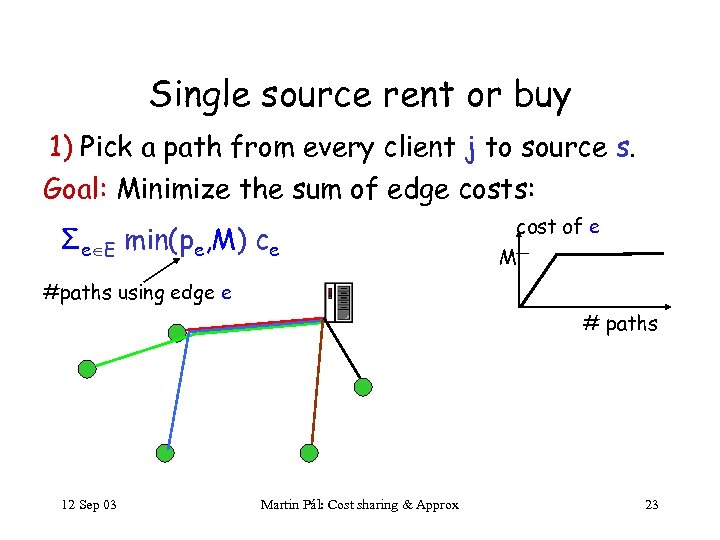Single source rent or buy 1) Pick a path from every client j to source s. Goal: Minimize the sum of edge costs: Σe E min(pe, M) ce cost of e M #paths using edge e # paths 12 Sep 03 Martin Pál: Cost sharing & Approx 23

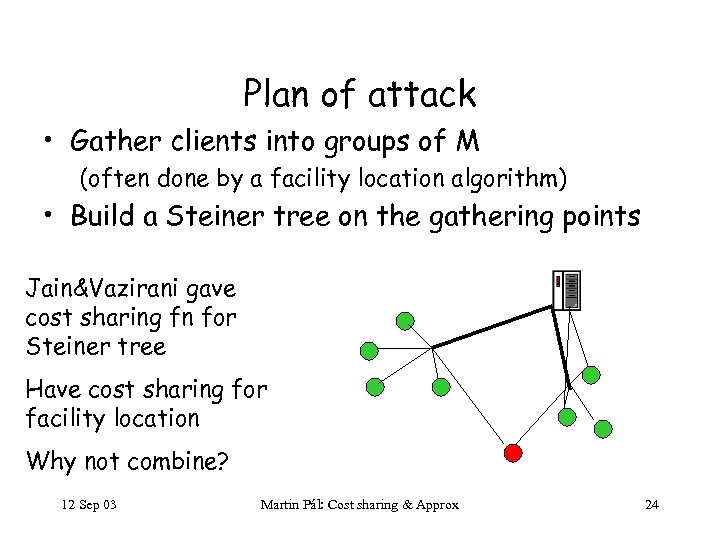Plan of attack • Gather clients into groups of M (often done by a facility location algorithm) • Build a Steiner tree on the gathering points Jain&Vazirani gave cost sharing fn for Steiner tree Have cost sharing for facility location Why not combine? 12 Sep 03 Martin Pál: Cost sharing & Approx 24

“One shot” algorithm • Generate gathering points and build a Steiner tree at the same time. • Allow each user to contribute only to the least demanding (i. e. largest) cluster he is connected to. not clear if the shares can pay for the tree 12 Sep 03 Martin Pál: Cost sharing & Approx 25

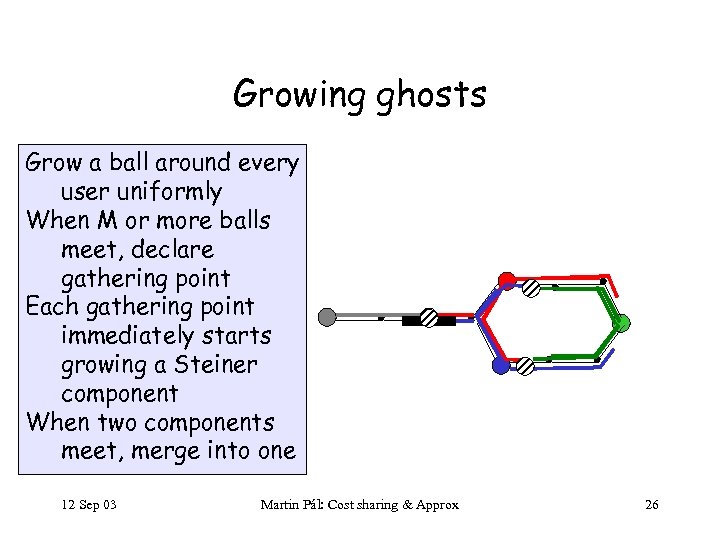Growing ghosts Grow a ball around every user uniformly When M or more balls meet, declare gathering point Each gathering point immediately starts growing a Steiner component When two components meet, merge into one 12 Sep 03 Martin Pál: Cost sharing & Approx 26

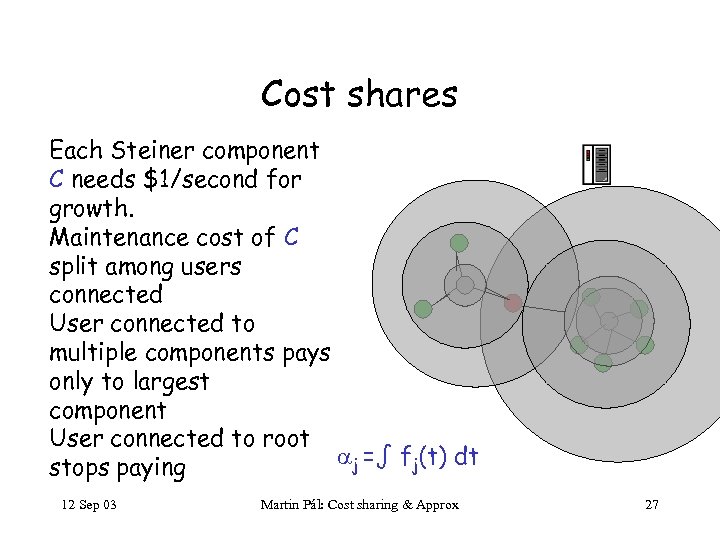Cost shares Each Steiner component C needs $1/second for growth. Maintenance cost of C split among users connected User connected to multiple components pays only to largest component User connected to root j =∫ fj(t) dt stops paying 12 Sep 03 Martin Pál: Cost sharing & Approx 27

Easy facts Fact: The cost shares j are cross-monotonic. Pf: More users causes more gathering points to open, more “area” is covered by Steiner clusters, clusters are bigger each j can only grow slower&stop sooner. Fact [competitiveness]: Σj S j ≤ 2 c*(S). Pf: LP duality. Again, cost recovery is the hard part. 12 Sep 03 Martin Pál: Cost sharing & Approx 28

Cost recovery To prove cost recovery, we must build a network. Steiner tree on all centers would be too expensive select only some of the centers like we did for facility location. Need to show to pay for the tree constructed. 12 Sep 03 Martin Pál: Cost sharing & Approx 29

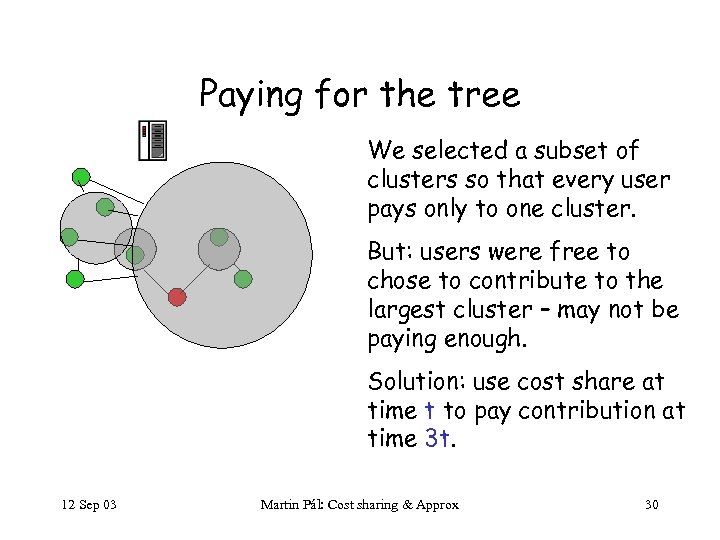Paying for the tree We selected a subset of clusters so that every user pays only to one cluster. But: users were free to chose to contribute to the largest cluster – may not be paying enough. Solution: use cost share at time t to pay contribution at time 3 t. 12 Sep 03 Martin Pál: Cost sharing & Approx 30

The last slide • x-mono cost sharing known only for 3 problems so far • Do other problems admit cross-mono cost sharing? • Covering problems? Steiner Forest? • Negative result: Set. Cover – no better than Ω(n) approx • Applications of cost sharing to design of approximation algorithms. Thank you! 12 Sep 03 Martin Pál: Cost sharing & Approx 31