A Core Course on Modeling Week 5 -Roles

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Contents Functional Models The 4 Categories Approach • Constructing the Functional Model • Input of the Functional Model: Category I • Output of the Functional Model: Category II • Limitations from Context: Category III • Intermediate Quantities: Category IV • Optimality and Evolution • Example / Demo • Summary • References to lecture notes + book • References to quiz-questions and homework assignments (lecture notes)

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Contents Functional Model: a model with ‘inputs’ mapped to ‘outputs’ Examples: purpose predict (1 ‘when …’): input = EMPTY; output = time point purpose predict (2 ‘what if …’): input = if-condition; output = what will happen purpose decide: input = decision; output = consequence purpose optimize: input = independent quantity; output = target (objective, …) purpose steer/control: input = perturbations; output = difference between realized and desired value purpose verify: input = EMPTY; output = succeed or fail (true or false) 2

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model The 4 -Categories Approach the printer’s dilemma: reading light, reading easy or reading much? light 3

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model The 4 -Categories Approach 4 the printer’s dilemma: reading light, reading easy or reading much? T = amount of text (char. -s) S = size of font (mm) P = number of pages (1) AP=TS 2, where A is a constant (standardized: A 4, A 5, …) A = area of one page (mm 2) T=amount of text P=number of pages S=size of font A=area of page …. but do we have S=f. S(T, P) or P=f. P(T, S) or T=f. T(P, S) ?

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model The 4 -Categories Approach T=amount of text P=number of pages S=size of font A=area of page the printer’s dilemma: reading light, reading easy or reading much? Unclarity about ‘what depends on what’ is a main source of confusion in functional models. 5

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model The 4 -Categories Approach 6 Elaborate each of the 3 possibilities Recollect: to go from conceptual model to formal model: T=amount of text P=number of pages S=size of font A=area of page • start with quantity you need for the purpose • put this on the to-do list • while the todo list is not empty: • take a quantity from the todo list • think: what does it depend on? • if depends on nothing substitute constant value (perhaps with uncertainty bounds) • else give an expression for it • if possible, use dimensional analysis • propose suitable mathematical expression • think about assumptions • in any case, verify dimensions • add newly introduced quantities to the todo list • todo list is empty: evaluate your model • check if purpose is satisfied; if not, refine your model

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model The 4 -Categories Approach 7 Case 1: reading light (P should be small) Quantity needed for purpose: P blue, underlined quantities appear underway to express pick P from to do list: P depends on C (=covered area), A what quantities depend on T=amount of text P=number of pages S=size of font A=area of page C=covered area Expression: P=C/A pick C from to do list: C depends on T, S Expression: C=TS 2 pick A from list constant pick T from list choose pick S from list choose

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model The 4 -Categories Approach 8 Case 2: reading easy (size of characters should be large) T=amount of text P=number of pages S=size of font A=area of page C=covered area L=letter area R=covered region Quantity needed for purpose: S pick S from to do list: S depends on L (= letter area = area of a single character) Expression: S = L pick L from to do list: L depends on R (= region covered by letters), T Expression: L = R / T pick R from to do list: R depends on P, A Expression: R = P * A pick A from list constant pick T from list choose pick P from list choose

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model The 4 -Categories Approach Case 3: reading much (amount of text should be large) T=amount of text P=number of pages S=size of font A=area of page C=covered area L=letter area R=covered region Z=area 1 letter Quantity needed for purpose: T pick T from to do list: T depends on R (= region covered by letters), Z (=surface of 1 char) Expression: T = R / Z pick R from to do list: R depends on A, P Expression: R = A * P pick Z from to do list: Z depends on S Expression: Z = S 2 pick A from list constant pick S from list choose pick P from list choose 9

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model The 4 -Categories Approach Reading light: 10 Reading easy: Reading much: we need P; P=C/A we need S; S= L we need T; T=R/Z quantities we need C=TS 2 L=R/T R=PA Z=S 2 A constant quantities from context T choose S choose P choose T=amount of text P=number of pages S=size of font A=area of page C=covered area L=letter area R=covered region Z=area 1 letter P choose intermediate quantities we can modify

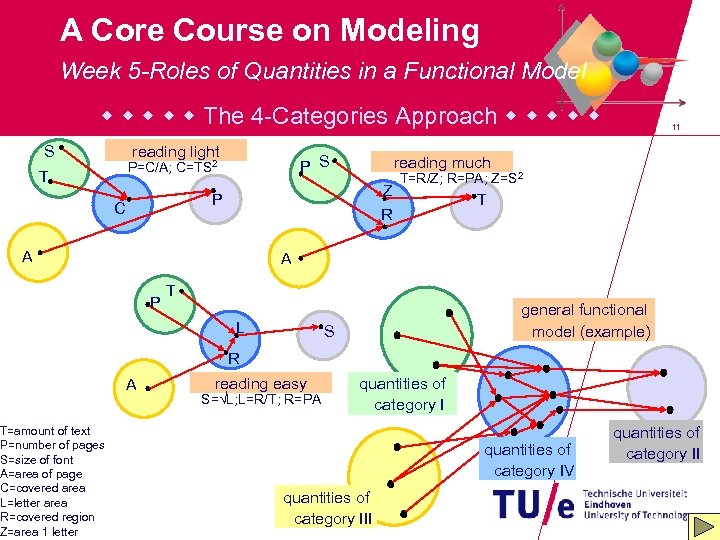A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model The 4 -Categories Approach reading light S P=C/A; C=TS 2 T Z T=R/Z; R=PA; Z=S 2 R A T=amount of text P=number of pages S=size of font A=area of page C=covered area L=letter area R=covered region Z=area 1 letter reading much P C 11 T A P T L general functional model (example) S R A reading easy S= L; L=R/T; R=PA quantities of category IV quantities of category III quantities of category II

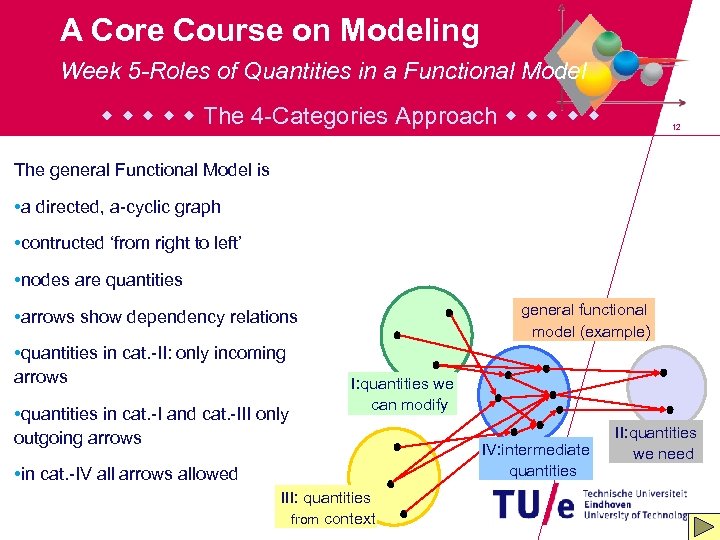A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model The 4 -Categories Approach 12 The general Functional Model is • a directed, a-cyclic graph • contructed ‘from right to left’ • nodes are quantities general functional model (example) • arrows show dependency relations • quantities in cat. -II: only incoming arrows • quantities in cat. -I and cat. -III only outgoing arrows I: quantities we can modify • in cat. -IV all arrows allowed III: quantities from context IV: intermediate quantities II: quantities we need

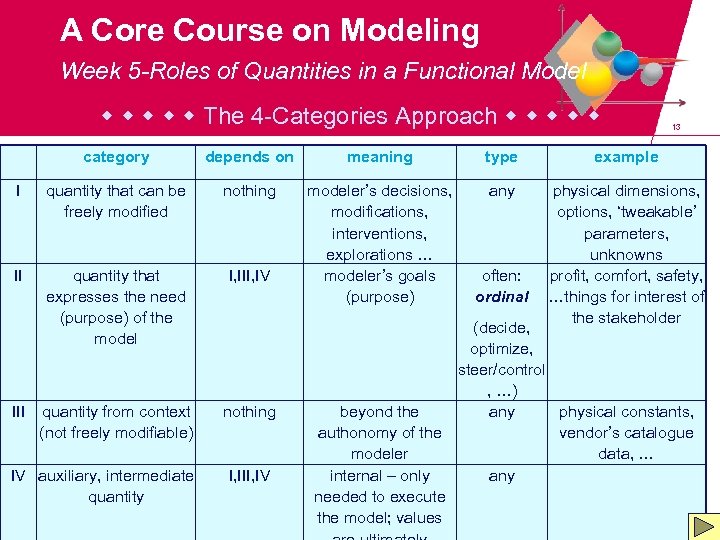A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model The 4 -Categories Approach 13 category depends on meaning type example I quantity that can be freely modified nothing any II quantity that expresses the need (purpose) of the model I, III, IV modeler’s decisions, modifications, interventions, explorations … modeler’s goals (purpose) physical dimensions, options, ‘tweakable’ parameters, unknowns profit, comfort, safety, …things for interest of the stakeholder quantity from context (not freely modifiable) nothing III IV auxiliary, intermediate quantity I, III, IV beyond the authonomy of the modeler internal – only needed to execute the model; values often: ordinal (decide, optimize, steer/control , …) any physical constants, vendor’s catalogue data, … any

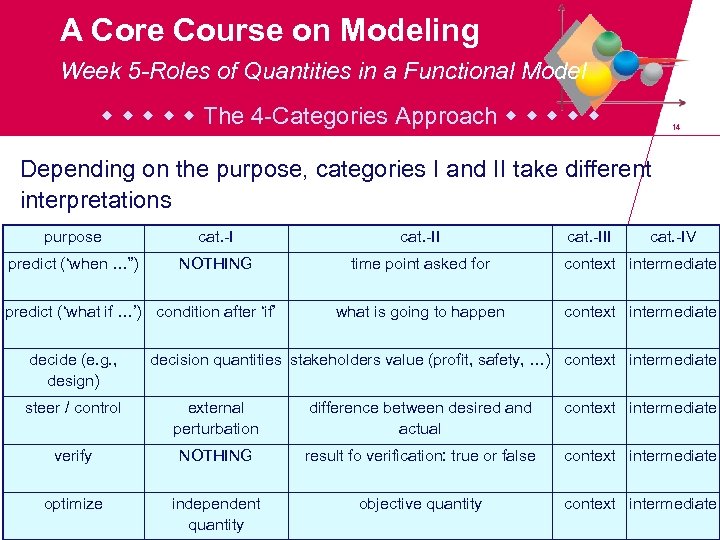A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model The 4 -Categories Approach 14 Depending on the purpose, categories I and II take different interpretations purpose cat. -II predict (‘when …”) NOTHING time point asked for context intermediate what is going to happen context intermediate predict (‘what if …’) condition after ‘if’ decide (e. g. , design) cat. -III cat. -IV decision quantities stakeholders value (profit, safety, …) context intermediate steer / control external perturbation difference between desired and actual context intermediate verify NOTHING result fo verification: true or false context intermediate optimize independent quantity objective quantity context intermediate

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Input of the Functional Model: Category I 15 The input of a functional model for design or exploration is often a complete collection of tuples. Each of these tuple has the same properties. Every property corresponds to one cat. -I quantity. The input of the FM is the cartesian product of the types of all cat. -I quantities. Example of a cat. -I space: the sandwiches of Subway with cat. -I quantities like ‘topping’, ‘add. Ons’, ‘type. Of. Bread’, ‘size’, ‘eat. In. Or. Take. Out’, …

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Input of the Functional Model: Category I 16 Category-I quantities correspond to independent, free decisions / modifications / explorations / …. The printer’s dilemma: T, S and P can not all be in category I, since TS 2/P=constant. T=amount of text P=number of pages S=size of font A=area of page C=covered area L=letter area R=covered region Z=area 1 letter • T, S: P may be too large to suit backpackers; • S, P: T may be too small to suit the curious reader; • P, T: S may be too small to suit senior readers. Choosing appropriate cat. -I quantities may require ‘cutting the Gordian knot’.

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Output of the Functional Model: Category II 17 The model function maps decisions (=values for cat. -I quantities) into their consequences for the stakeholders. Everything the model should yield for stakeholders, therefore is a condition on cat. -II quantities. Designing assumes that there is something we ‘want’, and therefore some present lack of stakeholders’ value: if not, there is no need for the designed artefact.

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Output of the Functional Model: Category II 18 1. Don’t include too many cat. -II quantities; 2. Include the right cat. -II quantities; 3. Cat. -II quantities for design etc. must be ordinal; 4. Cat. -II quantities must be SMART. remember: the design Be ware is a model, function of wrong Cat. -II quantitieswhen optimality. capturing E. g. , are This includes ‘soft’ aiming at used to assess house, if one insulating yourof the requirements ATBD the essentials(e. g. , is version of the optimize onalso other reasons for a psychology, another. ATBD (there are integral superior over on small amount of cat. -II quantities). costs, not just if economics, …) must Therefore they heating costs. possible. allow comparison.

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Output of the Functional Model: Category II Regarding SMART-ness: Even ‘hard’ quantities (e. g. , energy consumption, waste production, noise, …) often require non-trivial operationalization. example of operationalization: what is the energy consumption of a washing machine? • • • Joule/Hour? Joule/wash? Joule/(kg wash)? Joule/(kg removed dirt)? Joule/(lifetime of the piece of laundry)? Joule/(lifetime of the washing machine)? 19

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Output of the Functional Model: Category II Dilemma: many/few cat. -II quantities? consider the book printers’ example: three models reading light: cat. -I: S, T; cat. -II: P=TS 2/A; q. P=max(P-P 0, 0) reading easy: cat. -I: T, P; cat. -II: S= PA/T; q. S= - min(S-S 0, 0) reading much: cat. -I: P, S; cat. -II: T= PA/S 2; q. T= -min(T-T 0, 0) T=amount of text P=number of pages S=size of font A=area of page C=covered area L=letter area R=covered region Z=area 1 letter In each model, qi expresses something that is unwanted: the smaller qi, the better. The qi ‘punish’ unwanted behavior: penalty functions. If nr. pages is larger If point size larger than P 0, q. P is is less If text than Sis less than T , than 0. 0, q. S is larger 0 q. T is 0 than larger than 0 20

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Output of the Functional Model: Category II Different forms of penalties: • y=max(x, 0): it is bad if x>0 • y=|x|: it is bad if x is far from 0 • y= - min(x, 0): if is bad if x<0 • y=1/|x| or 1/( +|x|), >0: it is bad if x is close to 0 (use function selector to find suitable penalty!) 21

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Output of the Functional Model: Category II 22 Dilemma: many/few cat. -II quantities? Penalty function: ‘the smaller the better’. Every qi is a cat-II quantity, associated to a desired condition. Adding penalty functions: Q= iqi, to express that multiple conditions should hold simultaneously. For Q: ‘the smaller the better’. If separate qi non-negative, Q=0 is ideal. Penalty functions, like Chameleons, easily adapt to any desired condition. And they should be as small as possible, too.

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Output of the Functional Model: Category II 23 Dilemma: many/few cat. -II quantities? However: adding penalty functions may violate dimension constraints; adding penalty functions introduces (arbitrary) weights: Q= iaiqi, even if the ai are ‘omitted’; capitalization: express Q as a neutral quantity (e. g. , € or $). With possibly non-ethical consequences. Risks can be capitalized. But this would allow trading e. g. , preventive maintenance for insurance premiums!

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Output of the Functional Model: Category II Cat. -II quantities and requirements, desires, wishes Terminology: proposition=sentence that is true or false (‘cucumber is green’); predicate=proposition over a concept (‘is. Green(cucumber)=true’); requirement=predicate over some concept that needs to hold; desire=predicate over some concept that is appreciated. 24

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Output of the Functional Model: Category II 25 Cat. -II quantities and requirements, desires, wishes A third condition-type is the wish: ‘cat. -II quantity q should be as large (small) as possible’. This, however, is impossible to achieve: it would require all possible outcomes to compare with. Weaker version: Conditions ‘as large (small) as possible’ can not be realized: we have ‘q should approximate the max (min) to restrict the search to the cat. -I space. as achievable in the cat. -I space’.

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Output of the Functional Model: Category II 26 Cat. -II –space and dominance Cat. -I space contains all possible configurations of the modeled system; This space is much too large for systematic exploration, or finding ‘good’ solutions; ‘The best’ solution will, in general not exist since various cat. -II quantities cannot be compared (e. g. , different dimensions); So: we must try to prune cat. -I space. Cat. -I space, for all but trivial problems, is by far too large to systematically explore for man … , much like physical space.

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Output of the Functional Model: Category II 27 Cat. -II –space and dominance Assume cat. -II quantities are ordinals: Every axis in cat. -II space is ordered; concept C 1 dominates C 2 iff, for all cat. -II quantities qi, C 1. qi is better than C 2. qi; ‘Being better’ may mean ‘<‘ (e. g. , waste) or ‘>’ (e. g. , profit); If C 1 dominates C 2, this no longer needs to be true if we add a further cat. -II quantity; The more cat. -II quantities, the fewer dominated solutions. ‘Dominance’ means: being better in all respects. For design, this means: the artefact being better w. r. t. all (properties of all) stakeholders’ values.

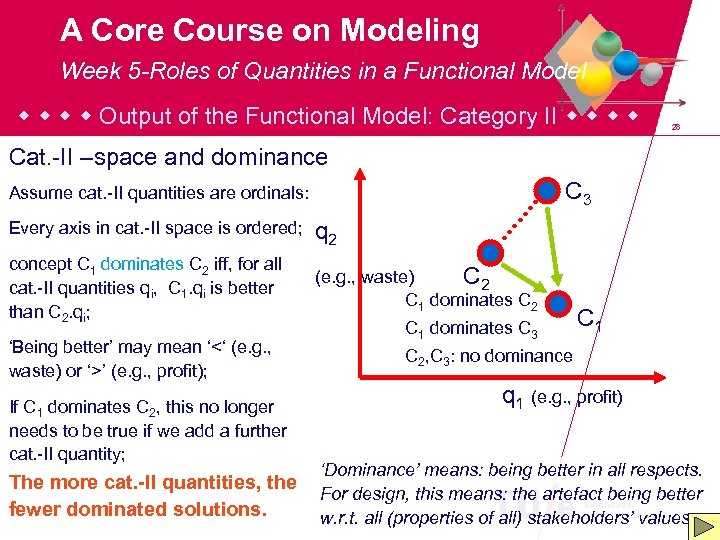A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Output of the Functional Model: Category II 28 Cat. -II –space and dominance C 3 Assume cat. -II quantities are ordinals: Every axis in cat. -II space is ordered; q 2 concept C 1 dominates C 2 iff, for all cat. -II quantities qi, C 1. qi is better than C 2. qi; (e. g. , waste) C 2 C 1 dominates C 2 ‘Being better’ may mean ‘<‘ (e. g. , waste) or ‘>’ (e. g. , profit); If C 1 dominates C 2, this no longer needs to be true if we add a further cat. -II quantity; The more cat. -II quantities, the fewer dominated solutions. C 1 dominates C 3 C 1 C 2, C 3: no dominance q 1 (e. g. , profit) ‘Dominance’ means: being better in all respects. For design, this means: the artefact being better w. r. t. all (properties of all) stakeholders’ values.

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Output of the Functional Model: Category II 29 Cat. -II –space and dominance Only non-dominated solutions are relevant dominance allows pruning cat. -I space; Since nr. non-dominated solutions is smaller with more cat. -II quantities, nr. of cat. -II quantities should be small; For 2 cat. -II quantities, the cat. -II space can be visualized; Dominance is defined, however, for any nr. cat. -II quantities. Dominance is a simple criterion to prune cat. -I space. We only need to consider nondominated solutions. The relative reduction is larger with fewer cat. -II quantities.

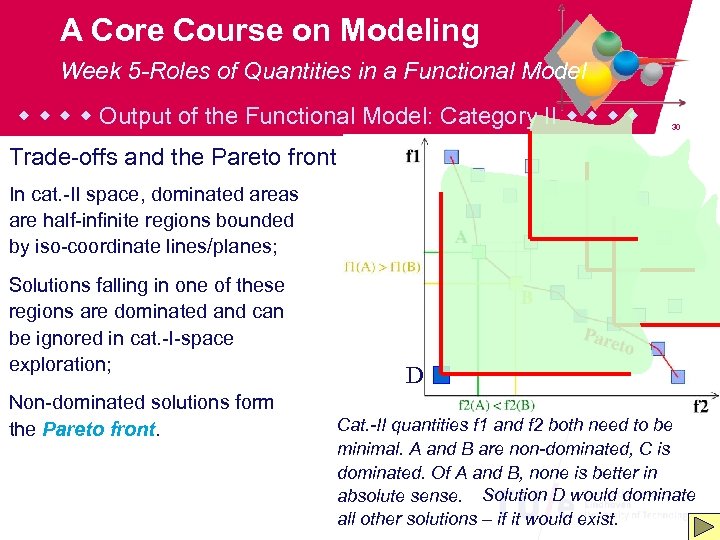A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Output of the Functional Model: Category II 30 Trade-offs and the Pareto front In cat. -II space, dominated areas are half-infinite regions bounded by iso-coordinate lines/planes; Solutions falling in one of these regions are dominated and can be ignored in cat. -I-space exploration; Non-dominated solutions form the Pareto front. D Cat. -II quantities f 1 and f 2 both need to be minimal. A and B are non-dominated, C is dominated. Of A and B, none is better in absolute sense. Solution D would dominate all other solutions – if it would exist.

A Core Course on Modeling Bonus: when we apply a monotonous Week 5 -Roles of Quantities in to some or all cat. -IIModel mapping a Functional quantities, the collection non-dominated solutions stays the same. Example: it Output of the Functional Model: Category II doesn’t matter if a penalty function is |a -b| Trade-offs and the Pareto front or (a-b)2 Relevance of Pareto-front: 31 direction of absolute deterioration • it bounds the achievable part of cat. -II space; • solutions not on the Pareto front can be discarded; • it exists for any model function, although in general it can only be approximated by a disjoint collection of solutions; • if (part of) it is smooth, it defines two directions in cat. -II space: the direction of absolute improvement / deterioration, and the plane perpendicular to this direction which is tangent to the Pareto front and represents local trade-off relationships between cat. -II quantities. tan g ent to t h ep are to- fro nt: tra dedirection of absolute improvement offs Cat. -II quantities f 1 and f 2 both need to be minimal. A and B are non-dominated, C is dominated. Of A and B, none is better in absolute sense.

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Limitations from Context: Category III 32 In order to evaluate a model function, we may need quantities, not in category I; These are category-III quantities from the model context, not modifiable by the modeler; Example: legislature, demography, physics, economy, vendor catalogues, human conditions, … Challenge the demarcation between cat. -I and cat. –III for innovative design. Example: when designing thermal house insulation, heat leakage through the windows occurs in the design function. If the window area is in cat. -I, zero-sized windows might be optimal. Else the window size is in cat. -III.

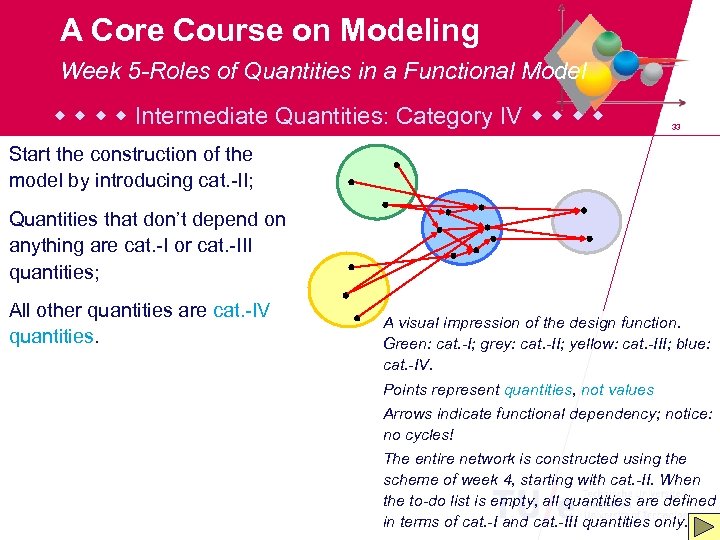A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Intermediate Quantities: Category IV 33 Start the construction of the model by introducing cat. -II; Quantities that don’t depend on anything are cat. -I or cat. -III quantities; All other quantities are cat. -IV quantities. A visual impression of the design function. Green: cat. -I; grey: cat. -II; yellow: cat. -III; blue: cat. -IV. Points represent quantities, not values Arrows indicate functional dependency; notice: no cycles! The entire network is constructed using the scheme of week 4, starting with cat. -II. When the to-do list is empty, all quantities are defined in terms of cat. -I and cat. -III quantities only.

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Optimality and Evolution 34 Our mission is to find ‘good’ or even ‘best’ concepts in cat. -I space. Mathematical optimization regards singlevalued functions; Approach typically imitates a mountaineer climbing to the top of a (single-valued) mountain; This would correspond to the situation of a single cat. -II quantity, or all cat. -II quantities lumped; We seek something more generic. Mathematical optimization attempts to find a local or even global extreme of a single-valued function. Most methods work by iteration, i. e. , following a mountaineer on its route to the top. This approach would only apply to model functions in case of 1 cat. -II quantity.

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Approximating the Pareto Front 35 Idea (Eckart Zitzler): combine Pareto and Evolution. Main features of evolution: • genotype encodes blueprint of individual (‘cat. -I’); • genotype is passed over to offspring; • new individual: genotype phenotype, determining its fitness (‘cat. -II’); • variations in genotypes (mutation, cross-over) cause variation among phenotypes; • fitter phenotypes have larger change of surviving, procreating, and passing their genotypes on to next generation. Evolution as a principle for development may occur in biological and artificial systems alike

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Approximating the Pareto Front 36 Idea (Eckart Zitzler): combine Pareto and Evolution. ‘Strength’ (hence ‘SPEA’) is a property of an ATBD, Issues to resolve: derived from the cat. -II quantities, • How to start population of random individuals indicating how (tuples of values for cat. -I quantities); few it is dominated by, i. e. how fit it is. • How to define fitness fitter when dominated by fewer; Charles Darwin • Next generation preserve non-dominated ones; complete population with mutations and crossing-over; • Convergence if Pareto front no longer moves. Pareto and Darwin: the dynamic duo of optimal design (under direction of E. Zitzler)

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Approximating the Pareto Front 37 Idea (Eckart Zitzler): combine Pareto and Evolution. Caveats: Pareto-Genetic is not perfect • If the fraction dominated concepts is too large, evolution ceases to make progress; • If there broad niches, finding individuals in a narrow niche may be problematic; • Approximations may fail to get anywhere near theoretical best Pareto front. (No guarantee that analytical alternatives exist) DON’T use Pareto-Genetic if guarantee for optimal solution is required. Charles Darwin Nothing is perfect. There are cases when Pareto-genetic optimization does not meet its target, or when it should not be used.

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Approximating the Pareto Front demo 38 Charles Darwin

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Approximating the Pareto Front 39 Idea (Eckart Zitzler): combine Pareto and Evolution. If anything else fails: • Complementary approach: local optimization (to be applied on all elements of the Pareto-front separately); Charles Darwin • Split cat. -I space in sub spaces if model function behaves different in different regimes (e. g. , too much cat. -I If anything else fails, there are few brute-force methods that may help in difficult situations freedom may lead to bad evolution progress); • Temporarily fix some cat. -IV quantities (pretend that they are in category-III).

A Core Course on Modeling Week 5 -Roles of Quantities in a Functional Model Summary • functional model helps distinguish input (choice) and output (from purpose); • Building a functional model as a graph shows roles of quantities. These are: • Cat. -I : free to choose; • Models for (design) decision support: the notion of design space; • Choice of cat. -I quantities: no dependency-by-anticipation; • Cat. -II : represents the intended output; • The advantages and disadvantages of lumping and penalty functions; • The distinction between requirements, desires, and wishes; • The notion of dominance to express multi-criteria comparison; Pareto front; • Cat. -III : represents constraints from context; • Cat. -IV : intermediate quantities; • For optimization: use evolutionary approach; • Approximate the Pareto front using the SPEA algorithm; • Local search can be used for post-processing. 40