A Core Course on Modeling Week 4 -The

A Core Course on Modeling Week 4 -The Function of Functions Contents • What is a Formal Model? • A Practical Route to Formal Models • Example 1: The Detergent Problem • Example 2: The Chimney Sweepers Problem • Example 3: The Peanut Butter Problem • The relation wizard • The function selector • Summary • References to lecture notes + book • References to quiz-questions and homework assignments (lecture notes)

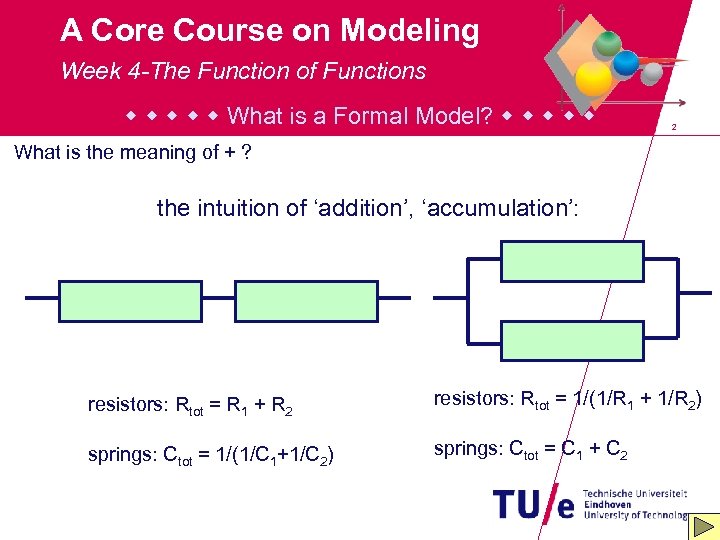A Core Course on Modeling Week 4 -The Function of Functions What is a Formal Model? 2 What is the meaning of + ? the intuition of ‘addition’, ‘accumulation’: resistors: Rtot = R 1 + R 2 resistors: Rtot = 1/(1/R 1 + 1/R 2) springs: Ctot = 1/(1/C 1+1/C 2) springs: Ctot = C 1 + C 2

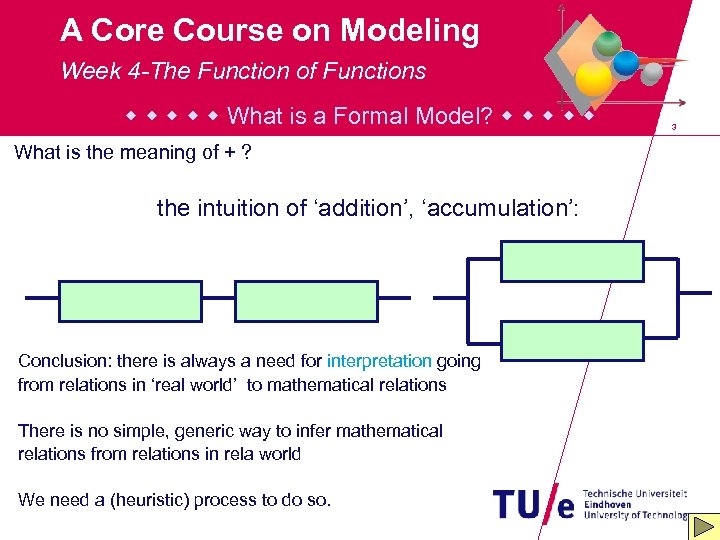A Core Course on Modeling Week 4 -The Function of Functions What is a Formal Model? What is the meaning of + ? the intuition of ‘addition’, ‘accumulation’: Conclusion: there is always a need for interpretation going from relations in ‘real world’ to mathematical relations There is no simple, generic way to infer mathematical relations from relations in rela world We need a (heuristic) process to do so. 3

A Core Course on Modeling Week 4 -The Function of Functions A Practical Route to Formal Models 4 Heuristics to arrive at formal expressions: In a conceptual model, properties are • meaningful names General scheme: start with always part of a concept the quantitiy Everytime when introducing a new needed for your purpose, and try to express (‘my. Car. wheel. diameter’). In a formal • chain of dependencies When seeking a mathematical list. When a this in quantity, add it to the todo expression, other quantities model, Often values expressed intoquantities properties may be ‘just’ in something quantityuseneed guessing. If you can • if possible, is dimensional considerations • todo-list Sometimes, there are • in theknown (= possible people, two orthat simplest a value form let involve a number of with names more (‘my. Car. Wheel. Diameter) or another them to find needed expression your complete and … A model never model. (part) This guessroutes to take isof the todo(a) a independently. off gives list. may be as few as possibleyou have your first expression), Once it • with meaningfully abbreviated given its assumptions • dimensional analysis fully estimate if there are no accurate. and with Implement them all, But, compare more • … but at least todo list running, you can: When the verify expression (‘m. CWh. D’). accurateversion is empty, model’s • such thatthe results. Thewritten as function the analysis is (b) be in results systematicpurpose, it spread complete errors dimensional quantityand can an idea of theis • wisdom of the crowds first version is ready. • use it to find out which of the other clue to the reliability of the a quantities variation. and accurate enough. (See • … evenachievable outcome. of yourcheck are if this may require inventing units uncertainties chapter 6. ) Regularly inputs if • two models is better than one model • continue with the arguments ofunknown to get Otherwise: your purpose is met. function try to most the and dimensions. therelatedominant try these more accurate if values to values you (and your friends) • when is a model good enough? necessary may know. • Baron von Münchhausen • find out which modifications could be worthwhile

A Core Course on Modeling Week 4 -The Function of Functions The Detergent Problem “What is the total amount of detergent annually dumped in the Environment in the Netherlnds? 5

A Core Course on Modeling Week 4 -The Function of Functions The Detergent Problem relations dimensions assumptions am. An. Det. Dmp = [kg / year] = nr. An. Wshs * det. PWsh nr. An. Wshs = [wash / year] * [kg / wash] [wash / year] = nr. An. Wshs. PFam * nr. Fam. IH = Washing laundry is the only way detergent gets into the environment No institutional laundry washing, only families [wash / (fam *year)] * [fam] = nr. PIH / nr. PPFam [people] / [people / fam] Everybody belongs to exactly one family: families are disjoint nr. PIH = 17 0. 5 million [people] common knowledge nr. PPFam = 2. 2 0. 2 [people/fam] am. An. Det. Dmp nr. An. Wshs det. PWsh nr. An. Wshs. PFam nr. Fam. IH nr. PPFam todo list is empty model is ready wisdom of the crowds det. PWsh = 0. 17 0. 03 [kg / wash] todo public domain nr. An. Wshs. PFam = 100 20 [wash / year] 6 wisdom of the crowds Det: detergent; An: annual; Wsh: wash; Fam: family; P: people; am: amount; Dmp: dump

A Core Course on Modeling Week 4 -The Function of Functions The Detergent Problem 7 This type of model is a ‘thumbnail calculation’: • OK for quick order of magnitude estimations • Uses straightforward substitutions, only based on dimension analysis • Work with intervals to get an impression of the variation of the answers (143 67 M; correct value according to various sites such as http: //wiki. watmooi. nl/pages/Wassen_en_onderhoud is 150 M kg) • Purpose: pub quizzes, trivial pursuit, … a. k. a. ‘sledgehammer estimation’

A Core Course on Modeling Week 4 -The Function of Functions The Detergent Problem About accuracy model: outcome = function of inputs y=f(x 1, x 2, …) y= f/ x 1 + f/ x 2 + … So: | y|=| f/ x 1| | x 1| + | f/ x 2| | x 2| + … This is a very pessimistic upperbound: all quantities need to conspire to give worst case deviation. In chapter 6, we will get a more realistic estimate. 8

A Core Course on Modeling Week 4 -The Function of Functions The Chimney Sweepers Problem “How many chimney sweepers work in Amsterdam? ” 9

A Core Course on Modeling Week 4 -The Function of Functions The Chimney Sweepers Problem relations nr. Ch. Sw. IA = nr. Ch. IA * nr. Sw. PCh nr. Ch. IA = nr. Ch. PFam * nr. Fam. IA = nr. PIA / nr. PPFam dimensions [Sw / A] = [Ch / A] * [SW / Ch] [Ch / A] = [Ch / Fam] * [Fam / A] = [P / A] / [P / Fam] 10 assumptions todo Amsterdam ch. -sweepers sweep Amsterdam chimneys only nr. Ch. Sw. IA nr. Ch. IA nr. Sw. PCh ch. -sweepers sweep only chimneys on family houses nr. Ch. PFam nr. Fam. IA nr. PPFam is the same everywhere (does not depend on ‘Amsterdam’) nr. PIA = 790000 [P] common knowledge nr. PPFam = 2. 2 0. 2 [P/Fam] public domain nr. Ch. PFam (= 1/nr. Fam. PCh) =0. 1 0. 02 [Ch/Fam] wisdom of the crowds Sw=sweeper; Ch=chimney; A=Amsterdam; Fam=Family; P=people; Se=Service;

To find an expression for nr. Sw. PCh, ask: ‘what links the nr of sweepers to the nr chimneys? ’. Answer: sweepers service chimneys. ‘How many services’ (1) relates to the capacity (=available resource) of a sweeper, and (2) to the need of a chimney (=needed resource). Here, ‘resource’=time. The capacity of a sweeper is expressed in the time he works ([Sw*year]); The ‘need’ of a chimney is therefore expressed ([Ch*year]). A Core Course on Modeling Week 4 -The Function of Functions The Chimney Sweepers with dimension time. To that are Problem verify units Notice: two different units, both relations 11 consistent, substitute back into expressions for nr. Sw. PSe and nr. Sw. PCh: check that all units multiply and divide to produce the correct final result. dimensions assumptions todo In this case: nr. Sw. PCh=time. P 1 Se * nr. Se. PCh / time. P 1 Sw has unit ‘sweeper / chimney’ which is correct. [Sw / Ch]– = Introduce time to nr. Ch. Sw. IA nr. Sw. PCh = nr. Sw. PSe * nr. Se. PCh nr. Sw. PSe = [Sw*year/Se] * [Se/(Ch*year)] [Sw * year / Se] = time. P 1 Se / time. P 1 Sw [hour / Se] / [hour / (Sw*year)] time. P 1 Se = 2 0. 25 hour / Se time. P 1 Sw = 1200 100 hour / Sw * year) nr. Se. PCh = 1 Se /( Ch * year) todo list is empty model is ready associate sweeper’s capacity to chimney’s need nr. Ch. IA nr. Sw. PCh assume average times nr. Ch. PFam nr. Fam. IA nr. PPFam nr. Sw. PSe nr. Se. PCh time. P 1 Se time. P 1 Sw (i. e. , no season influences etc. ) wisdom of the crowds work year = 1600 hours insurance requirement but what does it mean ? NOTHING, since we formulated no purpose Sw=sweeper; Ch=chimney; A=Amsterdam; Fam=Family; P=people; Se=Service;

A Core Course on Modeling Week 4 -The Function of Functions The Chimney Sweepers Problem 12 What purposes could we think of: are there at least 300 Chimney Sweepers so that we can begin a professional journal? so: we only need to know if Nr. Ch. Sw. IA > 300 are there less than 50 Chimney Sweepers so that we can have next year’s Ch. Sw convention meeting in the Restaurant ‘the Swinging Sweeper? ’ so: we only need to know if Nr. Ch. Sw. IA <50 are there about as many Chimney Sweepers as there are Sewer Cleaners so that we can form efficient ‘Chimney and Sewage Control and Service Units’? so: we only need to know if Nr. Ch. Sw. IA is between 50 and 60… … each purposes different challenges / allows different approximations in our model. but what does it mean ? NOTHING, since we formulated no purpose

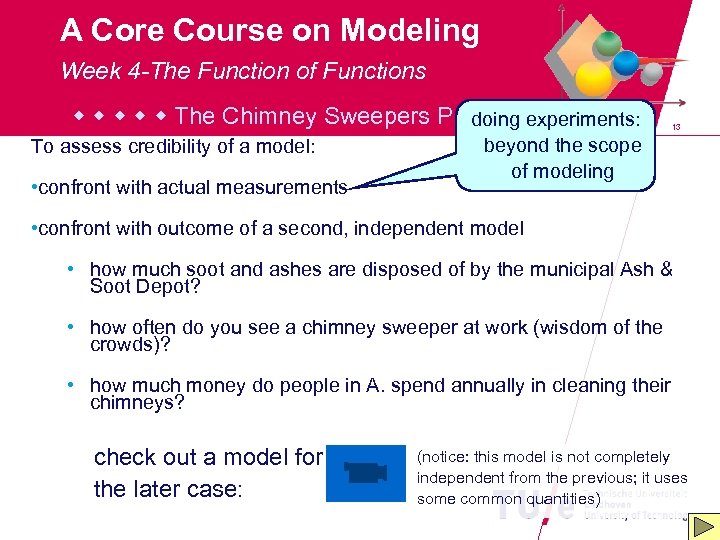A Core Course on Modeling Week 4 -The Function of Functions The Chimney Sweepers Problemexperiments: doing To assess credibility of a model: • confront with actual measurements 13 beyond the scope of modeling • confront with outcome of a second, independent model • how much soot and ashes are disposed of by the municipal Ash & Soot Depot? • how often do you see a chimney sweeper at work (wisdom of the crowds)? • how much money do people in A. spend annually in cleaning their chimneys? check out a model for the later case: (notice: this model is not completely independent from the previous; it uses some common quantities)

A Core Course on Modeling Week 4 -The Function of Functions The Chimney Sweepers Problem 14 Thusfar, all mathematical relations were obtained via dimension analysis. Dimensions are more generic than just SI dimensions/units. Dimensional analysis often works for models of a particular form: y = x 1 n 1 * x 2 n 2 * x 3 n 3 … = i xini, where (integer) ni can be both larger and smaller than 0. How to go about when other forms are needed?

A Core Course on Modeling Week 4 -The Function of Functions The Peanut Butter Problem “How to get rich by selling a new brand of peanut butter? ” PB 15

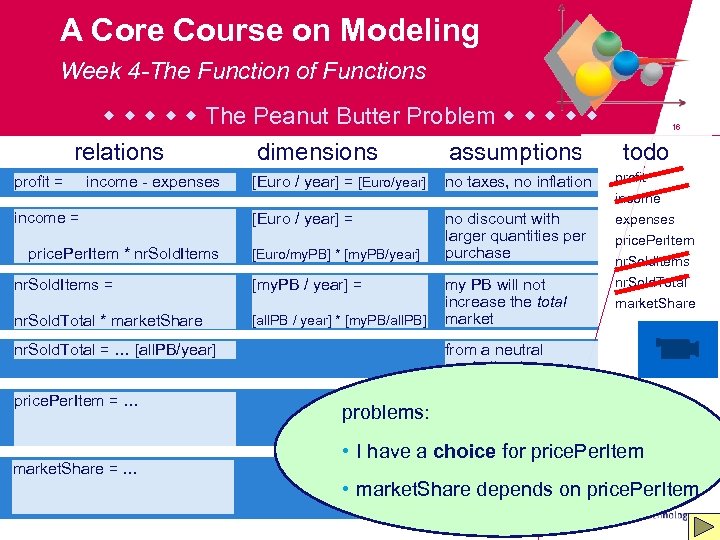A Core Course on Modeling Week 4 -The Function of Functions The Peanut Butter Problem relations dimensions assumptions profit = income - expenses income = price. Per. Item * nr. Sold. Items [Euro / year] = [Euro/year] no taxes, no inflation [Euro / year] = no discount with larger quantities per purchase [Euro/my. PB] * [my. PB/year] nr. Sold. Items = [my. PB / year] = nr. Sold. Total * market. Share [all. PB / year] * [my. PB/all. PB] market. Share = … todo profit income expenses price. Per. Item nr. Sold. Items nr. Sold. Total market. Share from a neutral marketing bureau nr. Sold. Total = … [all. PB/year] price. Per. Item = … my PB will not increase the total market 16 problems: • I have a choice for price. Per. Item • market. Share depends on price. Per. Item

A Core Course on Modeling Week 4 -The Function of Functions The Peanut Butter Problem market. Share Approach 1: glass box (glass jar …; -): ? 1 0 price. Per. Item problems: • I have a choice for price. Per. Item • market. Share depends on price. Per. Item 17

A Core Course on Modeling If something gets more market. Share A market sharechance people it expensive, the cannot be <0; will Week 4 -The Function of Functions If somethingbut only if it creates could decreases sufficiently be >1 gets buy it If something gets sufficiently expensive, nobody will buy it additional request It would need potentially cheap, a glass The Peanut Butter Problem every box model of customers’ brains willderive 18 this interested customer to buy (or dependency from first principles Approach 1: glass box (glass jar …; -): get!) it 1 0 What mechanism determines market. Share(price. Per. Item)? • monotonically decreasing • between 0 and 1 • asymptote: market. Share 0 if price. Per. Item • asymptote: market. Share 1 if price. Per. Item - • what sort of mathematical dependency ? ? ? price. Per. Item problems: • I have a choice for price. Per. Item • market. Share depends on price. Per. Item

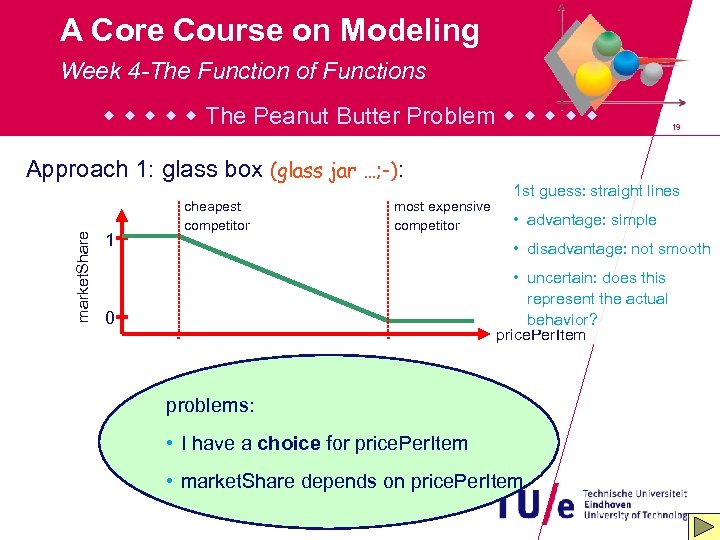A Core Course on Modeling Week 4 -The Function of Functions The Peanut Butter Problem market. Share Approach 1: glass box (glass jar …; -): 1 cheapest competitor most expensive competitor 19 1 st guess: straight lines • advantage: simple • disadvantage: not smooth • uncertain: does this represent the actual behavior? price. Per. Item 0 problems: • I have a choice for price. Per. Item • market. Share depends on price. Per. Item

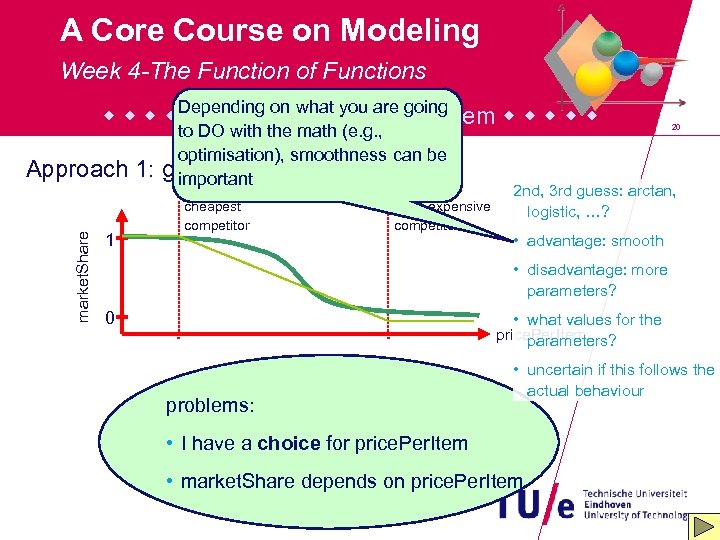A Core Course on Modeling Week 4 -The Function of Functions Depending on what Butter going The Peanut you are Problem market. Share Approach 1: 1 to DO with the math (e. g. , optimisation), smoothness can be glass box (glass jar …; -): important cheapest competitor most expensive competitor 20 2 nd, 3 rd guess: arctan, logistic, …? • advantage: smooth • disadvantage: more parameters? 0 • what values for the price. Per. Item parameters? problems: • uncertain if this follows the actual behaviour • I have a choice for price. Per. Item • market. Share depends on price. Per. Item

A Core Course on Modeling Week 4 -The Function of Functions The Peanut Butter Problem market. Share Approach 1: glass box (glass jar …; -): 1 cheapest competitor most expensive competitor 0 price. Per. Item problems: • I have a choice for price. Per. Item • market. Share depends on price. Per. Item 21

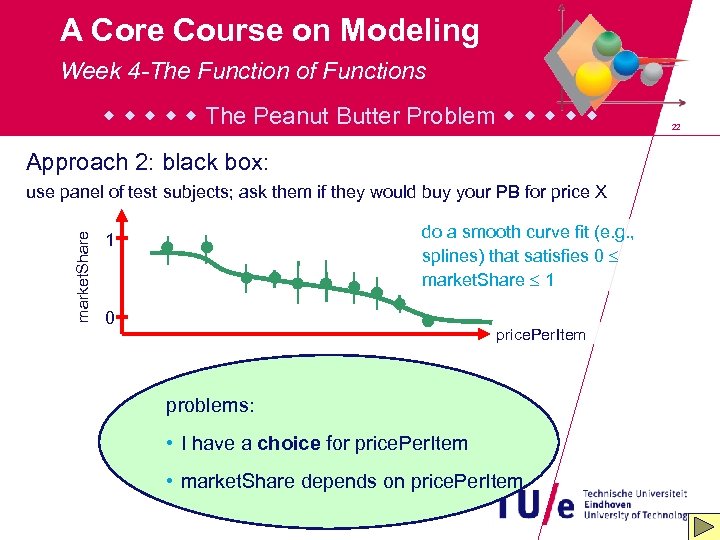A Core Course on Modeling Week 4 -The Function of Functions The Peanut Butter Problem Approach 2: black box: market. Share use panel of test subjects; ask them if they would buy your PB for price X do a smooth curve fit (e. g. , splines) that satisfies 0 market. Share 1 1 0 price. Per. Item problems: • I have a choice for price. Per. Item • market. Share depends on price. Per. Item 22

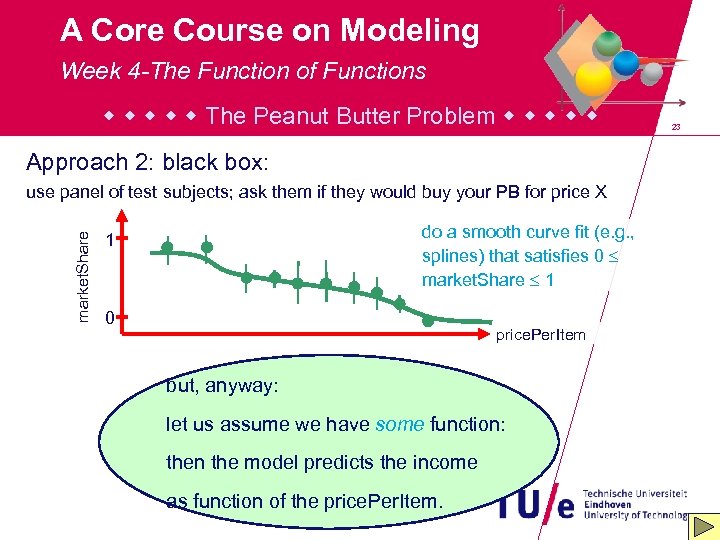A Core Course on Modeling Week 4 -The Function of Functions The Peanut Butter Problem Approach 2: black box: market. Share use panel of test subjects; ask them if they would buy your PB for price X 1 0 do a smooth curve fit (e. g. , splines) that satisfies 0 market. Share 1 price. Per. Item but, anyway: problems: let us assume we have some function: • I have a choice for price. Per. Item then the model predicts the income • market. Share depends on price. Per. Item as function of the price. Per. Item. 23

A Core Course on Modeling Week 4 -The Function of Functions The Peanut Butter Problem Revisit the peanut butter example: income=price. Per. Item * nr. Sold. Items=nr. Sold. Total * market. Share=f(price. Per. Item) for convenience, introduce abbreviations: 24

A Core Course on Modeling Week 4 -The Function of Functions The Peanut Butter Problem This is irrelevant if that the decision to choose MY Realize all customers would equal amounts of Revisit the peanut butter example: buy peanutbutter is taken by a customer. peanutbutter. But: there are mega- of mega Suppose that the majority inc =p. PI * n. SI (inc=income; p. PI=price. Per. Item; n. SI=nr. Sold. Items) consumerscustomers would decide against my and mini-consumers ! n. SI = n. ST * m. Sh 25 peanutbutter – then the (n. ST=nr. Sold. Total; m. Sh=market. Share) original model m. Sh=f(p. PI) So: inc = p. PI * n. ST * m. Sh(p. PI) with m. Sh(p. PI) instead of m. Sh(p. PI, i) would give an overestimate misleading. So: think about which arguments a This is naive: first, realize that n. ST = i n. STi, i ranges over customers. function should depend on! So: inc = p. PI * m. Sh(p. PI) * i n. ST(i) Improved model: inc = p. PI * i n. ST(i) * m. Sh(p. PI, i)

A Core Course on Modeling Week 4 -The Function of Functions The Peanut Butter Problem To go from conceptual model to formal model: while your purpose is not satisfied: • start with quantity you need for the purpose • put this on the to-do list • while the todo list is not empty: • take a quantity from the todo list • think: what does it depend on? • if depends on nothing substitute constant value (perhaps with uncertainty bounds) • else give an expression for it • if possible, use dimensional analysis • propose suitable mathematical expression • think about assumptions • in any case, verify dimensions • add newly introduced quantities to the todo list • todo list is empty: evaluate your model • check if purpose is satisfied; if not, refine your model • ready 26

A Core Course on Modeling Week 4 -The Function of Functions The Peanut Butter Problem To go from conceptual model to formal model: relation wizard while your purpose is not satisfied: 27 function selector e ptot ion asym an ct ar cneed splipurpose • start with quantity you for tilist n the ne • put this on the gis to-do io • while the todo list is not empty: lo from thettodo list nc • take a quantity fu • think: what does it depend on? isa t • if depends on nothing substitute constant value (perhaps with uncertainty bounds) op tim • else give an expression for it • if possible, use dimensional analysis • propose suitable mathematical expression • think about assumptions • in any case, verify dimensions • add newly introduced quantities to the todo list • todo list is empty: evaluate your model • check if purpose is satisfied; if not, refine your model • ready

A Core Course on Modeling Week 4 -The Function of Functions Summary 28 • Conceptual model formal model : not in a formally provable correct way; • Appropriate naming • Structure • Chain of dependencies: the formal model as a directed acyclic graph; • What mechanism? • What quantities drive this mechanism? • What is the qualitative behavior of the mechanism? • What is the mathematical expression to describe this mechanism? • To-do-list : all intermediate quantities are found and elaborated in turn; • Formation of mathematical expressions: • dimensional analysis mathematical expressions, e. g in the case of proportionality • the Relation Wizard can help finding appropriate fragments of mathematics; • the Function Selector can help finding an appropriate expression for a desired behavior; • wisdom of the crowds can help improve the accuracy of guessed values;