1facd9a1c958310e038522409f2b7ca6.ppt
- Количество слайдов: 46

A Brief History of Cryptography Sandy Kutin CSPP 532 University of Chicago

What is cryptography? • “hidden writing” • Until recently: military tool • Like any military technology: methods change over time • Two sides: designing codes breaking codes (cryptanalysis) • Computers have changed both
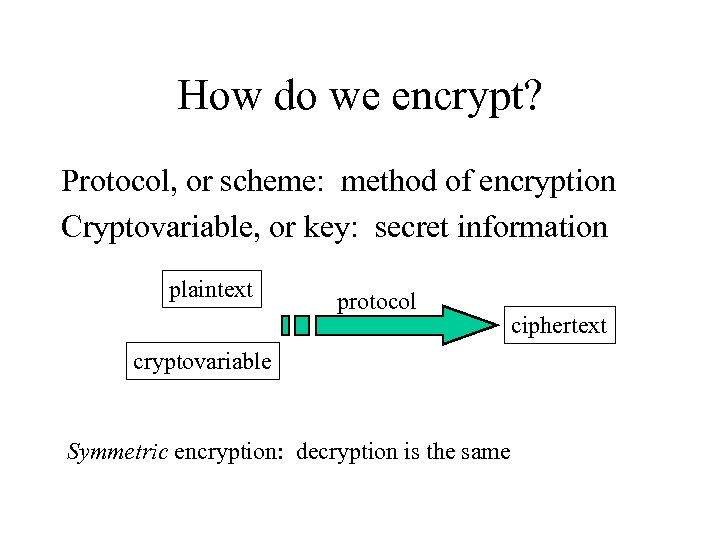
How do we encrypt? Protocol, or scheme: method of encryption Cryptovariable, or key: secret information plaintext protocol cryptovariable Symmetric encryption: decryption is the same ciphertext

Example: Caesar Shift • Protocol: shift each letter by the same amount • Cryptovariable: amount to shift IBM HAL -1 Veni, vidi, vici Foxs, fsns, fsms 10 • Decryption: shift back the same amount

How could we break this? • Case I: we don’t know the protocol – Hard problem in cryptanalysis – “Clark Kent” effect • Case II: we know the protocol – Need to guess the cryptovariable – Only 26 possibilities

auffcuxcpcmuymnchnlymjulnym bvggdvydqdnvznodiomznkvmozn cwhhewzereowaopejpnaolwnpao dxiifxafsfpxbpqfkqobpmxoqbp eyjjgybgtgqycqrglrpcqnyprcq fzkkhzchuhrzdrshmsqdrozqsdr galliadivisaestintrespartes Decrypt key = 6 Encrypt key = 20

Substitution Cipher • • Allow any permutation of the alphabet Key = permutation; 26! possibilities 26! = 403, 291, 461, 126, 605, 635, 584, 000 Roughly 288: checking 1 billion per second, would take 12 billion years • Is there a better way? • al-Kindi, ninth century: frequency analysis

H EKGGLHQNL KZEL AKGB PL ARHA ARL CKSGB CHV XNGG KX UHB VLENSTAF VFVALPV CSTAALZ UF OLKOGL CRK SLHB HOOGTLB ESFOAKQSHORF. - USNEL VERZLTLS, VLESLAV HZB GTLV L occurs 18 times, A occurs 10 times.

E E ET ET T H EKGGLHQNL KZEL AKGB PL ARHA TE ARL CKSGB CHV XNGG KX UHB E T TE TTE VLENSTAF VFVALPV CSTAALZ UF E E OLKOGL CRK SLHB HOOGTLB T ESFOAKQSHORF. E E ET E - USNEL VERZLTLS, VLESLAV HZB GTLV

E E E TH T H EKGGLHQNL KZEL AKGB PL ARHA THE ARL CKSGB CHV XNGG KX UHB E T TE TTE VLENSTAF VFVALPV CSTAALZ UF E E H E E OLKOGL CRK SLHB HOOGTLB T H ESFOAKQSHORF. E H E ET E - USNEL VERZLTLS, VLESLAV HZB GTLV

A EA E E THAT H EKGGLHQNL KZEL AKGB PL ARHA THE A A ARL CKSGB CHV XNGG KX UHB E T TE TTE VLENSTAF VFVALPV CSTAALZ UF E E H EA A E OLKOGL CRK SLHB HOOGTLB T AH ESFOAKQSHORF. E H E ET A E - USNEL VERZLTLS, VLESLAV HZB GTLV

A OLLEA E O E TOL E THAT H EKGGLHQNL KZEL AKGB PL ARHA THE O L A LL O A ARL CKSGB CHV XNGG KX UHB SE T S STE S TTE VLENSTAF VFVALPV CSTAALZ UF PEOPLE HO EA APPL E OLKOGL CRK SLHB HOOGTLB PTO APH ESFOAKQSHORF. E S H E E SE ETS A L ES - USNEL VERZLTLS, VLESLAV HZB GTLV

A COLLEAGUE ONCE TOLD ME THAT H EKGGLHQNL KZEL AKGB PL ARHA THE WORLD WAS FULL OF BAD ARL CKSGB CHV XNGG KX UHB SECURITY SYSTEMS WRITTEN BY VLENSTAF VFVALPV CSTAALZ UF PEOPLE WHO READ APPLIED OLKOGL CRK SLHB HOOGTLB CRYPTOGRAPHY. ESFOAKQSHORF. BRUCE SCHNEIER, SECRETS AND LIES - USNEL VERZLTLS, VLESLAV HZB GTLV

A harder example YIRLAZ MRACIRB CR PKORI CRP: MRPPVAMQAY MRLACZRGA, VAYQAVW RA • Shorter = less information • R occurs 10 times, A occurs 9 times – (all others occur 4 or fewer times) • Telegraph style; fewer short words

A harder example E E E YIRLAZ MRACIRB CR PKORI CRP: E E MRPPVAMQAY MRLACZRGA, VAYQAVW RA E doesn’t begin any common 2 -letter words

A harder example O O O YIRLAZ MRACIRB CR PKORI CRP: O O MRPPVAMQAY MRLACZRGA, VAYQAVW RA A occurs 9 times. What could it be?

A harder example O N ON O O YIRLAZ MRACIRB CR PKORI CRP: O N N N ON MRPPVAMQAY MRLACZRGA, VAYQAVW RA

A harder example O N ONT O TO YIRLAZ MRACIRB CR PKORI CRP: O N N O NT O N N N ON MRPPVAMQAY MRLACZRGA, VAYQAVW RA

A harder example G O N ONT O TO YIRLAZ MRACIRB CR PKORI CRP: O N ING O NT O N NGIN ON MRPPVAMQAY MRLACZRGA, VAYQAVW RA

A harder example GROUND CONTROL TO MAJOR TOM: YIRLAZ MRACIRB CR PKORI CRP: COMMENCING COUNTDOWN, ENGINES ON MRPPVAMQAY MRLACZRGA, VAYQAVW RA

What have we learned? • • • A large space of keys is not enough Some of the key never got used (Q, Z, X) We were able to guess a little bit at a time Features of the plaintext can show through The more plaintext we have, the easier it is to decode • Don’t use the same key too often

The perfect cryptosystem • One-time pad: encrypt each letter with its own key • Example: Caesar shift each letter separately • Ci = Pi + Ki (mod 26) • To encrypt n bits, use n bits of key • This uses up lots of key bits; need to prearrange • How do you generate key bits?

Vigenère Cipher • • • Blaise de Vigenère (c. 1562) Ci = Pi + Ki (mod 26) Key repeats with a short cycle Frequency analysis doesn’t work Caught on with the telegraph, considered “unbreakable” • Broken by Babbage, Kasiski (c. 1860)

Enigma Machine • • German cryptosystem in World War II Same idea: modify letters Scrambler disks implement permutation Rotate after each letter, so many different permutations used • Additional permutation provided by plugboard
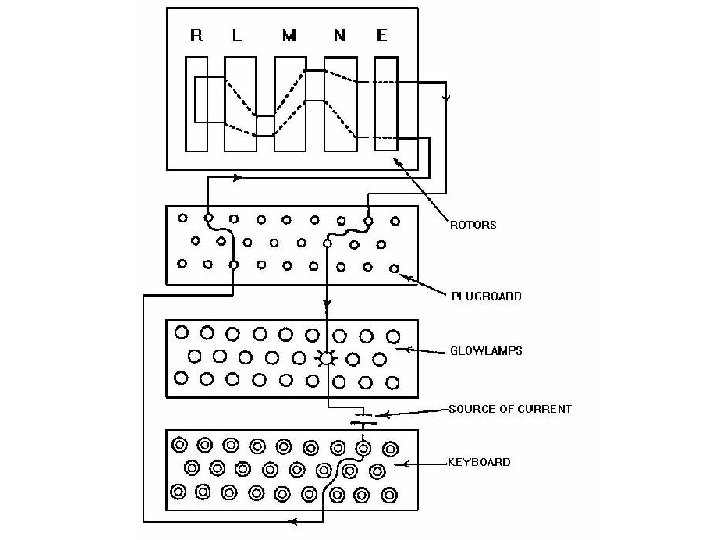


Enigma Key • Key changed daily • 3 scramblers in one of 6 orders – In 1938: 3 of 5, so 60 arrangements • • • 263 = 17, 576 settings for scramblers Billions of plugboard settings Alan Turing: bypassed plugboard Used known plaintext, exhausted over space British were able to read traffic

Navajo Code Talkers • Americans in the Pacific during WWII • Each troop had one Navajo • Even after figuring out system, Japanese couldn’t break it • Like a one-time pad: prearranged secret is a whole language • May not be feasible today

Modern Symmetric Cryptography • • Assume the protocol is known to the enemy Only the key is secret Encryption, cryptanalysis use computers Operate on bits, rather than letters DES, AES Open standards; let everyone try to break it Closed design often fails (cell phones) Don’t try this in-house

Intermission

Key Distribution • Secure communication requires a key • How do you exchange keys securely? • Military: codebooks in field could fall into enemy hands • Commerce: might not meet face-to-face • Seems to be a Catch-22

Paradigm Shift • • Alice wants to mail Bob a letter securely If they share a “key”, Alice locks, Bob unlocks If not: Alice puts on padlock, sends box to Bob adds his padlock, sends box back to Alice removes her padlock, sends box to Bob unlocks box, reads letter Problem: how to translate this to mathematics
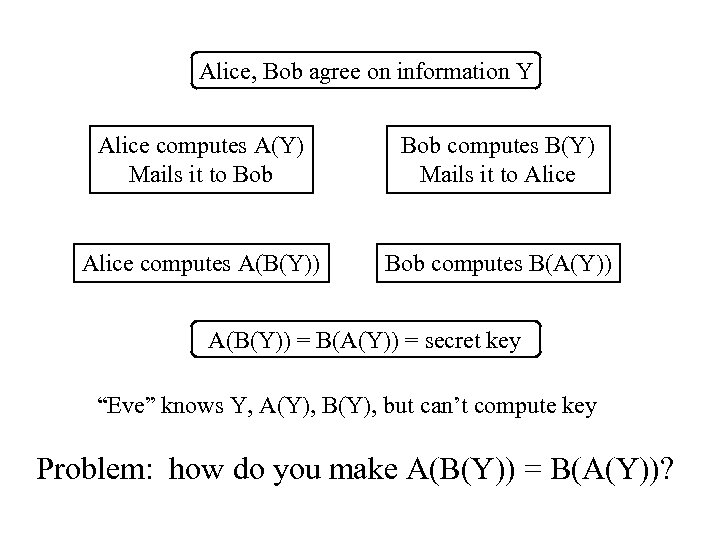
Alice, Bob agree on information Y Alice computes A(Y) Mails it to Bob computes B(Y) Mails it to Alice computes A(B(Y)) Bob computes B(A(Y)) A(B(Y)) = B(A(Y)) = secret key “Eve” knows Y, A(Y), B(Y), but can’t compute key Problem: how do you make A(B(Y)) = B(A(Y))?

Diffie-Hellman-Merkle (1976) • • Modular Arithmetic Choose Y, modulus p Alice’s function is YA (mod p) Bob’s function is YB (mod p) Key is YAB YBA (mod p) Eve can’t compute YAB from Y, YA, YB We think (no one can prove it) One problem: must communicate to get key

One-way Functions • • • Easy to compute, hard to reverse Example: f (A) = YA (mod p) f -1(YA) is called “discrete log” Hard to compute (we think) Could always do exhaustive search Here, there are p-1 choices

Cryptographic Primitives • Building blocks for algorithms – Example: one-way functions • Protocols built out of primitives – Example: Diffie-Hellman-Merkle • Protocols built out of other protocols – Example: • 1. Use Diffie-Hellman to exchange key • 2. Use symmetric encryption, key to encode message • Good, “modular” design

Trapdoor one-way functions • • Another useful primitive f (X) is easy to compute f -1(Y) is hard for most people to compute But: easy to compute if you know a secret There are trapdoor one-way functions Found by Rivest-Shamir-Adleman, 1977 Rely on difficulty of factoring large integers

Idea behind public key • • Bob publishes design specs for a padlock Alice wants to send Bob a box Alice builds a Bob padlock, locks the box Bob unlocks box using his key Eve intercepts box, knows design specs Goal: Eve still can’t build a key Padlock = trapdoor one-way function

Public Key Cryptography • • Alice wants to talk to Bob: computes key X Alice sends Bob f. B (X) (Bob’s function) Bob computes f. B-1 (f. B (X)) = X Both Alice and Bob know X, use as key for symmetric encryption • Eve knows f. B (X); can’t compute X • Asymmetric encryption • Whitfield Diffie, 1975

Digital Signature Scheme • • • Alice wants to send Bob a message, sign it Alice sends Bob X and S = f. A-1 (X) Bob checks that f. A (S) = X Therefore Bob knows that S = f. A-1 (X) Only Alice can compute f. A-1 (X) easily, so Alice must have sent the message • Same primitive, new protocol

Revolution • New ideas made cryptography an option for commerce • PCs gave everyone computing power • Zimmerman’s PGP: gave everyone access • SSL in web browsers • I use ssh every day

A COLLEAGUE ONCE TOLD ME THAT H EKGGLHQNL KZEL AKGB PL ARHA THE WORLD WAS FULL OF BAD ARL CKSGB CHV XNGG KX UHB SECURITY SYSTEMS WRITTEN BY VLENSTAF VFVALPV CSTAALZ UF PEOPLE WHO READ APPLIED OLKOGL CRK SLHB HOOGTLB CRYPTOGRAPHY. ESFOAKQSHORF. BRUCE SCHNEIER, SECRETS AND LIES - USNEL VERZLTLS, VLESLAV HZB GTLV

You are the weakest link • Cryptographic system only as strong as the weakest link – Example • 1. Use RSA to exchange a key • 2. Use key to generate permutation of 26 letters • 3. Encrypt message with substitution cipher • Schneier: defend castle with 100 -foot pole • Often, users are the weakest link

Quantum Computation • Computers revolutionized cryptographic design and cryptanalysis • Quantum computers may one day do the same • Quantum key exchange: guaranteed secure • A quantum computer could factor large integers in polynomial time • We may never live to see one

Where do we go from here? • Math necessary to understand RSA, DES • Protocols using mathematics • Implementation issues: – Software (bugs, patches) – Hardware (tamper-resistant mechanisms) – Wetware (social engineering) • Politics (who makes cryptographic decisions) • Religion (Microsoft)

Recommended Reading Stallings, Chapter 2
1facd9a1c958310e038522409f2b7ca6.ppt