e801e780672f2d9f1025ddf7cc31ee7f.ppt
- Количество слайдов: 47

A Bonus Presentation on Location

A problem in location Customers per day/7 -day week Big Burger, a fast food chain, has 20 stores in the Southwest Ohio area located at the following coordinates where the units are in miles. Big Burger is considering constructing a receiving and distribution center for this region. Where to locate the distribution center has preoccupied top management for some time. On the average, a delivery truck must stop at each Big Burger every 1000 customers.

Solve the following problems: Criteria: Minimize The weighted squared distance Sum of the Euclidean distances Weighted sum of the Euclidean distances Maximum Euclidean distance Sum of rectilinear distances Weighted sum of the rectilinear distances Maximum rectilinear distance A Big Burger chef
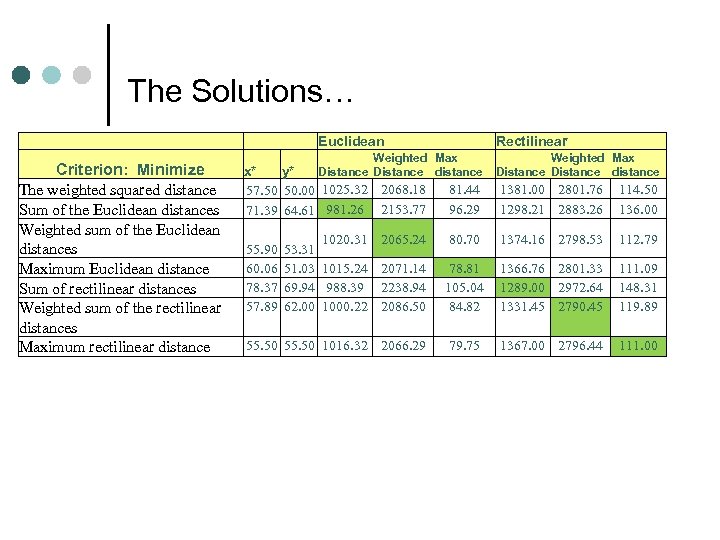
The Solutions… Euclidean Rectilinear Criterion: Minimize The weighted squared distance Sum of the Euclidean distances Weighted sum of the Euclidean distances Maximum Euclidean distance Sum of rectilinear distances Weighted sum of the rectilinear distances Maximum rectilinear distance x* y* Distance distance 81. 44 1381. 00 2801. 76 114. 50 57. 50 50. 00 1025. 32 2068. 18 96. 29 1298. 21 2883. 26 136. 00 71. 39 64. 61 981. 26 2153. 77 Weighted Max 1020. 31 2065. 24 53. 31 51. 03 1015. 24 2071. 14 69. 94 988. 39 2238. 94 62. 00 1000. 22 2086. 50 80. 70 1374. 16 2798. 53 112. 79 78. 81 105. 04 84. 82 1366. 76 2801. 33 1289. 00 2972. 64 1331. 45 2790. 45 111. 09 148. 31 119. 89 55. 50 1016. 32 2066. 29 79. 75 1367. 00 2796. 44 111. 00 55. 90 60. 06 78. 37 57. 89
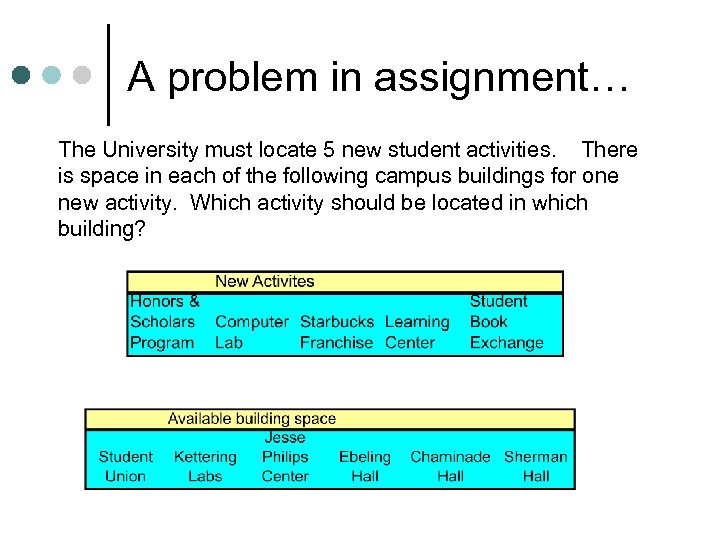
A problem in assignment… The University must locate 5 new student activities. There is space in each of the following campus buildings for one new activity. Which activity should be located in which building?
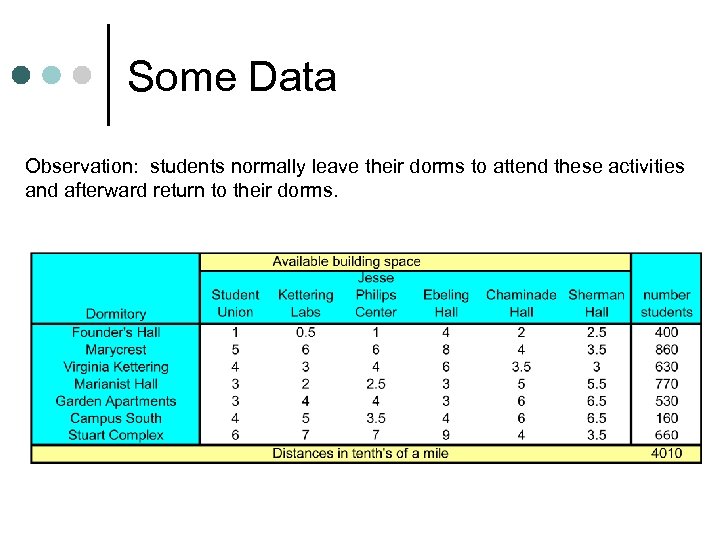
Some Data Observation: students normally leave their dorms to attend these activities and afterward return to their dorms.
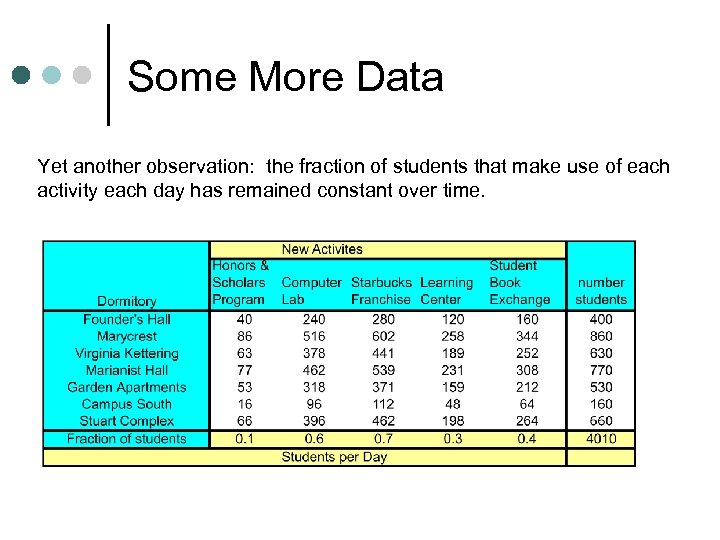
Some More Data Yet another observation: the fraction of students that make use of each activity each day has remained constant over time.

Let’s do some matrix multiplication… At B = Student tenth’s of a mile per day Let Solver do the work…
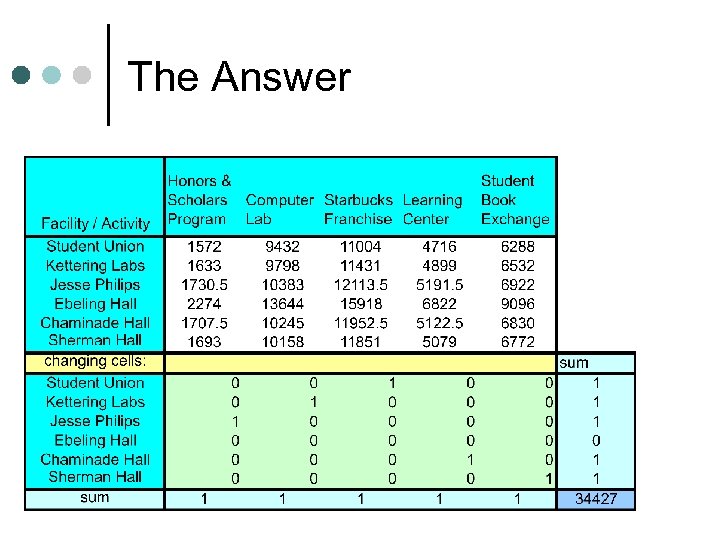
The Answer

A problem in campus layout ¢ The University of Dayton, in its continuing efforts to make academic life as good as possible for the students, has decided to relocate its schools and departments and their respective classrooms. The objective is to minimize the total distances the students have to walk to get to their next class. By reducing travel time to the next class, classes can be extended from 50 to 55 minutes thus increasing by 10 percent the amount of learning that takes place.
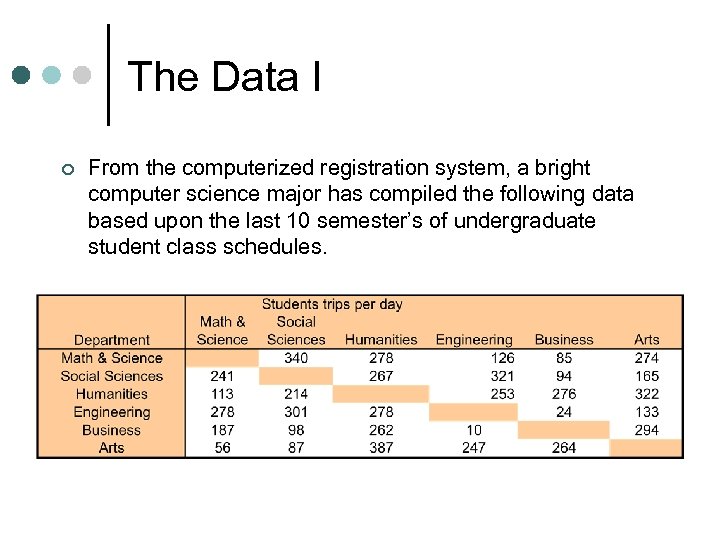
The Data I ¢ From the computerized registration system, a bright computer science major has compiled the following data based upon the last 10 semester’s of undergraduate student class schedules.
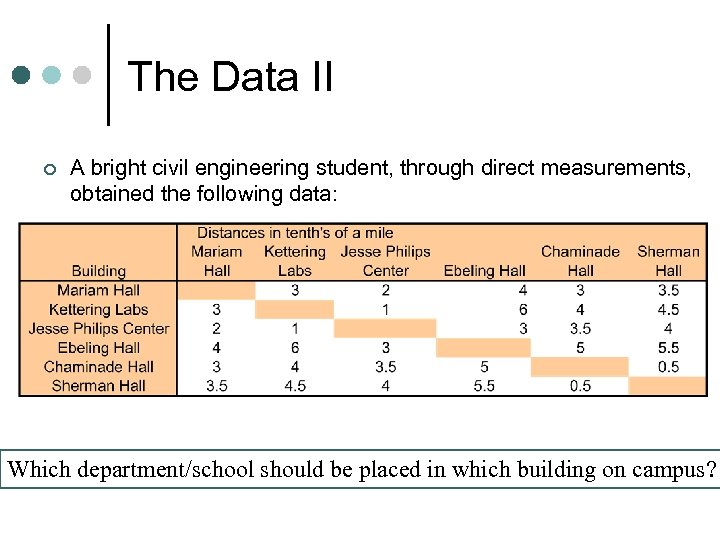
The Data II ¢ A bright civil engineering student, through direct measurements, obtained the following data: Which department/school should be placed in which building on campus?

Discrete Location - A Meeting Place ¢ ¢ ¢ The Traveler Corporation has its home office in New York and branch offices 15 other cities. The Company has monthly sales conferences in one of these cities in which the entire sales force is brought together. Currently, each branch office has taken turns in hosting these meetings. However, the expense of these meetings has raised concern with top management. The problem is to determine which city should be hosting these conferences in order to minimize the total travel expense to the company.

The Expenses ¢ ¢ ¢ The primary expenses are the travel fares and the per diem that consists of an allowance for meals, lodging, and other incidental expenses (ML&IE). (GSA rates apply) Unless the sales representative lives within 200 miles of the hosting city, the individual will fly at the cheapest commercial rate available. l If they live within 200 miles, then it is assumed that the individual drives and is reimbursed at the rate of 34 cents a mile. l Flyers are assumed to take ¾ a day to reach their destination and ¾ a day to return in which case they receive a corresponding partial per diem. l For per diem purposes, drivers are allowed ½ a day each for travel to and from the conference. Conferences normally last 4 days at the full per diem. Individuals living in the host city receive no travel compensation.
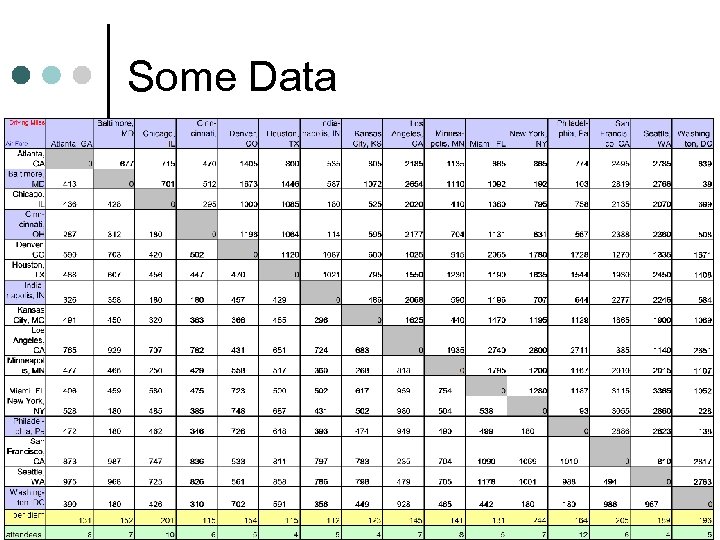
Some Data

The Alternatives Evaluated

Global Airlines operates a major hub for their North American operations in Hazard (pop 5400), Kentucky. They operate out of Terminal 2 that has 11 gates equally distant apart in a linear configuration as shown below. TERMINAL BUILDING 2 G 1 G 2 G 3 G 4 G 5 G 6 G 7 G 8 G 9 G 10 G 11 Each morning and each afternoon, there are 11 flights arriving at the terminal. Data has been obtained on the average number of passengers arriving on the morning flights that transfer between each pair of flights[1]. [1] This data was obtained from an extensive database containing over a years worth of passenger flight data using data mining techniques.
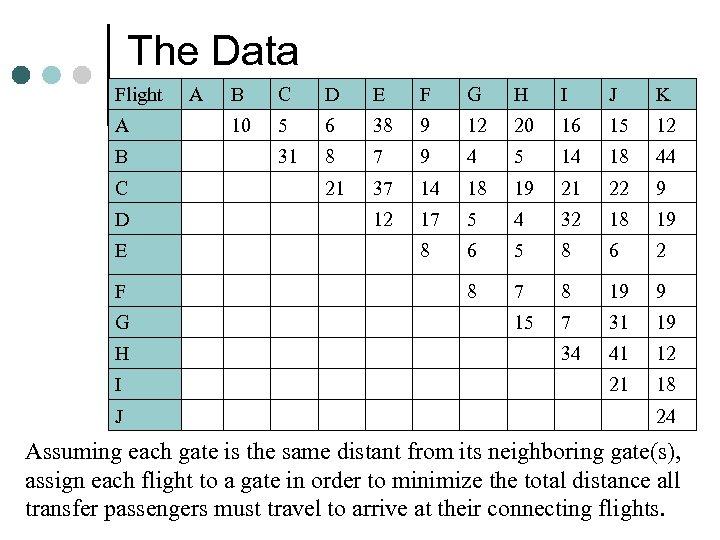
The Data Flight A B C D E F G H I J K 10 5 6 38 9 12 20 16 15 12 31 8 7 9 4 5 14 18 44 21 37 14 18 19 21 22 9 12 17 5 4 32 18 19 8 6 5 8 6 2 8 7 8 19 9 15 7 31 19 34 41 12 21 18 24 Assuming each gate is the same distant from its neighboring gate(s), assign each flight to a gate in order to minimize the total distance all transfer passengers must travel to arrive at their connecting flights.
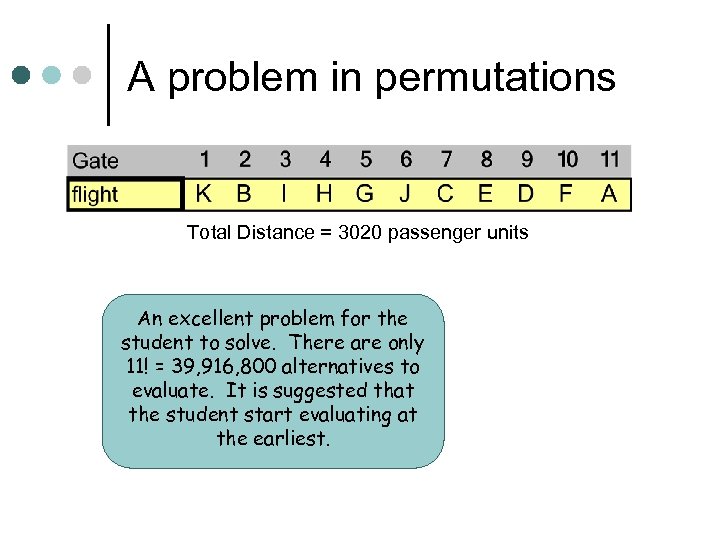
A problem in permutations Total Distance = 3020 passenger units An excellent problem for the student to solve. There are only 11! = 39, 916, 800 alternatives to evaluate. It is suggested that the student start evaluating at the earliest.

Global Airlines Revisited ¢ ¢ ¢ Global Air operates a major hub at its Kentucky facility. An objective of Global Air is to allow as many passengers that are transferring to another flight to remain on the same aircraft. This minimizes baggage handling and passenger boarding while maximizing passenger convenience. l l ¢ Thru-flight connections must involve flights requiring the same aircraft type and have sufficient arrival and departure times to complete servicing. A minimum of 30 minutes is required between the arrival of an aircraft and its departure. Determine which arrival and departure flights should share the same aircraft.

The Data Fllights GB 247 GB 561 GB 120 GB 404 GB 782 GB 123 GB 201 GB 220 GB 310 GB 321 GB 300 GB 341 GB 353 GB 360 GB 372 GB 380 dep time GB 40 GB 50 GB 20 GB 483 GB 76 GB 123 GB 10 GB 12 GB 852 GB 743 GB 58 GB 54 GB 53 GB 12 arrival 47 2 2 1 1 26 7 0 14 54 1 time 5. 4 32. 4 7. 2 18 0 27 12. 6 7. 2 1: 45 PM 5. 7 0 5. 7 6. 84 7. 98 2. 28 10. 26 12. 54 13. 68 8. 55 7. 41 5. 7 17. 1 10. 26 9: 30 AM 24. 8 7. 44 12. 4 17. 36 0 0 34. 72 52. 08 0 42. 16 44. 64 0 12. 4 0 7: 45 AM 30. 2 0 0 0 70 5. 25 43. 75 0 0 35 12. 25 10: 00 AM 20. 1 0 999 18. 09 0 30. 15 24. 12 14. 07 1: 15 PM 14. 64 9. 15 16. 47 1. 83 3. 66 0 0 18. 3 27. 45 32. 94 27. 45 21. 96 0 9. 15 10: 00 AM 11 0 13. 2 0 9. 9 6. 6 0 0 24. 2 12. 1 5. 5 0 11 16. 5 8: 30 PM 8. 13 13. 55 27. 1 0 27. 1 21. 68 27. 1 0 10. 84 46. 07 43. 36 18. 97 8. 13 9: 40 PM 29. 7 0 4. 95 0 0 8. 25 0 16. 5 24. 75 4. 95 21. 45 24. 75 0 29. 7 8: 50 AM 0 6. 15 2. 46 12. 3 11. 07 14. 76 24. 6 0 27. 06 0 12. 3 2. 46 3. 69 8: 40 AM 25. 6 19. 2 22. 4 0 0 3. 2 0 32 67. 2 54. 4 80 0 16 9: 20 AM 7. 12 12. 46 0 0 16. 02 3. 56 16. 02 35. 6 53. 4 10. 68 12. 46 3. 56 7: 35 AM 10. 15 4. 06 7 16. 24 5. 4 12. 18 0 0 56. 84 0 0 10: 00 AM 0 19. 2 0 0 0 30. 72 0 0 17. 28 0 20. 16 8. 64 0 0 8: 00 AM 5. 4 11. 1 15. 1 15. 84 0 0 10. 08 3. 84 3. 36 2. 4 1. 92 10: 45 PM 16. 38 7. 28 54. 6 3. 64 9. 1 61. 88 5. 46 3. 64 1. 82 3. 64 5. 46 7: 50 PM 3: 29 PM 2: 19 PM 1: 42 PM 10: 20 AM 3: 11 PM 10: 14 AM 2: 38 PM 5: 21 PM 11: 24 AM 12: 57 PM 2: 00 PM 4: 30 PM 2: 51 PM 9: 55 AM The (historical) mean number of passengers that arrive on a particular flight and transfer to another departing flight.

The Factory Floor ¢ ¢ ¢ The Makeit Company assembles nine different products in the same plant. Each product is assembled from 13 different types of raw material and vendor supplied parts that are shipped to the company and stored within the plant. There are 11 potential sites on the factory floor available for the assembly of each product. A significant non-value added production cost is the material handling requirements for moving the raw material to the assembly sites. All movement on the factory floor is by necessity rectilinear. The problem is to determine which products should be assembled at which sites in order to minimize the total number of forklift feet required to support a single production shift.
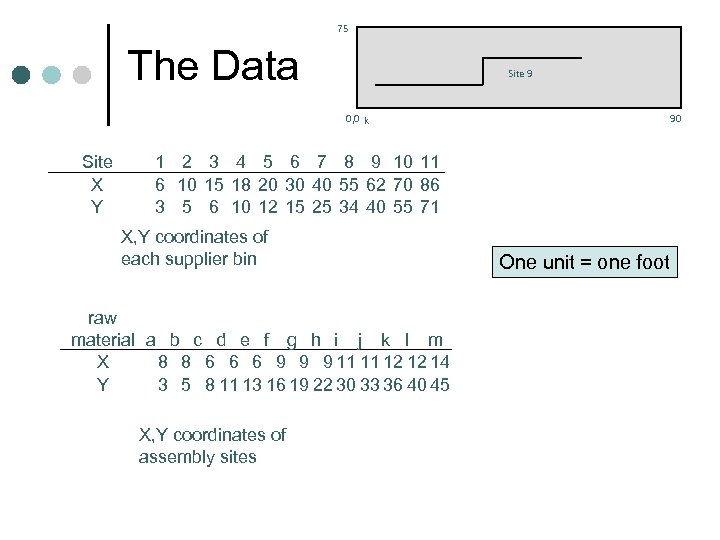
75 The Data Site 9 90 0, 0 k Site X Y 1 2 3 4 5 6 7 8 9 10 11 6 10 15 18 20 30 40 55 62 70 86 3 5 6 10 12 15 25 34 40 55 71 X, Y coordinates of each supplier bin raw material a b c d e f g h i j k l m X 8 8 6 6 6 9 9 9 11 11 12 12 14 Y 3 5 8 11 13 16 19 22 30 33 36 40 45 X, Y coordinates of assembly sites One unit = one foot
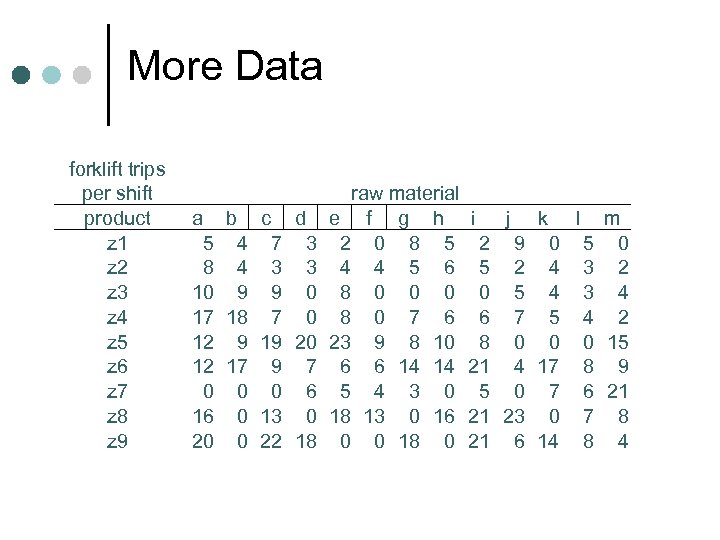
More Data forklift trips per shift product a b z 1 5 4 z 2 8 4 z 3 10 9 z 4 17 18 z 5 12 9 z 6 12 17 z 7 0 0 z 8 16 0 z 9 20 0 c 7 3 9 7 19 9 0 13 22 d 3 3 0 0 20 7 6 0 18 raw material e f g h i j k l m 2 0 8 5 2 9 0 5 0 4 4 5 6 5 2 4 3 2 8 0 0 5 4 3 4 8 0 7 6 6 7 5 4 2 23 9 8 10 8 0 0 0 15 6 6 14 14 21 4 17 8 9 5 4 3 0 5 0 7 6 21 18 13 0 16 21 23 0 7 8 0 0 18 0 21 6 14 8 4
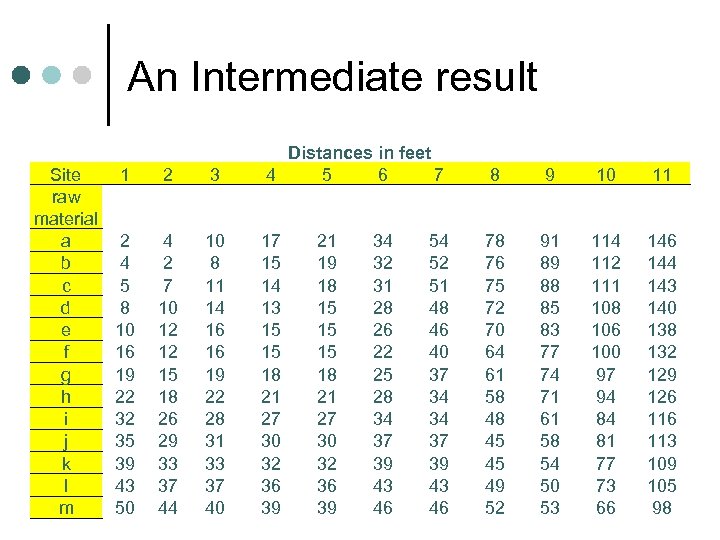
An Intermediate result Site raw material a b c d e f g h i j k l m 1 2 3 Distances in feet 4 5 6 7 2 4 5 8 10 16 19 22 32 35 39 43 50 4 2 7 10 12 12 15 18 26 29 33 37 44 10 8 11 14 16 16 19 22 28 31 33 37 40 17 15 14 13 15 15 18 21 27 30 32 36 39 21 19 18 15 15 15 18 21 27 30 32 36 39 34 32 31 28 26 22 25 28 34 37 39 43 46 54 52 51 48 46 40 37 34 34 37 39 43 46 8 9 10 11 78 76 75 72 70 64 61 58 48 45 45 49 52 91 89 88 85 83 77 74 71 61 58 54 50 53 114 112 111 108 106 100 97 94 84 81 77 73 66 144 143 140 138 132 129 126 113 109 105 98

More Intermediate results product Site 1 2 3 4 5 6 7 8 9 10 11 z 1 961 839 1015 1065 1135 1607 2153 3099 3689 4839 6439 z 2 1017 889 1067 1122 1188 1683 2291 3319 3932 5131 6827 z 3 z 4 z 5 z 6 841 1390 2067 3192 781 1222 1951 2736 957 1562 2389 3148 1093 1783 2500 3272 1205 1951 2700 3438 1769 2844 4083 4740 2489 3964 6061 6120 3459 5682 8903 8690 4035 6721 10452 10290 5191 8702 13361 13512 6855 11486 17617 18120 z 7 z 8 z 9 1960 3015 2608 1720 2639 2338 1718 3031 2728 1661 3076 2845 1673 3192 3049 2128 4383 4326 2456 5653 5742 3162 8045 8112 3551 9620 9615 4652 12645 12588 6476 16965 16780 Feet per shift = distance in feet x trips per shift
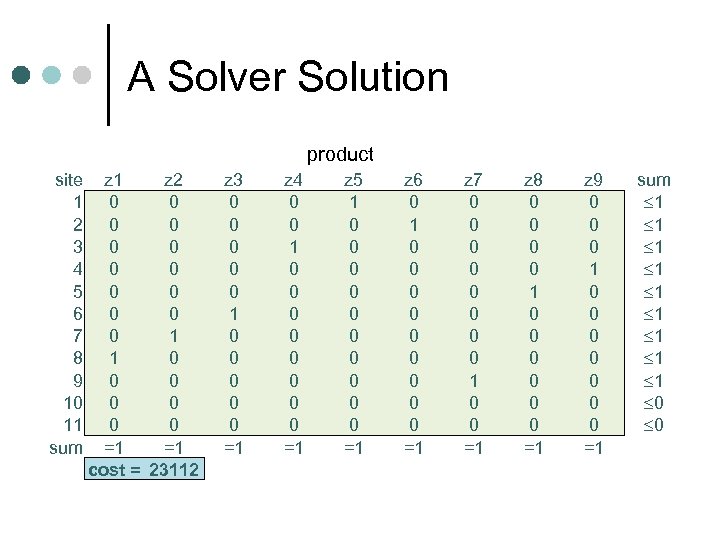
A Solver Solution product site 1 2 3 4 5 6 7 8 9 10 11 sum z 1 z 2 0 0 0 0 1 1 0 0 0 0 =1 =1 cost = 23112 z 3 0 0 0 1 0 0 0 =1 z 4 0 0 1 0 0 0 0 =1 z 5 1 0 0 0 0 0 =1 z 6 0 1 0 0 0 0 0 =1 z 7 0 0 0 0 1 0 0 =1 z 8 0 0 1 0 0 0 =1 z 9 0 0 0 1 0 0 0 0 =1 sum 1 1 1 1 1 0 0
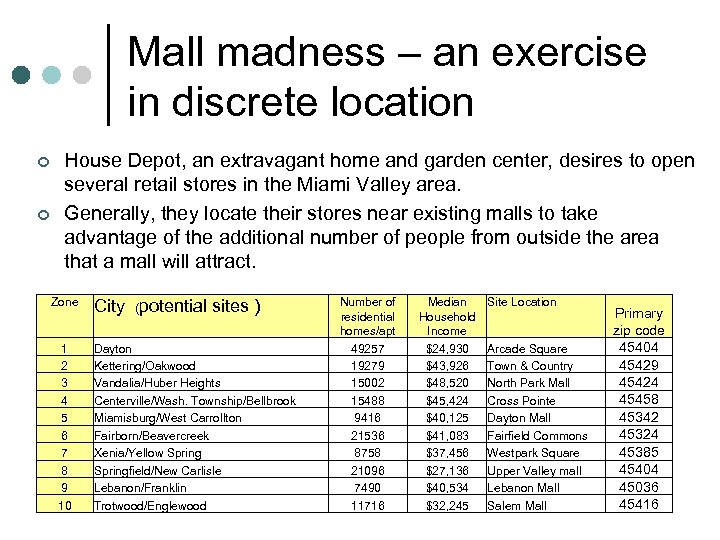
Mall madness – an exercise in discrete location ¢ ¢ House Depot, an extravagant home and garden center, desires to open several retail stores in the Miami Valley area. Generally, they locate their stores near existing malls to take advantage of the additional number of people from outside the area that a mall will attract. Zone 1 2 3 4 5 6 7 8 9 10 City (potential sites ) Dayton Kettering/Oakwood Vandalia/Huber Heights Centerville/Wash. Township/Bellbrook Miamisburg/West Carrollton Fairborn/Beavercreek Xenia/Yellow Springfield/New Carlisle Lebanon/Franklin Trotwood/Englewood Number of residential homes/apt 49257 19279 15002 15488 9416 21536 8758 21096 7490 11716 Median Household Income $24, 930 $43, 926 $48, 520 $45, 424 $40, 125 $41, 083 $37, 456 $27, 136 $40, 534 $32, 245 Site Location Arcade Square Town & Country North Park Mall Cross Pointe Dayton Mall Fairfield Commons Westpark Square Upper Valley mall Lebanon Mall Salem Mall Primary zip code 45404 45429 45424 45458 45342 45324 45385 45404 45036 45416

Mall madness ¢ House Depot is a firm believer in the following retail-gravity model: where Sij = annual sales in zone j made by residents of zone i Pi = number of residential homes in zone i ei = median household income cij = cost of travel from zone i to zone j (usually proportional to the distance) Wj = size (attractiveness) of the House Depot in zone j, measured in square feet K = constant of proportionality determined empirically and found to be equal to 0. 000000011 (1. 1 x 10 -8).

The Model ¢ ¢ The gravity model is based upon several “reasonable” assumptions that include: (1) The flow of cash from zone i to j is proportional to the total amount of cash available for shopping in zone i; (2) The flow of cash from i to j is proportional to the “attractiveness” (i. e. size) of the store in zone j; and (3) The flow of cash from i to j is inversely proportional to the travel cost. Reference: Wilson, A. G. , Urban and Regional Models in Geography and Planning, Wiley, New York, 1974.

Data Collection begins… Road Distances in miles zone 1 2 3 4 5 6 7 8 9 10 1 4 8. 5 5 17. 5 14. 9 8. 2 16. 7 29. 6 31. 8 10. 7 2 8. 5 3 13 5. 2 13. 4 15. 8 17. 5 32. 5 17. 5 13. 7 3 5 13 5 23. 3 18. 8 10. 8 21. 2 18. 5 36. 8 15. 7 4 17. 5 5. 2 23. 3 5 13 18. 3 20 35 12. 4 22. 7 5 14. 9 13. 4 18. 8 13 5 21. 3 26. 5 38. 7 19. 1 16. 2 6 8. 2 15. 8 10. 8 18. 3 21. 3 4. 5 17. 3 15. 9 30. 6 15. 5 7 16. 7 17. 5 21. 2 20 26. 5 17. 3 6 20. 5 23. 9 8 29. 6 32. 5 18. 5 35 38. 7 15. 9 20. 5 5. 5 47. 3 33. 5 9 31. 8 17. 5 36. 8 12. 4 19. 1 30. 6 23. 9 47. 3 3 35. 9 10 10. 7 13. 7 15. 7 22. 7 16. 2 15. 5 23. 9 33. 5 35. 9 3

Other considerations ¢ ¢ ¢ Travel cost is estimated to be $. 40 per mile. Construction of a new store will incur a fixed cost (primary the cost of the land) and a variable cost per square foot. For the Miami Valley region, the company has allocated a construction budget of $5, 000 and a total floor space capacity of 80, 000 square feet. By company policy, no more than 5 stores can be located in the same region and no two stores can be within ten miles of one another. The problem: From the data, determine at which locations House Depot should open stores in the Miami Valley region and determine the size in square feet of each store in order to maximize total annual sales.
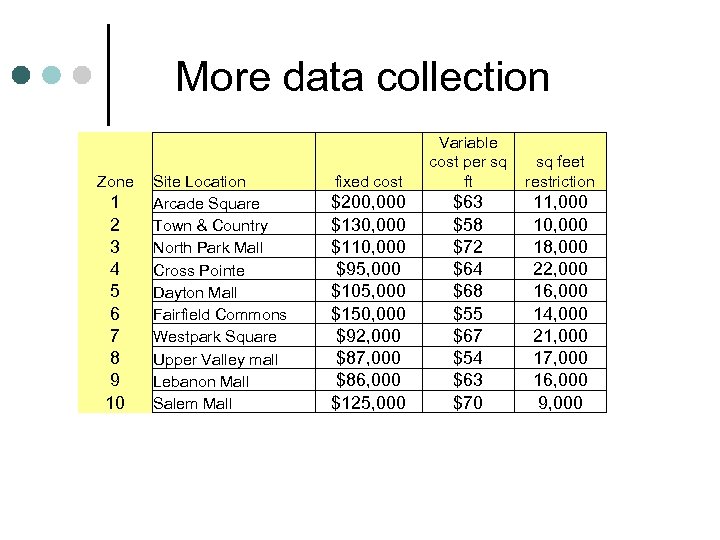
More data collection Zone 1 2 3 4 5 6 7 8 9 10 Site Location Arcade Square Town & Country North Park Mall Cross Pointe Dayton Mall Fairfield Commons Westpark Square Upper Valley mall Lebanon Mall Salem Mall fixed cost $200, 000 $130, 000 $110, 000 $95, 000 $105, 000 $150, 000 $92, 000 $87, 000 $86, 000 $125, 000 Variable cost per sq sq feet ft restriction $63 $58 $72 $64 $68 $55 $67 $54 $63 $70 11, 000 10, 000 18, 000 22, 000 16, 000 14, 000 21, 000 17, 000 16, 000 9, 000

The Model W 1 = floor space of store in zone i Yi = binary, 1 if store in zone i; 0 otherwise MAX 22. 26115 W 1+21. 54661 W 2+18. 34966 W 3+15. 29732 W 4+11. 60323 W 5+16. 85215 W 6 +10. 11839 W 7+9. 079918 W 8+9. 618649 W 9+13. 73721 W 10 SUBJECT TO W 1+W 2+W 3+W 4+W 5+W 6+W 7+W 8+W 9+W 10 <= 80, 000 (total square feet) W 1 -10000 Y 1 <= 0 W 2 -12000 Y 2 <= 0 W 3 -20000 Y 3 <= 0 W 4 -20000 Y 4 <= 0 W 5 -20000 Y 5 <= 0 W 6 -20000 Y 6 <= 0 W 7 -20000 Y 7 <= 0 W 8 -15000 Y 8 <= 0 W 9 -15000 Y 9 <= 0 W 10 -10000 Y 10 <=0

More Constraints no more than 5 stores Y 1+Y 2+Y 3+Y 4+Y 5+Y 6+Y 7+Y 8+Y 9+Y 10 <= 5 180000 Y 1+55 W 1+120000 Y 2+62 W 2+95000 Y 3+67 W 3+125000 Y 4+70 W 4+980 00 Y 5+64 W 5+114000 Y 6+64 W 6+88000 Y 7+58 W 7+91000 Y 8+55 W 8+97000 Y 9+ 60 W 9+102000 Y 10+57 W 10 <=5, 000 (construction budget) Stores within 10 miles Y 1+Y 2 <= 1 Y 1+Y 3 <= 1 Y 2+Y 4 <= 1 Y 6+Y 1 <= 1
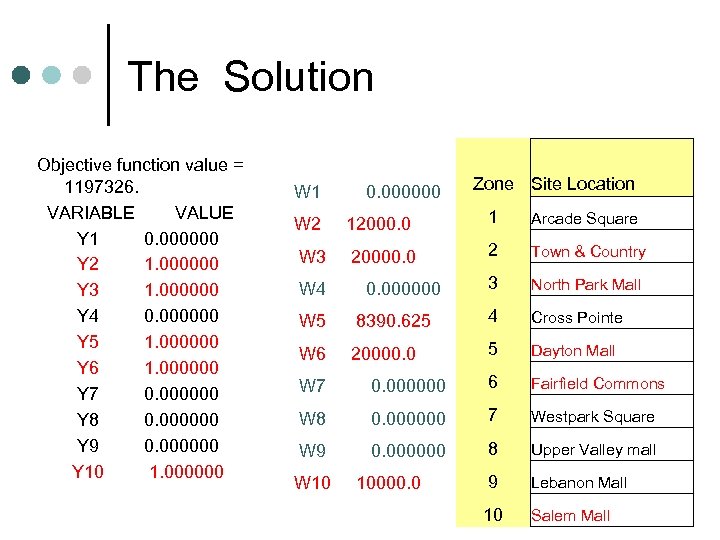
The Solution Objective function value = 1197326. VARIABLE VALUE Y 1 0. 000000 Y 2 1. 000000 Y 3 1. 000000 Y 4 0. 000000 Y 5 1. 000000 Y 6 1. 000000 Y 7 0. 000000 Y 8 0. 000000 Y 9 0. 000000 Y 10 1. 000000 W 1 0. 000000 Zone Site Location 1 Arcade Square W 2 12000. 0 W 3 20000. 0 2 Town & Country W 4 0. 000000 3 North Park Mall W 5 8390. 625 4 Cross Pointe W 6 20000. 0 5 Dayton Mall W 7 0. 000000 6 Fairfield Commons W 8 0. 000000 7 Westpark Square W 9 0. 000000 8 Upper Valley mall W 10 10000. 0 9 10 Lebanon Mall Salem Mall
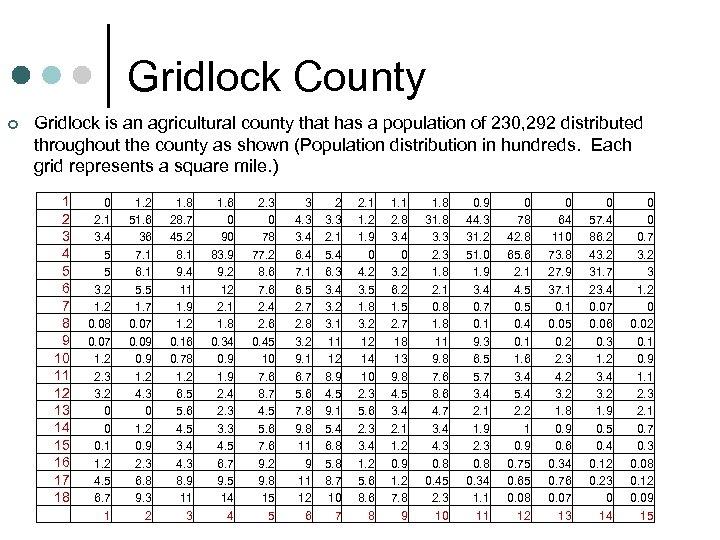
Gridlock County ¢ Gridlock is an agricultural county that has a population of 230, 292 distributed throughout the county as shown (Population distribution in hundreds. Each grid represents a square mile. ) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 2. 1 3. 4 5 5 3. 2 1. 2 0. 08 0. 07 1. 2 2. 3 3. 2 0 0 0. 1 1. 2 4. 5 6. 7 1 1. 2 51. 6 36 7. 1 6. 1 5. 5 1. 7 0. 09 0. 9 1. 2 4. 3 0 1. 2 0. 9 2. 3 6. 8 9. 3 2 1. 8 28. 7 45. 2 8. 1 9. 4 11 1. 9 1. 2 0. 16 0. 78 1. 2 6. 5 5. 6 4. 5 3. 4 4. 3 8. 9 11 3 1. 6 0 90 83. 9 9. 2 12 2. 1 1. 8 0. 34 0. 9 1. 9 2. 4 2. 3 3. 3 4. 5 6. 7 9. 5 14 4 2. 3 0 78 77. 2 8. 6 7. 6 2. 4 2. 6 0. 45 10 7. 6 8. 7 4. 5 5. 6 7. 6 9. 2 9. 8 15 5 3 4. 3 3. 4 6. 4 7. 1 6. 5 2. 7 2. 8 3. 2 9. 1 6. 7 5. 6 7. 8 9. 8 11 9 11 12 6 2 3. 3 2. 1 5. 4 6. 3 3. 4 3. 2 3. 1 11 12 8. 9 4. 5 9. 1 5. 4 6. 8 5. 8 8. 7 10 7 2. 1 1. 2 1. 9 0 4. 2 3. 5 1. 8 3. 2 12 14 10 2. 3 5. 6 2. 3 3. 4 1. 2 5. 6 8 1. 1 2. 8 3. 4 0 3. 2 6. 2 1. 5 2. 7 18 13 9. 8 4. 5 3. 4 2. 1 1. 2 0. 9 1. 2 7. 8 9 1. 8 3. 3 2. 3 1. 8 2. 1 0. 8 11 9. 8 7. 6 8. 6 4. 7 3. 4 4. 3 0. 8 0. 45 2. 3 10 0. 9 44. 3 31. 2 51. 0 1. 9 3. 4 0. 7 0. 1 9. 3 6. 5 5. 7 3. 4 2. 1 1. 9 2. 3 0. 8 0. 34 1. 1 11 0 78 42. 8 65. 6 2. 1 4. 5 0. 4 0. 1 1. 6 3. 4 5. 4 2. 2 1 0. 9 0. 75 0. 65 0. 08 12 0 64 110 73. 8 27. 9 37. 1 0. 05 0. 2 2. 3 4. 2 3. 2 1. 8 0. 9 0. 6 0. 34 0. 76 0. 07 13 0 57. 4 86. 2 43. 2 31. 7 23. 4 0. 07 0. 06 0. 3 1. 2 3. 4 3. 2 1. 9 0. 5 0. 4 0. 12 0. 23 0 14 0 0 0. 7 3. 2 3 1. 2 0 0. 02 0. 1 0. 9 1. 1 2. 3 2. 1 0. 7 0. 3 0. 08 0. 12 0. 09 15

The Problem ¢ ¢ A countywide program to inoculate the entire population against the dreaded N 1 H 1 virus is to begin shortly. The county health officials want to conduct the immunizations in the most convenient location within the county. Convenience is defined to be that location that will minimize the total miles traveled by all the residents of Gridlock County. (a) Approximating travel within the County as straight-line from one point to another, determine the most convenient location (grid) for conducting the immunizations. (b) Approximating travel within the County as rectilinear (horizontal and vertical travel only) from one point to another, determine the most convenient location (grid) for conducting the immunizations. Assume the entire population within each grid is located at the center of the grid.
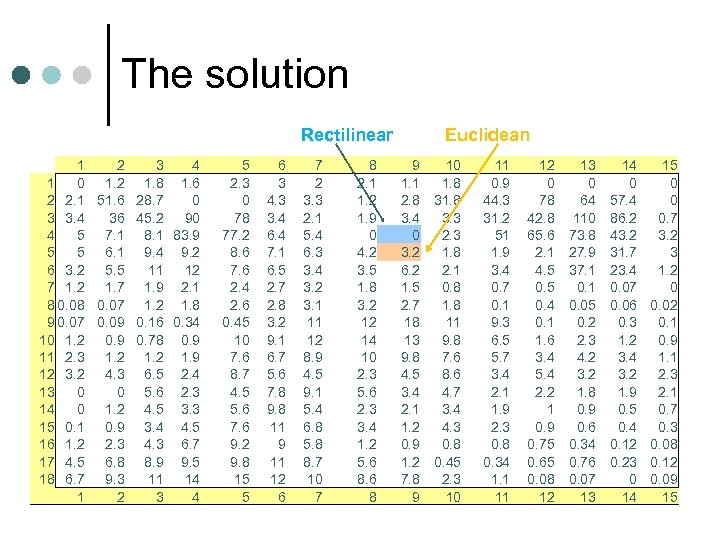
The solution Rectilinear 1 2 3 4 1 0 1. 2 1. 8 1. 6 2 2. 1 51. 6 28. 7 0 3 3. 4 36 45. 2 90 4 5 7. 1 83. 9 5 5 6. 1 9. 4 9. 2 6 3. 2 5. 5 11 12 7 1. 2 1. 7 1. 9 2. 1 8 0. 07 1. 2 1. 8 9 0. 07 0. 09 0. 16 0. 34 10 1. 2 0. 9 0. 78 0. 9 11 2. 3 1. 2 1. 9 12 3. 2 4. 3 6. 5 2. 4 13 0 0 5. 6 2. 3 14 0 1. 2 4. 5 3. 3 15 0. 1 0. 9 3. 4 4. 5 16 1. 2 2. 3 4. 3 6. 7 17 4. 5 6. 8 8. 9 9. 5 18 6. 7 9. 3 11 14 1 2 3 4 5 2. 3 0 78 77. 2 8. 6 7. 6 2. 4 2. 6 0. 45 10 7. 6 8. 7 4. 5 5. 6 7. 6 9. 2 9. 8 15 5 6 3 4. 3 3. 4 6. 4 7. 1 6. 5 2. 7 2. 8 3. 2 9. 1 6. 7 5. 6 7. 8 9. 8 11 9 11 12 6 7 2 3. 3 2. 1 5. 4 6. 3 3. 4 3. 2 3. 1 11 12 8. 9 4. 5 9. 1 5. 4 6. 8 5. 8 8. 7 10 7 8 2. 1 1. 2 1. 9 0 4. 2 3. 5 1. 8 3. 2 12 14 10 2. 3 5. 6 2. 3 3. 4 1. 2 5. 6 8 Euclidean 9 10 1. 1 1. 8 2. 8 31. 8 3. 4 3. 3 0 2. 3 3. 2 1. 8 6. 2 2. 1 1. 5 0. 8 2. 7 1. 8 18 11 13 9. 8 7. 6 4. 5 8. 6 3. 4 4. 7 2. 1 3. 4 1. 2 4. 3 0. 9 0. 8 1. 2 0. 45 7. 8 2. 3 9 10 11 0. 9 44. 3 31. 2 51 1. 9 3. 4 0. 7 0. 1 9. 3 6. 5 5. 7 3. 4 2. 1 1. 9 2. 3 0. 8 0. 34 1. 1 11 12 0 78 42. 8 65. 6 2. 1 4. 5 0. 4 0. 1 1. 6 3. 4 5. 4 2. 2 1 0. 9 0. 75 0. 65 0. 08 12 13 0 64 110 73. 8 27. 9 37. 1 0. 05 0. 2 2. 3 4. 2 3. 2 1. 8 0. 9 0. 6 0. 34 0. 76 0. 07 13 14 0 57. 4 86. 2 43. 2 31. 7 23. 4 0. 07 0. 06 0. 3 1. 2 3. 4 3. 2 1. 9 0. 5 0. 4 0. 12 0. 23 0 14 15 0 0 0. 7 3. 2 3 1. 2 0 0. 02 0. 1 0. 9 1. 1 2. 3 2. 1 0. 7 0. 3 0. 08 0. 12 0. 09 15
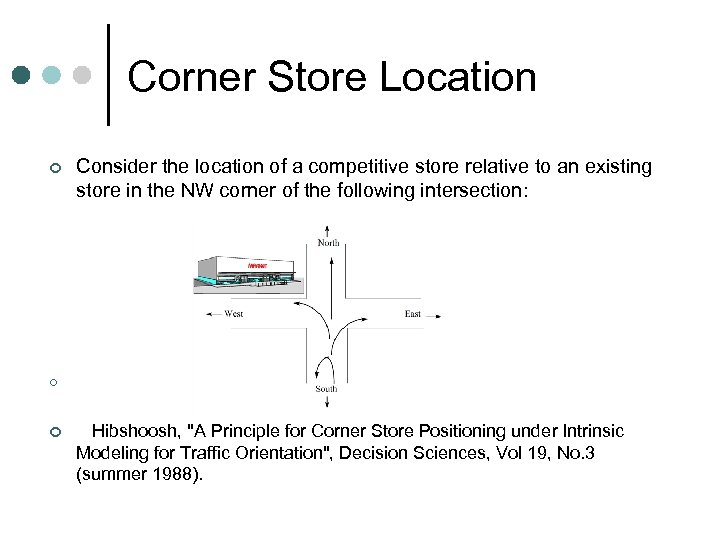
Corner Store Location ¢ Consider the location of a competitive store relative to an existing store in the NW corner of the following intersection: ¢ ¢ Hibshoosh, "A Principle for Corner Store Positioning under Intrinsic Modeling for Traffic Orientation", Decision Sciences, Vol 19, No. 3 (summer 1988).

The Rules of the Road Assume perfectly symmetrical traffic flows from all four directions, and upon arrival at the intersection, a vehicle performs one of the following traffic movements: (1) continues forward, (2) turns right, (3) turns left, or (4) makes a U-turn (assume legal). Let Pi = probability of approaching intersection from direction i, i = N, S, E, AND W. Then P 1 = P 2 = P 3 = P 4 = 1/4. Pj = probability of executing traffic movement j (j = 1, 2, 3, or 4), then assume P 1 > P 2 > P 3 > P 4 represents the drivers preference for turning movements. Further. assume a fixed proportion, c, of drivers who will pass a store will stop and make a purchase at that store. Let N represents the number of vehicles entering the intersection per hour, and K represents the average profit per buyer at the store. Then S = c. NK is the average profit per vehicle per time period.
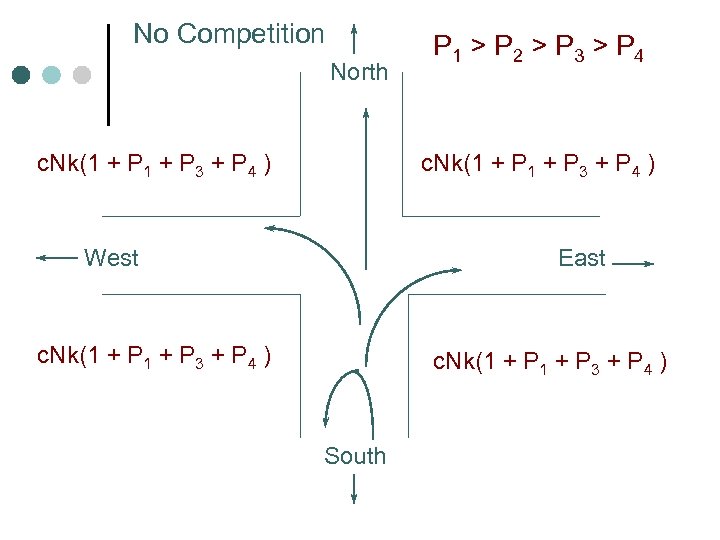
No Competition North c. Nk(1 + P 3 + P 4 ) P 1 > P 2 > P 3 > P 4 c. Nk(1 + P 3 + P 4 ) West East c. Nk(1 + P 3 + P 4 ) South
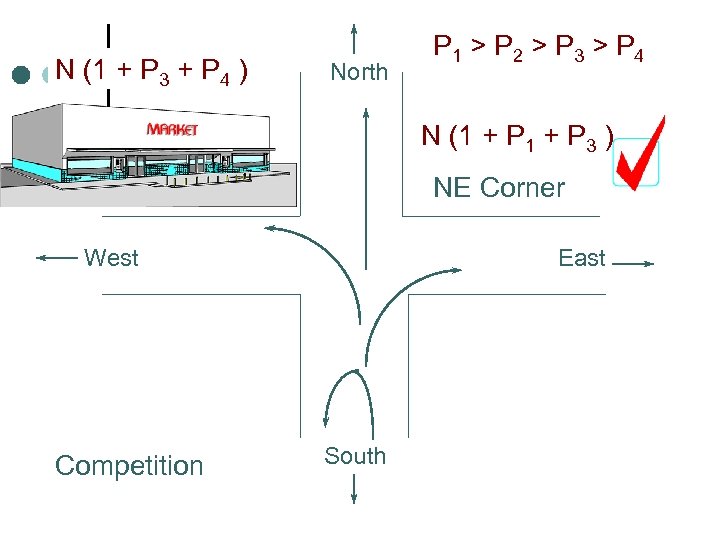
N (1 + P 3 + P 4 ) North P 1 > P 2 > P 3 > P 4 N (1 + P 3 ) NE Corner West Competition East South
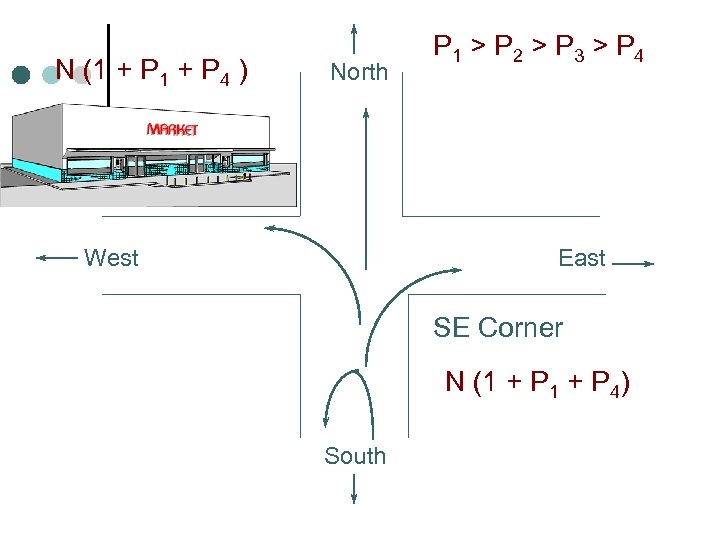
N (1 + P 4 ) North West P 1 > P 2 > P 3 > P 4 East SE Corner N (1 + P 4) South
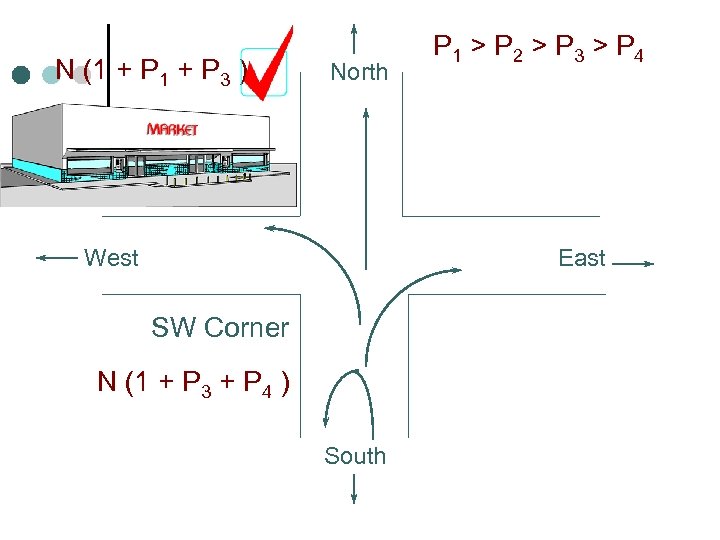
N (1 + P 3 ) North West P 1 > P 2 > P 3 > P 4 East SW Corner N (1 + P 3 + P 4 ) South

Towards a Science of Management Science A Law of Corner Store Location All other factors being equal, a convenience corner store should be positioned clockwise adjacent to the already established rival store.
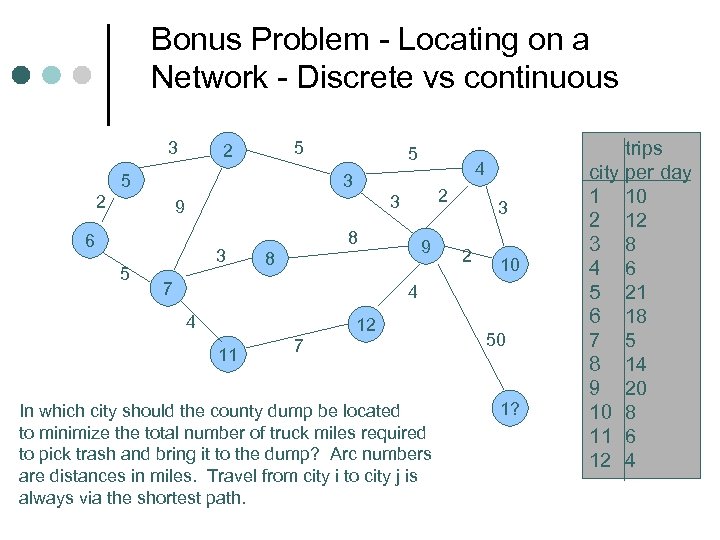
Bonus Problem - Locating on a Network - Discrete vs continuous 3 5 2 5 5 2 2 3 9 6 5 4 3 3 8 9 8 7 3 2 10 4 4 12 11 7 In which city should the county dump be located to minimize the total number of truck miles required to pick trash and bring it to the dump? Arc numbers are distances in miles. Travel from city i to city j is always via the shortest path. 50 1? trips city per day 1 10 2 12 3 8 4 6 5 21 6 18 7 5 8 14 9 20 10 8 11 6 12 4
e801e780672f2d9f1025ddf7cc31ee7f.ppt