82168227084aa5d9b0bbc5ac4cf0abc1.ppt
- Количество слайдов: 74

“A bank is a place that will lend you money if you can prove that you don’t need it. ” Bob Hope Saunders & Cornett, Financial Institutions Management, 4 th ed. 1

Why New Approaches to Credit Risk Measurement and Management? Why Now? Saunders & Cornett, Financial Institutions Management, 4 th ed. 2

Structural Increase in Bankruptcy • Increase in probability of default – High yield default rates: 5. 1% (2000), 4. 3% (1999, 1. 9% (1998). Source: Fitch 3/19/01 – Historical Default Rates: 6. 92% (3 Q 2001), 5. 065% (2000), 4. 147% (1999), 1998 (1. 603%), 1997 (1. 252%), 10. 273% (1991), 10. 14% (1990). Source: Altman • Increase in Loss Given Default (LGD) – First half of 2001 defaulted telecom junk bonds recovered average 12 cents per $1 ($0. 25 in 1999 -2000) • Only 9 AAA Firms in US: Merck, Bristol-Myers, Squibb, GE, Exxon Mobil, Berkshire Hathaway, AIG, J&J, Pfizer, UPS. Late 70 s: 58 firms. Early 90 s: 22 firms. Saunders & Cornett, Financial Institutions Management, 4 th ed. 3

Disintermediation • Direct Access to Credit Markets – 20, 000 US companies have access to US commercial paper market. – Junk Bonds, Private Placements. • “Winner’s Curse” – Banks make loans to borrowers without access to credit markets. Saunders & Cornett, Financial Institutions Management, 4 th ed. 4

More Competitive Margins • Worsening of the risk-return tradeoff – Interest Margins (Spreads) have declined • Ex: Secondary Loan Market: Largest mutual funds investing in bank loans (Eaton Vance Prime Rate Reserves, Van Kampen Prime Rate Income, Franklin Floating Rate, MSDW Prime Income Trust): 5 -year average returns 5. 45% and 6/30/006/30/01 returns of only 2. 67% – Average Quality of Loans have deteriorated • The loan mutual funds have written down loan value Saunders & Cornett, Financial Institutions Management, 4 th ed. 5

The Growth of Off-Balance Sheet Derivatives • Total on-balance sheet assets for all US banks = $5 trillion (Dec. 2000) and for all Euro banks = $13 trillion. • Value of non-government debt & bond markets worldwide = $12 trillion. • Global Derivatives Markets > $84 trillion. • All derivatives have credit exposure. • Credit Derivatives. Saunders & Cornett, Financial Institutions Management, 4 th ed. 6

Declining and Volatile Values of Collateral • Worldwide deflation in real asset prices. – Ex: Japan and Switzerland – Lending based on intangibles – ex. Enron. Saunders & Cornett, Financial Institutions Management, 4 th ed. 7

Technology • Computer Information Technology – Models use Monte Carlo Simulations that are computationally intensive • Databases – Commercial Databases such as Loan Pricing Corporation – ISDA/IIF Survey: internal databases exist to measure credit risk on commercial, retail, mortgage loans. Not emerging market debt. Saunders & Cornett, Financial Institutions Management, 4 th ed. 8

BIS Risk-Based Capital Requirements • BIS I: Introduced risk-based capital using 8% “one size fits all” capital charge. • Market Risk Amendment: Allowed internal models to measure VAR for tradable instruments & portfolio correlations – the “ 1 bad day in 100” standard. • Proposed New Capital Accord BIS II – Links capital charges to external credit ratings or internal model of credit risk. To be implemented in 2005. Saunders & Cornett, Financial Institutions Management, 4 th ed. 9

Traditional Approaches to Credit Risk Measurement 20 years of modeling history Saunders & Cornett, Financial Institutions Management, 4 th ed. 10

Expert Systems – The 5 Cs • • Character – reputation, repayment history Capital – equity contribution, leverage. Capacity – Earnings volatility. Collateral – Seniority, market value & volatility of MV of collateral. • Cycle – Economic conditions. – 1990 -91 recession default rates >10%, 1992 -1999: < 3% p. a. Altman & Saunders (2001) – Non-monotonic relationship between interest rates & excess returns. Stiglitz-Weiss adverse selection & risk shifting. Saunders & Cornett, Financial 11 Institutions Management, 4 th ed.

Problems with Expert Systems • Consistency – Across borrower. “Good” customers are likely to be treated more leniently. “A rolling loan gathers no loss. ” – Across expert loan officer. Loan review committees try to set standards, but still may vary. – Dispersion in accuracy across 43 loan officers evaluating 60 loans: accuracy rate ranged from 27 -50. Libby (1975), Libby, Trotman & Zimmer (1987). • Subjectivity – What are the optimal weights to assign to each factor? Saunders & Cornett, Financial Institutions Management, 4 th ed. 12

Credit Scoring Models • • • Linear Probability Model Logit Model Probit Model Discriminant Analysis Model 97% of banks use to approve credit card applications, 70% for small business lending, but only 8% of small banks (<$5 billion in assets) use for small business loans. Mester (1997). Saunders & Cornett, Financial Institutions Management, 4 th ed. 13

Linear Discriminant Analysis – The Altman Z-Score Model • Z-score (probability of default) is a function of: – – – Working capital/total assets ratio (1. 2) Retained earnings/assets (1. 4) EBIT/Assets ratio (3. 3) Market Value of Equity/Book Value of Debt (0. 6) Sales/Total Assets (1. 0) Critical Value: 1. 81 Saunders & Cornett, Financial Institutions Management, 4 th ed. 14

Problems with Credit Scoring • Assumes linearity. • Based on historical accounting ratios, not market values (with exception of market to book ratio). – Not responsive to changing market conditions. – 56% of the 33 banks that used credit scoring for credit card applications failed to predict loan quality problems. Mester (1998). • Lack of grounding in economic theory. Saunders & Cornett, Financial Institutions Management, 4 th ed. 15

The Option Theoretic Model of Credit Risk Measurement Based on Merton (1974) KMV Proprietary Model Saunders & Cornett, Financial Institutions Management, 4 th ed. 16

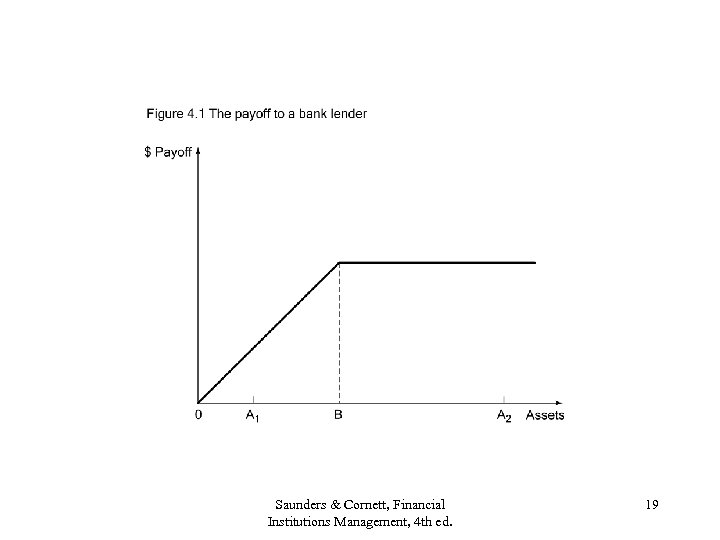
The Link Between Loans and Optionality: Merton (1974) • Figure 4. 1: Payoff on pure discount bank loan with face value=0 B secured by firm asset value. – Firm owners repay loan if asset value (upon loan maturity) exceeds 0 B (eg. , 0 A 2). Bank receives full principal + interest payment. – If asset value < 0 B then default. Bank receives assets. Saunders & Cornett, Financial Institutions Management, 4 th ed. 17

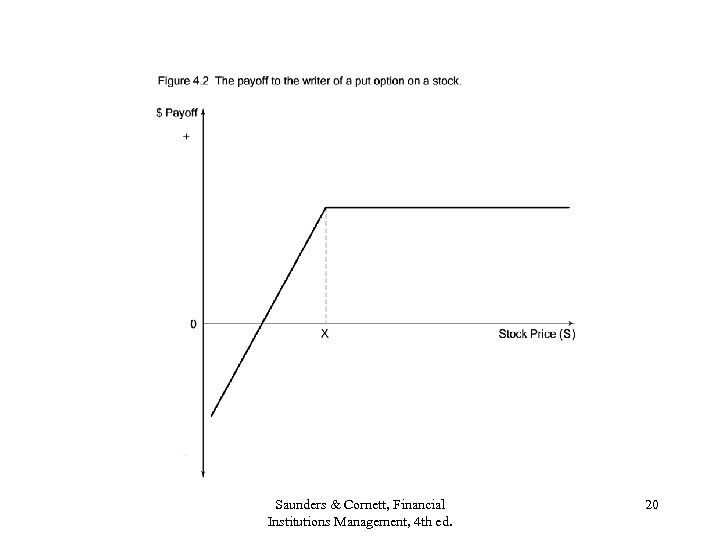
Using Option Valuation Models to Value Loans • Figure 4. 1 loan payoff = Figure 4. 2 payoff to the writer of a put option on a stock. • Value of put option on stock = equation (4. 1) = f(S, X, r, , ) where S=stock price, X=exercise price, r=risk-free rate, =equity volatility, =time to maturity. Value of default option on risky loan = equation (4. 2) = f(A, B, r, A, ) where A=market value of assets, B=face value of debt, r=risk-free rate, A=asset volatility, =time to debt maturity. Saunders & Cornett, Financial Institutions Management, 4 th ed. 18
Saunders & Cornett, Financial Institutions Management, 4 th ed. 19
Saunders & Cornett, Financial Institutions Management, 4 th ed. 20

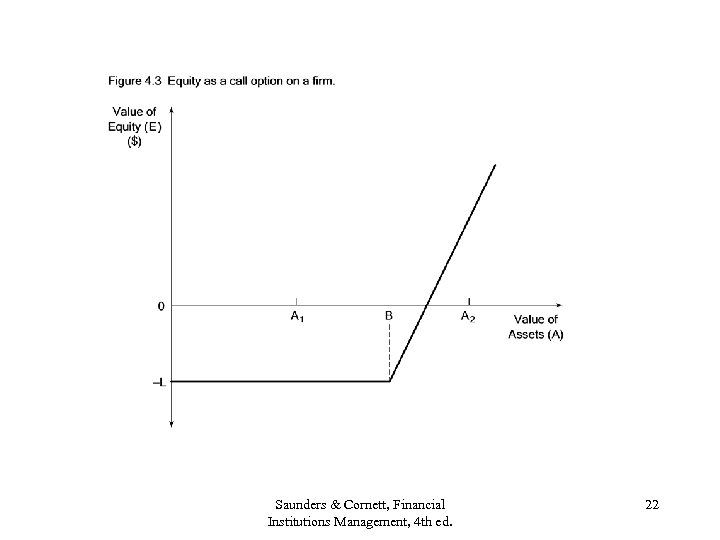
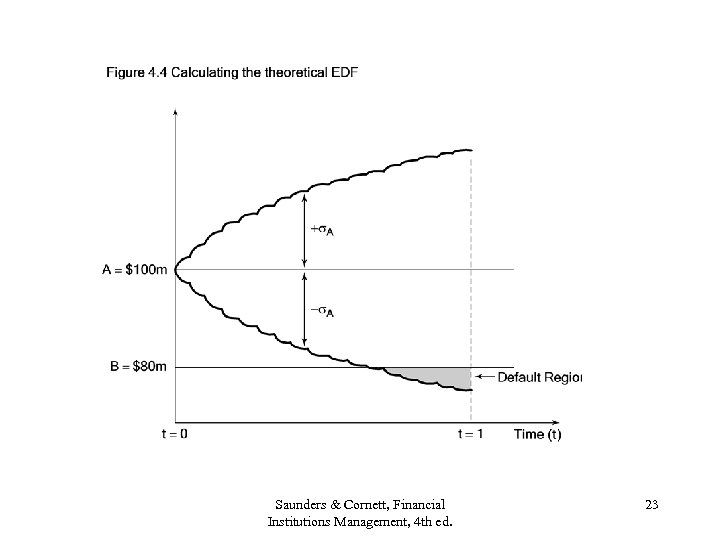
Problem with Equation (4. 2) • A and A are not observable. • Model equity as a call option on a firm. (Figure 4. 3) • Equity valuation = equation (4. 3) = E = h(A, A, B, r, ) Need another equation to solve for A and A: E = g( A) Equation (4. 4) Can solve for A and A with equations (4. 3) and (4. 4) to obtain a Distance to Default = (A-B)/ A Figure 4. 4 Saunders & Cornett, Financial Institutions Management, 4 th ed. 21
Saunders & Cornett, Financial Institutions Management, 4 th ed. 22
Saunders & Cornett, Financial Institutions Management, 4 th ed. 23

Merton’s Theoretical PD • • Assumes assets are normally distributed. Example: Assets=$100 m, Debt=$80 m, A=$10 m Distance to Default = (100 -80)/10 = 2 std. dev. There is a 2. 5% probability that normally distributed assets increase (fall) by more than 2 standard deviations from mean. So theoretical PD = 2. 5%. • But, asset values are not normally distributed. Fat tails and skewed distribution (limited upside gain). Saunders & Cornett, Financial Institutions Management, 4 th ed. 24

Merton’s Bond Valuation Model • B=$100, 000, =1 year, =12%, r=5%, leverage ratio (d)=90% • Substituting in Merton’s option valuation expression: – The current market value of the risky loan is $93, 866. 18 – The required risk premium = 1. 33% Saunders & Cornett, Financial Institutions Management, 4 th ed. 25

KMV’s Empirical EDF • Utilize database of historical defaults to calculate empirical PD (called EDF): • Fig. 4. 5 Saunders & Cornett, Financial Institutions Management, 4 th ed. 26
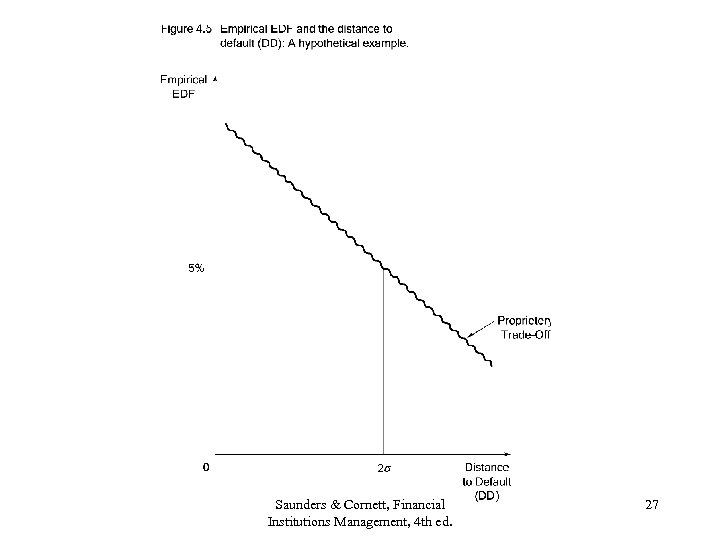
Saunders & Cornett, Financial Institutions Management, 4 th ed. 27

Accuracy of KMV EDFs Comparison to External Credit Ratings • • Enron (Figure 4. 8) Comdisco (Figure 4. 6) USG Corp. (Figure 4. 7) Power Curve (Figure 4. 9): Deny credit to the bottom 20% of all rankings: Type 1 error on KMV EDF = 16%; Type 1 error on S&P/Moody’s obligor-level ratings=22%; Type 1 error on issue-specific rating=35%. Saunders & Cornett, Financial Institutions Management, 4 th ed. 28

Saunders & Cornett, Financial Institutions Management, 4 th ed. 29

Monthly EDF™ credit measure Agency Rating Saunders & Cornett, Financial Institutions Management, 4 th ed. 30
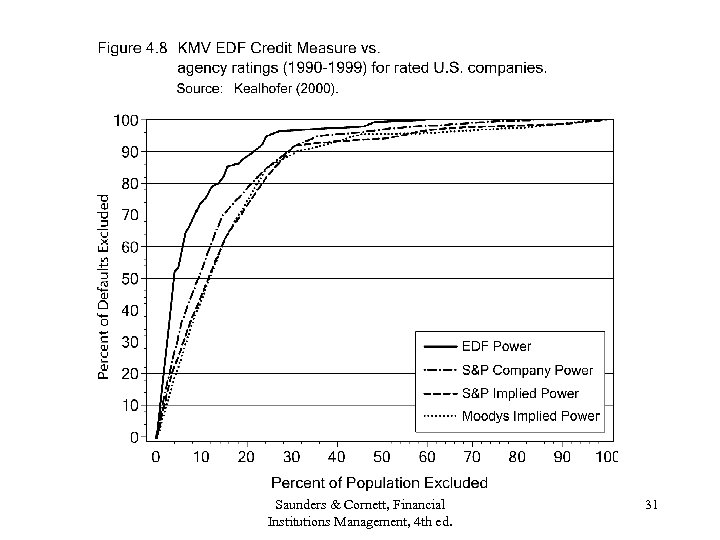
Saunders & Cornett, Financial Institutions Management, 4 th ed. 31

Problems with KMV EDF • Not risk-neutral PD: Understates PD since includes an asset expected return > risk-free rate. – Use CAPM to remove risk-adjusted rate of return. Derives risk-neutral EDF (denoted QDF). Bohn (2000). • Static model – assumes that leverage is unchanged. Mueller (2000) and Collin-Dufresne and Goldstein (2001) model leverage changes. • Does not distinguish between different types of debt – seniority, collateral, covenants, convertibility. Leland (1994), Anderson, Sundaresan and Tychon (1996) and Mella-Barral and Perraudin (1997) consider debt renegotiations and other frictions. • Suggests that credit spreads should tend to zero as time to maturity approaches zero. Duffie and Lando (2001) incomplete information model. Zhou (2001) jump diffusion model. Saunders & Cornett, Financial Institutions Management, 4 th ed. 32

Term Structure Derivation of Credit Risk Measures Reduced Form Models: KPMG’s Loan Analysis System and Kamakura’s Risk Manager Saunders & Cornett, Financial Institutions Management, 4 th ed. 33

Estimating PD: An Alternative Approach • Merton’s OPM took a structural approach to modeling default: default occurs when the market value of assets fall below debt value • Reduced form models: Decompose risky debt prices to estimate the stochastic default intensity function. No structural explanation of why default occurs. Saunders & Cornett, Financial Institutions Management, 4 th ed. 34

A Discrete Example: Deriving Risk-Neutral Probabilities of Default • B rated $100 face value, zero-coupon debt security with 1 year until maturity and fixed LGD=100%. Risk-free spot rate = 8% p. a. • Security P = 87. 96 = [100(1 -PD)]/1. 08 Solving (5. 1), PD=5% p. a. • Alternatively, 87. 96 = 100/(1+y) where y is the risk-adjusted rate of return. Solving (5. 2), y=13. 69% p. a. • (1+r) = (1 -PD)(1+y) or 1. 08=(1 -. 05)(1. 1369) Saunders & Cornett, Financial Institutions Management, 4 th ed. 35

Multiyear PD Using Forward Rates • Using the expectations hypothesis, the yield curves in Figure 5. 1 can be decomposed: • (1+0 y 2)2 = (1+0 y 1)(1+1 y 1) or 1. 162=1. 1369(1+1 y 1) 1 y 1=18. 36% p. a. • (1+0 r 2)2 = (1+0 r 1)(1+1 r 1) or 1. 102=1. 08(1+1 r 1) 1 r 1=12. 04% p. a. • One year forward PD=5. 34% p. a. from: (1+r) = (1 - PD)(1+y) 1. 1204=1. 1836(1 – PD) • Cumulative PD = 1 – [(1 - PD 1)(1 – PD 2)] = 1 – [(1 -. 05)(1 -. 0534)] = 10. 07% Saunders & Cornett, Financial Institutions Management, 4 th ed. 36
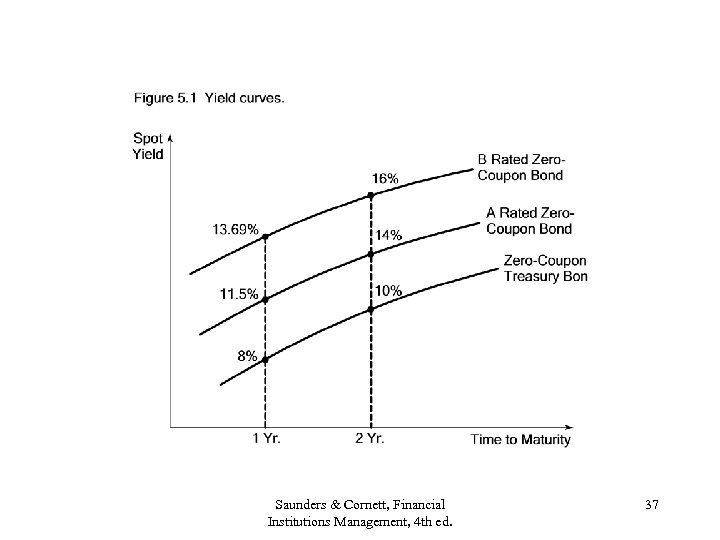
Saunders & Cornett, Financial Institutions Management, 4 th ed. 37

The Loss Intensity Process • Expected Losses (EL) = PD x LGD • If LGD is not fixed at 100% then: (1 + r) = [1 - (PDx. LGD)](1 + y) Identification problem: cannot disentangle PD from LGD. Saunders & Cornett, Financial Institutions Management, 4 th ed. 38

Disentangling PD from LGD • Intensity-based models specify stochastic functional form for PD. – Jarrow & Turnbull (1995): Fixed LGD, exponentially distributed default process. – Das & Tufano (1995): LGD proportional to bond values. – Jarrow, Lando & Turnbull (1997): LGD proportional to debt obligations. – Duffie & Singleton (1999): LGD and PD functions of economic conditions – Unal, Madan & Guntay (2001): LGD a function of debt seniority. – Jarrow (2001): LGD determined using equity prices. Saunders & Cornett, Financial Institutions Management, 4 th ed. 39

KPMG’s Loan Analysis System • Uses risk-neutral pricing grid to mark-to-market • Backward recursive iterative solution – Figure 5. 2. • Example: Consider a $100 2 year zero coupon loan with LGD=100% and yield curves from Figure 5. 1. • Year 1 Node (Figure 5. 3): – Valuation at B rating = $84. 79 =. 94(100/1. 1204) +. 01(100/1. 1204) +. 05(0) – Valuation at A rating = $88. 95 =. 94(100/1. 1204) +. 0566(100/1. 1204) +. 0034(0) • Year 0 Node = $74. 62 =. 94(84. 79/1. 08) +. 01(88. 95/1. 08) • Calculating a credit spread: 74. 62 = 100/[(1. 08+CS)(1. 1204+CS)] to get CS=5. 8% p. a. Saunders & Cornett, Financial Institutions Management, 4 th ed. 40

Saunders & Cornett, Financial Institutions Management, 4 th ed. 41

Saunders & Cornett, Financial Institutions Management, 4 th ed. 42

Noisy Risky Debt Prices • US corporate bond market is much larger than equity market, but less transparent • Interdealer market not competitive – large spreads and infrequent trading: Saunders, Srinivasan & Walter (2002) • Noisy prices: Hancock & Kwast (2001) • More noise in senior than subordinated issues: Bohn (1999) • In addition to credit spreads, bond yields include: – Liquidity premium – Embedded options – Tax considerations and administrative costs of holding risky debt Saunders & Cornett, Financial 43 Institutions Management, 4 th ed.

Mortality Rate Derivation of Credit Risk Measures The Insurance Approach: Mortality Models and the CSFP Credit Risk Plus Model Saunders & Cornett, Financial Institutions Management, 4 th ed. 44

Mortality Analysis • Marginal Mortality Rates = (total value of B -rated bonds defaulting in yr 1 of issue)/(total value of B-rated bonds in yr 1 of issue). • Do for each year of issue. • Weighted Average MMR = MMRi = t. MMRt x w where w is the size weight for each year t. Saunders & Cornett, Financial Institutions Management, 4 th ed. 45

Mortality Rates - Table 11. 10 • Cumulative Mortality Rates (CMR) are calculated as: – MMRi = 1 – SRi where SRi is the survival rate defined as 1 -MMRi in ith year of issue. – CMRT = 1 – (SR 1 x SR 2 x…x SRT) over the T years of calculation. – Standard deviation = [MMRi(1 -MMRi)/n] As the number of bonds in the sample n increases, the standard error falls. Can calculate the number of observations needed to reduce error rate to say std. dev. =. 001 – No. of obs. = MMRi(1 -MMRi)/ 2 = (. 01)(. 99)/(. 001)2 = 9, 900 Saunders & Cornett, Financial Institutions Management, 4 th ed. 46

CSFP Credit Risk Plus Appendix 11 B • Default model • Credit. Metrics: default probability is discrete (from transition matrix). In Credit. Risk +, default is a continuous variable with a probability distribution. • Default probabilities are independent across loans. • Loan portfolio’s default probability follows a Poisson distribution. See Fig. 8. 1. • Variance of PD = mean default rate. • Loss severity (LGD) is also stochastic in Credit Risk +. Saunders & Cornett, Financial Institutions Management, 4 th ed. 47
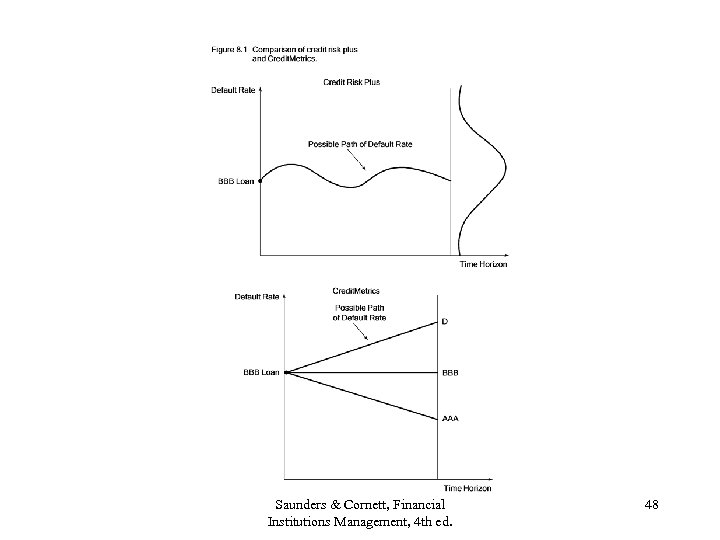
Saunders & Cornett, Financial Institutions Management, 4 th ed. 48

Saunders & Cornett, Financial Institutions Management, 4 th ed. 49

Distribution of Losses • Combine default frequency and loss severity to obtain a loss distribution. Figure 8. 3. • Loss distribution is close to normal, but with fatter tails. • Mean default rate of loan portfolio equals its variance. (property of Poisson distrib. ) Saunders & Cornett, Financial Institutions Management, 4 th ed. 50

Saunders & Cornett, Financial Institutions Management, 4 th ed. 51

Saunders & Cornett, Financial Institutions Management, 4 th ed. 52

Pros and Cons • Pro: Simplicity and low data requirements – just need mean loss rates and loss severities. • Con: Inaccuracy if distributional assumptions are violated. Saunders & Cornett, Financial Institutions Management, 4 th ed. 53

Divide Loan Portfolio Into Exposure Bands • In $20, 000 increments. • Group all loans that have $20, 000 of exposure (PDx. LGD), $40, 000 of exposure, etc. • Say 100 loans have $20, 000 of exposure. • Historical default rate for this exposure class = 3%, distributed according to Poisson distrib. Saunders & Cornett, Financial Institutions Management, 4 th ed. 54

Properties of Poisson Distribution • Prob. (n defaults in $20, 000 severity band) = (e-mmn)/n! Where: m=mean number of defaults. So: if m=3, then prob(3 defaults) = 22. 4% and prob(8 defaults)=0. 8%. • Table 8. 2 shows the cumulative probability of defaults for different values of n. • Fig. 8. 5 shows the distribution of the default probability for the $20, 000 band. Saunders & Cornett, Financial Institutions Management, 4 th ed. 55

Saunders & Cornett, Financial Institutions Management, 4 th ed. 56

Loss Probabilities for $20, 000 Severity Band Saunders & Cornett, Financial Institutions Management, 4 th ed. 57

Economic Capital Calculations • Expected losses in the $20, 000 band are $60, 000 (=3 x$20, 000) • Consider the 99. 6% Va. R: The probability that losses exceed this Va. R = 0. 4%. That is the probability that 8 loans or more default in the $20, 000 band. Va. R is the minimum loss in the 0. 4% region = 8 x $20, 000 = $160, 000. • Unexpected Losses = $160, 000 – 60, 000 = $100, 000 = economic capital. Saunders & Cornett, Financial Institutions Management, 4 th ed. 58
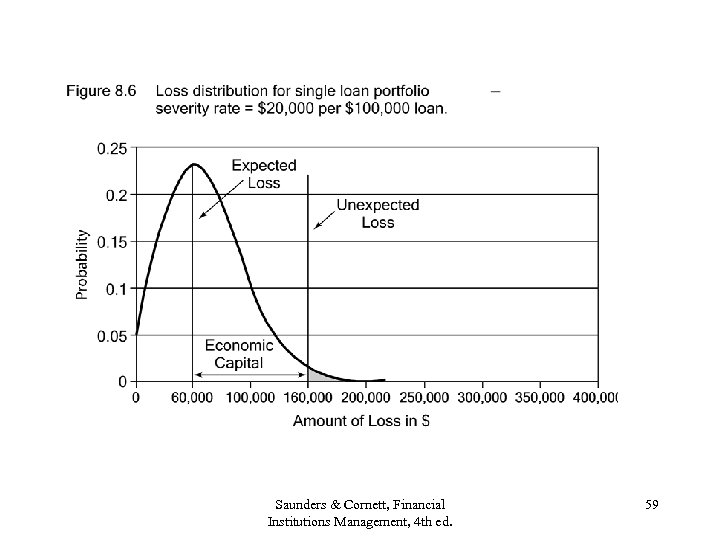
Saunders & Cornett, Financial Institutions Management, 4 th ed. 59

Saunders & Cornett, Financial Institutions Management, 4 th ed. 60

Calculating the Loss Distribution of a Portfolio Consisting of 2 Bands: $20, 000 and $40, 000 Loss Severity Saunders & Cornett, Financial Institutions Management, 4 th ed. 61

Add Another Severity Band • • Assume average loss exposure of $40, 000 100 loans in the $40, 000 band Assume a historic default rate of 3% Combining the $20, 000 and the $40, 000 loss severity bands makes the loss distribution more “normal. ” Fig. 8. 8. Saunders & Cornett, Financial Institutions Management, 4 th ed. 62
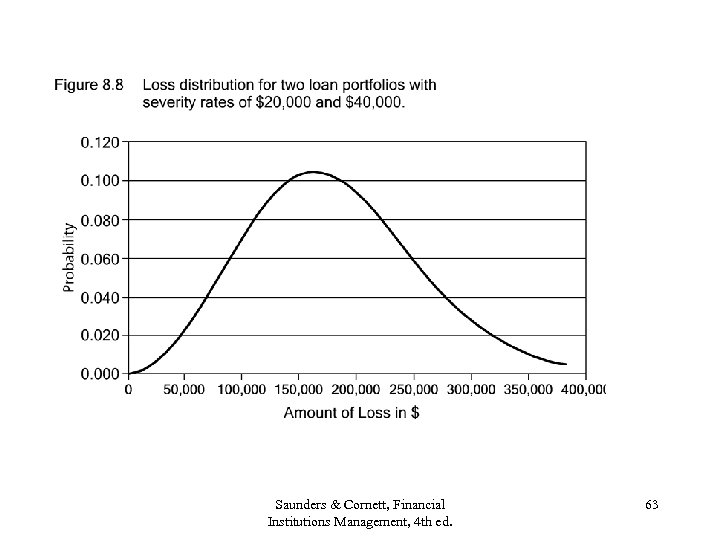
Saunders & Cornett, Financial Institutions Management, 4 th ed. 63

Oversimplifications • The mean default rate was assumed constant in each severity band. Should be a function of macroeconomic conditions. • Ignores default correlations – particularly during business cycles. Saunders & Cornett, Financial Institutions Management, 4 th ed. 64

Loan Portfolio Selection and Risk Measurement Chapter 12 Saunders & Cornett, Financial Institutions Management, 4 th ed. 65

The Paradox of Credit • Lending is not a “buy and hold”process. • To move to the efficient frontier, maximize return for any given level of risk or equivalently, minimize risk for any given level of return. • This may entail the selling of loans from the portfolio. “Paradox of Credit” – Fig. 10. 1. Saunders & Cornett, Financial Institutions Management, 4 th ed. 66
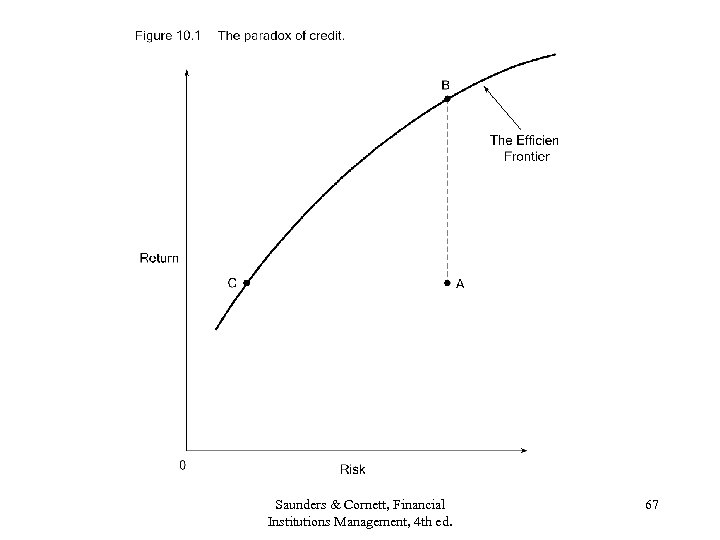
Saunders & Cornett, Financial Institutions Management, 4 th ed. 67

Managing the Loan Portfolio According to the Tenets of Modern Portfolio Theory • Improve the risk-return tradeoff by: – Calculating default correlations across assets. – Trade the loans in the portfolio (as conditions change) rather than hold the loans to maturity. – This requires the existence of a low transaction cost, liquid loan market. – Inputs to MPT model: Expected return, Risk (standard deviation) and correlations Saunders & Cornett, Financial Institutions Management, 4 th ed. 68

The Optimum Risky Loan Portfolio – Fig. 10. 2 • Choose the point on the efficient frontier with the highest Sharpe ratio: – The Sharpe ratio is the excess return to risk ratio calculated as: Saunders & Cornett, Financial Institutions Management, 4 th ed. 69

Saunders & Cornett, Financial Institutions Management, 4 th ed. 70

Problems in Applying MPT to Untraded Loan Portfolios • Mean-variance world only relevant if security returns are normal or if investors have quadratic utility functions. – Need 3 rd moment (skewness) and 4 th moment (kurtosis) to represent loan return distributions. • Unobservable returns – No historical price data. • Unobservable correlations Saunders & Cornett, Financial Institutions Management, 4 th ed. 71

KMV’s Portfolio Manager • Returns for each loan I: – Rit = Spreadi + Feesi – (EDFi x LGDi) – rf • Loan Risks=variability around EL=EGF x LGD = UL – LGD assumed fixed: ULi = – LGD variable, but independent across borrowers: ULi = – VOL is the standard deviation of LGD. VVOL is valuation volatility of loan value under MTM model. – MTM model with variable, indep LGD (mean LGD): ULi = Saunders & Cornett, Financial Institutions Management, 4 th ed. 72

Correlations • Figure 11. 2 – joint PD is the shaded area. • GF = GF/ G F • GF = • Correlations higher (lower) if isocircles are more elliptical (circular). • If JDFGF = EDFGEDFF then correlation=0. Saunders & Cornett, Financial Institutions Management, 4 th ed. 73

Saunders & Cornett, Financial Institutions Management, 4 th ed. 74
82168227084aa5d9b0bbc5ac4cf0abc1.ppt