A B C Теорема 1 Через прямую

Зарегистрируйтесь, чтобы просмотреть полный документ!

A B C

Теорема 1 Через прямую и точку, не лежащую на ней, проходит плоскость, и притом только одна. Дано: a; A ∉ a; Доказать: 1. ∃β: a ∊ β, A ∊ β; 2. β – единственная. Доказательство. 1. B ∊ a; C ∊ a; A, B, C – не лежат на одной прямой; ∃β: (A, B, C) ∊ β; (Аксиома А 1) B ∊ a; ⟹ BC ∊ β; a ∊ β; (Аксиома А 2) C ∊ a; β – искомая плоскость. B a C A 2. Любая другая плоскость, проходящая через прямую a и точку A проходит через B, C и A. Через три точки проходит единственная плоскость (аксиома А 1). Поэтому плоскость совпадет с плоскостью β.

Теорема 2 Через две пересекающиеся прямые проходит плоскость, и притом только одна. Дано: a, b; b Доказать: 1. ∃ α : a ∊ β, b ∊ β; 2. α – единственная. Доказательство. 1. B ∊ b; A ∊ α; ⟹ b ∊ α; (Аксиома А 2) B ∊ α; α – искомая плоскость. A B a 2. ∃β: (a, b) ∊ β; β ≠ α; B ∊ β; β ≡α; α – единственная плоскость.

Задача 1. Дано: Точки A, B, C и D не лежат в одной плоскости. C Найти: Могут ли прямые AB и CD пересекаться? A Решение: Через AB и CD проходит единственная плоскость. противоречит условию; Ответ: Нет. B D

Задача 2. Дано: Верно ли утверждение: если две точки окружности лежат в плоскости, то вся окружность лежит в этой плоскости; Решение: A B

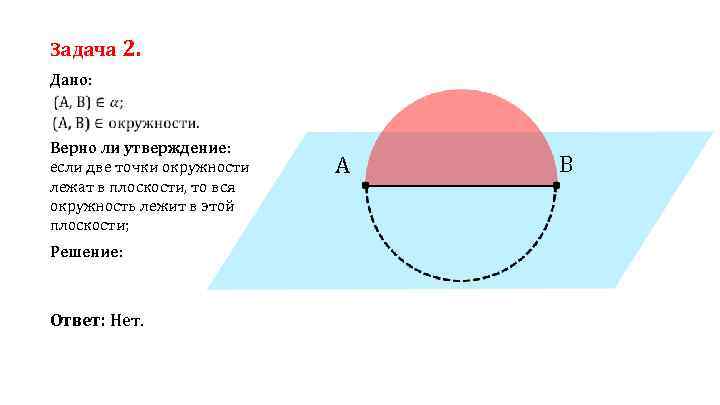
Задача 2. Дано: Верно ли утверждение: если две точки окружности лежат в плоскости, то вся окружность лежит в этой плоскости; Решение: Ответ: Нет. A A B B

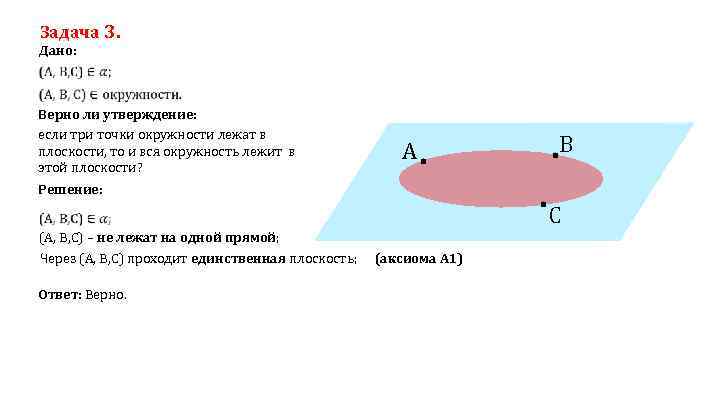
Задача 3. Дано: Верно ли утверждение: если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости? A B Решение: C (A, B, C) – не лежат на одной прямой; Через (A, B, C) проходит единственная плоскость; Ответ: Верно. (аксиома A 1)

Задача 4. Дано: M B Доказать: a, b – лежат в одной плоскости. Определить: лежат ли в одной плоскости a, b, d. Решение: (2 следствие аксиом) (аксиома А 2) – что и требовалось доказать. a d c A b

Скачать презентацию A B C Теорема 1 Через прямую

3. Некоторые следствия из аксиом.ppt

Количество слайдов: 8