
A & B A → B Основы логики B A ↔ v B A 2/5/2018

A→B Av. B A&B A&B Av. B A→B A&B v. B A A→B A&B B A→ Av. B A&B Логика – это наука о формах и способах мышления Джордж Буль (1815 -1864) основоположник математической логики 2

A→B Av. B A&B A&B Av. B A→B A&B v. B A A→B A&B B A→ Av. B A&B Содержание 1. Формы мышления 2. Алгебра высказываний 3. Логические выражения и таблицы истинности 4. Алгоритм построения таблиц истинности 5. Домашнее задание 6. Проверь себя 3

A→B Av. B A&B 1. Формы мышления A→B Av. B A&B Av. B A→B A&B v. B A A→B A&B B A→ Основные формы мышления: 1. Понятие 2. Высказывание 3. Умозаключение Av. B A&B содержание 4
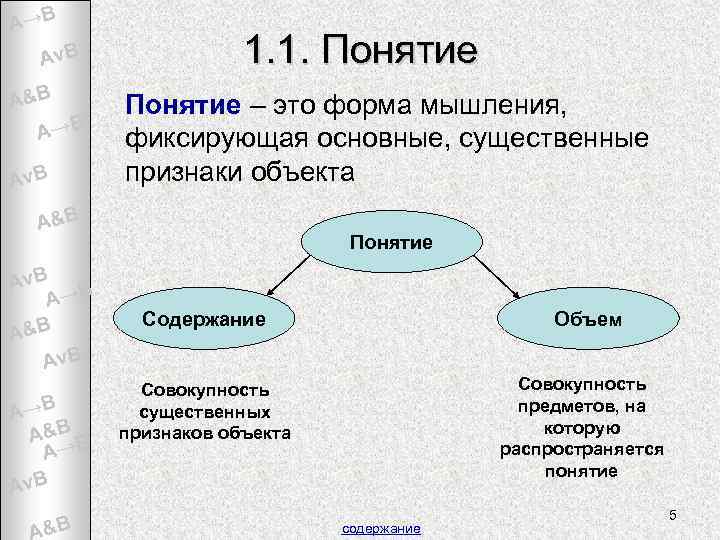
A→B Av. B A&B A→B Av. B 1. 1. Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта A&B Av. B A→B A&B v. B A A→B A&B B A→ Понятие Содержание Объем Совокупность предметов, на которую распространяется понятие Совокупность существенных признаков объекта Av. B A&B содержание 5
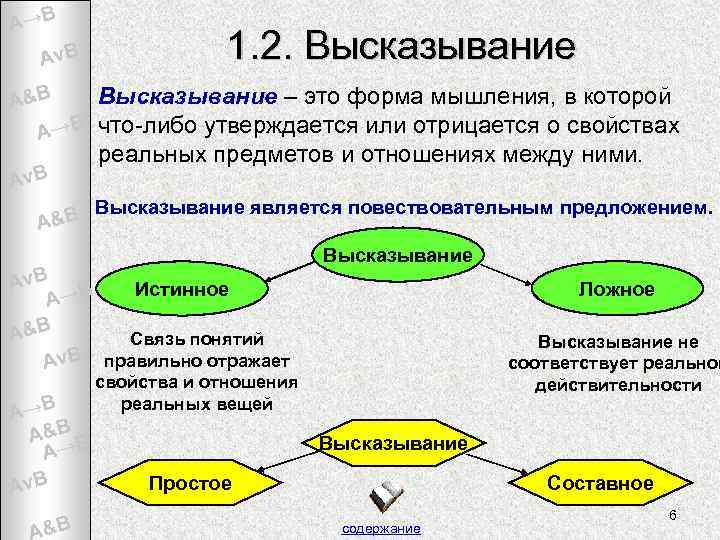
A→B Av. B 1. 2. Высказывание – это форма мышления, в которой A→B что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. A&B Av. B A&B Высказывание является повествовательным предложением. Av. B Истинное A→B A&B Связь понятий A&B v. B правильно отражает A A→B A&B B A→ Av. B A&B Высказывание Ложное Высказывание не соответствует реальной действительности свойства и отношения реальных вещей Высказывание Простое Составное содержание 6

A→B Av. B 1. 3. Умозаключение A&B A→B Av. B A&B Av. B A→B A&B v. B A Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение). Посылки – только истинные суждения. A→B A&B B A→ Av. B A&B содержание 8

A→B Av. B A&B A&B Av. B A→B A&B v. B A A→B A&B B A→ Av. B A&B 2. Алгебра высказываний служит для определения истинности или ложности составных высказываний. Высказывания обозначаются именами логических переменных (обозначаются прописными буквами латинского алфавита), которые могут принимать лишь два значения: «истина» (1) и «ложь» (0). Например: А = 1, В = 0 содержание 9
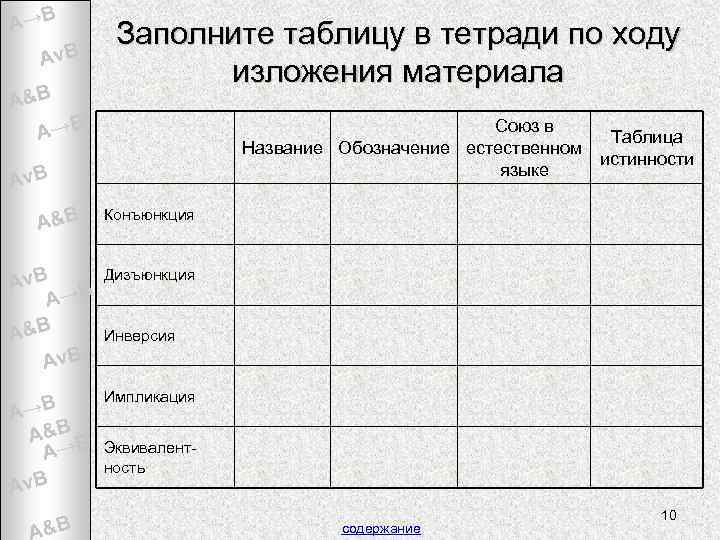
A→B Av. B A&B Заполните таблицу в тетради по ходу изложения материала A→B Союз в Таблица Название Обозначение естественном истинности языке Av. B A&B Конъюнкция Дизъюнкция Av. B A→B A&B Инверсия &B B A Av Импликация B A→ A&B B A→ Эквивалент- Av. B A&B ность содержание 10

A→B Av. B A&B Логические операции A→B Av. B A&B Av. B A→B A&B v. B A A→B A&B B A→ 2. 1. Логическое умножение (конъюнкция) 2. 2. Логическое сложение (дизъюнкция) 2. 3. Логическое отрицание (инверсия) 2. 4. Логическое следование (импликация) 2. 5. Логическое равенство (эквивалентность) Av. B A&B содержание 11

A→B Av. B A&B A&B Av. B A→B A&B v. B A A→B A&B B A→ Av. B A&B 2. 1. Логическое умножение (конъюнкция) Объединение двух (или нескольких) высказываний в одно с помощью союза «и» . Составное высказывание истинно только тогда, когда истины оба простых высказывания. Соответствует союзу И Обозначение & , ^ В языках программирования and Таблица истинности A B A&B 0 0 1 1 1 содержание Логические операции 12

A→B Av. B A&B 2. 2. Логическое сложение (дизъюнкция) Объединение двух (или нескольких) высказываний в одно с A→B помощью союза «или» . Составное высказывание истинно только тогда, когда истинно хотя бы одно из двух простых высказывания. Av. B A&B Соответствует союзу ИЛИ A&B Обозначение V В языках программирования or v. B A Таблица истинности A→B A&B v. B A A B Av. B A→B A&B B A→ 0 0 1 1 Av. B 1 1 1 A&B содержание Логические операции 13

A→B Av. B A&B A&B Av. B A→B A&B v. B A A→B A&B B A→ 2. 3. Логическое отрицание (инверсия) Присоединение частицы «не» к высказыванию. Инверсия делает истинное высказывание ложным и, наоборот. Соответствует союзу НЕ Обозначение Ā, ¬А В языках программирования not Таблица истинности A Ā 0 1 1 0 Av. B A&B содержание Логические операции 14

A→B Av. B A&B 2. 4. Логическое следование (импликация) Импликация образуется соединением двух высказываний в одно с помощью оборота речи «если…, то…» . A→B Импликация ложна только тогда, когда из истинного первого высказывания (предпосылки) следует ложный вывод (второе Av. B высказывание). A&B Соответствует обороту Если…, то… Обозначение А→В В языках программирования if … then … Av. B B A→ Таблица истинности A&B v. B A→B A&B B A→ Av. B A&B 0 0 1 0 1 1 1 содержание Логические операции 15
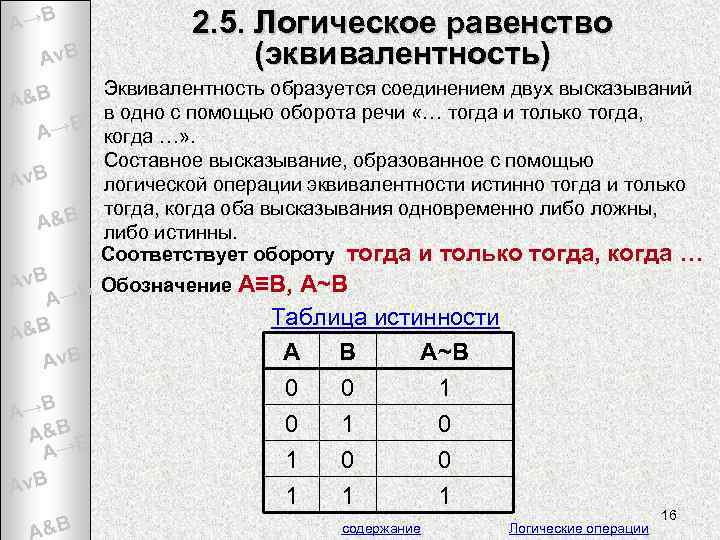
A→B Av. B 2. 5. Логическое равенство (эквивалентность) Эквивалентность образуется соединением двух высказываний в одно с помощью оборота речи «… тогда и только тогда, B A→ когда …» . Составное высказывание, образованное с помощью Av. B логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, A&B &B A либо истинны. Соответствует обороту тогда и только тогда, когда … Av. B Обозначение А≡В, А~B A→B Таблица истинности &B A B A& v. B A B А~B A A&B A→B A&B B A→ Av. B A&B 0 0 1 0 1 0 0 1 1 1 содержание Логические операции 16

A→B Av. B A&B A&B 3. Логические выражения и таблицы истинности Логическое выражение – формула, в которую входят логические переменные и знаки логических операций. Пример: Av. B A→B Порядок выполнения логических операций: 1. Действия в скобках. A&B B A& v. B 2. Инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность. A A→B A&B B A→ Av. B A&B Для логического выражения можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых высказываний. содержание 17

A→B Av. B A&B 4. Построение таблицы истинности 1. Определить количество строк в таблице по формуле 2 n, где n – количество логических Av. B переменных. A&B 2. Определить количество столбцов таблицы: A&B количество логических переменных + количество Av. B логических операций. A→B 3. Построить таблицу истинности, обозначить &B A B A& v. B столбцы, внести всевозможные наборы исходных A данных логических переменных. B A→ 4. Заполнить таблицу истинности, выполняя A&B B A→ базовые логические операции в необходимой Av. B последовательности. A→B A&B содержание 19

Построение таблицы истинности для A→B Av. B A&B A&B Av. B A→B A&B v. B A A→B A&B B A→ 1. Количество строк таблицы 22 = 4, т. к. в формуле две переменные A и B. 2. Количество столбцов: 2 переменные + 5 логических операций = 7. A 0 0 1 1 B 0 1 Av. B 0 1 1 1 0 0 1 1 0 Av. B A&B содержание 20

A→B Равносильные логические выражения Av. B A&B Равносильные логические выражения - это выражения, у B A→ которых последние столбцы таблиц истинности совпадают, обозначают “=“. Av. B Докажите равносильность выражений: A&B Таблица истинности для A&B Av. B A→B A&B v. B A A→B A&B B A→ Av. B A&B A 0 0 1 1 B 0 1 Av. B A 0 0 1 1 содержание B 0 1 21

A→B Av. B A&B A&B Av. B A→B A&B v. B A A→B A&B B A→ 5. Домашнее задание 1. Даны высказывания: A = «р делится на 5» В = «р – нечетное число» Найти множество значений р, при которых результат а) дизъюнкции, б) конъюнкции будет: 1) истинным; 2) ложным. Av. B A&B содержание 22

A→B Av. B A&B A&B Av. B A→B A&B v. B A A→B A&B B A→ Домашнее задание 2. Составьте и запишите истинные сложные высказывания из простых с использованием логических операций: 1) Неверно, что 10>Y>5 и Z<0. 2) Любое из чисел X, Y, Z положительно. 3. Составьте таблицу истинности для логического выражения: F = (X & ¬Y) v Z Av. B A&B содержание 23

A→B Проверь себя Av. B A&B A→B Av. B A&B Av. B A→B A&B v. B A A→B A&B B A→ • • • Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Av. B A&B содержание 24