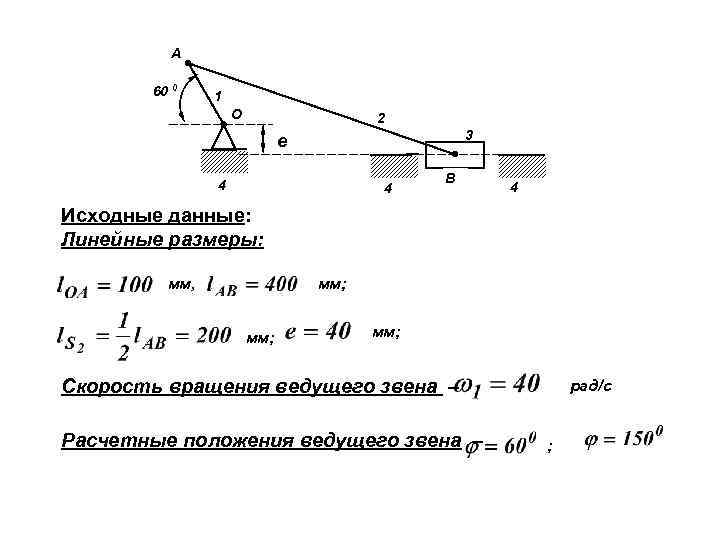
 А 60 0 1 О 2 3 е 4 4 В 4 Исходные данные: Линейные размеры: мм, мм; Скорость вращения ведущего звена – Расчетные положения ведущего звена – рад/с ;
А 60 0 1 О 2 3 е 4 4 В 4 Исходные данные: Линейные размеры: мм, мм; Скорость вращения ведущего звена – Расчетные положения ведущего звена – рад/с ;
 Массы звеньев – кг; кг. Момент инерции звена 2 относительно центра – кг·м 2. Усилие сопротивления движению ползуна – Н
Массы звеньев – кг; кг. Момент инерции звена 2 относительно центра – кг·м 2. Усилие сопротивления движению ползуна – Н
 Результаты кинематического расчета: Положение 600 Линейные ускорения : м/с2 ; м/с2 Угловое ускорение – рад/с2 (против часовой стрелки). Положение 1500 Линейные ускорения : м/с2 ; ; Угловое ускорение – рад/с2 (против часовой стрелки). м/с2
Результаты кинематического расчета: Положение 600 Линейные ускорения : м/с2 ; м/с2 Угловое ускорение – рад/с2 (против часовой стрелки). Положение 1500 Линейные ускорения : м/с2 ; ; Угловое ускорение – рад/с2 (против часовой стрелки). м/с2
 Силы инерции – Н Н Н Момент сил инерции (по часовой стрелке). Нм Веса звеньев : Н Н Н
Силы инерции – Н Н Н Момент сил инерции (по часовой стрелке). Нм Веса звеньев : Н Н Н
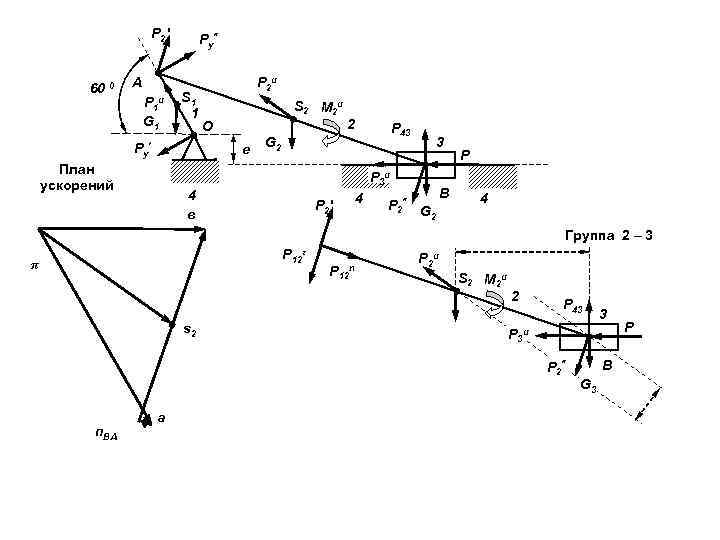 Р 2' 60 0 А Р 1 и G 1 Ру" S 1 1 Ру' P 2 и S 2 М 2 и О е План ускорений 2 P 43 G 2 3 P 3 и 4 в Р 2' 4 P 2" G 2 В P 4 Группа 2 – 3 Р 12τ π s 2 Р 12 n P 2 и S 2 М 2 и 2 P 43 P 3 и P 2" n. BA а 3 В G 3 P
Р 2' 60 0 А Р 1 и G 1 Ру" S 1 1 Ру' P 2 и S 2 М 2 и О е План ускорений 2 P 43 G 2 3 P 3 и 4 в Р 2' 4 P 2" G 2 В P 4 Группа 2 – 3 Р 12τ π s 2 Р 12 n P 2 и S 2 М 2 и 2 P 43 P 3 и P 2" n. BA а 3 В G 3 P
 В соответствии с методом кинетостатики векторная сумма всех сил, приложенных к рассматриваемому элементу механизма, включая и силы инерции равна нулю. Поэтому для группы 2 – 3 имеем В векторном уравнении имеются три неизвестных. Для возможности графического решения необходимо предварительно определить одно из таких неизвестных. Для этого используем уравнение равенство нулю моментов всех сил относительно точки В.
В соответствии с методом кинетостатики векторная сумма всех сил, приложенных к рассматриваемому элементу механизма, включая и силы инерции равна нулю. Поэтому для группы 2 – 3 имеем В векторном уравнении имеются три неизвестных. Для возможности графического решения необходимо предварительно определить одно из таких неизвестных. Для этого используем уравнение равенство нулю моментов всех сил относительно точки В.
 Плечи и находим из чертежа.
Плечи и находим из чертежа.
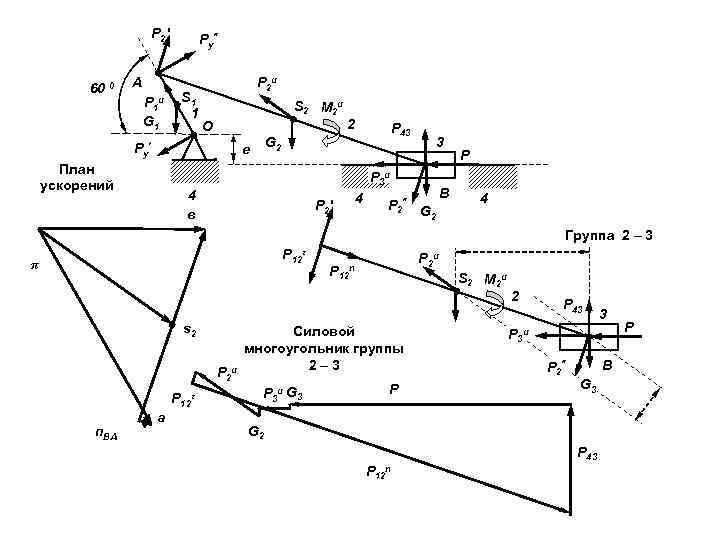 Р 2' 60 0 А Р 1 и G 1 Ру" S 1 1 P 2 и S 2 М 2 и О Ру' P 43 G 2 е План ускорений 2 3 P 3 и 4 в Р 2' 4 P 2" G 2 В P 4 Группа 2 – 3 Р 12τ π s 2 P 2 и Р 12τ n. BA а P 2 и Р 12 n S 2 М 2 и Силовой многоугольник группы 2– 3 P 3 и G 3 P 2 P 43 P 3 и P 2" В G 3 G 2 P 43 Р 12 n 3 P
Р 2' 60 0 А Р 1 и G 1 Ру" S 1 1 P 2 и S 2 М 2 и О Ру' P 43 G 2 е План ускорений 2 3 P 3 и 4 в Р 2' 4 P 2" G 2 В P 4 Группа 2 – 3 Р 12τ π s 2 P 2 и Р 12τ n. BA а P 2 и Р 12 n S 2 М 2 и Силовой многоугольник группы 2– 3 P 3 и G 3 P 2 P 43 P 3 и P 2" В G 3 G 2 P 43 Р 12 n 3 P
 Из векторного многоугольника находим длину отрезков: С учетом масштаба величина искомых усилий составляет:
Из векторного многоугольника находим длину отрезков: С учетом масштаба величина искомых усилий составляет:
 Рассмотрим отдельно равновесия звена 2 с учетом сил инерции и давления в шарнире В от звена 3. Уравнение равновесия в векторной форме будет следующим Построив векторный многоугольник, можно найти величину давления в шарнире В.
Рассмотрим отдельно равновесия звена 2 с учетом сил инерции и давления в шарнире В от звена 3. Уравнение равновесия в векторной форме будет следующим Построив векторный многоугольник, можно найти величину давления в шарнире В.
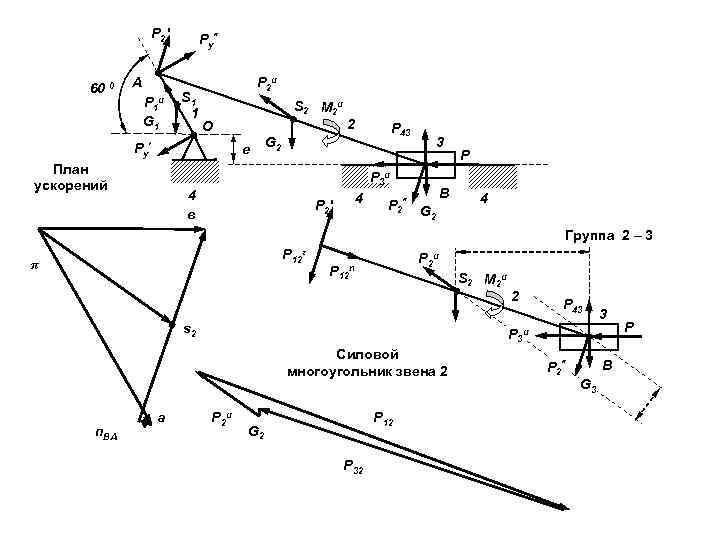 Р 2' 60 0 А Р 1 и G 1 Ру" S 1 1 P 2 и S 2 М 2 и О Ру' е План ускорений 2 P 43 G 2 3 P 3 и 4 в 4 Р 2' P 2" G 2 В P 4 Группа 2 – 3 Р 12τ π P 2 и Р 12 n S 2 М 2 и s 2 n. BA P 43 3 P 3 и Силовой многоугольник звена 2 P 2 и Р 12 G 2 Р 32 P 2" В G 3 P
Р 2' 60 0 А Р 1 и G 1 Ру" S 1 1 P 2 и S 2 М 2 и О Ру' е План ускорений 2 P 43 G 2 3 P 3 и 4 в 4 Р 2' P 2" G 2 В P 4 Группа 2 – 3 Р 12τ π P 2 и Р 12 n S 2 М 2 и s 2 n. BA P 43 3 P 3 и Силовой многоугольник звена 2 P 2 и Р 12 G 2 Р 32 P 2" В G 3 P
 Длина отрезка , соответствующая величине вектора давления в шарнире В, равна Величина усилия с учетом масштаба равна
Длина отрезка , соответствующая величине вектора давления в шарнире В, равна Величина усилия с учетом масштаба равна
 Р 2' 60 0 А Р 1 и G 1 Ру" S 1 1 Ру' P 2 и S 2 М 2 и О е План ускорений 2 P 43 G 2 3 P 3 и 4 в 4 P 2" G 2 В P 4 Ру" Р 21 π 60 0 s 2 А Р 1 и G 1 S 1 1 Ру' 4 n. BA а О
Р 2' 60 0 А Р 1 и G 1 Ру" S 1 1 Ру' P 2 и S 2 М 2 и О е План ускорений 2 P 43 G 2 3 P 3 и 4 в 4 P 2" G 2 В P 4 Ру" Р 21 π 60 0 s 2 А Р 1 и G 1 S 1 1 Ру' 4 n. BA а О
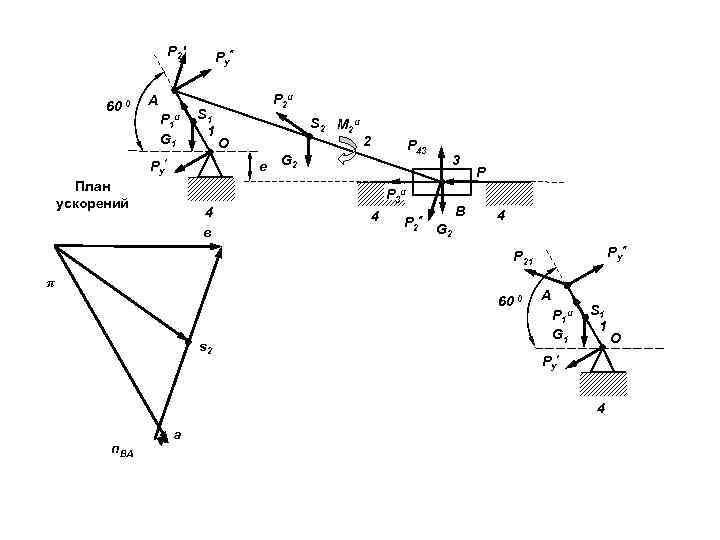
 Составляем уравнение моментов относительно точки О по методу кинетостатики. Величины плеч сил в расчетном уравнении берем с чертежа группы [ 4 – 1 ]. Удерживающий момент составит
Составляем уравнение моментов относительно точки О по методу кинетостатики. Величины плеч сил в расчетном уравнении берем с чертежа группы [ 4 – 1 ]. Удерживающий момент составит
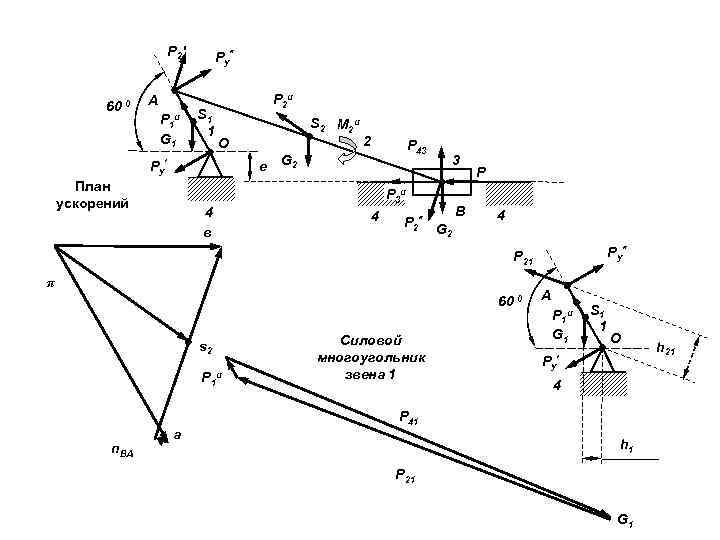
 Определим усилие в шарнире О из условия динамического равновесия звена 1. Строим векторный многоугольник. Размеры отрезков, соответствующие в масштабе величине векторов, будут равны: Отрезок, соответствующий величине вектора Р 41 , равен Величина вектора Р 41 с учетом масштаба равна
Определим усилие в шарнире О из условия динамического равновесия звена 1. Строим векторный многоугольник. Размеры отрезков, соответствующие в масштабе величине векторов, будут равны: Отрезок, соответствующий величине вектора Р 41 , равен Величина вектора Р 41 с учетом масштаба равна
 Р 2' 60 0 А Р 1 и G 1 Ру" S 1 1 P 2 и S 2 М 2 и О Ру' е План ускорений 2 P 43 G 2 3 P 3 и 4 в 4 P 2" G 2 В P 4 Ру" Р 21 π 60 0 s 2 Р 1 и n. BA а Силовой многоугольник звена 1 А Р 1 и G 1 S 1 1 О Ру' 4 Р 41 h 1 Р 21 G 1 h 21
Р 2' 60 0 А Р 1 и G 1 Ру" S 1 1 P 2 и S 2 М 2 и О Ру' е План ускорений 2 P 43 G 2 3 P 3 и 4 в 4 P 2" G 2 В P 4 Ру" Р 21 π 60 0 s 2 Р 1 и n. BA а Силовой многоугольник звена 1 А Р 1 и G 1 S 1 1 О Ру' 4 Р 41 h 1 Р 21 G 1 h 21
 Р 2' А 60 0 Р 1 и G 1 Ру" S 1 1 P 2 и S 2 М 2 и О Ру' е 2 P 43 G 2 3 P 3 и 4 P 2 и a 4 s 2 G 3 Ру" P 2" P 3 и G 2 Р 2' P в Р 1 и h 2" G 1 Ру' h 1 p h 2 и P 2" G 3 В P 4 План скоростей (перевернутый)
Р 2' А 60 0 Р 1 и G 1 Ру" S 1 1 P 2 и S 2 М 2 и О Ру' е 2 P 43 G 2 3 P 3 и 4 P 2 и a 4 s 2 G 3 Ру" P 2" P 3 и G 2 Р 2' P в Р 1 и h 2" G 1 Ру' h 1 p h 2 и P 2" G 3 В P 4 План скоростей (перевернутый)
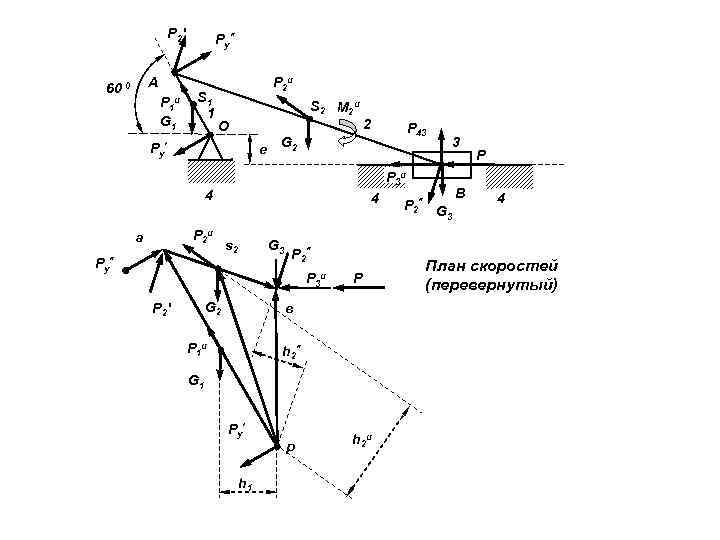
 Вычерчиваем кинематическую схему механизма с учетом всех сил, включая силы инерции. Вычерчиваем план скоростей, повернутый на 90 0, и в соответствующие точки переносим все силы Записываем уравнение динамического равновесия моментов всех сил относительно полюса « р » .
Вычерчиваем кинематическую схему механизма с учетом всех сил, включая силы инерции. Вычерчиваем план скоростей, повернутый на 90 0, и в соответствующие точки переносим все силы Записываем уравнение динамического равновесия моментов всех сил относительно полюса « р » .
 Величины плеч берем с чертежа
Величины плеч берем с чертежа
 Удерживающий момент равен Ошибка
Удерживающий момент равен Ошибка


