929 Точка А лежит на положительной полуоси

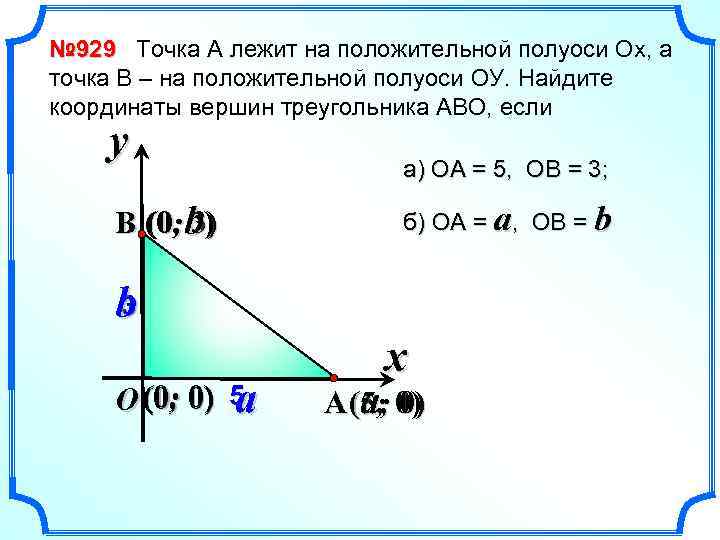№ 929 Точка А лежит на положительной полуоси Ох, а точка В – на положительной полуоси ОУ. Найдите координаты вершин треугольника АВО, если y B (0; b) 3) а) ОА = 5, ОВ = 3; б) ОА = a, ОВ = b 3 b O (0; 0) 5 a x A (5; 0) a; 0)

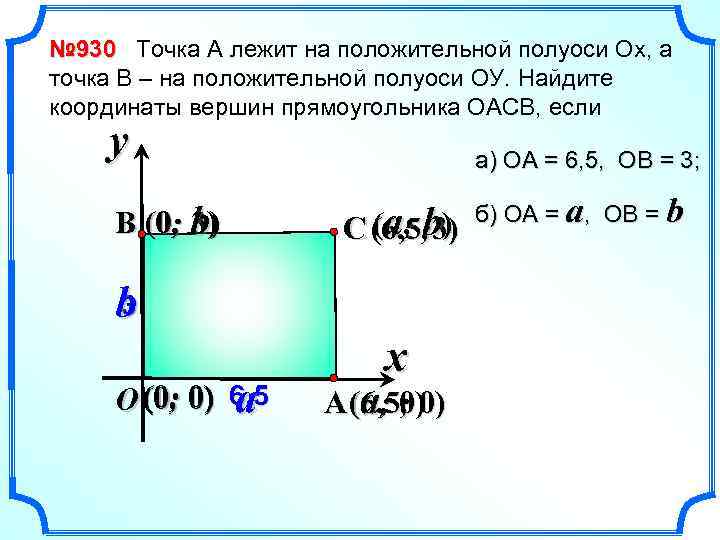№ 930 Точка А лежит на положительной полуоси Ох, а точка В – на положительной полуоси ОУ. Найдите координаты вершин прямоугольника ОАСВ, если y B (0; b) 3) а) ОА = 6, 5, ОВ = 3; a; b) C (6, 5; 3) 3 b O (0; 0) 6, 5 a x A (a; 0) 6, 5; 0) б) ОА = a, ОВ = b

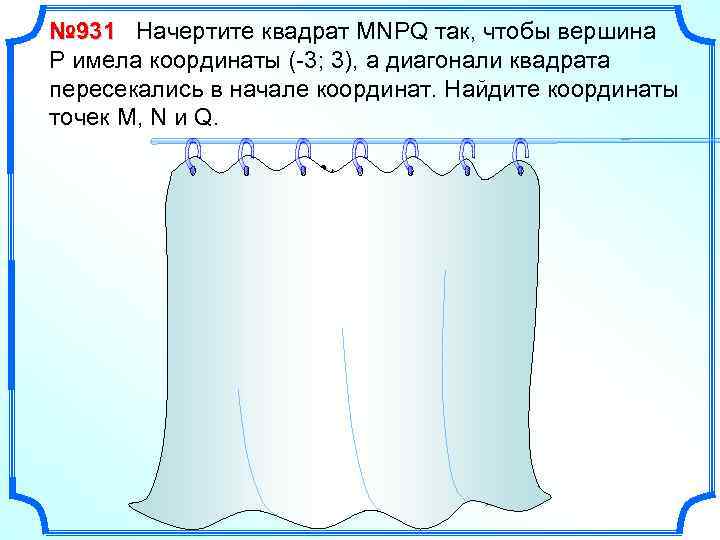№ 931 Начертите квадрат MNPQ так, чтобы вершина Р имела координаты (-3; 3), а диагонали квадрата пересекались в начале координат. Найдите координаты точек M, N и Q. y P(-3; 3) Q (3; 3) O N(-3; -3) x M(3; -3)

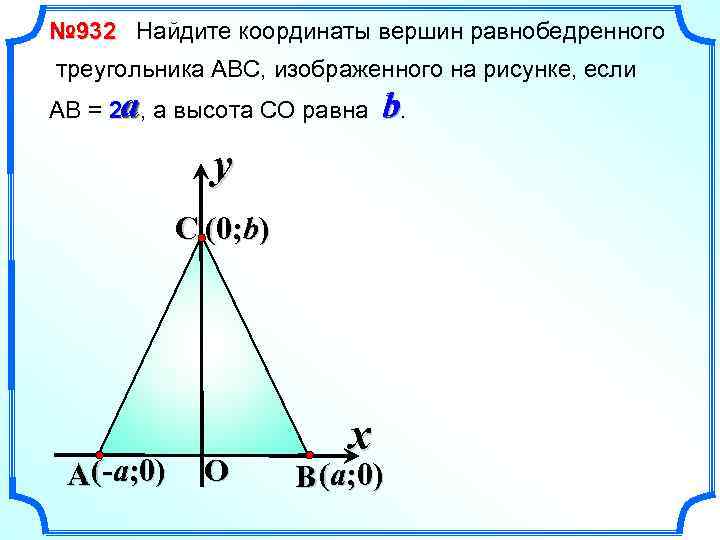№ 932 Найдите координаты вершин равнобедренного треугольника АВС, изображенного на рисунке, если АВ = 2 a, а высота СО равна b. y C (0; b) A(-a; 0) O x B (a; 0)

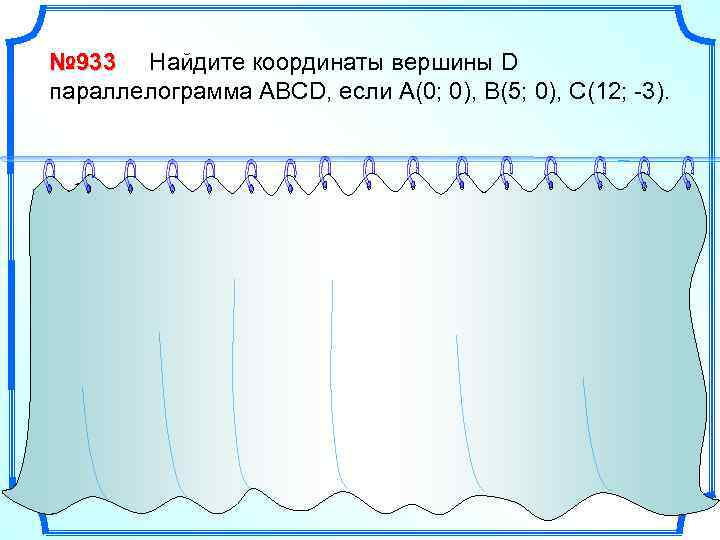№ 933 Найдите координаты вершины D параллелограмма АВСD, если А(0; 0), В(5; 0), С(12; -3). y A (0; 0) 5 x B(5; 0) D (7; -3) C (12; -3) -5

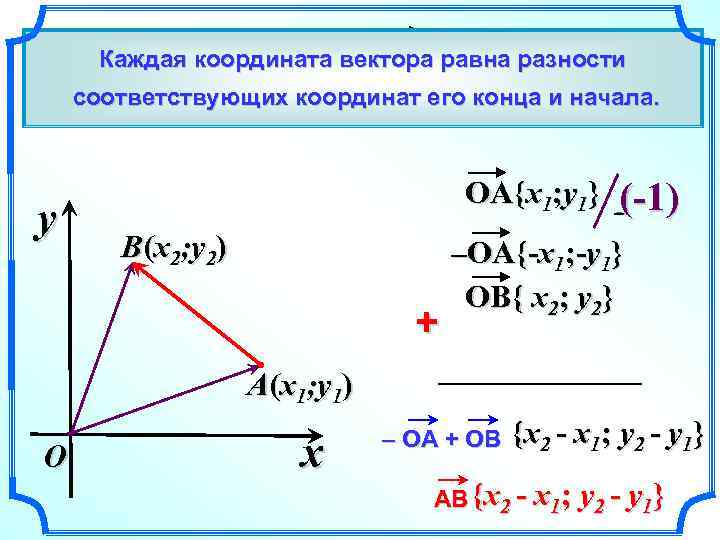Выразим координаты вектора АВ через координаты его Каждая координата вектора равна разности начала А и конца В. соответствующих координат его конца и начала. AB = AO + OВ = – OA + OВ y OA{x 1; y 1} B (x 2; y 2) + (-1) –OA{-x 1; -y 1} OB{ x 2; y 2} A (x 1; y 1) O x – OA + OВ {x 2 - x 1; y 2 - y 1} AB {x 2 - x 1; y 2 - y 1}

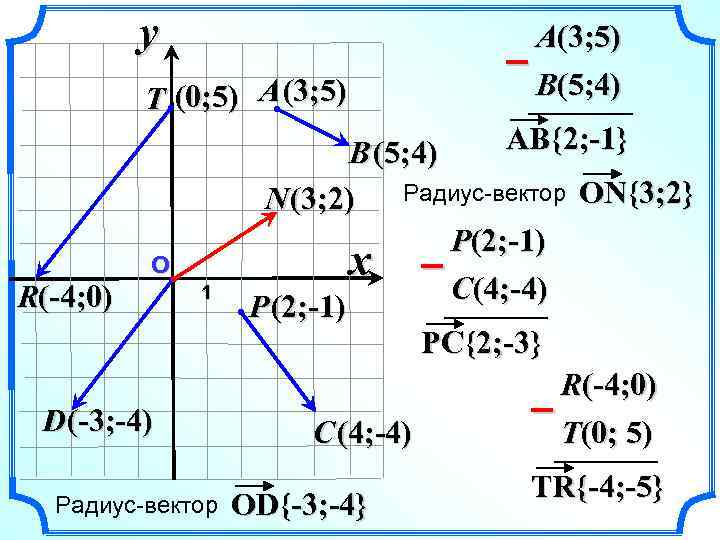y T (0; 5) A (3; 5) R(-4; 0) О 1 D(-3; -4) Радиус-вектор A(3; 5) – B(5; 4) AB{2; -1} B (5; 4) Радиус-вектор ON{3; 2} N (3; 2) P(2; -1) x – C(4; -4) P (2; -1) PC{2; -3} R(-4; 0) – C (4; -4) T(0; 5) OD{-3; -4} TR{-4; -5}

Найдите координаты векторов M(-2; 7) – R(2; 7); M(-2; 7); RM RM{-4; 0} P(-5; 1); D(-5; 7); PD D(-5; 7) – P(-5; 1) PD{ 0; 6} N(0; 5) – R(-3; 0) RN{3; 5} A(0; 3) – B(-4; 0) BA{4; 3} B(-2; 0) – A(-2; 7) AB{0; -7} T(-2; -7) – R(-7; 7) RT{5; -14} R(-3; 0); N(0; 5); RN A(0; 3); B(-4; 0); BA A(-2; 7); B(-2; 0); AB R(-7; 7); T(-2; -7); RT

Найти координаты векторов. R(2; 7); M(-2; 7); RM{ } P(-5; 1); D(-5; 7); PD { } R(-3; 0); N(0; 5); RN { } A(0; 3); B(-4; 0); BA { } A(-2; 7); B(-2; 0); AB { } R(-7; 7); T(-2; -7); RT { } Вводите ответы в текстовые поля, не делая пробелов

Обратные задачи. Дано: AB{2; -1}, Найти: – B(5; 4) Найти: A(x; y) B(5; 4) A(x; y) x=3 A(2; -4) B(x; y) – B(x; y) A(2; -4) AB{2; -1} 5–x=2 Дано: AB{2; -1}, 4 – y = -1 y=5 x– 2=2 x=4 y + 4= -1 y = -5

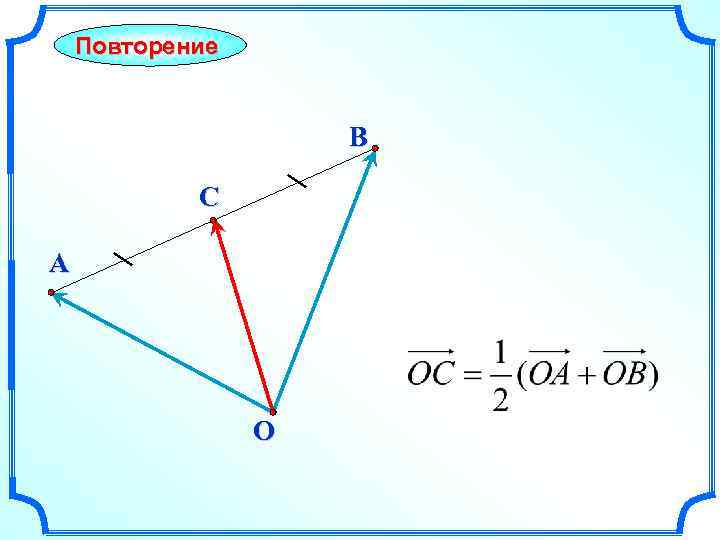Повторение B C A O

Координаты середины отрезка + y OB{x 2; y 2} OA+OB {x 1+x 2; y 1+y 2} B(x 2; y 2) C (x 0; y 0) 1 2 x : 2 x 1+x 2 y 1+y 2 (OA+OB) { ; } 2 2 2 A(x 1; y 1) О OA{x 1; y 1} 2 x 1+x 2 y 1+y 2 OC { ; } 2 2 x 0= 2 x 1+x 2 2 ; y 0 = 2 y 1+y 2 2

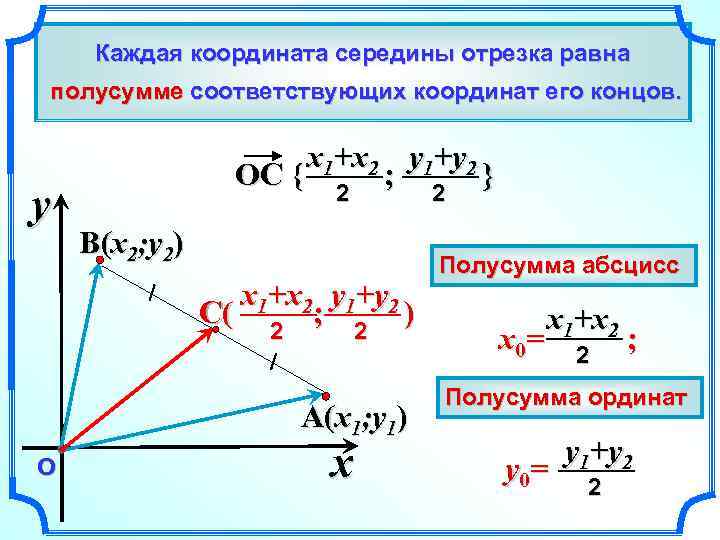Каждая координата середины отрезка равна полусумме соответствующих координат его концов. y x 1+x 2 y 1+y 2 OC { ; } 2 2 B(x 2; y 2) x 1+x 2 y 1+y 2 C( ; ) 2 2 A(x 1; y 1) О x Полусумма абсцисс x 0= x 1+x 2 2 ; Полусумма ординат y 0= y 1+y 2 2

y Полусумма абсцисс T (0; 5) A (3; 5) C B(5; 4) N (3; 2) S R(-4; 0) 1 Q D(-3; -4) x F О P (2; -1) V C (4; -4) x 0= x 1+x 2 2 ; Полусумма ординат y 0= y 1+y 2 2 3 +0 3 +5 5 +0 +4 2 +4 ; ; y = 2 0+(-4) -1+(-4) x 00= 0+(-3) y 00= 2 ; ; x = 0+(-4) y = 5+0 = 2 x 00= 2 ; ; ; 0 y 0= 2 2 x x 0 = 2 2 y 0 = 22 2 C(4; 4, 5) F(1, 5; 1) V(3; -2, 5) Q(-1, 5; -2) S(-2; 2, 5)

Найдите координаты cередин отрезков R(2; 7); M(-2; 7); C P(-5; 1); D(-5; 7); C 2+(-2) 7 + 7 ( ; ); 2 2 ( -5+(-5) ; 1 + 7 ); 2 2 R(-3; 0); N(0; 5); C -3 + 0 ( 2 A(0; -6); B(-4; 2); ( 0+(-4) ; -6+2 ); C(-2; -2) C 2 2 A(7; 7); B(-2; 0); C 7+(-2) ( 2 0+5 ; ); 2 7+0 ; ); 2 C(0; 7) C(-1, 5; 2, 5) C(-5; 4) C(2, 5; 3, 5) R(-7; 4); T(-2; -7); C ( -7+(-2) ; 4+(-7)); C(-4, 5; -1, 5) 2 2

Найти координаты середин отрезков. R(2; 7); M(-2; 7); C( ) P(-5; 1); D(-5; 7); C( ) R(-3; 0); N(0; 5); C( ) A(0; -6); B(-4; 2); C( ) A(7; 7); B(-2; 0); C( ) R(-7; 4); T(-2; -7); C( ) Вводите ответы в текстовые поля, не делая пробелов

Обратная задача. Дано: A(5; 4); C(-3; 2) – середина отрезка AB Найти: x 0= B(x; y) x 1+x 2 2 y 0= ; 5+x -3= 2 ; A(5; 4) 2 C(-3; 2) y 1+y 2 B(x; y) 2 4+y 2= 2 ; – 6=5+x 4=4+y x = – 11 y=0 2 B(-11; 0)

Вычисление длины вектора по его координатам OA 2=OA 12 + AA 12 y OA 2= x 2 + y 2 OA OA= a{x; y} A (x; y) A 2 y О a OA = x 2 + y 2 = x A 1 x =

Расстояние между двумя точками y d M 2(x 2; y 2) – M 1(x 1; y 1) M 1 M 2 {x 2–x 1; y 2–y 1} M 1(x 1; y 1) O a x x 2 + y 2 = M 1 M 2 = (x 2–x 1)2+(y 2–y 1)2 d= (x 2–x 1)2+(y 2–y 1)2

№ 940 Найдите расстояние между точками A(2; 7) и B(-2; 7) 2 способ 1 способ a 1) – = x 2 + y 2 B(-2; 7) A( 2; 7) M 1 M 2 = (x 2–x 1)2+(y 2–y 1)2 AB = (– 2– 2)2+(7– 7)2 AB{-4; 0} 2) AB = (-4)2 + 02 = 16 = 4

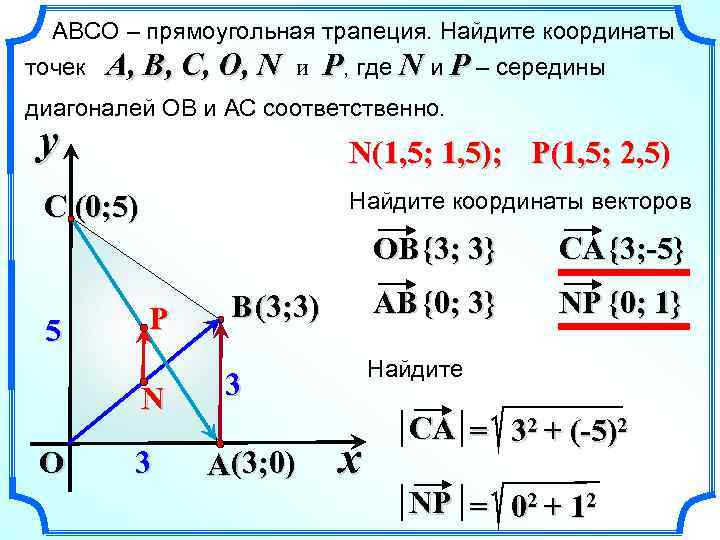ABCО – прямоугольная трапеция. Найдите координаты точек A , B , C , O, N и P, где N и P – середины диагоналей OB и AC соответственно. y N(1, 5; 1, 5); P(1, 5; 2, 5) C (0; 5) Найдите координаты векторов OB {3; 3} 5 P N O 3 CA {3; -5} B (3; 3) AB {0; 3} NP {0; 1} 3 Найдите A(3; 0) x CA = 32 + (-5)2 NP = 02 + 12

ABCО – прямоугольная трапеция. Найдите координаты точек A , B , C , O, N и P, где N и P – середины диагоналей AC и OB соответственно. y N(-1; 2); P(-4; 2) Найдите координаты векторов B (-8; 4) 8 A (0; 4) N 2 C(-2; 0) 4 P O OA{0; 4} CA {2; 4} AB {-8; 0} NP {-3; 0} Найдите x CA = 22 + 42 NP = (-3)2 + 02