c0d469eb6c7ec2e3be4e2d99751d7ccd.ppt
- Количество слайдов: 95

9 Machine Learning: Symbol-based 9. 0 Introduction 9. 5 Knowledge and Learning 9. 1 A Framework for Symbol-based Learning 9. 6 Unsupervised Learning 9. 7 Reinforcement Learning 9. 8 Epilogue and References 9. 9 Exercises 9. 2 Version Space Search 9. 3 The ID 3 Decision Tree Induction Algorithm 9. 4 Inductive Bias and Learnability Additional source used in preparing the slides: Jean-Claude Latombe’s CS 121 (Introduction to Artificial Intelligence) lecture notes, http: //robotics. stanford. edu/~latombe/cs 121/2003/home. htm (version spaces, decision trees) Tom Mitchell’s machine learning notes (explanation based learning) 1

Chapter Objectives • Learn about several “paradigms” of symbolbased learning • Learn about the issues in implementing and using learning algorithms • The agent model: can learn, i. e. , can use prior experience to perform better in the future 2
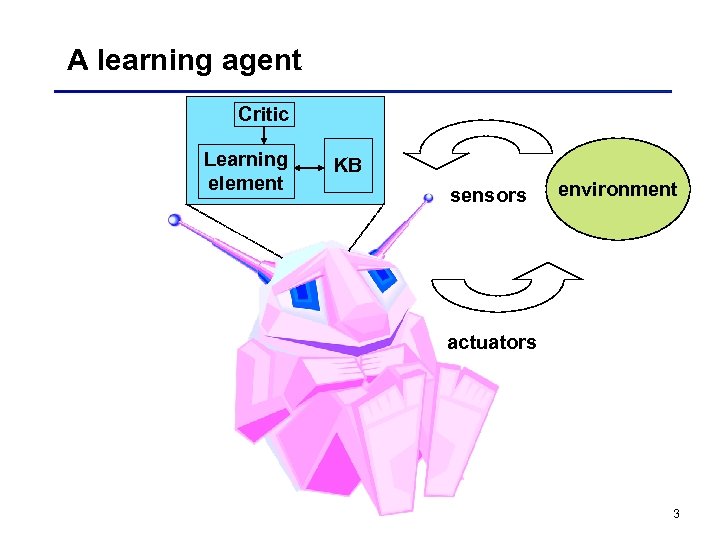
A learning agent Critic Learning element KB sensors environment actuators 3
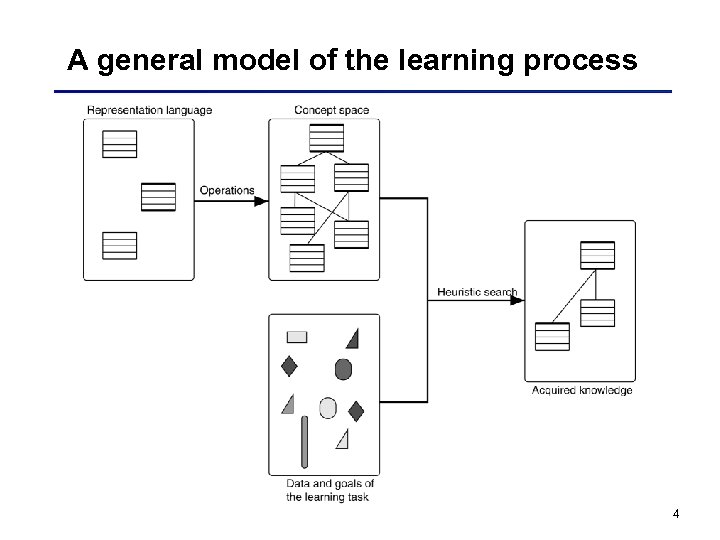
A general model of the learning process 4

A learning game with playing cards I would like to show what a full house is. I give you examples which are/are not full houses: 6 6 6 9 9 is a full house 6 6 9 house is not a full 3 3 3 6 6 is a full house 1 1 1 6 6 is a full house Q Q Q 6 6 is a full house 1 2 3 4 5 house is not a full 1 1 1 4 5 is not a full 5

A learning game with playing cards If you haven’t guessed already, a full house is three of a kind a pair of another kind. 6 6 6 9 9 is a full house 6 6 9 house is not a full 3 3 3 6 6 is a full house 1 1 1 6 6 is a full house Q Q Q 6 6 is a full house 1 2 3 4 5 house is not a full 1 1 1 4 5 is not a full 6

Intuitively, I’m asking you to describe a set. This set is the concept I want you to learn. This is called inductive learning, i. e. , learning a generalization from a set of examples. Concept learning is a typical inductive learning problem: given examples of some concept, such as “cat, ” “soybean disease, ” or “good stock investment, ” we attempt to infer a definition that will allow the learner to correctly recognize future instances of that concept. 7

Supervised learning This is called supervised learning because we assume that there is a teacher who classified the training data: the learner is told whether an instance is a positive or negative example of a target concept. 8

Supervised learning? This definition might seem counter intuitive. If the teacher knows the concept, why doesn’t s/he tell us directly and save us all the work? The teacher only knows the classification, the learner has to find out what the classification is. Imagine an online store: there is a lot of data concerning whether a customer returns to the store. The information is there in terms of attributes and whether they come back or not. However, it is up to the learning system to characterize the concept, e. g, If a customer bought more than 4 books, s/he will return. If a customer spent more than $50, s/he will return. 9
![Rewarded card example • Deck of cards, with each card designated by [r, s], Rewarded card example • Deck of cards, with each card designated by [r, s],](https://present5.com/presentation/c0d469eb6c7ec2e3be4e2d99751d7ccd/image-10.jpg)
Rewarded card example • Deck of cards, with each card designated by [r, s], its rank and suit, and some cards “rewarded” • Background knowledge in the KB: ((r=1) … (r=10)) NUM (r) ((r=J) (r=Q) (r=K)) FACE (r) ((s=S) (s=C)) BLACK (s) ((s=D) (s=H)) RED (s) • Training set: REWARD([4, C]) REWARD([7, C]) REWARD([2, S]) REWARD([5, H]) REWARD([J, S]) 10
![Rewarded card example Training set: REWARD([4, C]) REWARD([7, C]) REWARD([2, S]) REWARD([5, H]) REWARD([J, Rewarded card example Training set: REWARD([4, C]) REWARD([7, C]) REWARD([2, S]) REWARD([5, H]) REWARD([J,](https://present5.com/presentation/c0d469eb6c7ec2e3be4e2d99751d7ccd/image-11.jpg)
Rewarded card example Training set: REWARD([4, C]) REWARD([7, C]) REWARD([2, S]) REWARD([5, H]) REWARD([J, S]) Card 4 7 2 5 J In the target set? yes yes no no Possible inductive hypothesis, h, : h = (NUM (r) BLACK (s) REWARD([r, s]) 11

Learning a predicate • Set E of objects (e. g. , cards, drinking cups, writing instruments) • Goal predicate CONCEPT (X), where X is an object in E, that takes the value True or False (e. g. , REWARD, MUG, PENCIL, BALL) • Observable predicates A(X), B(X), … (e. g. , NUM, RED, HAS-HANDLE, HAS-ERASER) • Training set: values of CONCEPT for some combinations of values of the observable predicates • Find a representation of CONCEPT of the form CONCEPT(X) A(X) ( B(X) C(X) ) 12

How can we do this? • Go with the most general hypothesis possible: “any card is a rewarded card” This will cover all the positive examples, but will not be able to eliminate any negative examples. • Go with the most specific hypothesis possible: “the rewarded cards are 4 , 7 , 2 ” This will correctly sort all the examples in the training set, but it is overly specific, will not be sort any new examples. • But the above two are good starting points. 13

Version space algorithm • What we want to do is start with the most general and specific hypotheses, and when we see a positive example, we minimally generalize the most specific hypotheses when we see a negative example, we minimally specialize the most general hypothesis • When the most general hypothesis and the most specific hypothesis are the same, the algorithm has converged, this is the target concept 14
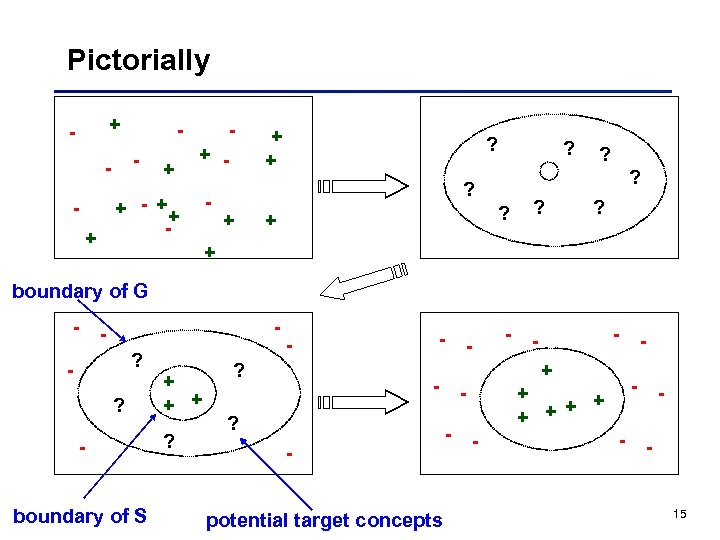
Pictorially + - - - + + - ++ + - + + ? ? - + boundary of G - - ? ? - boundary of S + + + ? - potential target concepts + - ? - - - + + + - - - 15

Hypothesis space • When we shrink G, or enlarge S, we are essentially conducting a search in the hypothesis space • A hypothesis is any sentence h of the form CONCEPT(X) A(X) ( B(X) C(X) ) where, the right hand side is built with observable predicates • The set of all hypotheses is called the hypothesis space, or H • A hypothesis h agrees with an example if it gives the correct value of CONCEPT 16

Size of the hypothesis space • n observable predicates • 2^n entries in the truth table • A hypothesis is any subset of observable predicates with the associated truth tables: so there are 2^(2^n) hypotheses to choose from: BIG! 2 n 2 • n=6 2 ^ 64 = 1. 8 x 10 ^ 19 BIG! • Generate-and-test won’t work. 17

Simplified Representation for the card problem For simplicity, we represent a concept by rs, with: • r = a, n, f, 1, …, 10, j, q, k • s = a, b, r, , For example: • n represents: NUM(r) (s= ) REWARD([r, s]) • aa represents: ANY-RANK(r) ANY-SUIT(s) REWARD([r, s]) 18

Extension of an hypothesis The extension of an hypothesis h is the set of objects that verifies h. For instance, the extension of f is: {j , q , k }, and the extension of aa is the set of all cards. 19

More general/specific relation Let h 1 and h 2 be two hypotheses in H h 1 is more general than h 2 iff the extension of h 1 is a proper superset of the extension of h 2 For instance, aa is more general than f , f is more general than q , fr and nr are not comparable 20

More general/specific relation (cont’d) The inverse of the “more general” relation is the “more specific” relation The “more general” relation defines a partial ordering on the hypotheses in H 21
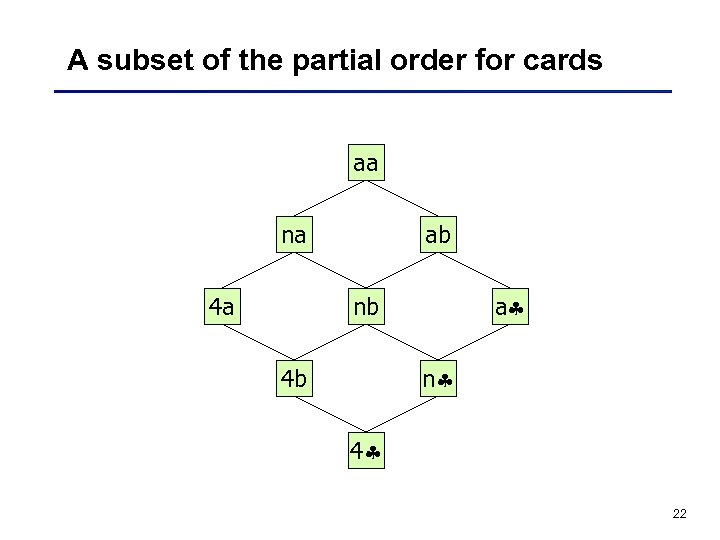
A subset of the partial order for cards aa na 4 a ab a nb n 4 b 4 22

G-Boundary / S-Boundary of V An hypothesis in V is most general iff no hypothesis in V is more general G-boundary G of V: Set of most general hypotheses in V An hypothesis in V is most specific iff no hypothesis in V is more general S-boundary S of V: Set of most specific hypotheses in V 23
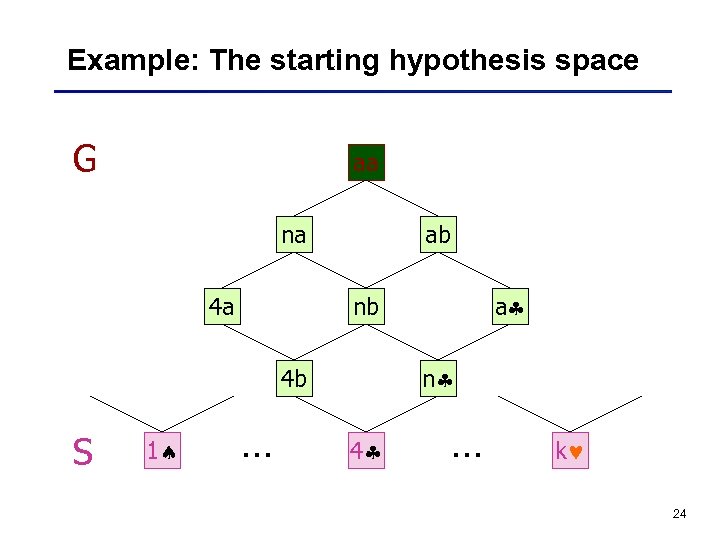
Example: The starting hypothesis space G aa na 4 a ab n 4 b S 1 a nb … 4 … k 24
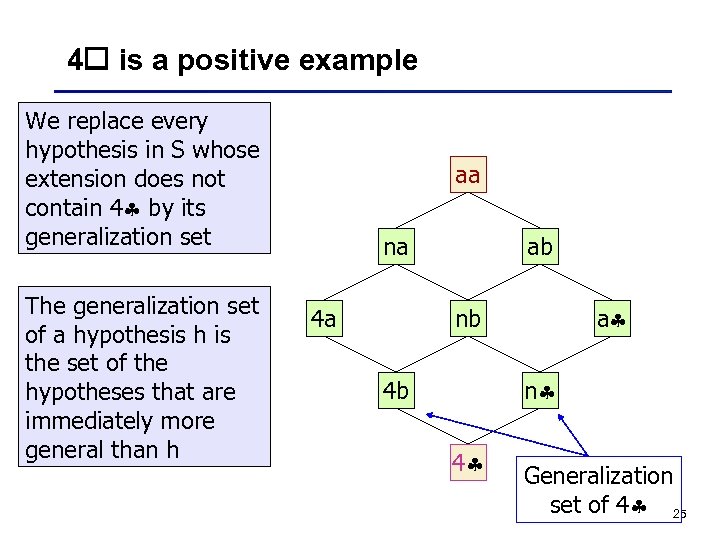
4 is a positive example We replace every hypothesis in S whose extension does not contain 4 by its generalization set The generalization set of a hypothesis h is the set of the hypotheses that are immediately more general than h aa na 4 a ab a nb n 4 b 4 Generalization set of 4 25

7 is the next positive example Minimally generalize the most specific hypothesis set We replace every hypothesis in S whose extension does not contain 7 by its generalization set aa na 4 a ab a nb n 4 b 4 26
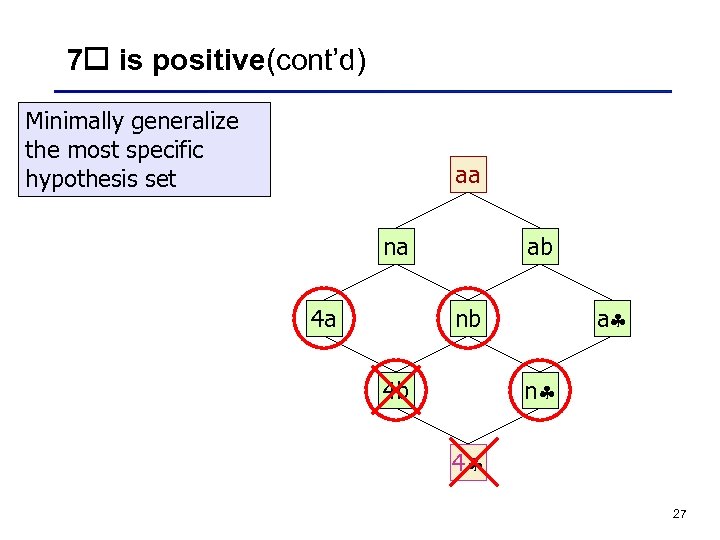
7 is positive(cont’d) Minimally generalize the most specific hypothesis set aa na 4 a ab a nb n 4 b 4 27
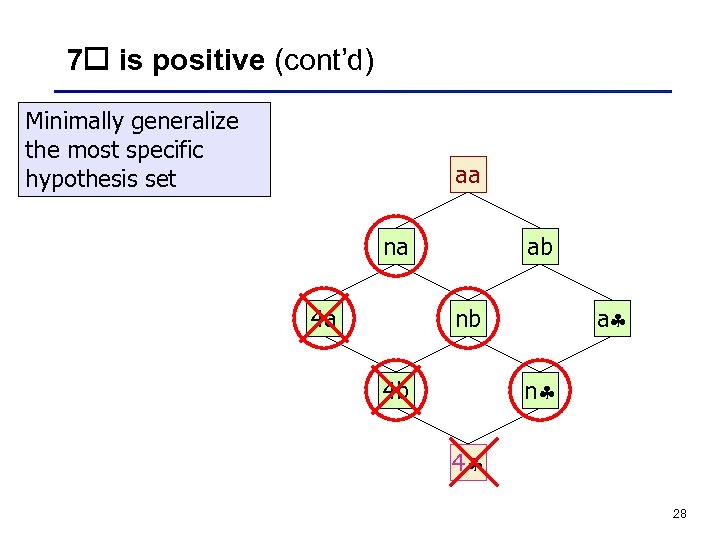
7 is positive (cont’d) Minimally generalize the most specific hypothesis set aa na 4 a ab a nb n 4 b 4 28
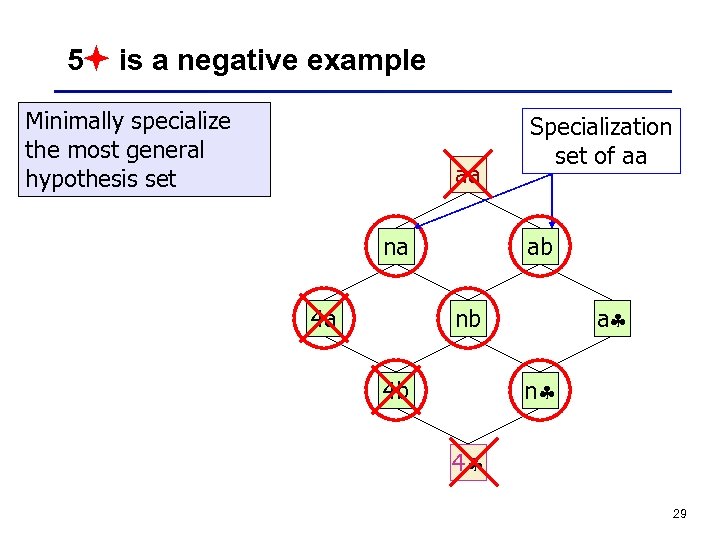
5 is a negative example Minimally specialize the most general hypothesis set aa na 4 a Specialization set of aa ab a nb n 4 b 4 29
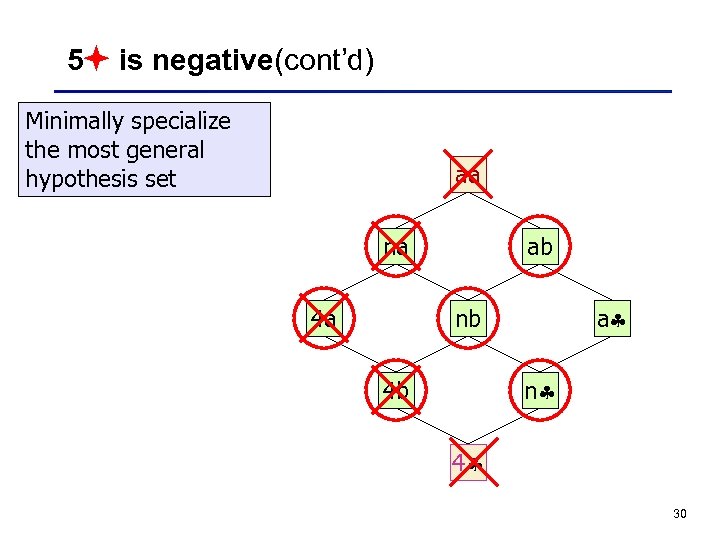
5 is negative(cont’d) Minimally specialize the most general hypothesis set aa na 4 a ab a nb n 4 b 4 30

After 3 examples (2 positive, 1 negative) G and S, and all hypotheses in between form exactly the version space ab a nb 1. If an hypothesis between G and S disagreed with an example x, then an hypothesis G or S would also disagree with x, hence would have been removed n 31

After 3 examples (2 positive, 1 negative) G and S, and all hypotheses in between form exactly the version space ab nb a 2. If there were an hypothesis n not in this set which agreed with all examples, then it would have to be either no more specific than any member of G – but then it would be in G – or no more general than some member of S – but then it would be in S 32
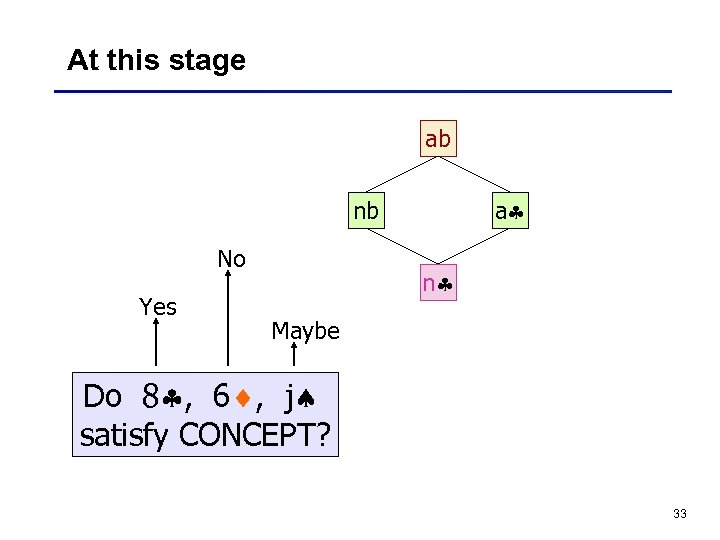
At this stage ab a nb No Yes n Maybe Do 8 , 6 , j satisfy CONCEPT? 33
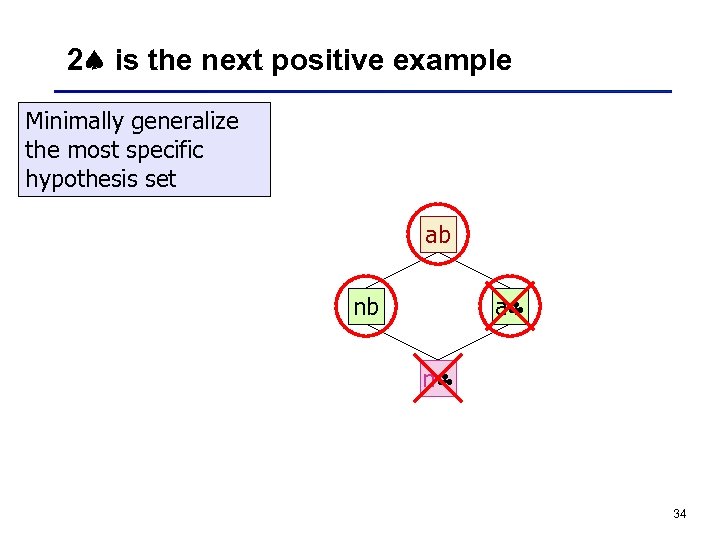
2 is the next positive example Minimally generalize the most specific hypothesis set ab a nb n 34

j is the next negative example Minimally specialize the most general hypothesis set ab nb 35
![Result + 4 7 2 – 5 j nb NUM(r) BLACK(s) REWARD([r, s]) 36 Result + 4 7 2 – 5 j nb NUM(r) BLACK(s) REWARD([r, s]) 36](https://present5.com/presentation/c0d469eb6c7ec2e3be4e2d99751d7ccd/image-36.jpg)
Result + 4 7 2 – 5 j nb NUM(r) BLACK(s) REWARD([r, s]) 36

The version space algorithm Begin Initialize S to the first positive training instance N is the set of all negative instances seen so far; For each example x If x is positive, then (G, S) POSITIVE-UPDATE(G, S, x) else (G, S) NEGATIVE-UPDATE(G, S, x) If G = S and both are singletons, then the algorithm has found a single concept that is consistent with all the data and the algorithm halts If G and S become empty, then there is no concept that covers all the positive instances and none of the negative instances End 37

The version space algorithm (cont’d) POSITIVE-UPDATE(G, S, x) Begin Delete all members of G that fail to match x For every s S, if s does not match x, replace s with its most specific generalizations that match x; Delete from S any hypothesis that is more general than some other hypothesis in S; Delete from S any hypothesis that is neither more specific than nor equal to a hypothesis in G; (different than the textbook) End; 38

The version space algorithm (cont’d) NEGATIVE-UPDATE(G, S, x) Begin Delete all members of S that match x For every g G, that matches x, replace g with its most general specializations that do not match x; Delete from G any hypothesis that is more specific than some other hypothesis in G; Delete from G any hypothesis that is neither more general nor equal to hypothesis in S; (different than the textbook) End; 39

Comments on Version Space Learning (VSL) • It is a bi-directional search. One direction is specific to general and is driven by positive instances. The other direction is general to specific and is driven by negative instances. • It is an incremental learning algorithm. The examples do not have to be given all at once (as opposed to learning decision trees. ) The version space is meaningful even before it converges. • The order of examples matters for the speed of convergence • As is, cannot tolerate noise (misclassified examples), the version space might collapse 40

Examples and near misses for the concept “arch” 41

More on generalization operators • Replacing constants with variables. For example, color (ball, red) generalizes to color (X, red) • Dropping conditions from a conjunctive expression. For example, shape (X, round) size (X, small) color (X, red) generalizes to shape (X, round) color (X, red) 42

More on generalization operators (cont’d) • Adding a disjunct to an expression. For example, shape (X, round) size (X, small) color (X, red) generalizes to shape (X, round) size (X, small) ( color (X, red) (color (X, blue) ) • Replacing a property with its parent in a class hierarchy. If we know that primary_color is a superclass of red, then color (X, red) generalizes to color (X, primary_color) 43

Another example • sizes = {large, small} • colors = {red, white, blue} • shapes = {sphere, brick, cube} • object (size, color, shape) • If the target concept is a “red ball, ” then size should not matter, color should be red, and shape should be sphere • If the target concept is “ball, ” then size or color should not matter, shape should be sphere. 44

A portion of the concept space 45

Learning the concept of a “red ball” G : { obj (X, Y, Z)} S: {} positive: obj (small, red, sphere) G: { obj (X, Y, Z)} S : { obj (small, red, sphere) } negative: obj (small, blue, sphere) G: { obj (large, Y, Z), obj (X, red, Z), obj (X, white, sphere) obj (X, Y, brick), obj (X, Y, cube) } S: { obj (small, red, sphere) } delete from G every hypothesis that is neither more general than nor equal to a hypothesis in S G: {obj (X, red, Z) } S: { obj (small, red, sphere) } 46

Learning the concept of a “red ball” (cont’d) G: { obj (X, red, Z) } S: { obj (small, red, sphere) } positive: obj (large, red, sphere) G: { obj (X, red, Z)} S : { obj (X, red, sphere) } negative: obj (large, red, cube) G: { obj (small, red, Z), obj (X, red, sphere), obj (X, red, brick)} S: { obj (X, red, sphere) } delete from G every hypothesis that is neither more general than nor equal to a hypothesis in S G: {obj (X, red, sphere) } S: { obj (X, red, sphere) } converged to a single concept 47

LEX: a program that learns heuristics • Learns heuristics for symbolic integration problems • Typical transformations used in performing integration include OP 1: r f(x) dx r f(x) dx OP 2: u dv uv - v du OP 3: 1 * f(x) OP 4: (f 1(x) + f 2(x)) dx f 1(x) dx + f 2(x) dx • A heuristic tells when an operator is particularly useful: If a problem state matches x transcendental(x) dx then apply OP 2 with bindings u=x dv = transcendental (x) dx 48
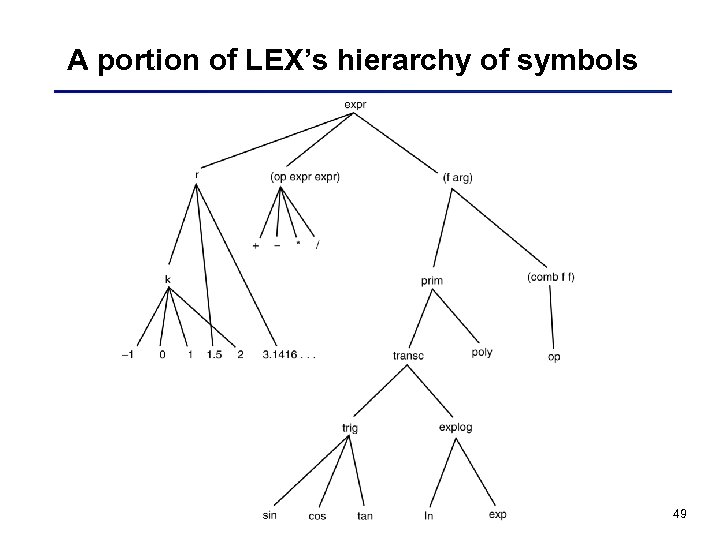
A portion of LEX’s hierarchy of symbols 49

The overall architecture • A generalizer that uses candidate elimination to find heuristics • A problem solver that produces positive and negative heuristics from a problem trace • A critic that produces positive and negative instances from a problem traces (the credit assignment problem) • A problem generator that produces new candidate problems 50

A version space for OP 2 (Mitchell et al. , 1983) 51

Comments on LEX • The evolving heuristics are not guaranteed to be admissible. The solution path found by the problem solver may not actually be a shortest path solution. • The problem generator is the least developed part of the program. • Empirical studies: before: 5 problems solved in an average of 200 steps train with 12 problems after: 5 problems solved in an average of 20 steps 52

More comments on VSL • Still lots of research going on • Uses breadth-first search which might be inefficient: · might need to use beam-search to prune hypotheses from G and S if they grow excessively · another alternative is to use inductive-bias and restrict the concept language • How to address the noise problem? Maintain several G and S sets. 53

Decision Trees • A decision tree allows a classification of an object by testing its values for certain properties • check out the example at: www. aiinc. ca/demos/whale. html • The learning problem is similar to concept learning using version spaces in the sense that we are trying to identify a class using the observable properties. • It is different in the sense that we are trying to learn a structure that determines class membership after a sequence of questions. This structure is a decision tree. 54

Reverse engineered decision tree of the whale watcher expert system see flukes? yes see dorsal fin? yes no size? vlg med blue blow whale forward? yes no sperm whale humpback whale no (see next page) yes size med? blows? 1 gray whale no Size? 2 lg right bowhead whale vsm narwhale 55

Reverse engineered decision tree of the whale watcher expert system (cont’d) see flukes? yes no (see previous page) yes see dorsal fin? no blow? no yes lg size? dorsal fin and blow visible at the same time? yes no sei whale fin whale sm dorsal fin tall and pointed? yes no killer whale northern bottlenose whale 56

What does the original data look like? 57

The search problem Given a table of observable properties, search for a decision tree that • correctly represents the data (assuming that the data is noise-free), and • is as small as possible. What does the search tree look like? 58
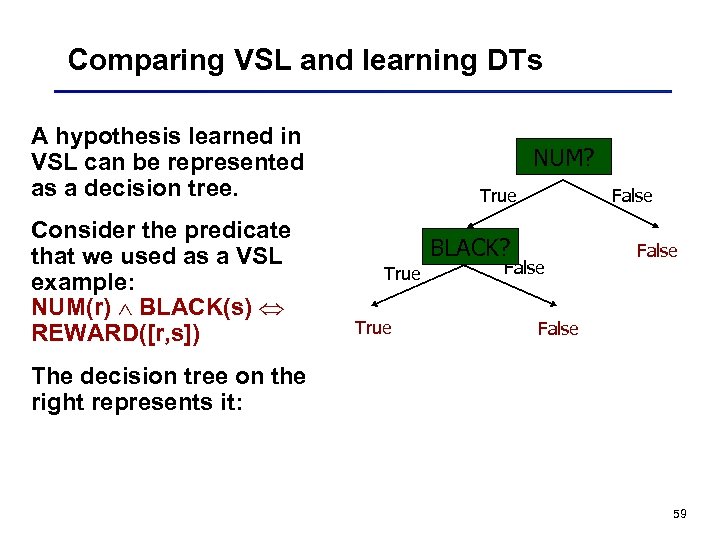
Comparing VSL and learning DTs A hypothesis learned in VSL can be represented as a decision tree. Consider the predicate that we used as a VSL example: NUM(r) BLACK(s) REWARD([r, s]) NUM? True False BLACK? True False The decision tree on the right represents it: 59
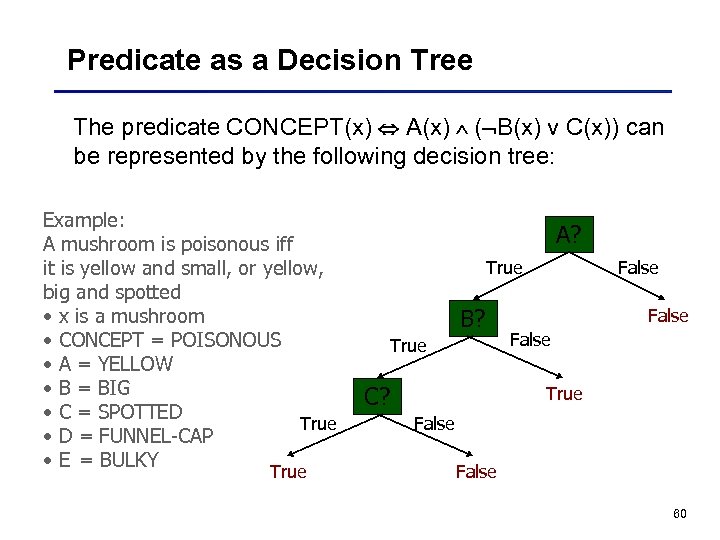
Predicate as a Decision Tree The predicate CONCEPT(x) A(x) ( B(x) v C(x)) can be represented by the following decision tree: Example: A mushroom is poisonous iff it is yellow and small, or yellow, big and spotted • x is a mushroom • CONCEPT = POISONOUS • A = YELLOW • B = BIG • C = SPOTTED True • D = FUNNEL-CAP • E = BULKY True A? True B? True C? False True False 60

Training Set Ex. # A B C D E CONCEPT 1 False True False 2 False True False 3 False True False 4 False True False 5 False True False 6 True False True 7 True False True 8 True False True 9 True False True 10 True True 11 True False 12 True False 13 True False True 61
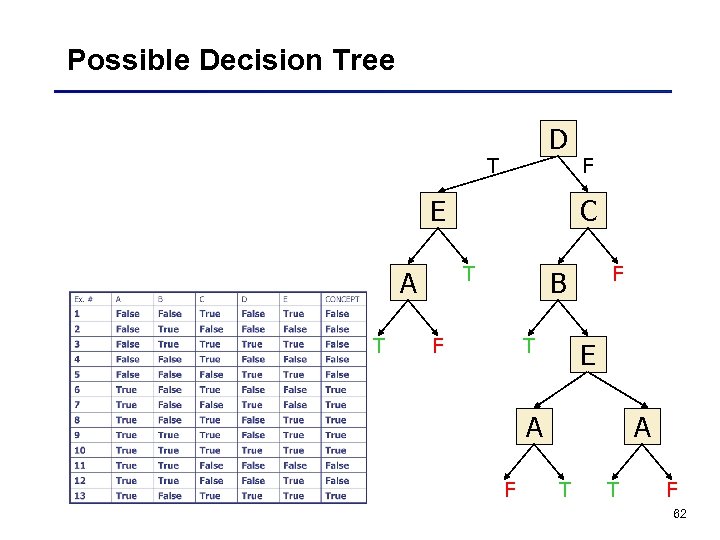
Possible Decision Tree D T E T C T A F F B F T E A A F T T F 62
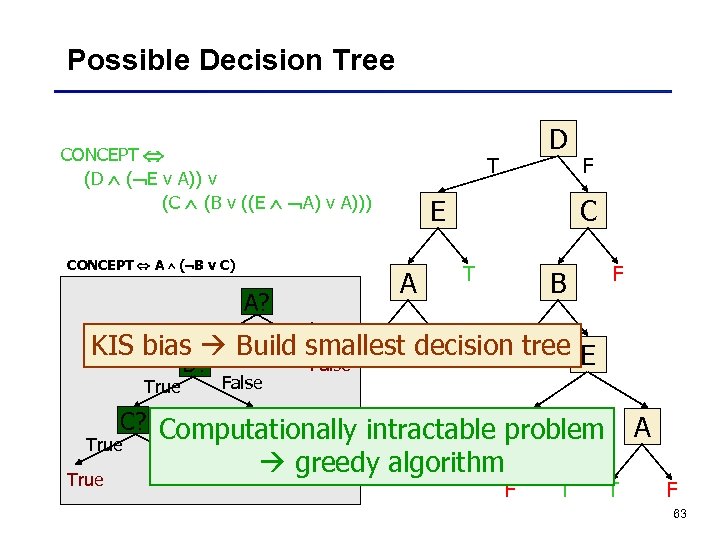
Possible Decision Tree CONCEPT (D ( E v A)) v (C (B v ((E A) v A))) CONCEPT A ( B v C) True T E A A? D F C T B F False T F T KIS bias Build smallest decision tree E False B? True False True C? Computationally intractable problem A False True False greedy algorithm F T A T F 63

Getting Started The distribution of the training set is: True: 6, 7, 8, 9, 10, 13 False: 1, 2, 3, 4, 5, 11, 12 64

Getting Started The distribution of training set is: True: 6, 7, 8, 9, 10, 13 False: 1, 2, 3, 4, 5, 11, 12 Without testing any observable predicate, we could report that CONCEPT is False (majority rule) with an estimated probability of error P(E) = 6/13 65

Getting Started The distribution of training set is: True: 6, 7, 8, 9, 10, 13 False: 1, 2, 3, 4, 5, 11, 12 Without testing any observable predicate, we could report that CONCEPT is False (majority rule) with an estimated probability of error P(E) = 6/13 Assuming that we will only include one observable predicate in the decision tree, which predicate should we test to minimize the probability of error? 66

Assume It’s A A T True: False: 6, 7, 8, 9, 10, 13 11, 12 F 1, 2, 3, 4, 5 If we test only A, we will report that CONCEPT is True if A is True (majority rule) and False otherwise The estimated probability of error is: Pr(E) = (8/13)x(2/8) + (5/8)x 0 = 2/13 67

Assume It’s B B T True: False: 9, 10 2, 3, 11, 12 F 6, 7, 8, 13 1, 4, 5 If we test only B, we will report that CONCEPT is False if B is True and True otherwise The estimated probability of error is: Pr(E) = (6/13)x(2/6) + (7/13)x(3/7) = 5/13 68

Assume It’s C C T True: False: 6, 8, 9, 10, 13 1, 3, 4 F 7 1, 5, 11, 12 If we test only C, we will report that CONCEPT is True if C is True and False otherwise The estimated probability of error is: Pr(E) = (8/13)x(3/8) + (5/13)x(1/5) = 4/13 69

Assume It’s D D T True: False: 7, 10, 13 3, 5 F 6, 8, 9 1, 2, 4, 11, 12 If we test only D, we will report that CONCEPT is True if D is True and False otherwise The estimated probability of error is: Pr(E) = (5/13)x(2/5) + (8/13)x(3/8) = 5/13 70

Assume It’s E E T True: False: 8, 9, 10, 13 1, 3, 5, 12 F 6, 7 2, 4, 11 So, only we will report that CONCEPT is is A If we test the. Ebest predicate to test False, independent of the outcome The estimated probability of error is unchanged: Pr(E) = (8/13)x(4/8) + (5/13)x(2/5) = 6/13 71

Choice of Second Predicate A F T C T True: False: 6, 8, 9, 10, 13 False F 7 11, 12 The majority rule gives the probability of error Pr(E|A) = 1/8 and Pr(E) = 1/13 72
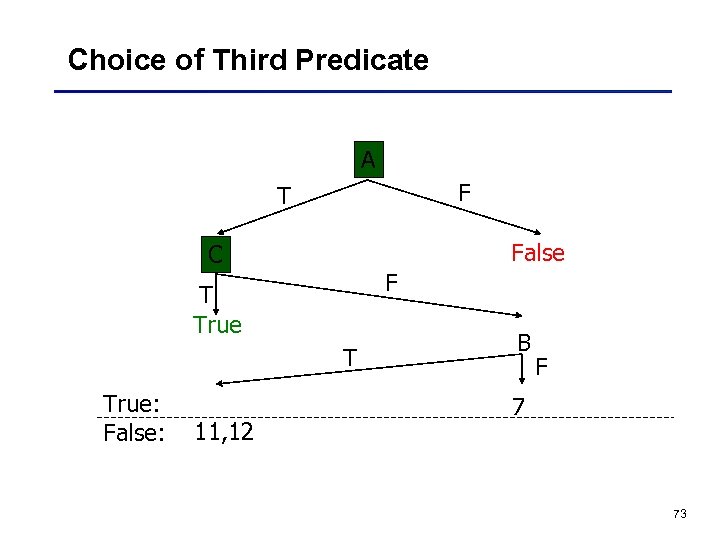
Choice of Third Predicate A F T False C F T True: False: 11, 12 B F 7 73
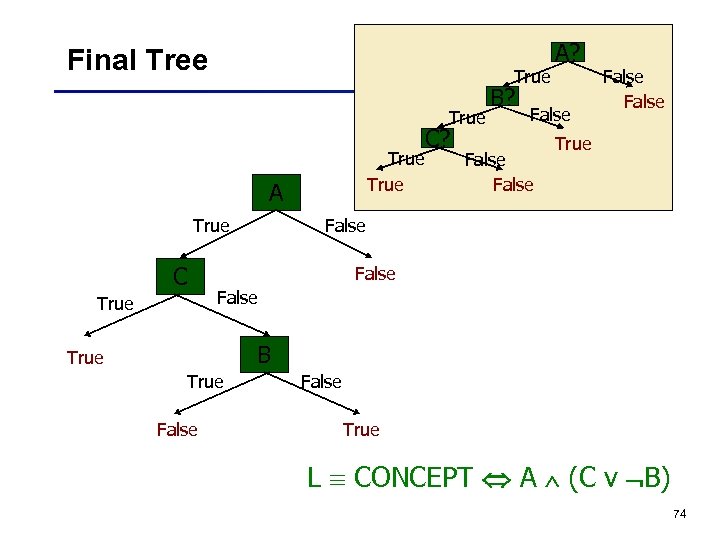
Final Tree True A True C C? B? A? False False True False True B True False True L CONCEPT A (C v B) 74

Learning a decision tree Function induce_tree (example_set, properties) begin if all entries in example_set are in the same class then return a leaf node labeled with that class else if properties is empty then return leaf node labeled with disjunction of all classes in example_set else begin select a property, P, and make it the root of the current tree; delete P from properties; for each value, V, of P begin create a branch of the tree labeled with V; let partitionv be elements of example_set with values V for property P; call induce_tree (partitionv, properties), attach result to branch V end If property V is Boolean: the partition will contain two 75 end sets, one with property V true and one with false end

What happens if there is noise in the training set? The part of the algorithm shown below handles this: if properties is empty then return leaf node labeled with disjunction of all classes in example_set Consider a very small (but inconsistent) training set: A T F F classification T F T A? True False True 76

Using Information Theory Rather than minimizing the probability of error, most existing learning procedures try to minimize the expected number of questions needed to decide if an object x satisfies CONCEPT. This minimization is based on a measure of the “quantity of information” that is contained in the truth value of an observable predicate and is explained in Section 9. 3. 2. We will skip the technique given there and use the “probability of error” approach. 77
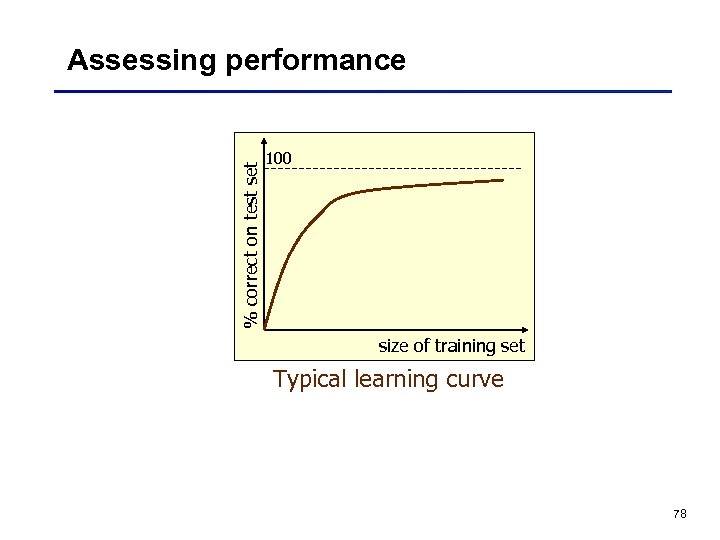
% correct on test set Assessing performance 100 size of training set Typical learning curve 78
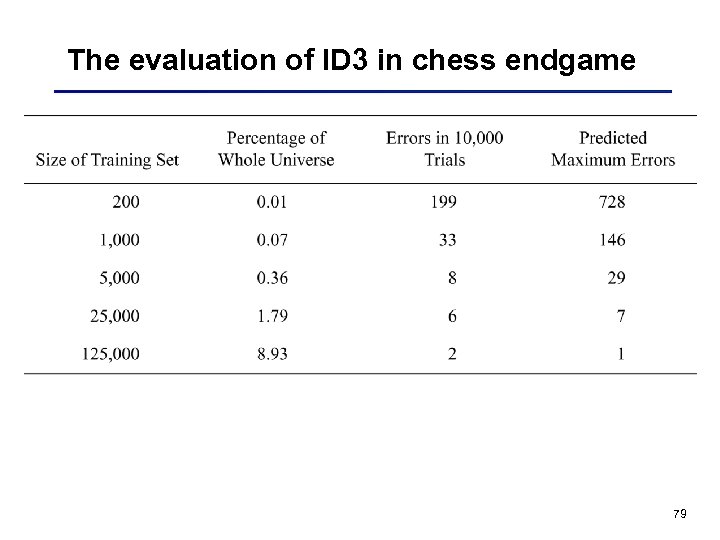
The evaluation of ID 3 in chess endgame 79

Other issues in learning decision trees • If data for some attribute is missing and is hard to obtain, it might be possible to extrapolate or use “unknown. ” • If some attributes have continuous values, groupings might be used. • If the data set is too large, one might use bagging to select a sample from the training set. Or, one can use boosting to assign a weight showing importance to each instance. Or, one can divide the sample set into subsets and train on one, and test on others. 80

Explanation based learning • Idea: can learn better when the background theory is known • Use the domain theory to explain the instances taught • Generalize the explanation to come up with a “learned rule” 81

Example • We would like the system to learn what a cup is, i. e. , we would like it to learn a rule of the form: premise(X) cup(X) • Assume that we have a domain theory: liftable(X) holds_liquid(X) cup(X) part (Z, W) concave(W) points_up holds_liquid (Z) light(Y) part(Y, handle) liftable (Y) small(A) light(A) made_of(A, feathers) light(A) • The training example is the following: cup (obj 1) small(obj 1) owns(bob, obj 1) part(obj 1, bowl) concave(bowl) small(obj 1) part(obj 1, handle) part(obj 1, bottom) points_up(bowl) color(obj 1, red) 82

First, form a specific proof that obj 1 is a cup (obj 1) liftable (obj 1) light (obj 1) part (obj 1, handle) holds_liquid (obj 1) part (obj 1, bowl) points_up(bowl) concave(bowl) small (obj 1) 83

Second, analyze the explanation structure to generalize it 84
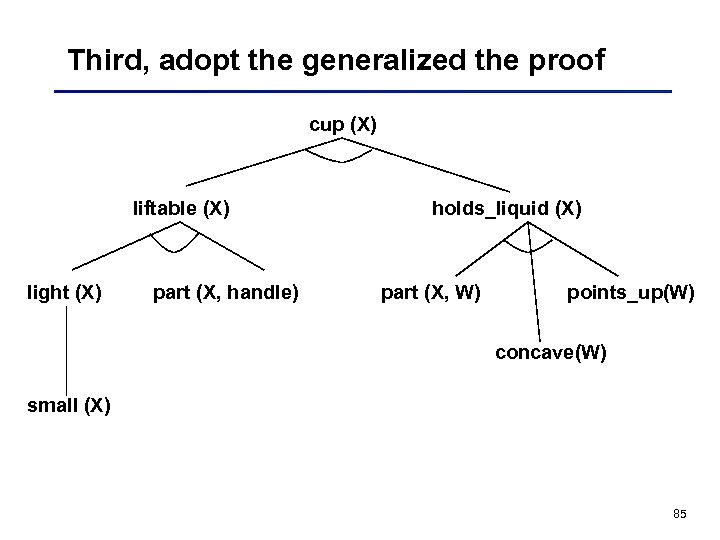
Third, adopt the generalized the proof cup (X) liftable (X) light (X) part (X, handle) holds_liquid (X) part (X, W) points_up(W) concave(W) small (X) 85

The EBL algorithm Initialize hypothesis = { } For each positive training example not covered by hypothesis: 1. Explain how training example satisfies target concept, in terms of domain theory 2. Analyze the explanation to determine the most general conditions under which this explanation (proof) holds 3. Refine the hypothesis by adding a new rule, whose premises are the above conditions, and whose consequent asserts the target concept 86

Wait a minute! • Isn’t this “just a restatement of what the learner already knows? ” • Not really · a theory-guided generalization from examples · an example-guided operationalization of theories • Even if you know all the rules of chess you get better if you play more • Even if you know the basic axioms of probability, you get better as you solve more probability problems 87

Comments on EBL • Note that the “irrelevant” properties of obj 1 were disregarded (e. g. , color is red, it has a bottom) • Also note that “irrelevant” generalizations were sorted out due to its goal-directed nature • Allows justified generalization from a single example • Generality of result depends on domain theory • Still requires multiple examples • Assumes that the domain theory is correct (errorfree)---as opposed to approximate domain theories which we will not cover. · This assumption holds in chess and other search problems. · It allows us to assume explanation = proof. 88

Two formulations for learning Inductive Analytical Given: • Instances • Hypotheses • Target concept • Training examples of the target concept • Domain theory for explaining examples Determine: • Hypotheses consistent with the training examples and the domain theory 89

Two formulations for learning (cont’d) Inductive Analytical Hypothesis fits data Hypothesis fits domain theory Statistical inference Deductive inference Requires little prior knowledge Learns from scarce data Syntactic inductive bias Bias is domain theory DT and VS learners are “similarity-based” Prior knowledge is important. It might be one of the reasons for humans’ ability to generalize from as few as a single training instance. Prior knowledge can guide in a space of an unlimited number of generalizations that can be produced by training examples. 90

An example: META-DENDRAL • Learns rules for DENDRAL • Remember that DENDRAL infers structure of organic molecules from their chemical formula and mass spectrographic data. • Meta-DENDRAL constructs an explanation of the site of a cleavage using · structure of a known compound · mass and relative abundance of the fragments produced by spectrography · a “half-order” theory (e. g. , double and triple bonds do not break; only fragments larger than two carbon atoms show up in the data) • These explanations are used as examples for constructing general rules 91

Analogical reasoning • Idea: if two situations are similar in some respects, then they will probably be in others • Define the source of an analogy to be a problem solution. It is a theory that is relatively well understood. • The target of an analogy is a theory that is not completely understood. • Analogy constructs a mapping between corresponding elements of the target and the source. 92
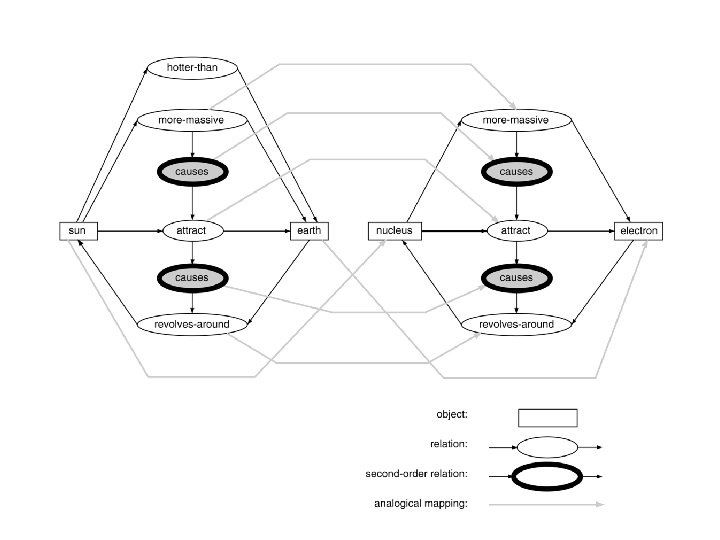

Example: atom/solar system analogy • The source domain contains: yellow(sun) blue(earth) hotter-than(sun, earth) causes(more-massive(sun, earth), attract(sun, earth)) causes(attract(sun, earth), revolves-around(earth, sun)) • The target domain that the analogy is intended to explain includes: more-massive(nucleus, electron) revolves-around(electron, nucleus) • The mapping is: sun nucleus and earth electron • The extension of the mapping leads to the inference: causes(more-massive(nucleus, electron), attract(nucleus, electron)) causes(attract(nucleus, electron), revolves 94 around(electron, nucleus))

A typical framework • Retrieval: Given a target problem, select a potential source analog. • Elaboration: Derive additional features and relations of the source. • Mapping and inference: Mapping of source attributes into the target domain. • Justification: Show that the mapping is valid. 95
c0d469eb6c7ec2e3be4e2d99751d7ccd.ppt