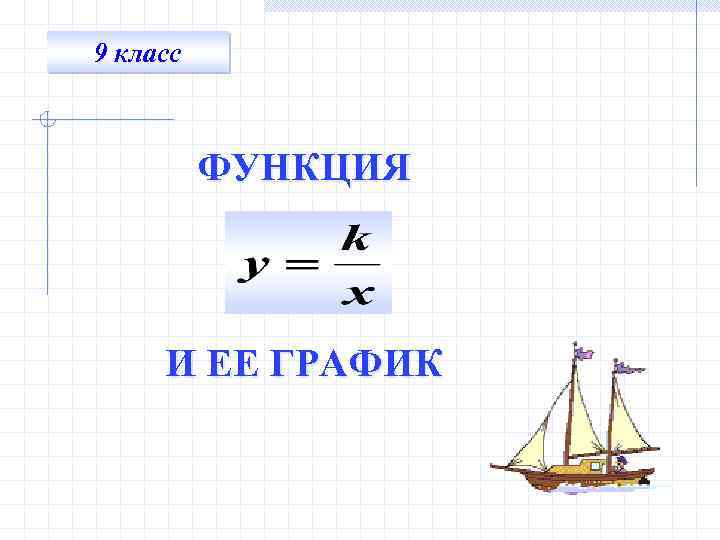9 класс ФУНКЦИЯ И ЕЕ ГРАФИК Функция

9 класс ФУНКЦИЯ И ЕЕ ГРАФИК

Функция Построение графика Свойства функции Физический смысл Сжатие и растяжение графика Сдвиг вдоль оси абсцисс Сдвиг вдоль оси ординат Примеры Задания

Ответы на кроссворд По горизонтали: По вертикали: 1. убывание 1. прямая 2. абсцисса 2. функция 3. график 3. парабола 4. возрастание 4. нечетность 5. ордината 5. четность

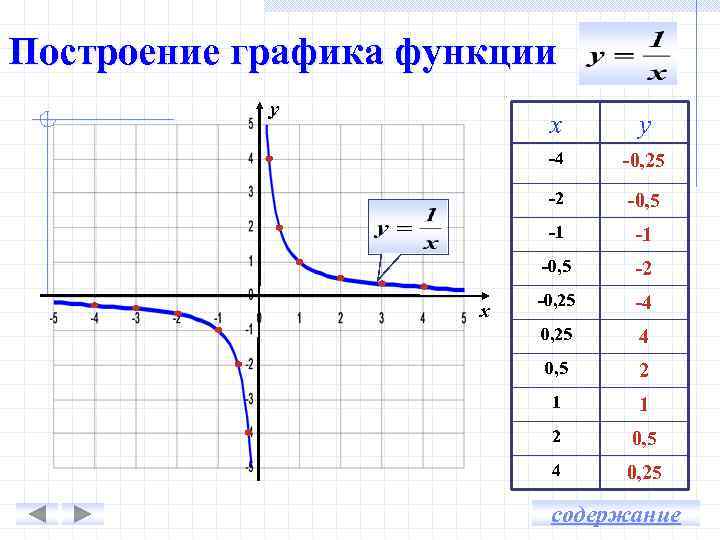Построение графика функции у х -4 -0, 25 -2 -0, 5 -1 -1 -0, 5 х у -2 -0, 25 -4 0, 25 4 0, 5 2 1 1 2 0, 5 4 0, 25 содержание

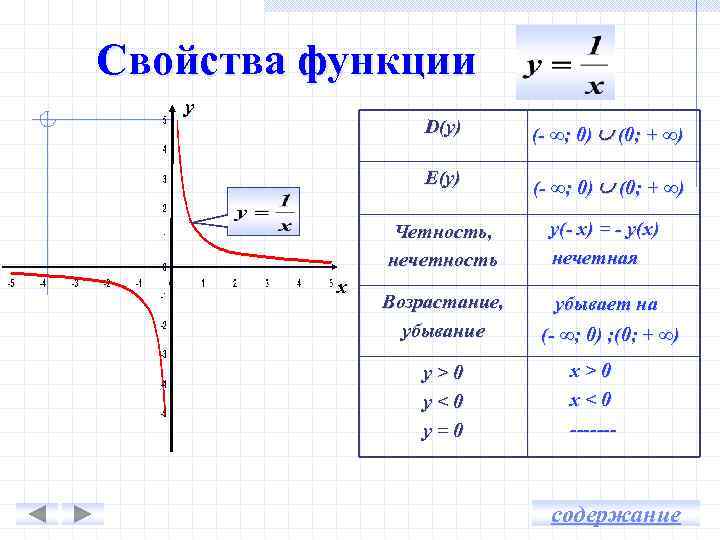Свойства функции у D(y) E(y) (- ∞; 0) (0; + ∞) Четность, нечетность х (- ∞; 0) (0; + ∞) у(- х) = - у(х) нечетная Возрастание, убывание убывает на y>0 y<0 y=0 (- ∞; 0) ; (0; + ∞) x>0 x<0 ------- содержание

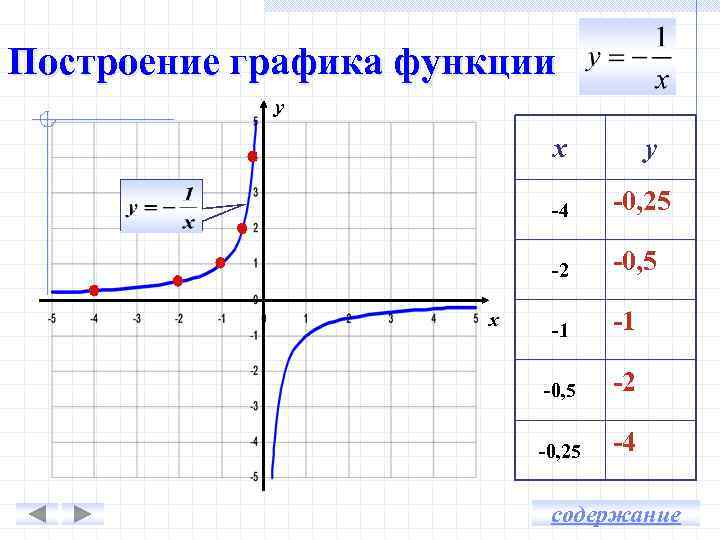Построение графика функции у х у -4 -2 х -0, 25 -0, 5 -1 -1 -0, 5 -2 -0, 25 -4 содержание

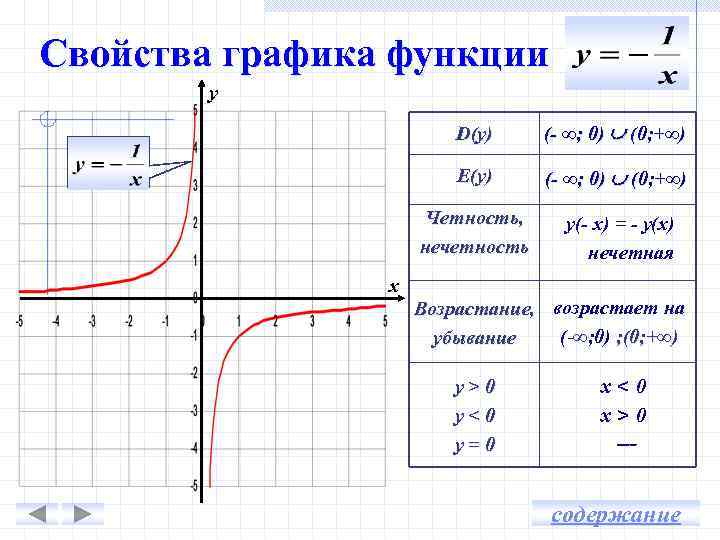Свойства графика функции у D(y) E(y) (- ∞; 0) (0; +∞) Четность, нечетность х (- ∞; 0) (0; +∞) у(- х) = - у(х) нечетная Возрастание, возрастает на (-∞; 0) ; (0; +∞) убывание y>0 y<0 y=0 х<0 х>0 --- содержание

Функция Обратная пропорциональность х – независимая переменная, k – отличное от нуля число, k > 0. График - гипербола. содержание

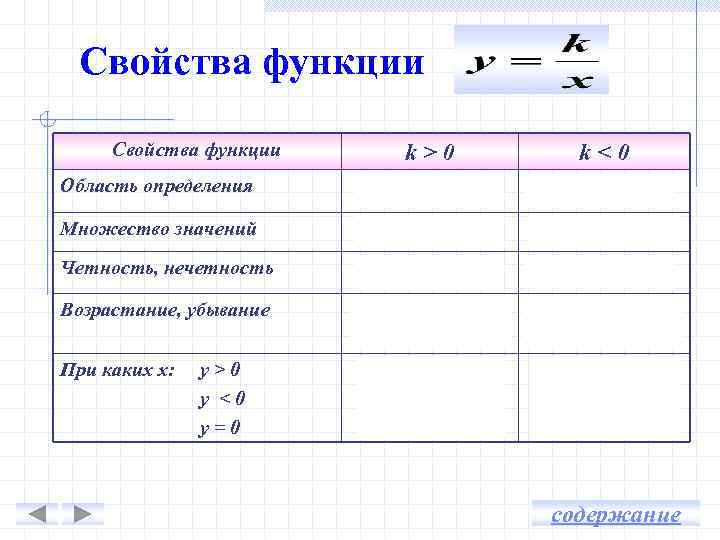Свойства функции k>0 k<0 Область определения (- ∞; 0); (0; + ∞) Множество значений (-∞; 0); (0; + ∞) (- ∞; 0); (0; + ∞) нечетная Четность, нечетность Возрастание, убывание При каких х: у>0 у <0 у=0 убывает возрастает на х > 0 и на х < 0 х>0 х<0 --- х<0 х>0 --- содержание

Физический смысл содержание

Задания 1. Заполните таблицу х 1 2 2, 5 6 16 60 160 2400 24 12 9, 6 4 1, 5 0, 4 0, 15 0, 01 2. Найдите число к и заполните таблицу х 1, 5 2, 5 4 6 5 6 12 24 40 24 15 10 12 10 5 2, 5 содержание

Сжатие и растяжение у х растяжение сжатие от ОХ вдоль ОУ в 2 раза к оси ОХ вдоль оси ОУ в 2 раза содержание

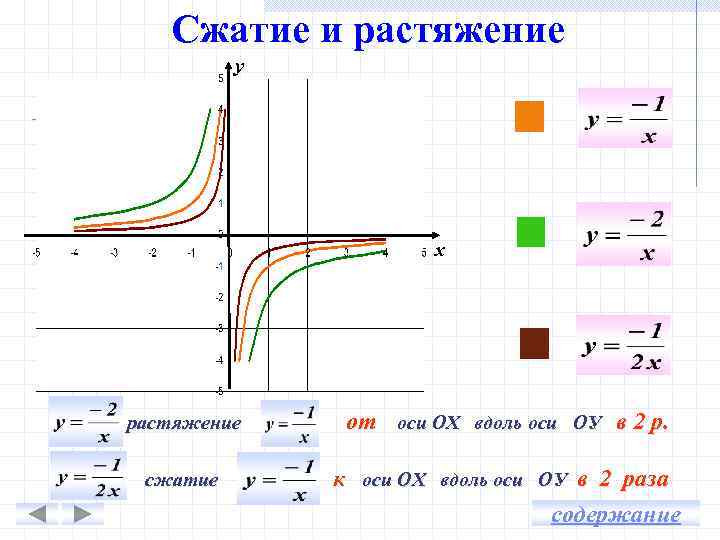Сжатие и растяжение у х растяжение от оси ОХ вдоль оси ОУ в 2 р. сжатие к оси ОХ вдоль оси ОУ в 2 раза содержание

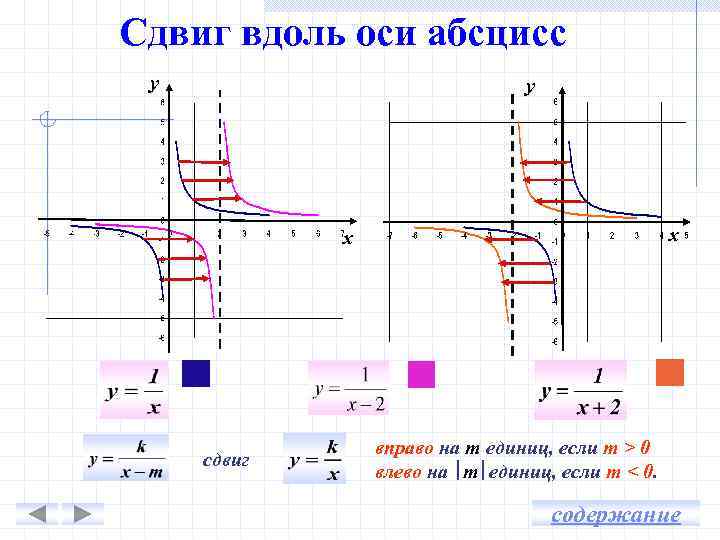Сдвиг вдоль оси абсцисс у у х х сдвиг вправо на m единиц, если m > 0 влево на ∣m∣единиц, если m < 0. содержание

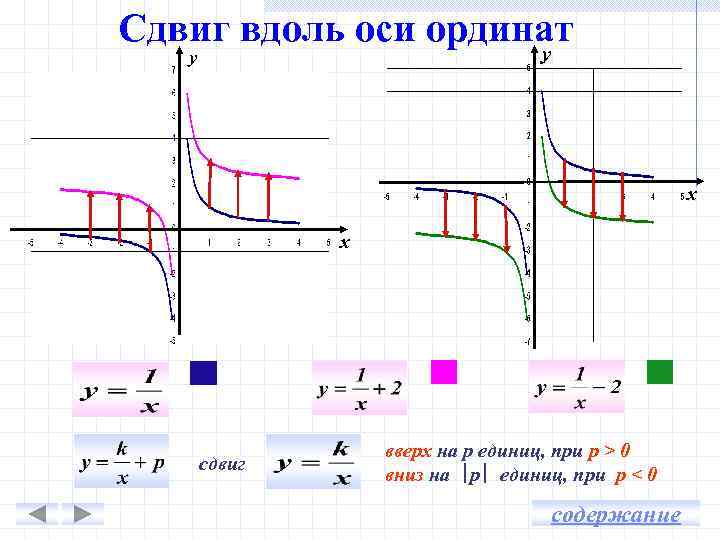Сдвиг вдоль оси ординат у у х х сдвиг вверх на р единиц, при р > 0 вниз на ∣р∣ единиц, при р < 0 содержание

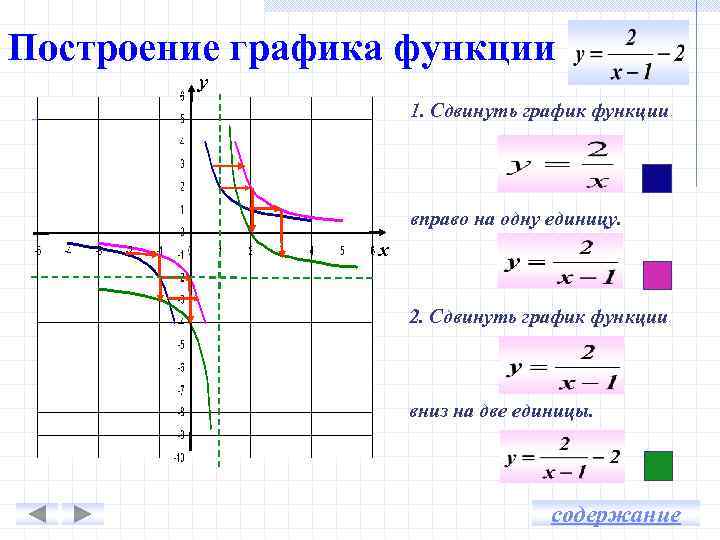Построение графика функции у 1. Сдвинуть график функции вправо на одну единицу. х 2. Сдвинуть график функции вниз на две единицы. содержание

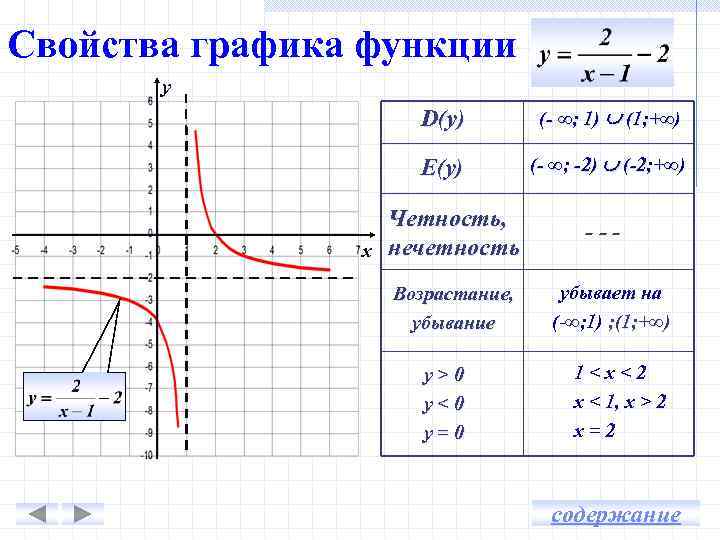Свойства графика функции у D(y) (- ∞; 1) (1; +∞) E(y) (- ∞; -2) (-2; +∞) Четность, х нечетность --- Возрастание, убывание y>0 y<0 y=0 убывает на (-∞; 1) ; (1; +∞) 1<х<2 х < 1, х > 2 х=2 содержание

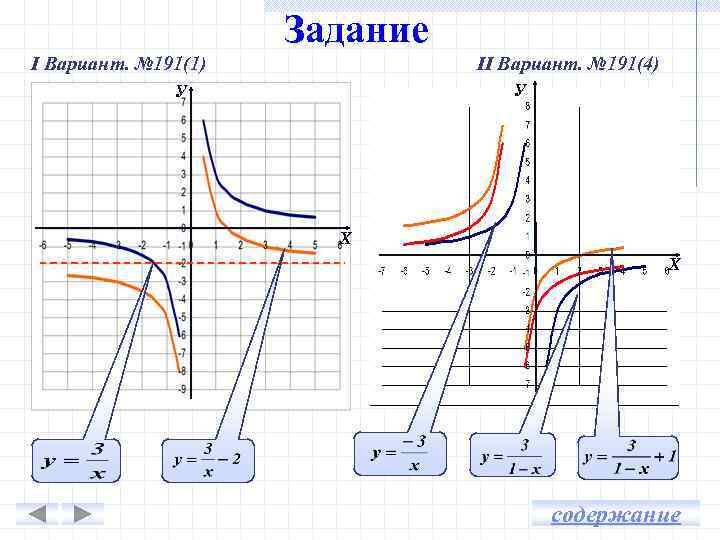Задание I Вариант. № 191(1) II Вариант. № 191(4) У У Х Х содержание

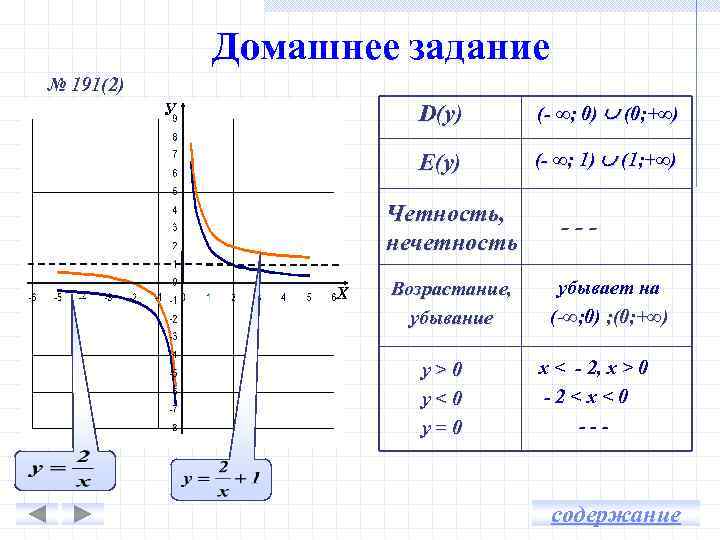Домашнее задание № 191(2) D(y) (- ∞; 0) (0; +∞) E(y) У (- ∞; 1) (1; +∞) Четность, нечетность Х Возрастание, убывание y>0 y<0 y=0 --убывает на (-∞; 0) ; (0; +∞) х < - 2, х > 0 -2<х<0 --- содержание

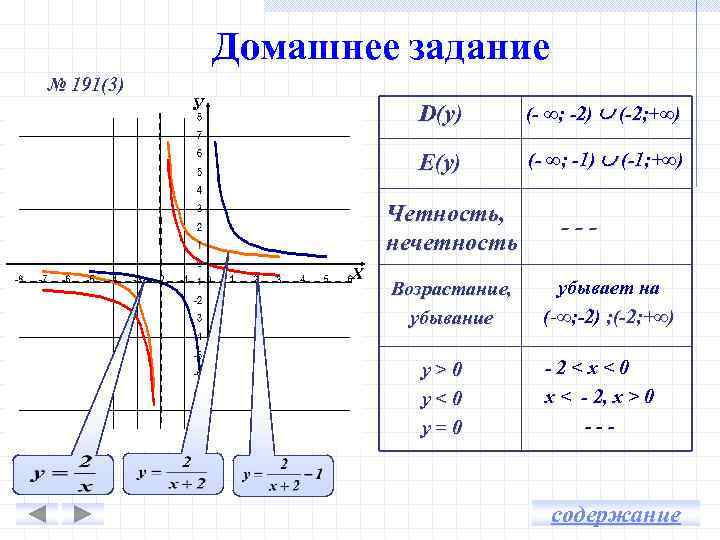Домашнее задание № 191(3) У D(y) (- ∞; -2) (-2; +∞) E(y) (- ∞; -1) (-1; +∞) Четность, нечетность Х Возрастание, убывание y>0 y<0 y=0 --убывает на (-∞; -2) ; (-2; +∞) -2<х<0 х < - 2, х > 0 --- содержание

Литература Колягин Ю. М. , Сидоров Ю. В. и др. Изучение алгебры в 7 -9 классах: Книга для учителя. – М. : Просвещение, 2002. Алимов Ш. А. , Колягин Ю. М. и др. Алгебра: Учебник для 9 класса общеобразовательных учреждений. – М. : Просвещение, 2003.