9 класс Федорова Татьяна Федоровна 2009

9 класс © Федорова Татьяна Федоровна, 2009

Содержание 1. Длина окружности 2. Число π 3. Длина дуги окружности 4. Площадь круга 5. Площадь кругового сектора 6. Итог урока

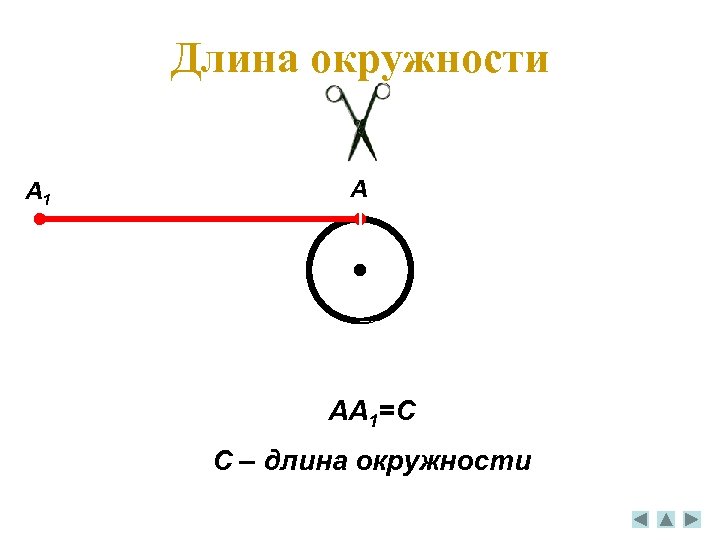Длина окружности A 1 A AA 1=C C – длина окружности

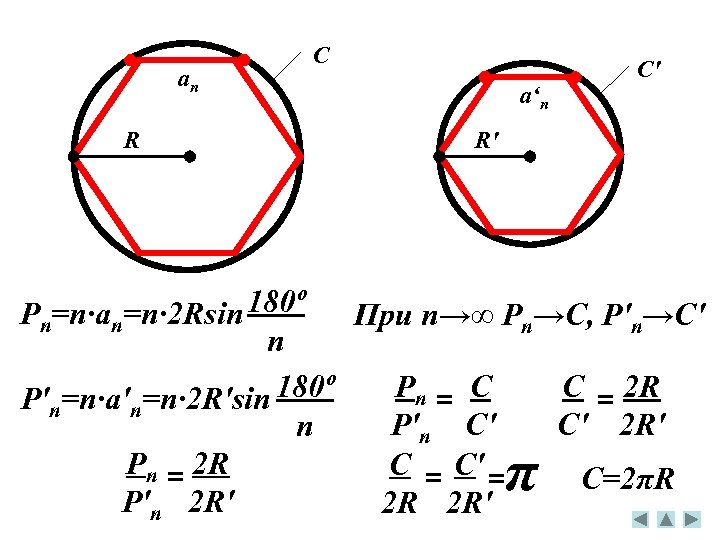an R C a‘n C' R' Pn=n·an=n· 2 Rsin 180º При n→∞ Pn→C, P'n→C' n Pn = C C = 2 R P'n=n·a'n=n· 2 R'sin 180º P'n C' C' 2 R' n Pn = 2 R C = C' = C=2πR P'n 2 R' 2 R 2 R' π

π – бесконечная непериодическая десятичная дробь. π=3, 1415926535897932384626433832795… 22 π≈ 7 Приближенное значение с точностью до 0, 002 было найдено в III в. до н. э. греческим ученым Архимедом. При решении задач обычно пользуются приближенным значением π с точностью до 0, 01: π≈3, 14.

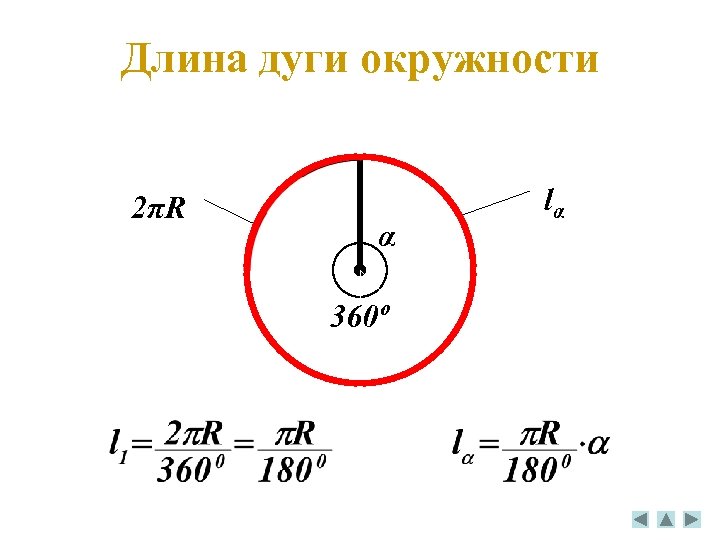Длина дуги окружности 2πR α 360º lα

Площадь круга A 2 A 3 rn A 1 R An S=πR 2

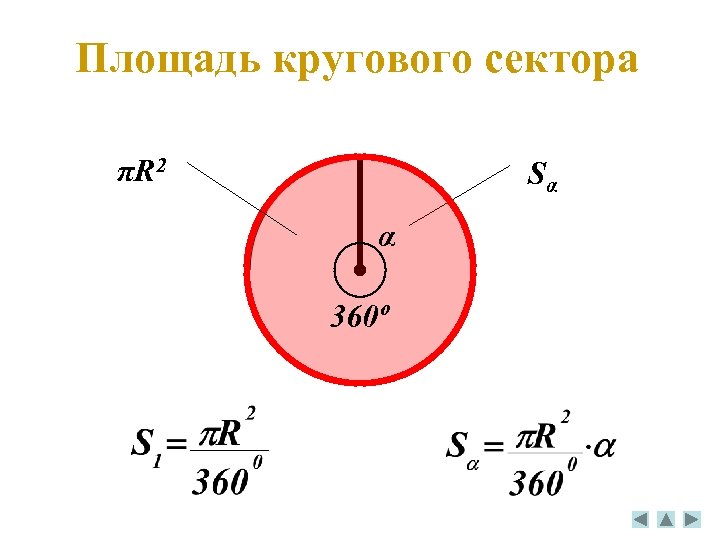Площадь кругового сектора πR 2 Sα α 360º

Проверь свои знания • Как изменится длина окружности, если радиус окружности увеличить в три раза? • Как изменится радиус окружности, если длину окружности уменьшить в k раз? • Как изменится площадь круга, если его радиус увеличить в k раз?