9 Анализ и прогнозирование временных рядов 9 1

9. Анализ и прогнозирование временных рядов 9. 1. Понятие и классификация рядов динамики 9. 2. Показатели изменения уровней ряда динамики 9. 3. Компонентный состав временного ряда 9. 4. Методы выявления тренда 9. 5. Методы сглаживания 9. 6. Аналитическое выравнивание. Прогнозирование тенденций развития с помощью моделей кривых роста 9. 7. Методы выбора кривых роста 9. 8. Доверительные интервалы прогноза. Оценка адекватности и точности моделей

Под прогнозом понимается научно обоснованное описание возможных состояний объектов в будущем, а также альтернативных путей и сроков достижения этого состояния. Процесс разработки прогнозов называется прогнозированием (от греч. prognosis – предвидение, предсказание) и предполагает выявление ответов на два вопроса: 1. Что вернее всего ожидать в будущем? 2. Каким образом нужно изменить условия, чтобы достичь заданного конечного состояния прогнозируемого объекта? Прогнозы, отвечающие на вопросы первого типа, называются поисковыми, второго – нормативными.

По времени упреждения экономические прогнозы можно разделить на следующие виды: n оперативные (до одного месяца); n краткосрочные (от одного, нескольких месяцев до года); n среднесрочные (более 1 года, но не превышает 5 лет); n долгосрочные (более 5 лет). В зависимости от масштабности объекта прогнозирования могут охватывать микро-, мезо -, макро-уровни, а также глобальный уровень.

Статистические методы прогнозирования опираются на анализ временных рядов. Временным рядом (рядом динамики, динамическим рядом – time series) называется последовательность значений статистического показателя (признака), упорядоченного в хронологическом порядке, т. е. в порядке возрастания временного параметра. Отдельные наблюдения временного ряда называются уровнями этого ряда. Каждый ряд динамики содержит два элемента: 1) значения времени; 2) соответствующие им значения уровней ряда.

Ряды динамики классифицируют следующим образом. 1. В зависимости от способа выражения уровней различают ¨ ряд абсолютных величин, ¨ ряд средних величин, ¨ ряд относительных величин. 2. В зависимости от того, как уровни ряда отражают состояние явления: на определенные моменты времени (начало месяца, квартала, года и т. п. ) или за определенные интервалы времени (за сутки, месяц, год и т. п. ), различают соответственно ¨ моментные и ¨ интервальные ряды динамики. 3. В зависимости от расстояния между уровнями ряды динамики могут быть с ¨ равноотстоящими уровнями и ¨ неравноотстоящими уровнями во времени. 4. В зависимости от наличия основной тенденции изучаемого процесса ряды динамики бывают ¨ стационарными и ¨ нестационарными. 5. По числу показателей можно выделить ¨ изолированные и ¨ комплексные (многомерные) ряды динамики.

При составлении ряда динамики должны выполняться следующие требования. 1. Периодизация развития, то есть расчленение его во времени на однородные этапы, в пределах которых показатель подчиняется одному закону развития. Это, по существу, типологическая группировка во времени. Периодизация может осуществляться несколькими методами: ¨ ¨ ¨ 2. 3. 4. исторический метод, метод параллельной периодизации, методы многомерного статистического анализа. Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета. Величины временных интервалов должны соответствовать интенсивности изучаемых процессов. Числовые уровни рядов динамики должны быть упорядоченными во времени. Не допускается анализ рядов с пропусками отдельных уровней, если же такие пропуски неизбежны, то их восполняют условными расчетными значениями.

К числу основных задач, возникающих при изучении динамических рядов, относятся: 1) характеристика интенсивности изменений в уровнях ряда динамики; 2) определение средних показателей динамических рядов; 3) выявление основных закономерностей (тенденции) развития изучаемого явления; 4) выявление факторов, обуславливающих изменение изучаемого явления; 5) прогноз развития явления.

9. 2. Показатели изменения уровней ряда динамики

При изучении явления во времени встает проблема описания интенсивности изменения и расчета средних показателей динамики. Решается она путем построения соответствующих показателей. Для характеристики интенсивности изменения во времени такими показателями являются: n абсолютный прирост, n темпы роста, n темпы прироста, n абсолютное значение одного процента прироста. В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели. Если же сравнение производится с предыдущим периодом или моментом времени, то говорят о цепных показателях.

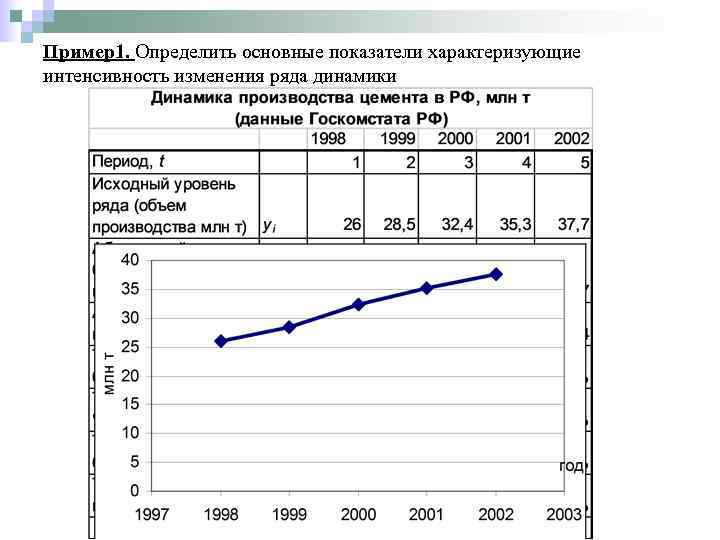Пример1. Определить основные показатели характеризующие интенсивность изменения ряда динамики

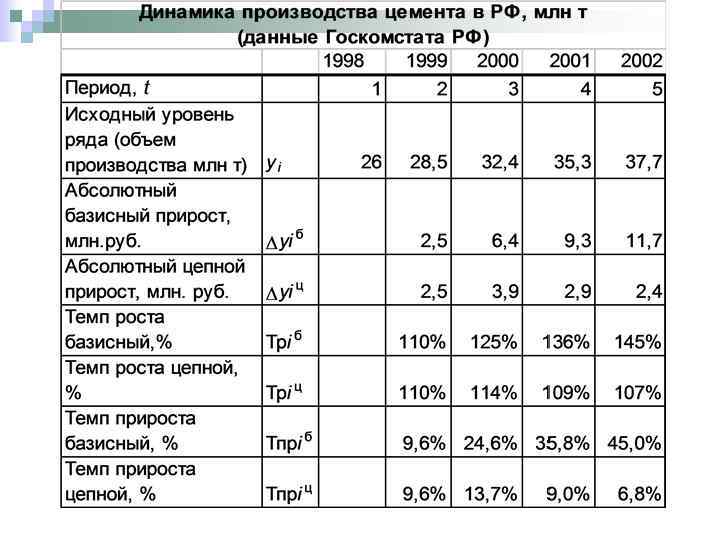
Система средних показателей включает: n средний уровень, n средний абсолютный прирост, n средний темп роста, n средний темп прироста.

В примере 1 мы имеем интервальный ряд динамики с равноотстоящими уровнями во времени, поэтому средний уровень ряда рассчитаем по формуле средней арифметической простой: итог суммирования уровней за весь период число периодов. Средний объем производства за пять лет составил:

Если интервальный ряд динамики имеет неравноотстоящие уровни, то средний уровень ряда вычисляется по формуле средней арифметической взвешенной: где ti - число периодов времени, в течение которых уровень не изменяется. Для моментного ряда с равноотстоящими уровнями средний уровень ряда вычисляется по формуле средней хронологической.

Пример 2.

Пример 3.

Средний абсолютный прирост определяется по формуле: В примере 1 среднегодовой прирост производства цемента за 1998 -2002 гг. равен:

Средней темп роста вычисляется по формуле средней геометрической из цепных темпов роста: Среднегодовой темп роста производства цемента за 19982002 г. (пример 1) равен:

Средний темп прироста равен: В примере 1:

Простейшие приемы прогнозирования Используемый аналитический показатель Формула для расчета прогноза Средний абсолютный прирост L – период опережения Средний коэффициент роста (средний темп роста не в процентном выражении ) Средний коэффициент прироста (средний темп прироста не в процентом выражении ) Условия применения Близость динамики показателя у линейному развитию. Незначительная вариация цепных абсолютных приростов Близость динамики к развитию по показательной (экспоненциальной) кривой. Незначительная вариация цепных темпов роста (прироста)

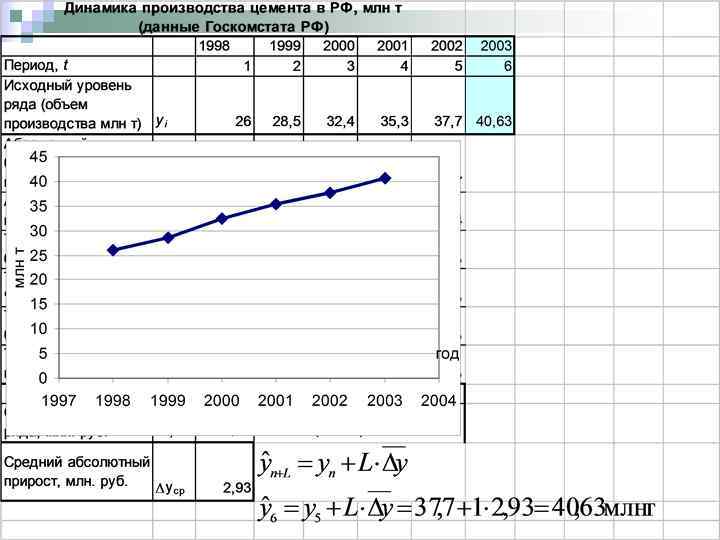
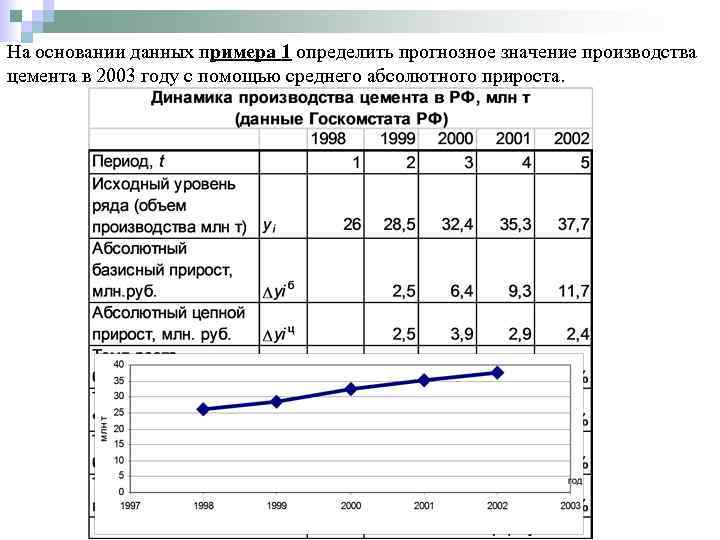На основании данных примера 1 определить прогнозное значение производства цемента в 2003 году с помощью среднего абсолютного прироста.

Пример 4. Количество вкладов физических лиц в отделениях банка изменялось с примерно постоянным темпом роста в течении пяти лет. На начало первого года количество вкладов составило 7875, на начало пятого года – 10104. Требуется рассчитать прогноз количества вкладов физических лиц в исследуемых отделениях банка на начало шестого года, используя средний темп роста.

9. 3. Компонентный состав временного ряда

Значения уровней временных рядов могут содержать следующие компоненты: n тренд (основная тенденция динамического ряда) – систематическая составляющая долговременного действия; n периодическая составляющая: ¨ сезонная компонента (период колебаний не превышает 1 года); ¨ циклическая компонента (период колебаний больше года – циклы деловой активности Кондратьева, демографические, инвестиционные и другие циклы); n нерегулярная компонента (случайная составляющая). Выделяют два вида факторов, под действием которых формируется нерегулярная компонента: ¨ факторы резкого, внезапного действия (стихийные бедствия, эпидемия, война, кризис и др. ); ¨ текущие факторы вызывают случайные колебания (влияние каждого из текущих факторов незначительно, но ощущается их суммарное воздействие).

Если временной ряд представляется в виде суммы соответствующих компонент, то полученная модель носит название аддитивной (от англ. to add – добавлять): yt=ut+st+vt+ t. Представление временного ряда в виде произведения компонент соответствует мультипликативной модели: yt=ut·st·vt· t, где yt – уровни временного ряда, ut – трендовая составляющая, st – сезонная компонента, vt – циклическая компонента, t – случайная компонета. Выделяют модели смешанного типа, Например: yt=ut·st·vt+ t.

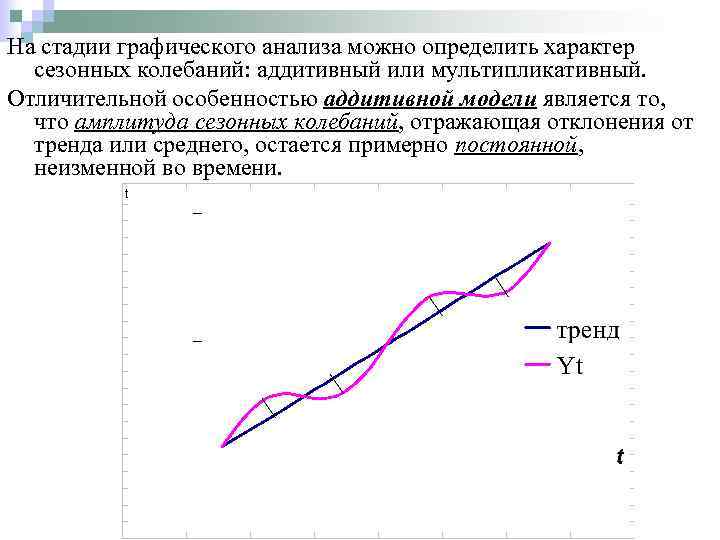На стадии графического анализа можно определить характер сезонных колебаний: аддитивный или мультипликативный. Отличительной особенностью аддитивной модели является то, что амплитуда сезонных колебаний, отражающая отклонения от тренда или среднего, остается примерно постоянной, неизменной во времени.

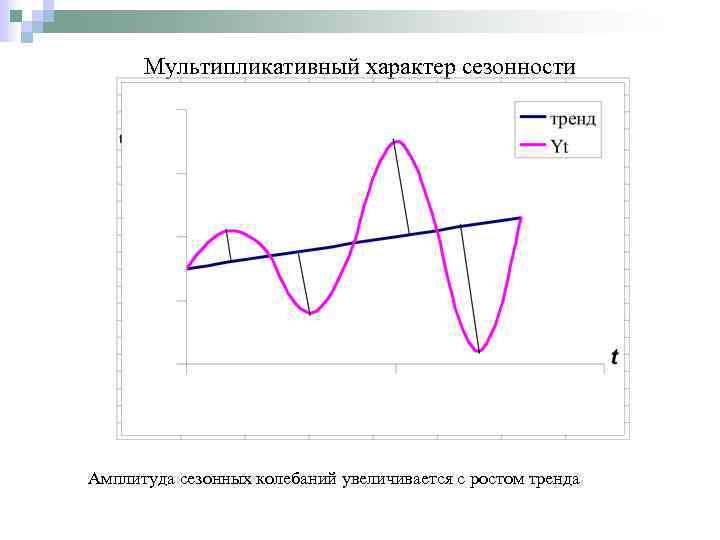Мультипликативный характер сезонности Амплитуда сезонных колебаний увеличивается с ростом тренда

Изучение тренда включает три основных этапа: 1. проверка ряда динамики на наличие тренда; 2. выравнивание временного ряда; 3. непосредственное выделение тренда с экстраполяцией полученных результатов.

9. 4. Методы выявления тренда

Методы выявления тренда целесообразно использовать на слабо выраженных зависимостях. Если на графике видно тренд, то методы выявления тренда использовать нецелесообразно. В настоящее время известно около десятка критериев для проверки наличия тренда, различающихся как по мощности, так и по сложности математического аппарата. Наиболее известными являются: 1. Метод средних. Изучаемый ряд динамики разбивается на несколько интервалов (обычно на два), для каждого из которых определяется средняя величина. Выдвигается гипотеза о существенном различии средних. Если эта гипотеза принимается, то признается наличие тренда. 2. Метод Фостера – Стюарта кроме определения наличия тенденции явления позволяет обнаружить тренд дисперсии уровней ряда динамики, что важно знать при анализе и прогнозировании экономических явлений. 3. Критерий серий, основанный на медиане.

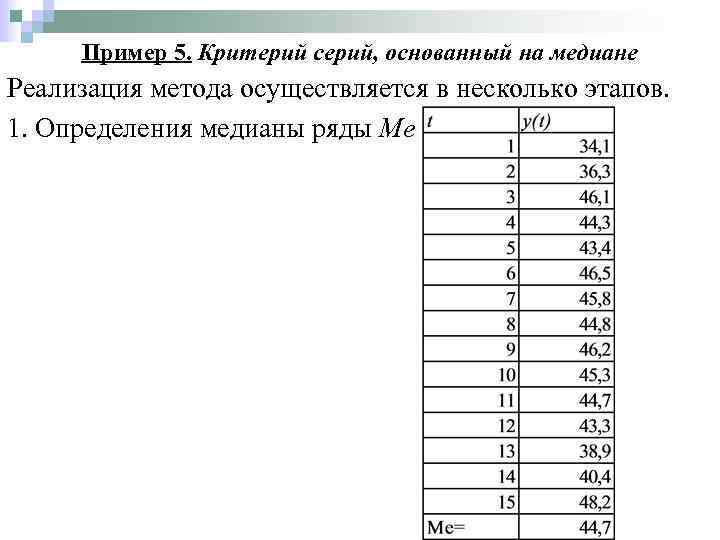Пример 5. Критерий серий, основанный на медиане Реализация метода осуществляется в несколько этапов. 1. Определения медианы ряды Me

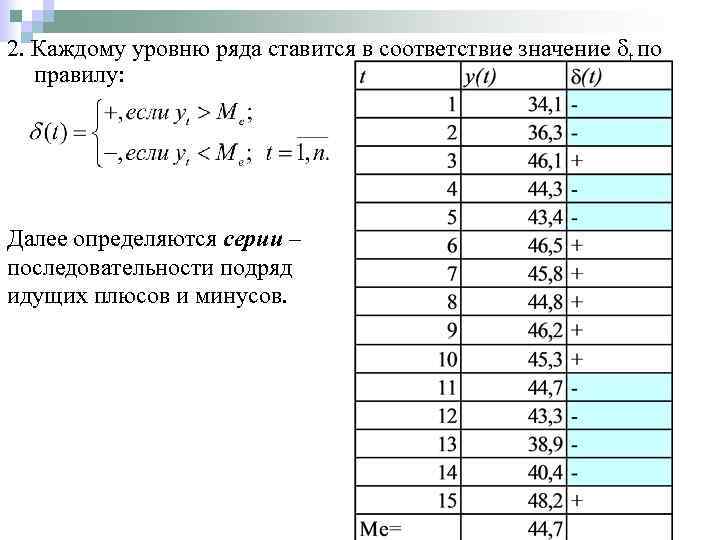2. Каждому уровню ряда ставится в соответствие значение t по правилу: Далее определяются серии – последовательности подряд идущих плюсов и минусов.

3. Подсчитываются наблюдаемые значения двух показателей: n (n) – число серий в совокупности (t); n max(n) – протяженность самой длинной серии. Соответствующие критические значения (для 5% уровня значимости) рассчитываются по формулам:

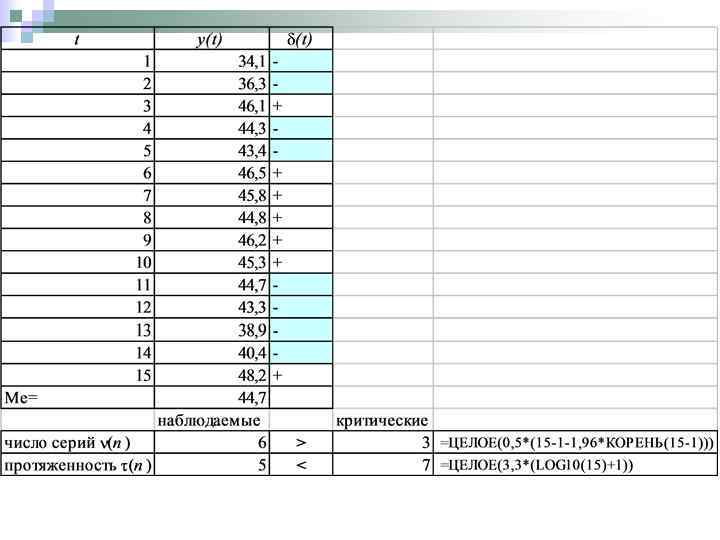
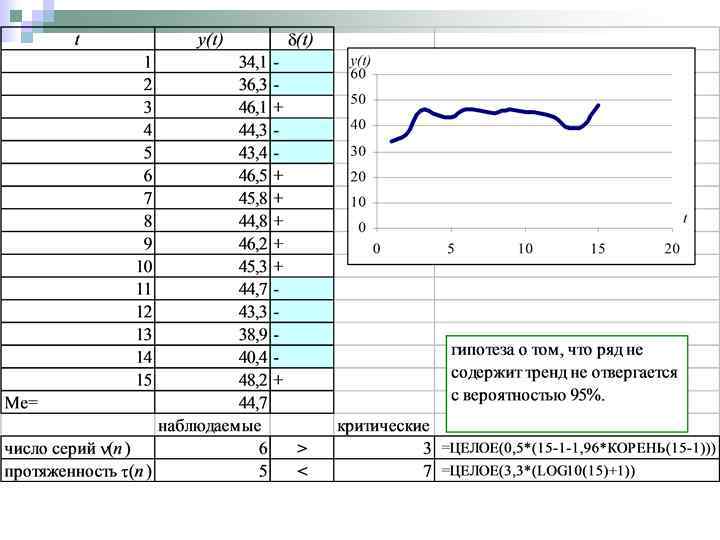
4. Проверка гипотезы об отсутствии тренда основывается на сравнении наблюдаемых и критических значений числа серий и максимальной протяженности серии. Смысл критерия состоит в том, что в отсутствии тренда максимальная протяженность серии не должна быть слишком большой, а число серий слишком маленьким. Поэтому критерий формулируется следующим образом: n если выполняется: то с вероятностью 95% гипотеза не отвергается; n Если хотя бы одно из неравенств системы не выполняется, то гипотеза отвергается с вероятностью ошибки 5%.

9. 5. Методы сглаживания 9. 5. 1. Использование метода скользящих средних 9. 5. 2. Экспоненциальное сглаживание.

Методы сглаживания разделяют на две основные группы: 1) сглаживание или механическое выравнивание отдельных членов ряда динамики с использованием фактических значений соседних уровней; 2) выравнивание с применением кривой, проведенной между конкретными уровнями таким образом, чтобы она отображала тенденцию, присущую ряду, и одновременно освободила его от незначительных колебаний. Рассмотрим методы, относящиеся к первой группе. Укрупнение интервалов. Ряд динамики разделяют на некоторое достаточно большое число равных интервалов. Если средние уровни по интервалам не позволяют увидеть тенденцию развития явления, переходят к расчету уровней за большие промежутки времени, увеличивая длину каждого интервала (одновременно уменьшается количество интервалов). Метод скользящей средней. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Экспоненциальное сглаживание. Применяется для предсказания значения на основе прогноза для предыдущего периода, скорректированного с учетом погрешностей в этом прогнозе.

9. 5. 1. Использование метода скользящих средних n. Сглаживание временных рядов с помощью простых скользящих средних n. Особенности применения взвешенных скользящих средних

Метод простой скользящей средней. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Целое число уровней, по которым рассчитывается среднее значение, называют интервалом сглаживания. Формулы расчета по скользящей средней в середине ряда выглядят, в частности, следующим образом: n для 3 – членной n для 5 – членной

Недостаток методики сглаживания скользящими средними состоит в условности определения сглаженных уровней для точек в начале и конце ряда. Получают их специальными приемами – расчетом средней арифметической взвешенной. Так, при сглаживании по трем точкам выровненное значение в начале ряда рассчитывается по формуле: Для последней точки расчет симметричен. При сглаживании по пяти точкам имеем: Для последних двух точек ряда расчет сглаженных значений

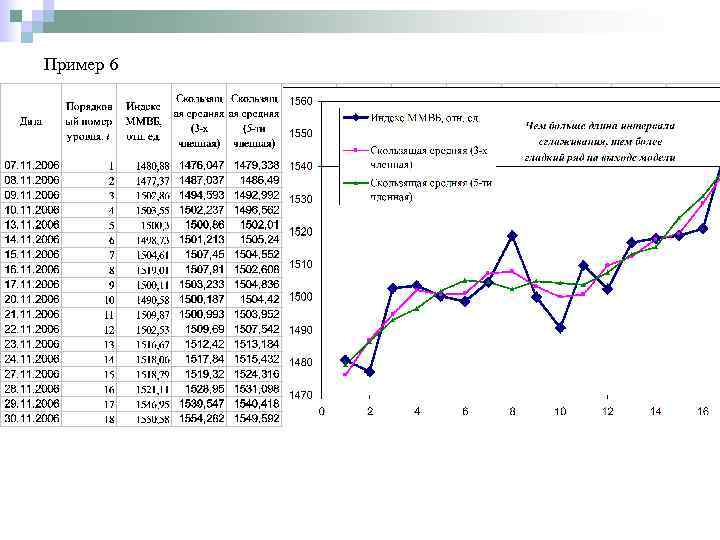Пример 6

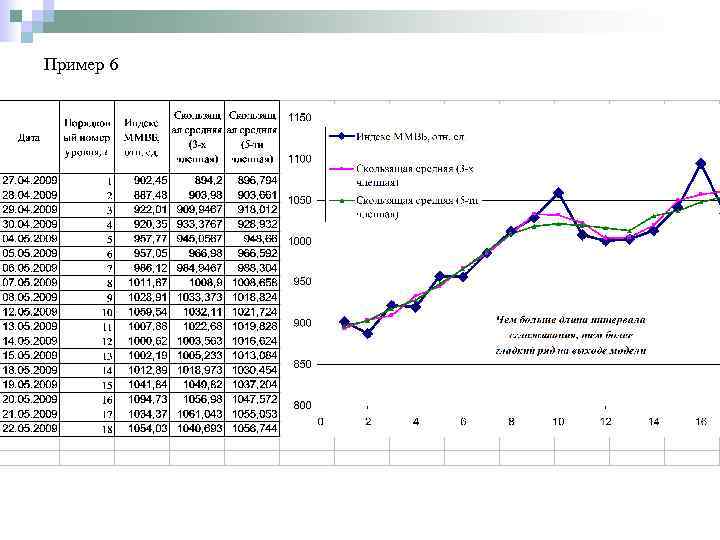Пример 6

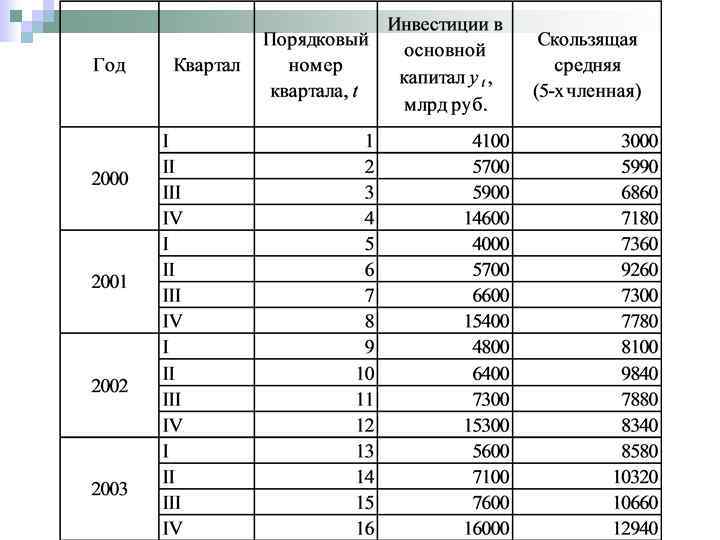
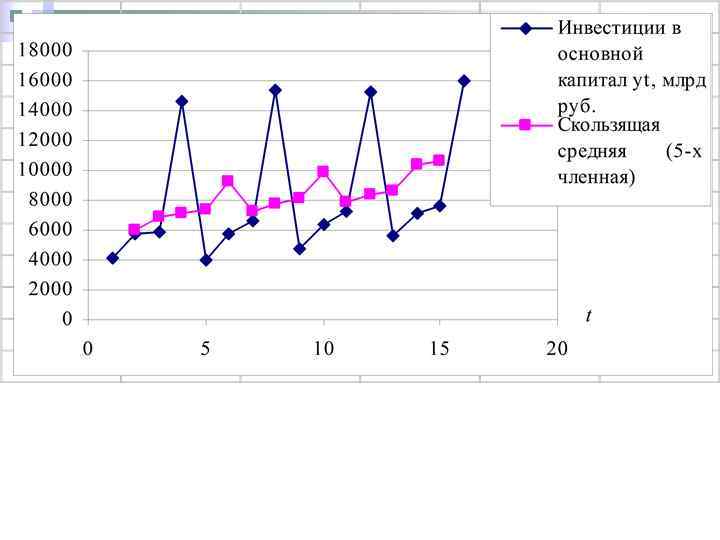
Пример 7. В табл. Приведены квартальные данные за четыре года об объеме инвестиций в основной капитал в РФ в фактически действующих ценах (stat. hse. ru). Ежегодно в четвертом квартале наблюдаются существенные всплески в значениях показателя. Наиболее низкие значения инвестиций в основной капитал характерны для уровней, соответствующих первому кварталу каждого года. Для сглаживания колебаний примените процедуру скользящих средних, приняв длину интервала сглаживания равную 3.

Особенности применения взвешенных скользящих средних Простую скользящую среднюю следует применять в тех случаях, когда графическое изображение динамического ряда напоминает прямую. Если для процесса характерно нелинейное развитие, то простая скользящая средняя может привести к существенным искажениям. Когда тренд выравниваемого ряда имеет сгибы и для исследователя желательно сохранить волны, то целесообразно использовать возвещенную скользящую среднюю.

Весовые коэффициенты для расчета скользящей средней Длина интервала сглаживания 5 7 9 11 13 Весовые коэффициенты

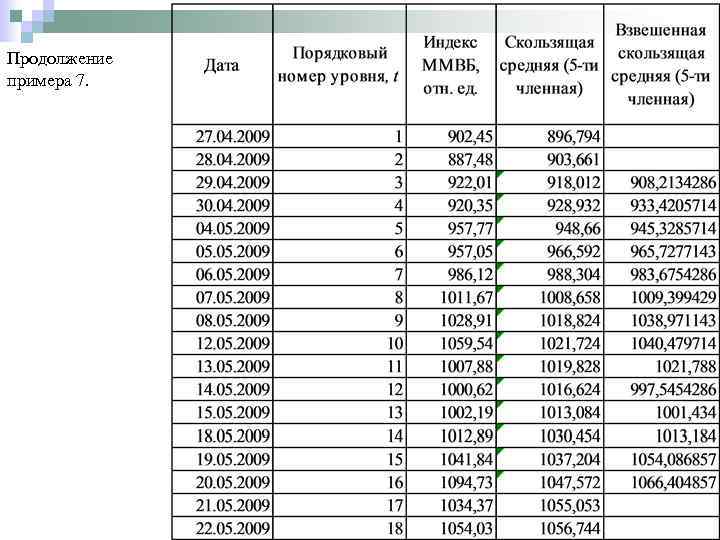Продолжение примера 7.

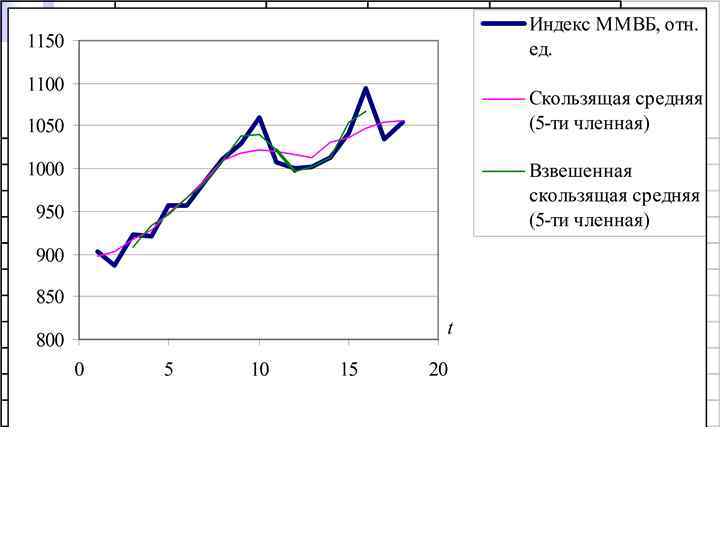
9. 5. 2. Экспоненциальное сглаживание.

Экспоненциальное сглаживание применяется для предсказания значения на основе прогноза для предыдущего периода, скорректированного с учетом погрешностей в этом прогнозе. При анализе используется константа сглаживания , по величине которой определяется степень влияния на прогнозы погрешностей в предыдущем прогнозе. Базовое уравнение экспоненциального сглаживания имеет вид: где – фактический уровень предшествующего периода, – сглаженное значение предшествующего периода. Для константы сглаживания наиболее подходящими являются значения от 0, 2 до 0, 3. Эти значения показывают, что ошибка текущего прогноза установлена на уровне от 20 до 30 процентов ошибки предыдущего прогноза.

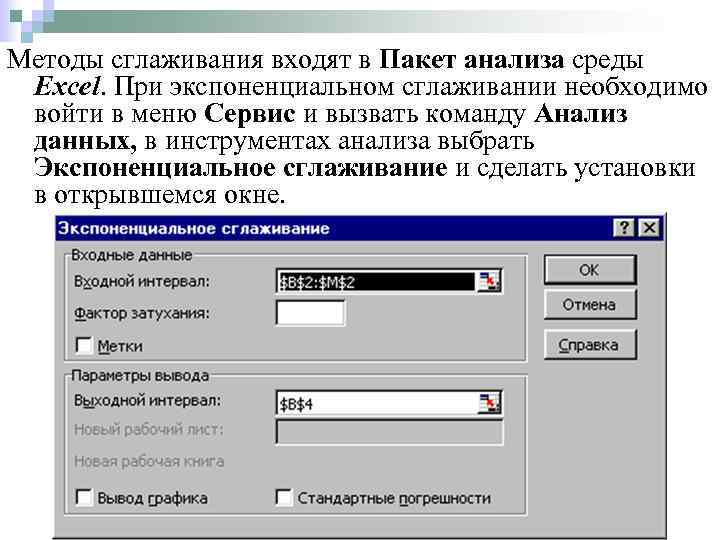Методы сглаживания входят в Пакет анализа среды Excel. При экспоненциальном сглаживании необходимо войти в меню Сервис и вызвать команду Анализ данных, в инструментах анализа выбрать Экспоненциальное сглаживание и сделать установки в открывшемся окне.

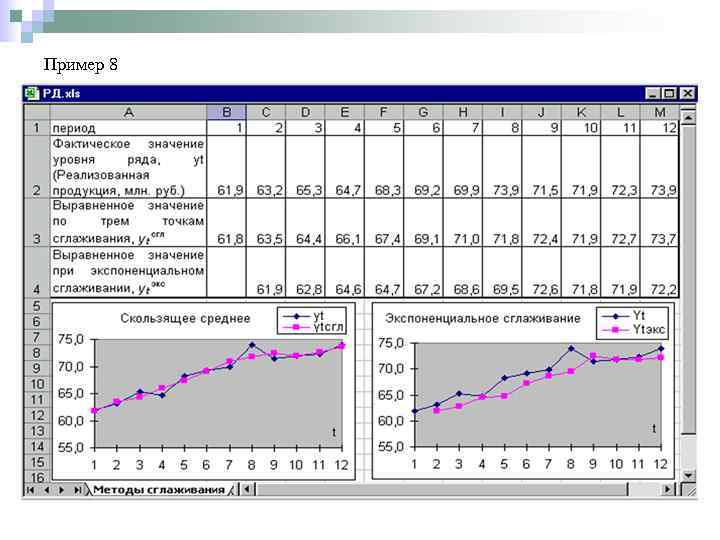Пример 8

9. 6. Аналитическое выравнивание. Прогнозирование тенденций развития с помощью моделей кривых роста

На практике для описания тенденции развития широко используются модели кривых роста, представляющие собой различные функции времени y=f(t). При таком подходе изменение исследуемого показателя связано лишь с течением времени; считается, что влияние других факторов несущественно или косвенно сказывается через фактор времени.

Прогнозирование на основе модели кривой роста базируется на экстраполяции, то есть на продлении в будущее тенденции, наблюдавшейся в прошлом. При этом предполагается, что n во временном ряду присутствует тренд, n характер развития показателя обладает свойствами инертности, n сложившаяся тенденция не должна претерпевать существенных изменений в течение периода упреждения.

Схема разработки прогнозов с использование кривых роста 1. Выбор одной или нескольких кривых, форма которых соответствует характеру изменения временного ряда 2. Оценка параметров выбранных кривых 3. Проверка адекватности выбранных кривых прогнозируемому процессу, оценка точности моделей и окончательный выбор кривой роста 4. Расчет точечного и интервального прогнозов

В настоящее время в литературе описано несколько десятков кривых роста. Модели кривых роста могут быть условно разделены на три класса в зависимости от того, какой тип динамики развития они хорошо описывают.

К первому классу относятся функции, используемые для описания процессов с монотонным характером тенденции развития и отсутствием пределов роста. Эти условия справедливы для многих экономических показателей, например, для большинства показателей промышленного производства в натуральном выражении.

Ко второму классу относятся кривые, описывающие процесс, который имеет предел роста в исследуемом периоде. С такими процессами часто сталкиваются n в демографии, n при изучении потребностей в товарах и услугах (в расчете на душу населения), n исследовании эффективности использования ресурсов и т. д. Функции, относящиеся ко второму классу, называются кривыми насыщения.

Если кривые насыщения имеют точки перегиба, то они относятся к третьему типу кривых роста – к Sобразным кривым. Эти кривые описывают два последовательных лавинообразных процесса (когда прирост зависит от уже достигнуто уровня): один с ускорением развития, другой – с замедлением. S-образные кривые находят применение n в демографических исследованиях, n в страховых расчетах, n при решении задач прогнозирования научнотехнического прогресса, n при определении спроса на новый вид продукции.

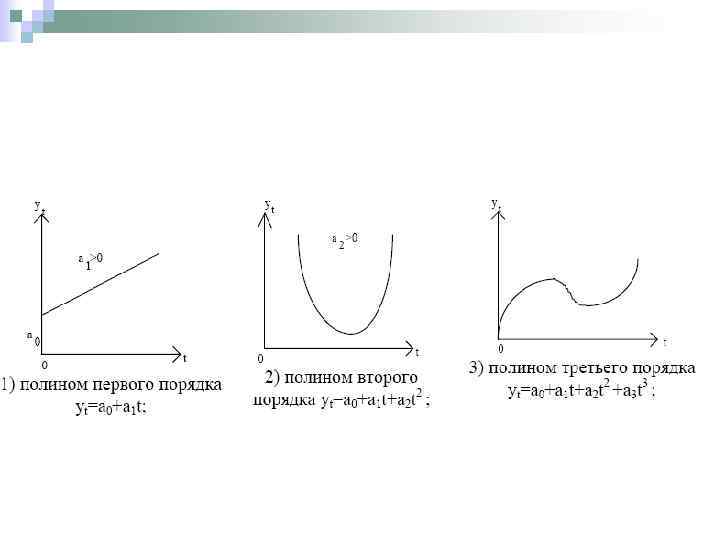
Среди кривых роста первого типа, прежде всего, следует выделить класс полиномов: где ai (i=0, 1, , p) – параметры многочлена; t – независимая переменная (время), t=1, 2, , n. Обычно в экономических исследованиях применяются полиномы не выше третьего порядка. Использовать для определения тренда полиномы высоких степеней нецелесообразно, поскольку полученные таким образом аппроксимирующие функции будут отражать случайные отклонения, что противоречит смыслу тенденции.

Оценка неизвестных параметров модели осуществляется следующими методами: n методом избранных точек, n методом наименьших расстояний, n методом наименьших квадратов (МНК). В большинстве расчетов используется метод наименьших квадратов, который обеспечивает наименьшую сумму квадратов отклонений фактических уровней от выровненных:

Для линейной зависимости параметр a 0 обычно интерпретации не имеет, но иногда его рассматривают, как обобщенный начальный уровень ряда; a 1 – сила связи, т. е. параметр, показывающий, насколько изменится результат при изменении времени на единицу. Таким образом, a 1 можно представить как постоянный теоретический абсолютный прирост.

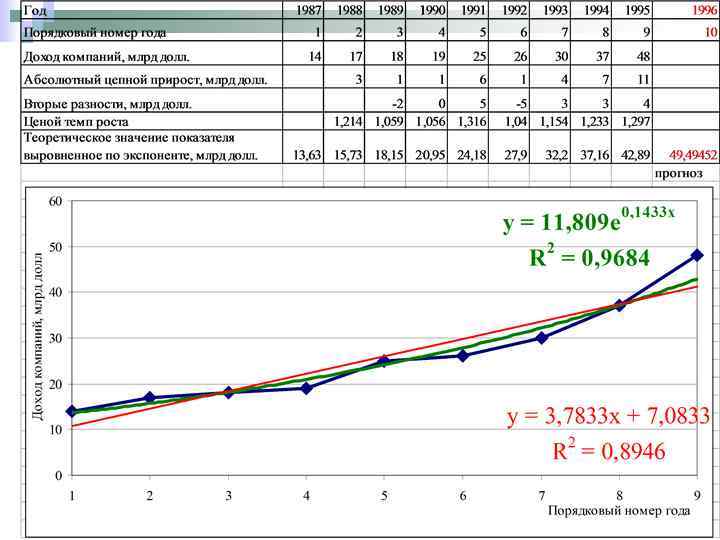
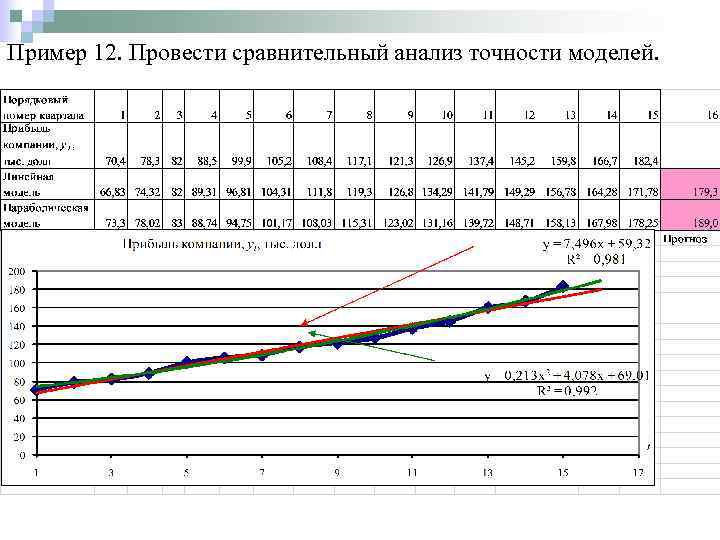
Пример 9. В таблице представлены квартальные данные о прибыли компании. Требуется рассчитать прогноз прибыли в следующем (16 -м) квартале, предположив, что тенденция может быть описана: а) линейной моделью б) параболической моделью

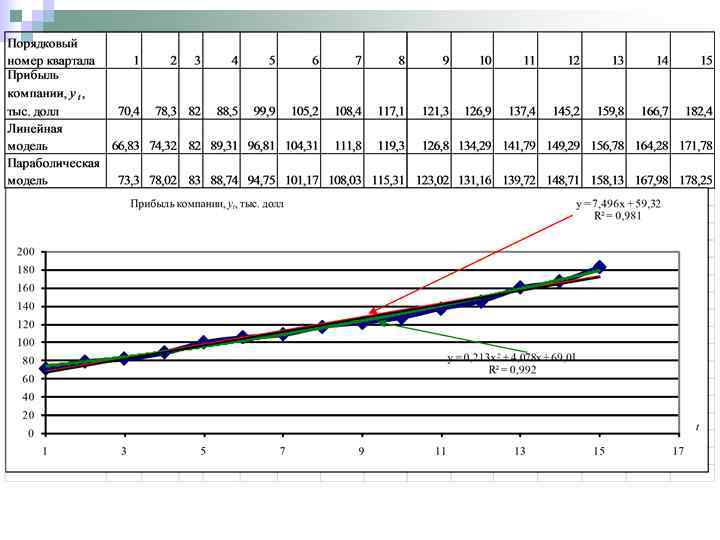
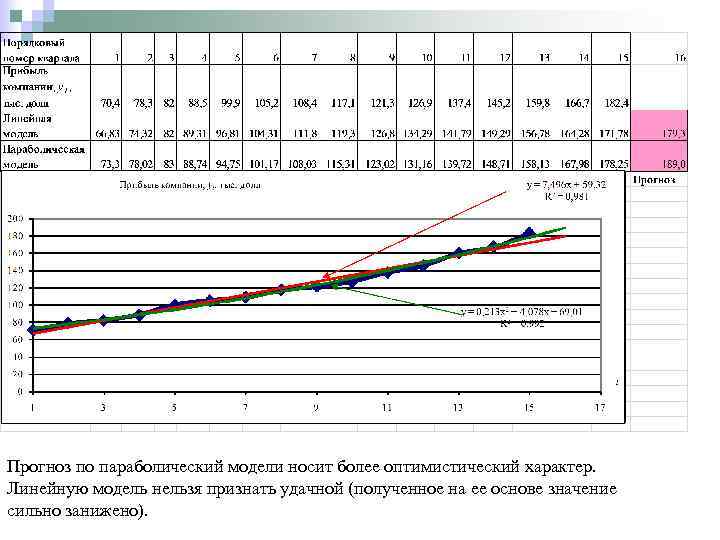Прогноз по параболический модели носит более оптимистический характер. Линейную модель нельзя признать удачной (полученное на ее основе значение сильно занижено).

n n Линейная зависимость выбирается в тех случаях, когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению. Параболическая зависимость используется, если абсолютные цепные приросты сами по себе обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют.

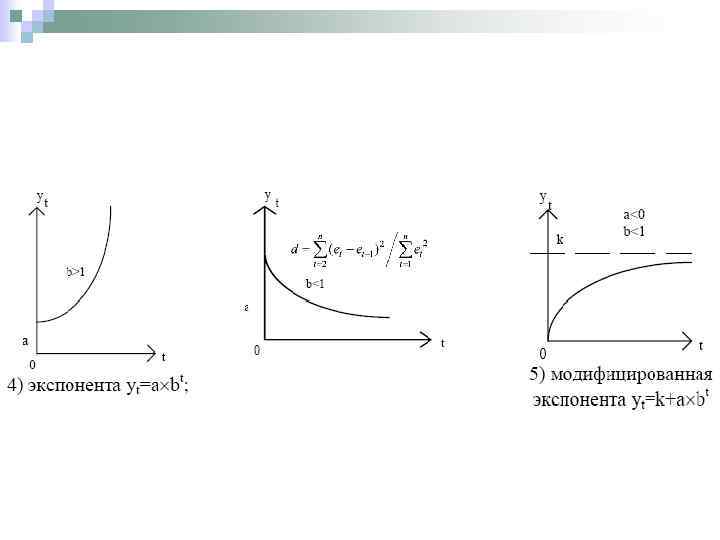
Класс экспоненциальных кривых также используется при моделировании и прогнозировании тенденции развития экономических показателей. Эти кривые хорошо описывают процессы, имеющие «лавинообразный» характер, когда прирост зависит от достигнутого уровня функции.

Простая показательная (экспоненциальная) кривая имеет вид: Параметр a характеризует начальные условия развития, а параметр b – постоянный темп роста. Действительно для экспоненциальной кривой цепной темп роста равен:

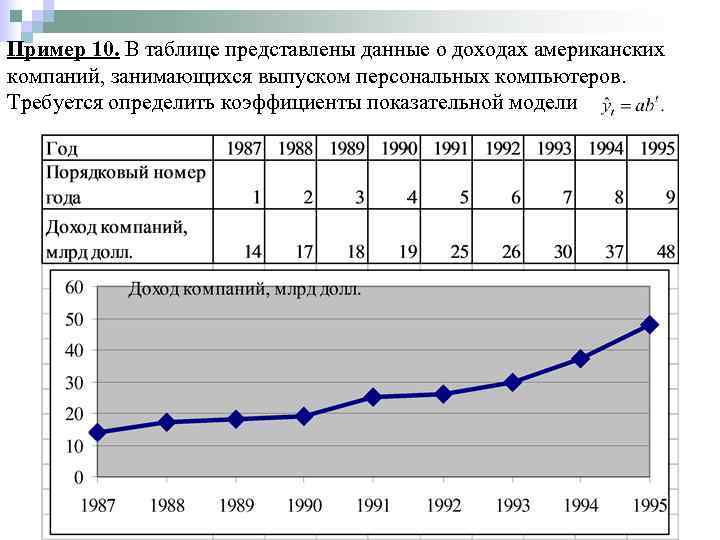Пример 10. В таблице представлены данные о доходах американских компаний, занимающихся выпуском персональных компьютеров. Требуется определить коэффициенты показательной модели

В Excel экспоненциальная кривая имеет вид: Цепной темп роста в этом случае также остается постоянным:

Экспоненциальные зависимости применяются, если в исходном временном ряду наблюдается либо более или менее постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста), либо, при отсутствии такого постоянства, – устойчивость в изменении показателей относительного роста (цепных темпов роста цепных же темпов роста, цепных коэффициентов роста цепных же коэффициентов или темпов роста и т. п. ).

Когда процесс характеризуется «насыщением» , его следует описывать при помощи кривой, имеющей отличную от нуля асимптоту. Примером такой кривой может служить модифицированная экспонента: где y=k является горизонтальной асимптотой. Если параметр а отрицателен, то асимптота находится выше кривой, если а положителен, то ниже. При решении экономический задач, чаще всего приходится иметь дело с кривой, у которой а<0, b<1. В этом случае рост уровней происходит с замедлением и стремится к некоторому пределу.

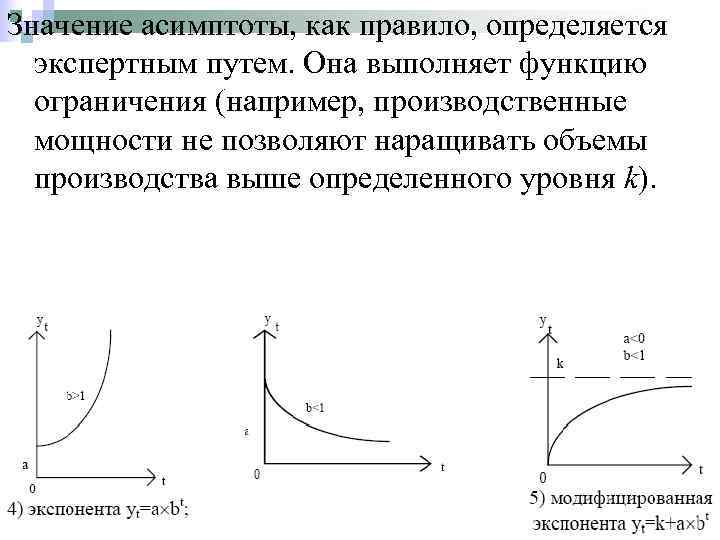Значение асимптоты, как правило, определяется экспертным путем. Она выполняет функцию ограничения (например, производственные мощности не позволяют наращивать объемы производства выше определенного уровня k).

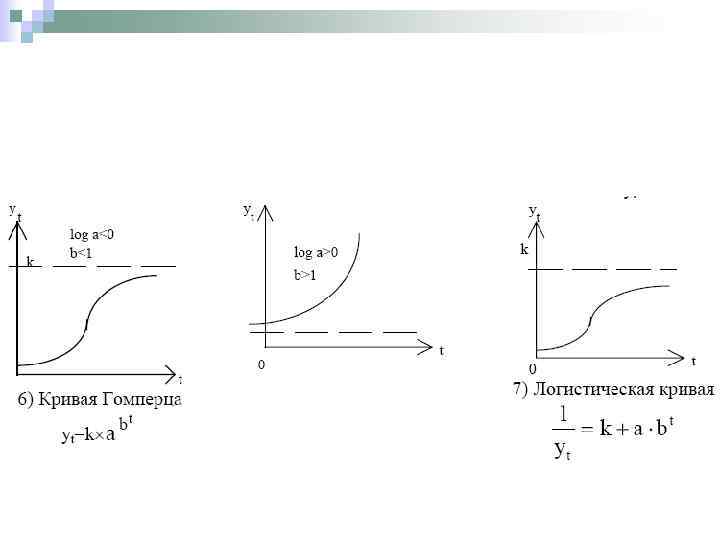
Если воздействие ограничивающего фактора начинает сказывать только после определенного момента (точки перегиба), до которого процесс развивался по некоторому экспоненциальному закону, то для выравнивания используются S-образные кривые. Наиболее известные из них: кривая Гомперца Логистическая кривая Перла-Рида

9. 7. Методы выбора кривых роста

Существует несколько практических подходов, облегчающих процесс выбора формы кривой роста. 1. Визуальный, опирающийся на графическое изображение временного ряда. Подбирают такую кривую роста, форма которой соответствует фактическому развитию процесса. Если на графике исходного ряда тенденция развития недостаточно четко просматривается, то можно провести некоторые стандартные преобразования ряда (например, сглаживание), а потом подобрать функцию, отвечающую графику преобразованного ряда.

2. Метод последовательных разностей, помогающий при выборе кривых параболического типа. Этот метод применим при выполнении предположения, что уровни временного ряда могут быть представлены в виде суммы: n систематической составляющей и n случайной компоненты, подчиненной нормальному закону распределения с математическим ожиданием, равным 0, и постоянной дисперсией. Метод предполагает вычисление первых, вторых и т. д. разностей уровней ряда: и т. д. Расчет ведется до тех пор, пока разности не будут примерно равными. Порядок разностей принимается за степень выравнивающего полинома.

3. Метод характеристик прироста. Процедура выбора кривых с использованием этого метода включает следующие шаги: n выравнивание ряда по скользящей средней; n определение средних приростов; n вычисление производных характеристик прироста. Для многих видов кривых были найдены такие преобразования приростов, которые линейно изменялись относительно t или были постоянны. В связи с этим исследование характеристик приростов часто оказывает существенную помощь при определении законов развития исходных временных рядов. Данный метод является более универсальным по сравнению с методом последовательных разностей.

4. Выбор формы кривой исходя из значений критерия, в качестве которого принимают сумму квадратов отклонений фактических значений уровня от расчетных, получаемых выравниванием. Из рассматриваемых кривых предпочтение будет отдано той, которой соответствует минимальное значение критерия, т. к. чем меньше значение критерия, тем ближе к кривой ложатся данные наблюдений. Следует учитывать, что за счет роста сложности кривой можно увеличить точность описания тренда в прошлом, однако доверительные интервалы при прогнозировании будут существенно шире, чем у более простых кривых при одинаковом периоде упреждения, например, за счет большего числа параметров.

9. 8. Доверительные интервалы прогноза. Оценка адекватности и точности моделей

9. 8. 1. Доверительные интервалы прогноза

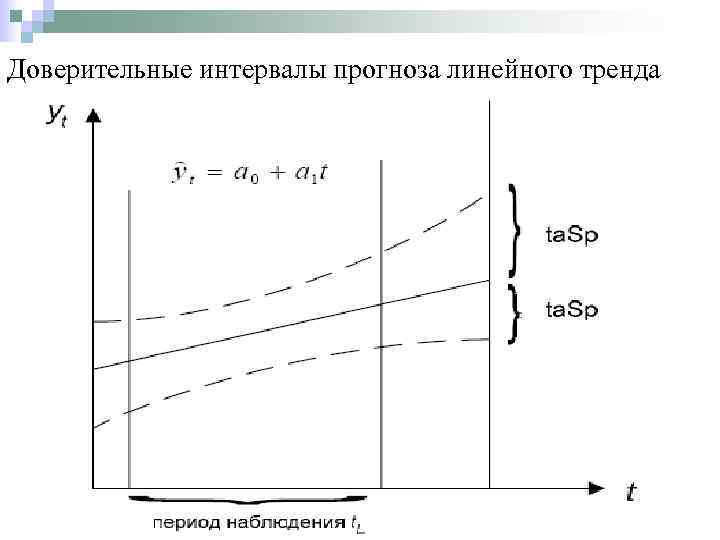
Заключительным этапом применения кривых роста является экстраполяция тенденции на базе выбранного уравнения. Прогнозные значения исследуемого показателя вычисляют путем подстановки в уравнение кривой значений времени t, соответствующих периоду упреждения. Полученный таким образом прогноз называют точечным, так как для каждого момента времени определяется только одно значение прогнозируемого показателя. На практике в дополнении к точечному прогнозу желательно определить границы возможного изменения прогнозируемого показателя, задать "вилку" возможных значений прогнозируемого показателя, т. е. вычислить прогноз интервальный.

Несовпадение фактических данных с точечным прогнозом, полученным путем экстраполяции тенденции по кривым роста, может быть вызвано: 1. субъективной ошибочностью выбора вида кривой; 2. погрешностью оценивания параметров кривых; 3. погрешностью, связанной с отклонением отдельных наблюдений от тренда, характеризующего некоторый средний уровень ряда на каждый момент времени. Погрешность, связанная со вторым и третьим источником, может быть отражена в виде доверительного интервала прогноза. Доверительный интервал, учитывающий неопределенность, связанную с положением тренда, и возможность отклонения от этого тренда, определяется в виде: где n - длина временного ряда; L -период упреждения; -точечный прогноз на момент n+L; t a- значение t-статистики Стьюдента; Sp- средняя квадратическая ошибка прогноза.

Дисперсия отклонений фактических наблюдений от расчетных определяется выражением: где yt- фактические значения уровней ряда, - расчетные значения уровней ряда, n- длина временного ряда, k - число оцениваемых параметров выравнивающей кривой.

Ширина доверительного интервала зависит от n уровня значимости, n периода упреждения, n среднего квадратического отклонения от тренда и n степени полинома. Чем выше степень полинома, тем шире доверительный интервал при одном и том же значении Sy, так как дисперсия уравнения тренда вычисляется как взвешенная сумма дисперсий соответствующих параметров уравнения

Доверительные интервалы прогноза линейного тренда

Доверительные интервалы прогнозов, полученных с использованием уравнения экспоненты, определяют аналогичным образом. Отличие состоит в том, что как при вычислении параметров кривой, так и при вычислении средней квадратической ошибки используют не сами значения уровней временного ряда, а их логарифмы. По такой же схеме могут быть определены доверительные интервалы для ряда кривых, имеющих асимптоты, в случае, если значение асимптоты известно (например, для модифицированной экспоненты).

9. 8. 2. Проверка адекватности выбранных моделей

Проверка адекватности выбранных моделей реальному процессу ( в частности, адекватности полученной кривой роста) строится на анализе случайной компоненты. Случайная остаточная компонента получается после выделения из исследуемого ряда систематической составляющей (тренда и периодической составляющей, если она присутствует во временном ряду). Предположим, что исходный временной ряд описывает процесс, не подверженный сезонным колебаниям, т. е. примем гипотезу об аддитивной модели ряда вида: yt = ut + e t. Тогда ряд остатков будет получен как отклонения фактических уровней временного ряда (yt) от выравненных, расчетных ( ): При использовании кривых роста вычисляют, подставляя в уравнения выбранных кривых соответствующие последовательные значения времени.

Принято считать, что модель адекватна описываемому процессу, если значения остаточной компоненты удовлетворяют свойствам случайности, независимости, а также случайная компонента подчиняется нормальному закону распределения. При правильном выборе вида тренда отклонения от него будут носить случайный характер. Это означает, что изменение остаточной случайной величины не связано с изменением времени. Таким образом, по выборке, полученной для всех моментов времени на изучаемом интервале, проверяется гипотеза о зависимости последовательности значений et от времени, или, что то же самое, о наличии тенденции в ее изменении. Для проверки данного свойства может быть использован один из критериев, например, критерий серий.

Если вид функции, описывающей систематическую составляющую, выбран неудачно, то последовательные значения ряда остатков могут не обладать свойствами независимости, т. к. они могут коррелировать между собой. В этом случае говорят, что имеет место автокорреляция ошибок. В условиях автокорреляции оценки параметров модели, полученные по методу наименьших квадратов, будут обладать свойствами несмещенности и состоятельности. В то же время эффективность этих оценок будет снижаться, а, следовательно, доверительные интервалы будут иметь мало смысла в силу своей ненадежности.

Наиболее распространенным приемом обнаружения автокорреляции является критерий Дарбина-Уотсона, который связан с гипотезой о существовании автокорреляции первого порядка, т. е. автокорреляции между соседними остаточными членами ряда. Значение этого критерия определяется по формуле: Можно показать, что величина d приближенно равна: где r 1 - коэффициент автокорреляции первого порядка (т. е. парный коэффициент корреляции между двумя рядами e 1, e 2, . . . , en-1 и e 2, e 3, . . . , en).

Из последней формулы видно, что если в значениях et имеется n сильная положительная автокорреляция (r 1 1), то величина d=0 , n в случае сильной отрицательной автокорреляции (r 1 -1) d=4. n При отсутствии автокорреляции (r 1 0) d=2. Для этого критерия найдены критические границы, позволяющие принять или отвергнуть гипотезу об отсутствии автокорреляции. Авторами критерия границы определены для 1, 2, 5 и 5% уровней значимости. Значения критерия Дарбина-Уотсона при 5% уровне значимости приведены в таблице. В этой таблице d 1 и d 2 соответственно нижняя и верхняя доверительные границы критерия Дарбина-Уотсона; k| - число переменных в модели; n длина временного ряда.

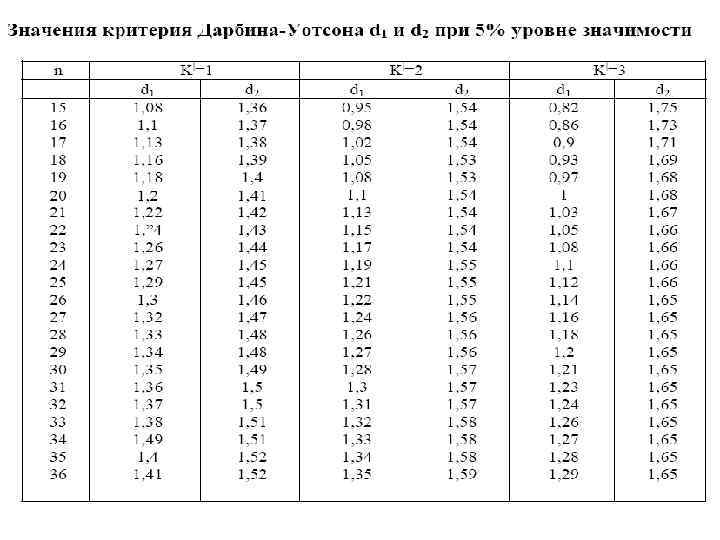
Применение на практике критерия Дарбина. Уотсона основано на сравнении величины d, рассчитанной по формуле, с теоретическими значениями d 1 и d 2, взятыми из таблицы. Отметим, что большинство программных пакетов статистической обработки данных осуществляет расчет этого критерия (например, ППП "Олимп", "Мезозавр", "Statistica" и др. ).

Выдвигается гипотеза H 0 об отсутствии автокорреляции остатков. Пусть альтернативная гипотеза состоит в наличии в остатках положительной автокорреляции первого порядка. Тогда при сравнении расчетного значения d (d<2) с d 1 и d 2 возможны следующие варианты: 1. если d < d 1, то гипотеза H 0 о независимости случайных отклонений (отсутствие автокорреляции) отвергается c вероятностью ошибки равной в пользу гипотезы о положительной автокорреляции; 2. Если d > d 2, то гипотеза H 0 о независимости случайных отклонений не отвергается; 3. Если d 1 d d 2, то нет достаточных оснований для принятия решений, т. е. величина попадает в область "неопределенности". Рассмотренные варианты относятся к случаю, когда в остатках имеется положительная автокорреляция.

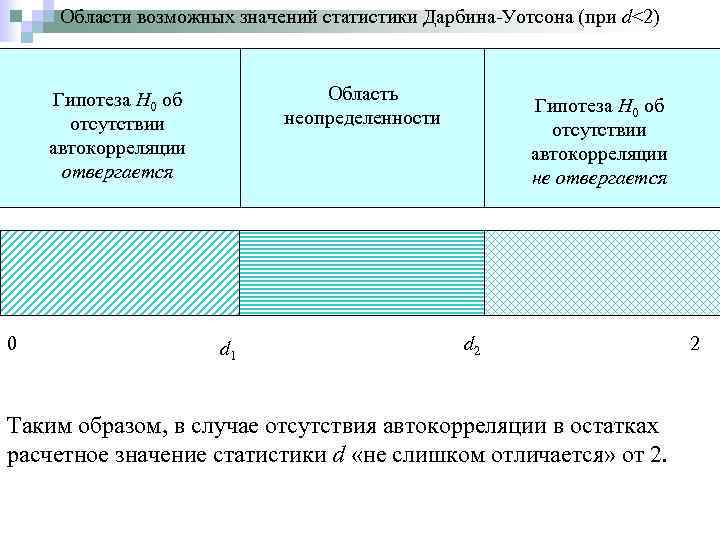Области возможных значений статистики Дарбина-Уотсона (при d<2) Область неопределенности Гипотеза Н 0 об отсутствии автокорреляции отвергается 0 d 1 Гипотеза Н 0 об отсутствии автокорреляции не отвергается d 2 Таким образом, в случае отсутствия автокорреляции в остатках расчетное значение статистики d «не слишком отличается» от 2. 2

Когда расчетное значение d >2, то можно говорить о том, что в et существует отрицательная автокорреляция. Для проверки отрицательной автокорреляции с критическими значениями d 1 и d 2 сравнивается не сам коэффициент d, а 4 -d. При этом возможны следующие варианты (d<2): 1. если 4 -d < d 1, то гипотеза H 0 об отсутствие автокорреляции отвергается c вероятностью ошибки равной в пользу гипотезы о отрицательной автокорреляции; 2. Если 4 - d > d 2, то гипотеза H 0 о независимости случайных отклонений не отвергается; 3. Если d 1 4 -d d 2, то нельзя сделать определенный вывод по имеющимся исходным данным.

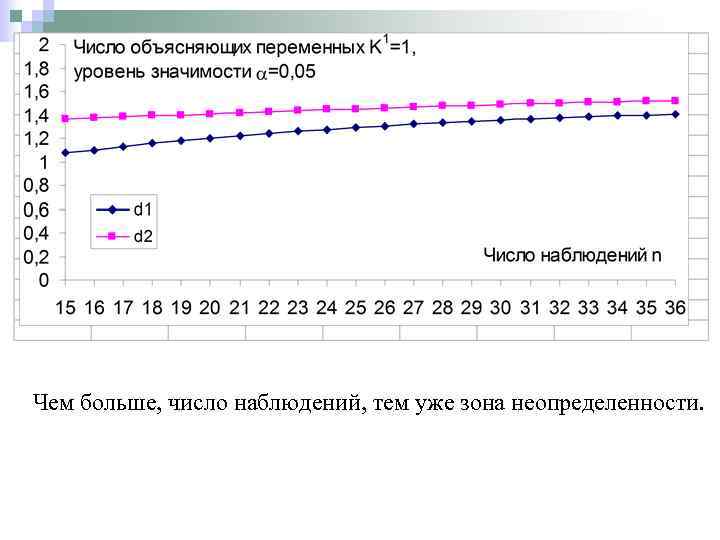Чем больше, число наблюдений, тем уже зона неопределенности.

Укрупненная схема применения критерия Дарбина-Уотсона 1. Определение коэффициентов модели и вычисление остатков 2. Расчет статистики Дарбина-Уотсона по формуле 3. Выбор табличных граничных значений статистики d 1 и d 2 в зависимости от значений параметров: - уровень значимости, k – число объясняющих переменных, n – число наблюдений. 4. Определение области, в которую попадает вычисленное значение статистики Дарбина-Уотсона

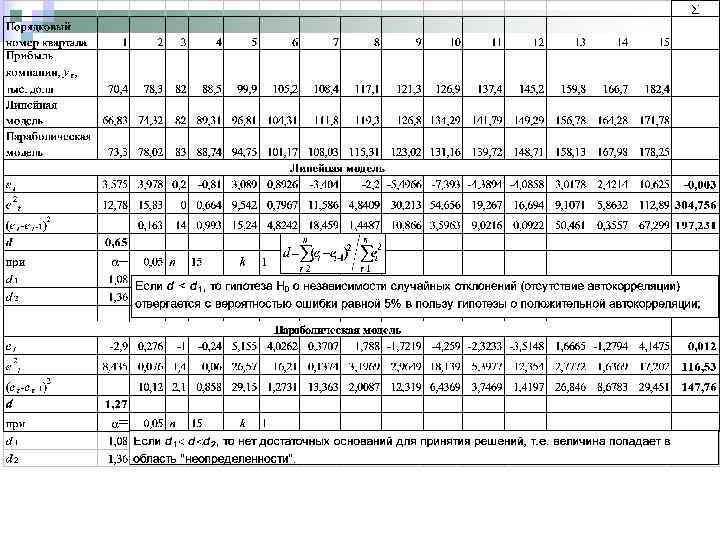
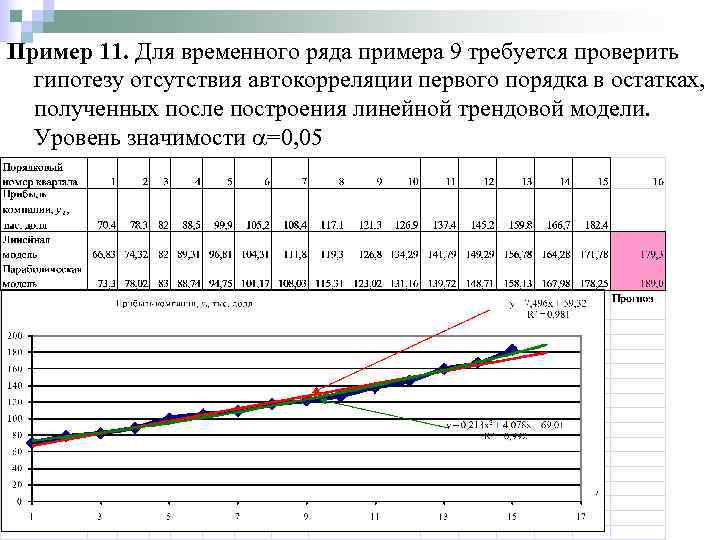Пример 11. Для временного ряда примера 9 требуется проверить гипотезу отсутствия автокорреляции первого порядка в остатках, полученных после построения линейной трендовой модели. Уровень значимости =0, 05

9. 8. 3. Оценка точности выбранных моделей прогнозирования

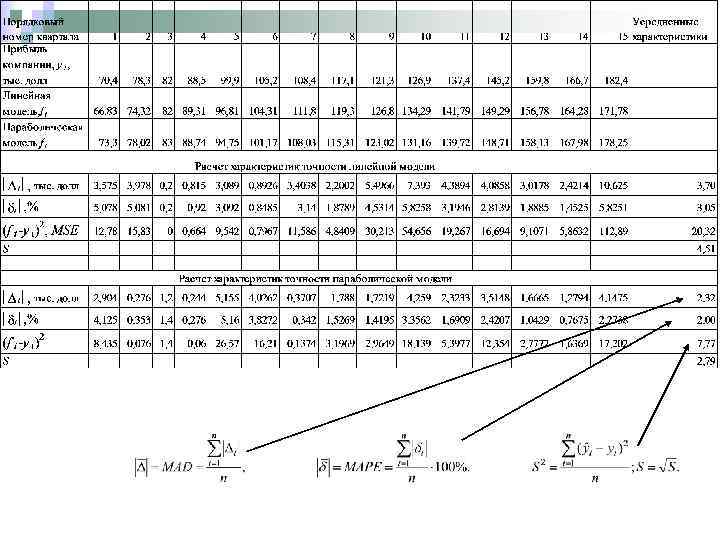
Важнейшими характеристиками качества модели, выбранной для прогнозирования, являются показатели ее точности. Они описывают величины случайных ошибок, полученных при использовании модели. Таким образом, чтобы судить о качестве выбранной модели, необходимо проанализировать систему показателей, характеризующих как адекватность модели, так и ее точность. О точности прогноза можно судить по величине ошибки (погрешности) прогноза. Ошибка прогноза - величина, характеризующая расхождение между фактическим и прогнозным значением показателя. Для оценки точности моделей прогнозирования используются следующие показатели.

1. Абсолютная ошибка прогноза определяется по формуле: где - прогнозное значение показателя, yt - фактическое значение. Эта характеристика имеет ту же размерность, что и прогнозируемый показатель и зависит от масштаба измерения уровней временного ряда. При расчете обобщающих показателей точности модели используют характеристику, полученную усреднением модулей абсолютных отклонений (Mean Absolute Derivation, MAD) : где n – число уровней временного ряда, для которых определяется прогнозное значение.

2. На практике широко используется относительная ошибка прогноза, выраженная в процентах относительно фактического значения показателя: Если ошибка больше нуля, то это свидетельствует о «завышенной» прогнозной оценке, если – меньше, то прогноз был занижен. Усредненная относительная ошибка (Mean Absolute Percentage Error, MAPE) используется для сравнения точности прогнозов разнородных объектов прогнозирования.

Высокая точность прогноза Точность можно признать хорошей Удовлетворительная точность Однако такая универсальность, не учитывающая специфики временных рядов и прогнозных расчетов, делает этот подход достаточно «механистическим» .

Иногда используется характеристика называемая Mean Percentage Error (MPE), отличающаяся от MAPE отсутствием модуля. Значение этой характеристики может указывать на наличие систематического смещения в прогнозных оценках.

3. На практике при проведении сравнительной оценки моделей могут использоваться такие характеристики качества как дисперсия (S 2) или среднеквадратическая ошибка прогноза (S): Чем меньше значения этих характеристик, тем выше точность модели. О точности модели нельзя судить по одному значению ошибки прогноза. О качестве применяемых моделей можно судить лишь по совокупности сопоставлений прогнозных значений с фактическими.

4. Простой мерой качества прогнозов может стать - относительное число случаев, когда фактическое значение охватывалось интервальным прогнозом: где р- число прогнозов, подтвержденных фактическими данными; qчисло прогнозов, не подтвержденных фактическими данными. Когда все прогнозы подтверждаются, q=0 и =1. Если же все прогнозы не подтвердились, то р=0 и =0. Отметим, что сопоставление коэффициентов для разных моделей может иметь смысл при условии, что доверительные вероятности приняты одинаковыми.

5. В Excel для оценка качества прогнозов используется коэффициент достоверности аппроксимации R 2. Чем ближе R 2 к 1, тем точнее прогноз. Межгрупповая дисперсия Общая дисперсия

Пример 12. Провести сравнительный анализ точности моделей.

9. 9. Прогнозирование сезонных колебаний

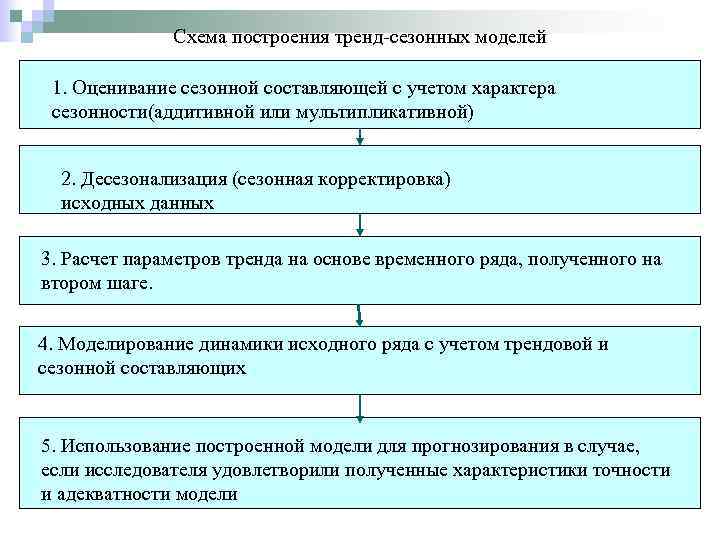Схема построения тренд-сезонных моделей 1. Оценивание сезонной составляющей с учетом характера сезонности(аддитивной или мультипликативной) 2. Десезонализация (сезонная корректировка) исходных данных 3. Расчет параметров тренда на основе временного ряда, полученного на втором шаге. 4. Моделирование динамики исходного ряда с учетом трендовой и сезонной составляющих 5. Использование построенной модели для прогнозирования в случае, если исследователя удовлетворили полученные характеристики точности и адекватности модели

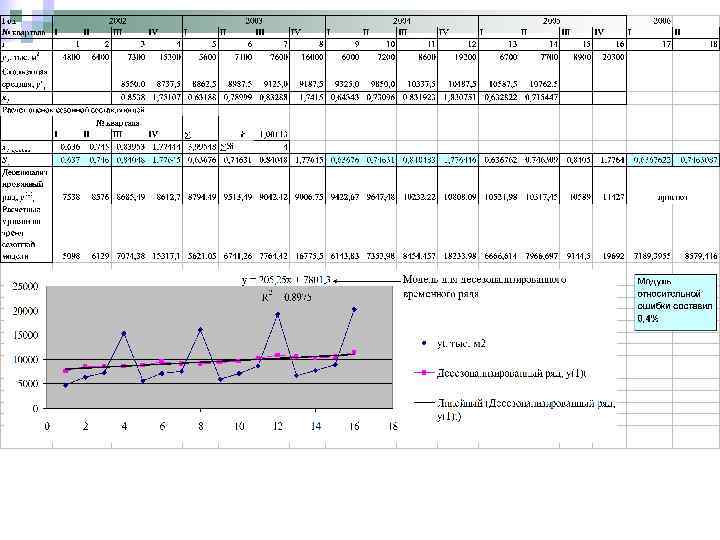
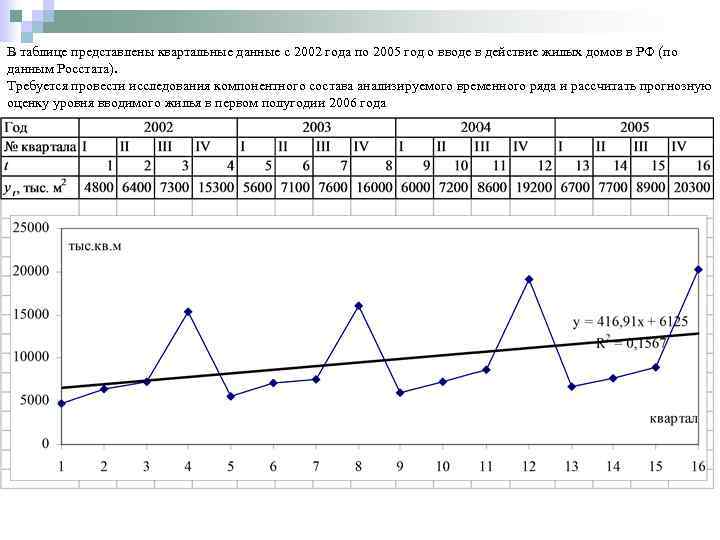В таблице представлены квартальные данные с 2002 года по 2005 год о вводе в действие жилых домов в РФ (по данным Росстата). Требуется провести исследования компонентного состава анализируемого временного ряда и рассчитать прогнозную оценку уровня вводимого жилья в первом полугодии 2006 года

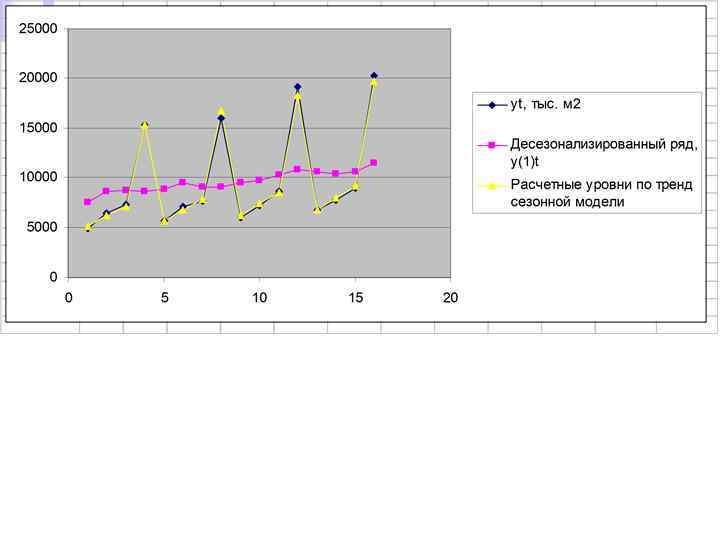
Так как амплитуда колебаний изменяется с течением времени (увеличивается с ростом тренда), то для описания динамики временного ряда можно предположить модель с мультипликативной сезонностью.

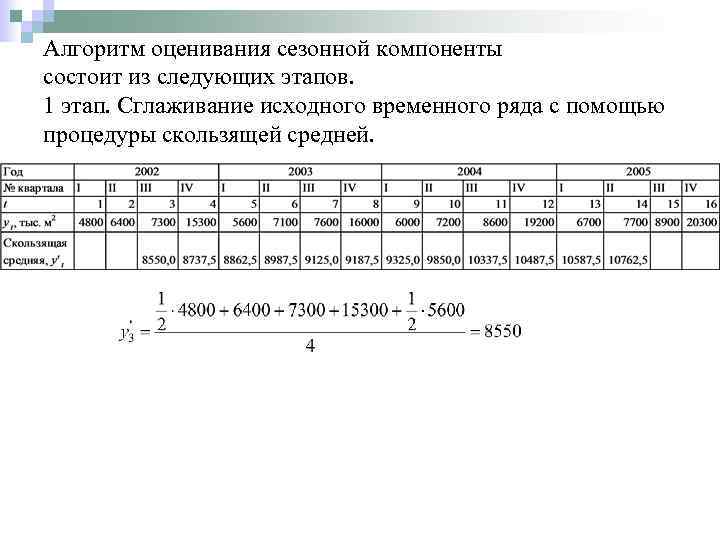Алгоритм оценивания сезонной компоненты состоит из следующих этапов. 1 этап. Сглаживание исходного временного ряда с помощью процедуры скользящей средней.

2. Вычисление уровней временного ряда xt, представляющих собой отношения/разности фактических уровней yt и сглаженных значений y‘t, полученных на предыдущем шаге (соответственно для случая мультипликативной/аддитивной сезонности). для мультипликативной сезонности для аддитивной модели Уровни xt отражают влияние случайных факторов и сезонности

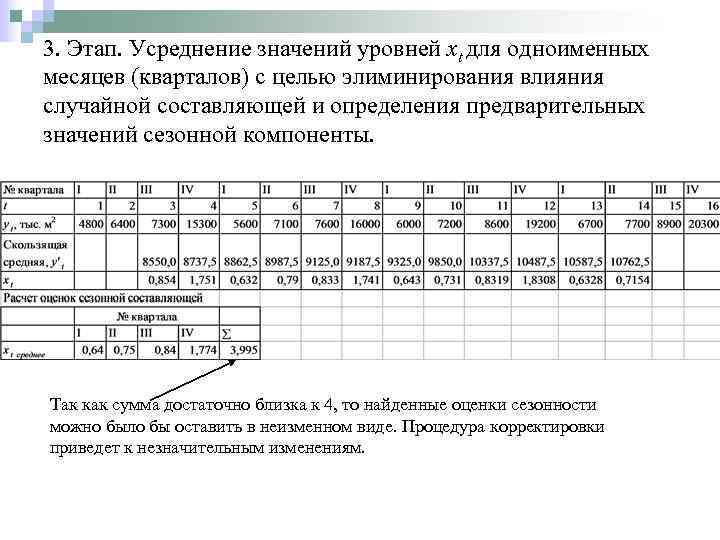3. Этап. Усреднение значений уровней xt для одноименных месяцев (кварталов) с целью элиминирования влияния случайной составляющей и определения предварительных значений сезонной компоненты. Так как сумма достаточно близка к 4, то найденные оценки сезонности можно было бы оставить в неизменном виде. Процедура корректировки приведет к незначительным изменениям.

4. Проведение корректировки первоначальных значений сезонной составляющей с учетом мультипликативного или аддитивного характера сезонности для того, чтобы суммарное воздействие сезонности на динамику было нейтральным. Коэффициент сезонности: n для мультипликативной сезонности n для аддитивной модели m – число фаз в полном сезонном цикле, m=12 для рядов месячной динамики и m=4 для квартальных данных.

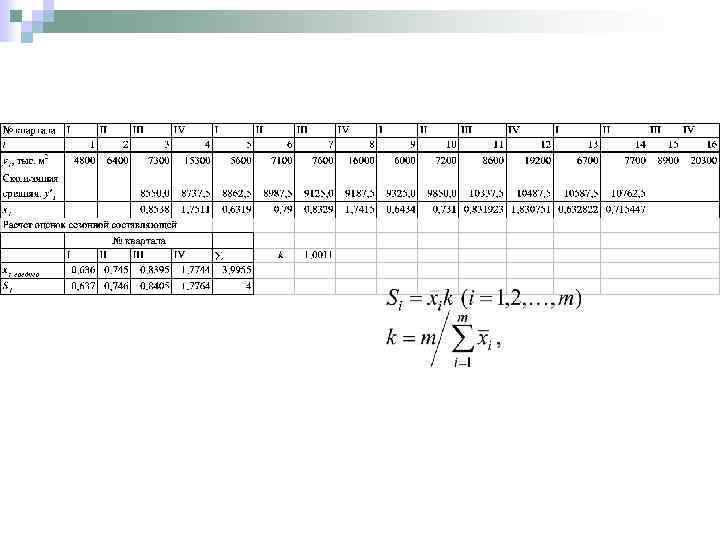
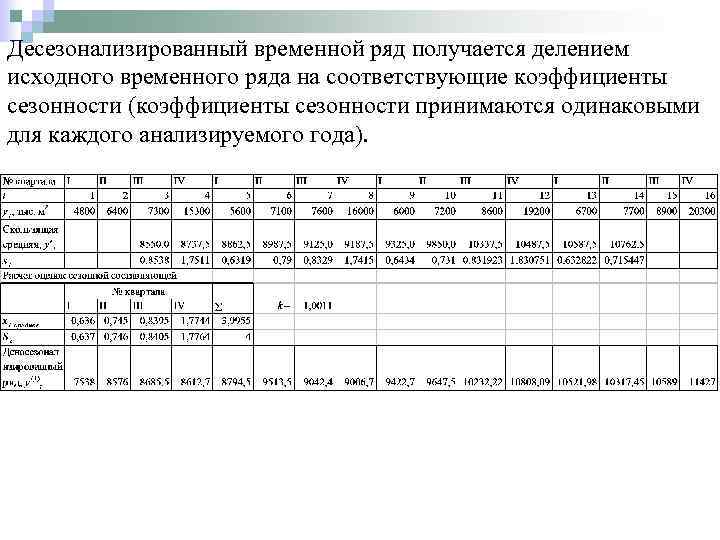Десезонализированный временной ряд получается делением исходного временного ряда на соответствующие коэффициенты сезонности (коэффициенты сезонности принимаются одинаковыми для каждого анализируемого года).

n n Добавить пример с интервальным прогнозом