9 -2 Piecewise Functions Objectives Write and graph

9 -2 Piecewise Functions Objectives Write and graph piecewise functions. Use piecewise functions to describe realworld situations. Vocabulary piecewise function Holt Algebra 2 step function

9 -2 Piecewise Functions Notes #1 -2 1. A) Create a table for the two pieces B)Graph the function. g(x) = – 3 x if x < 2 x+3 if x ≥ 2 2. Write and graph a piecewise function for the following situation. A house painter charges $12 per hour for the first 40 hours he works, time and a half for the 10 hours after that, and double time for all hours after that. How much does he earn for a 70 -hour week? Holt Algebra 2

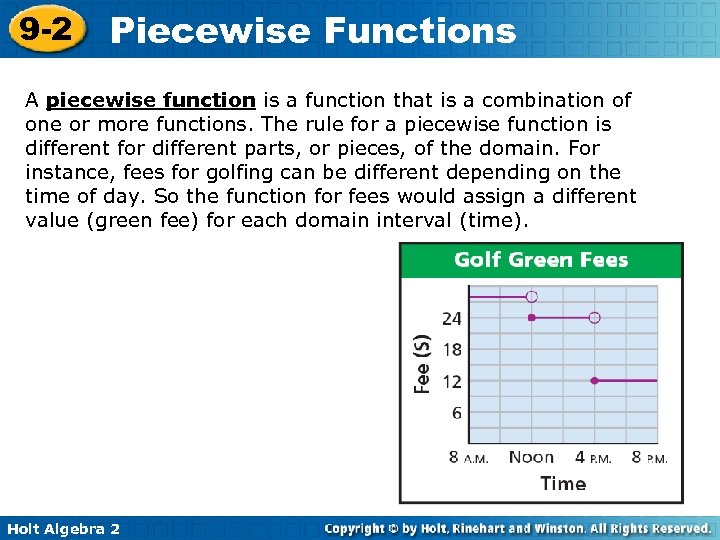
9 -2 Piecewise Functions A piecewise function is a function that is a combination of one or more functions. The rule for a piecewise function is different for different parts, or pieces, of the domain. For instance, fees for golfing can be different depending on the time of day. So the function for fees would assign a different value (green fee) for each domain interval (time). Holt Algebra 2

9 -2 Piecewise Functions Remember! When using interval notation, square brackets [ ] indicate an included endpoint, and parentheses ( ) indicate an excluded endpoint. (Lesson 1 -1) Holt Algebra 2

9 -2 Piecewise Functions Example 1: Consumer Application Create a table and a verbal description to represent the graph. Step 1 Create a table Because the endpoints of each segment of the graph identify the intervals of the domain, use the endpoints and points close to them as the domain values in the table. Holt Algebra 2

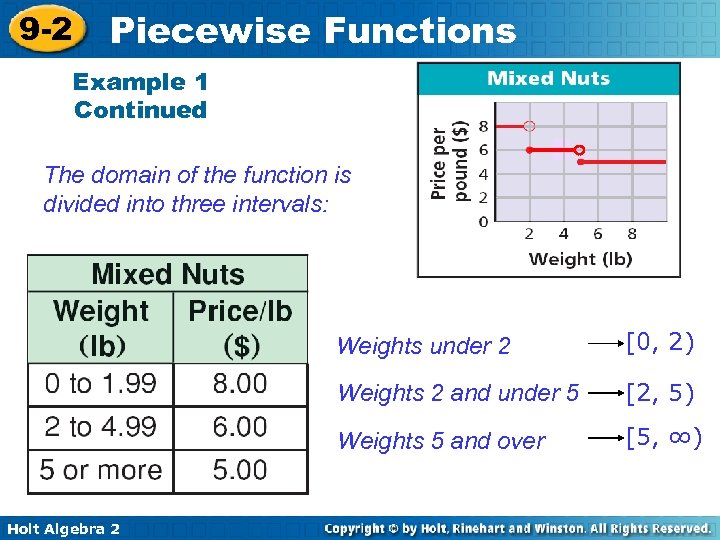
9 -2 Piecewise Functions Example 1 Continued The domain of the function is divided into three intervals: Weights under 2 Weights 2 and under 5 [2, 5) Weights 5 and over Holt Algebra 2 [0, 2) [5, ∞)

9 -2 Piecewise Functions Example 1 Continued Step 2 Write a verbal description. Mixed nuts cost $8. 00 per pound for less than 2 lb, $6. 00 per pound for 2 lb or more and less than 5 lb, and $5. 00 per pound for 5 or more pounds. Holt Algebra 2

9 -2 Piecewise Functions A piecewise function that is constant for each interval of its domain, such as the ticket price function, is called a step function. You can describe piecewise functions with a function rule. The rule for the movie ticket prices from Example 1 on page 662 is shown. Holt Algebra 2

9 -2 Piecewise Functions Read this as “f of x is 5 if x is greater than 0 and less than 13, 9 if x is greater than or equal to 13 and less than 55, and 6. 5 if x is greater than or equal to 55. ” Holt Algebra 2

9 -2 Piecewise Functions Example 2 A: Evaluating a Piecewise Function Evaluate each piecewise function for x = – 1 and x = 4. 2 x + 1 h(x) = if x ≤ 2 x 2 – 4 if x > 2 h(– 1) = 2(– 1) + 1 = – 1 h(4) = 42 – 4 = 12 Holt Algebra 2 Because – 1 ≤ 2, use the rule for x ≤ 2. Because 4 > 2, use the rule for x > 2.

9 -2 Piecewise Functions Example 2 B Evaluate each piecewise function for x = – 1 and x = 3. 12 if x < – 3 f(x) = 15 if – 3 ≤ x < 6 20 if x ≥ 6 f(– 1) = 15 f(3) = 15 Holt Algebra 2 Because – 3 ≤ – 1 < 6, use the rule for – 3 ≤ x < 6. Because – 3 ≤ 3 < 6, use the rule for – 3 ≤ x < 6.

9 -2 Piecewise Functions You can graph a piecewise function by graphing each piece of the function. Holt Algebra 2

9 -2 Piecewise Functions Example 3 A: Graphing Piecewise Functions Graph each function. g(x) = 1 4 x+3 – 2 x + 3 if x < 0 if x ≥ 0 The function is composed of two linear pieces that will be represented by two rays. Because the domain is divided by x = 0, evaluate both branches of the function at x = 0. Holt Algebra 2

9 -2 Piecewise Functions Example 3 A Continued For the first branch, the function is 3 when x = 0, so plot the point (0, 3) with an open circle and draw a ray with the slope 0. 25 to the left. For the second branch, the function is 3 when x = 0, so plot the point (0, 3) with a solid dot and draw a ray with the slope of – 2 to the right. Holt Algebra 2 ● O

9 -2 Piecewise Functions Example 3 B: Graphing Piecewise Functions Graph each function. x 2 – 3 g(x) = 1 2 x– 3 (x – 4)2 – 1 if x < 0 if 0 ≤ x < 4 if x ≥ 4 The function is composed of one linear piece and two quadratic pieces. The domain is divided at x = 0 and at x = 4. Holt Algebra 2

9 -2 Piecewise Functions Example 3 B Continued No circle is required at (0, – 3) and (4, – 1) because the function is connected at those points. Holt Algebra 2

9 -2 Piecewise Functions Notice that piecewise functions are not necessarily continuous, meaning that the graph of the function may have breaks or gaps. To write the rule for a piecewise function, determine where the domain is divided and write a separate rule for each piece. Combine the pieces by using the correct notation. Remember! The distance formula d = rt can be arranged to find rates: r = Holt Algebra 2 d t .

9 -2 Piecewise Functions Example 4: Sports Application Jennifer is completing a 15. 5 -mile triathlon. She swims 0. 5 mile in 30 minutes, bicycles 12 miles in 1 hour, and runs 3 miles in 30 minutes. Sketch a graph of Jennifer’s distance versus time. Then write a piecewise function for the graph. Holt Algebra 2

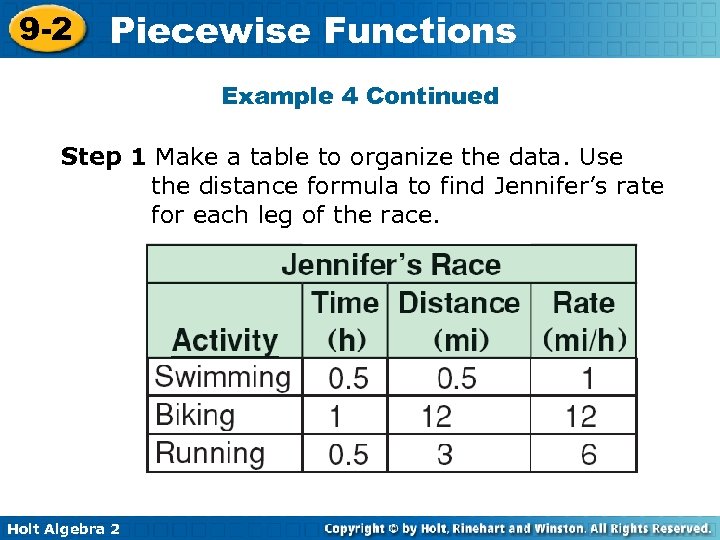
9 -2 Piecewise Functions Example 4 Continued Step 1 Make a table to organize the data. Use the distance formula to find Jennifer’s rate for each leg of the race. Holt Algebra 2

9 -2 Piecewise Functions Example 4 Continued Step 2 Because time is the independent variable, determine the intervals for the function. Swimming: 0 ≤ t ≤ 0. 5 She swims for half an hour. Biking: 0. 5 < t ≤ 1. 5 She bikes for the next hour. Running: 1. 5 < t ≤ 2 She runs the final half hour. Holt Algebra 2

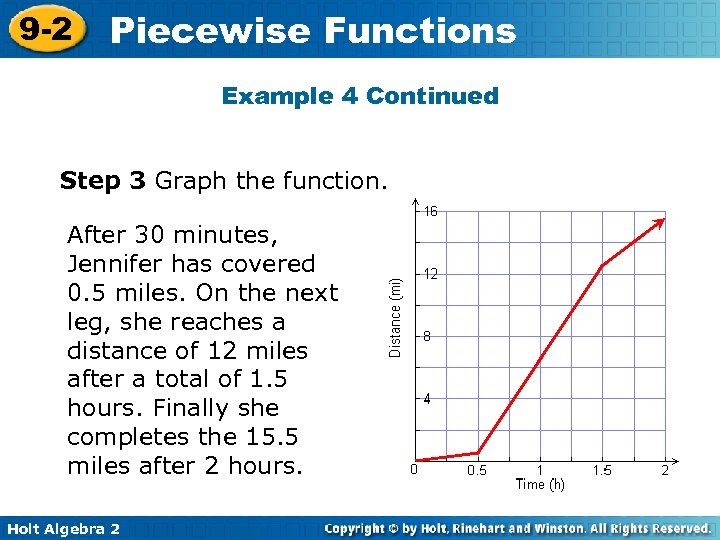
9 -2 Piecewise Functions Example 4 Continued Step 3 Graph the function. After 30 minutes, Jennifer has covered 0. 5 miles. On the next leg, she reaches a distance of 12 miles after a total of 1. 5 hours. Finally she completes the 15. 5 miles after 2 hours. Holt Algebra 2

9 -2 Piecewise Functions Example 4 Continued Step 4 Write a linear function for each leg. Swimming: d = t Use m = 0. 5 and (0, 0). Biking: d = 12 t – 5. 5 Use m = 12 and (0. 5, 0. 5). Use m = 6 and (1. 5, 12. 5). Running: d = 6 t + 3. 5 The function rule is d(t) = t if 0 ≤ t ≤ 0. 5 12 t – 5. 5 if 0. 5 < t ≤ 1. 5 6 t + 3. 5 Holt Algebra 2 if 1. 5 < t ≤ 2

9 -2 Piecewise Functions Notes #1 1. A) Create a table for the two pieces B)Graph the function. g(x) = – 3 x if x < 2 x+3 if x ≥ 2 The function is composed of two linear pieces. The domain is divided at x = 2. Holt Algebra 2

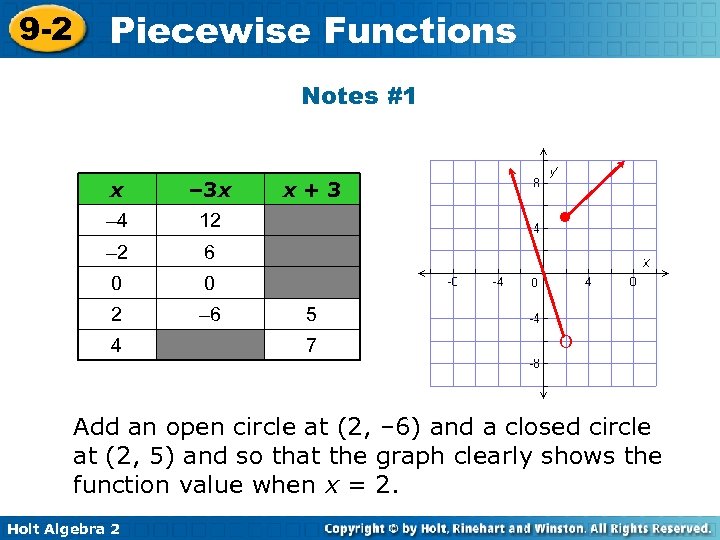
9 -2 Piecewise Functions Notes #1 x – 3 x – 4 12 – 2 6 0 0 2 – 6 4 x+3 ● 5 7 O Add an open circle at (2, – 6) and a closed circle at (2, 5) and so that the graph clearly shows the function value when x = 2. Holt Algebra 2

9 -2 Piecewise Functions Notes #2 2. Write and graph a piecewise function for the following situation. A house painter charges $12 per hour for the first 40 hours he works, time and a half for the 10 hours after that, and double time for all hours after that. How much does he earn for a 70 -hour week? Holt Algebra 2