9 -1 Estimation and Confidence Intervals Copyright

9 -1 Estimation and Confidence Intervals Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

9 -2 When you have completed this chapter, you will be able to: Define a point estimator, a point estimate, and desirable properties of a point estimator such as unbiasedness, efficiency, and consistency. Define an interval estimator and an interval estimate Define a confidence interval, confidence level, margin of error, and a confidence interval estimate Construct a confidence interval for the population mean when the population standard deviation is known Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

9 -3 Construct a confidence interval for the population variance when the population is normally distributed Construct a confidence interval for the population mean when the population is normally distributed and the population standard deviation is unknown Construct a confidence interval for a population proportion Determine the sample size for attribute and variable sampling Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Terminology 9 -4 Point Estimate …is a single value (statistic) used to estimate a population value (parameter) Interval Estimate …states the range within which a population parameter probably lies Confidence Interval …is a range of values within which the population parameter is expected to occur Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Desirable properties of a point estimator 9 -5 • efficient … possible values are concentrated close to the value of the parameter • consistent …values are distributed evenly on both sides of the value of the parameter • unbiased …unbiased when the expected value equals the value of the population parameter being estimated. Otherwise, it is biased! Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Terminology Standard error of the sample mean …is the standard deviation of the sampling distribution of the sample means x x It is computed by = n …is the symbol for the standard error of the sample mean …is the standard deviation of the population n …is the size of the sample Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 -6

Standard Error of the Means If is not known and n > 30, the standard deviation of the sample(s) is used to approximate the population standard deviation s = s Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. x Computed by… n 9 -7

9 -8 …that determine the width of a confidence interval are: 1. The sample size, n 2. The variability in the population, usually estimated by s 3. The desired level of confidence Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Constructing Confidence Intervals 9 -9 IN GENERAL, A confidence interval for a mean is computed by: ± zα/2 s n x Interpreting… Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Interpreting Confidence Intervals 9 - 10 The Globe Suppose that you read that “…the average selling price of a family home in York Region is $200 000 +/- $15000 at 95% confidence!” This means…what? Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Interpreting Confidence Intervals The Globe “…the average selling price of a family home in York Region is $200 000 +/$15 000 at 95% confidence!” 9 - 11 In statistical terms, this means: …that we are 95% sure that the interval estimate obtained contains the value of the population mean. Lower confidence limit is $185 000 ($200 000 - $15 000) Upper confidence limit is $215 000 ($200 000 + $15 000) Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. Also…

Interpreting Confidence Intervals The Globe “…the mean time to sell a family home in York Region is 40 days. 9 - 12 Your newspaper also reports that… You select a random sample of 36 homes sold during the past year, and determine a 90% confidence interval estimate for the population mean to be (31 -39) days. Do your sample results support the paper’s claim? Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Interpreting Confidence Intervals 9 - 13 Lower confidence limit You select a is 31 days random sample Upper confidence limit of 36 homes is 39 days sold during Our evidence does not support the past year, statement made by the newspaper, and determine a i. e. , the population mean is not 40 days, 90% confidence when using a 90% interval estimate for the population There is a 10% chance (100%-90%) that the interval estimate does mean to be not contain the value of (31 -39) days. the population mean! Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

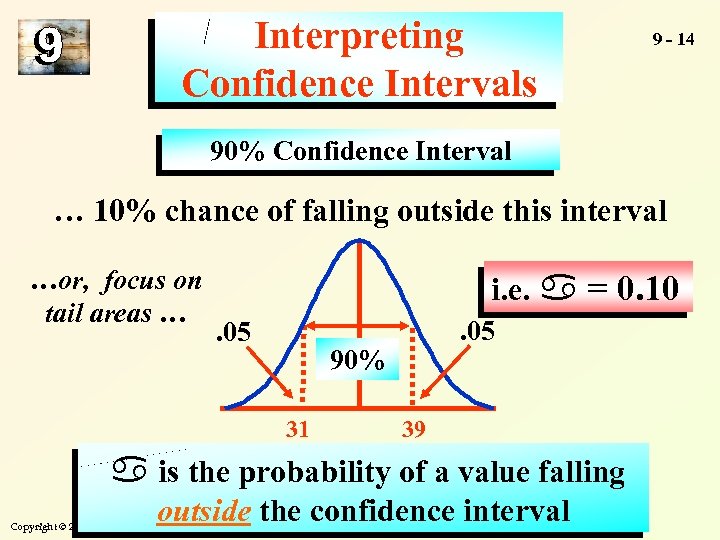Interpreting Confidence Intervals 9 - 14 90% Confidence Interval … 10% chance of falling outside this interval …or, focus on tail areas … i. e. = 0. 10. 05 90% 31 39 is the probability of a value falling outside the confidence interval Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

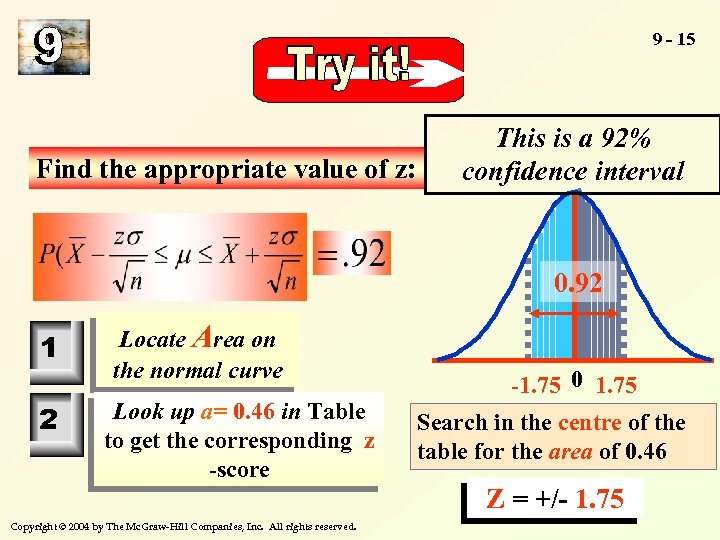9 - 15 Find the appropriate value of z: This is a 92% confidence interval 0. 92 1 2 Locate Area on the normal curve Look up a= 0. 46 in Table to get the corresponding z -score -1. 75 0 1. 75 Search in the centre of the table for the area of 0. 46 Z = +/- 1. 75 Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Constructing Confidence Intervals x Common Confidence Intervals ± zα/2 95% C. I. for the mean: 99% C. I. for the mean: Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 16 s n Also, 95% ofof About 95% the sample means for the constructed a intervals will specified sample size will lie within contain the 1. 96 standard parameter being deviations of the estimated. hypothesized population mean.

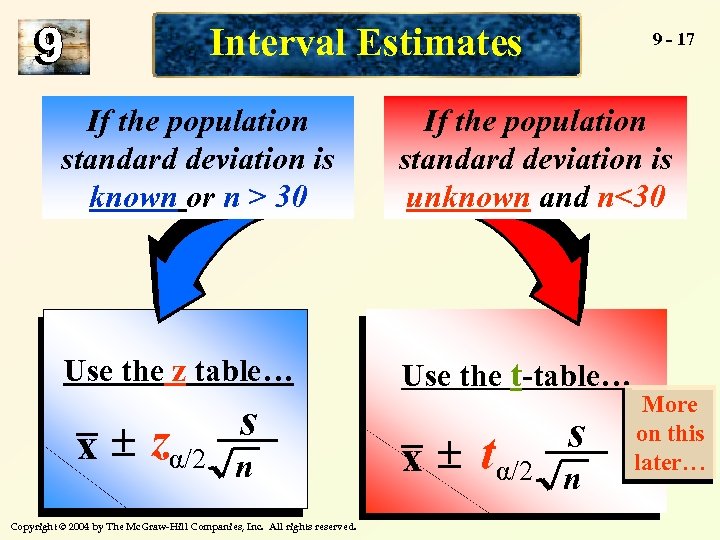Interval Estimates 9 - 17 If the population standard deviation is known or n > 30 If the population standard deviation is unknown and n<30 Use the z table… Use the t-table… n x Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. x ± zα/2 s ± t α/2 s n More on this later…

9 - 18 The Dean of the Business School wants to estimate the mean number of hours worked per week by students. A sample of 49 students showed a mean of 24 hours with a standard deviation of 4 hours. What is the population mean? Our best estimate is 24 hours. This is a point estimate. Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Find the 95 percent confidence interval for the population mean. 9 - 19 Commonly denoted as 1 - ± zα/2 s Mean = 24 SD = 4 N = 49 n Z = +/- 1. 96 x 95% Confidence Substitute values: 24 + 1. 96 4 49 = 24 +/- 1. 12 The Confidence Limits range from 22. 88 Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. to 25. 12

Interval Estimates 90% confidence level 1 - = 0. 9 or = 0. 10 99% confidence level 1 - = 0. 99 or = 0. 010 Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 20

Student’s t-distribution …. used for small sample 9 - 21 sizes Characteristics …like z, the t-distribution is continuous …takes values between – 4 and +4 …it is bell-shaped and symmetric about zero …it is more spread out and flatter at the centre than the z-distribution …for larger and larger values of degrees of freedom, the t-distribution becomes closer and closer to the standard normal distribution Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

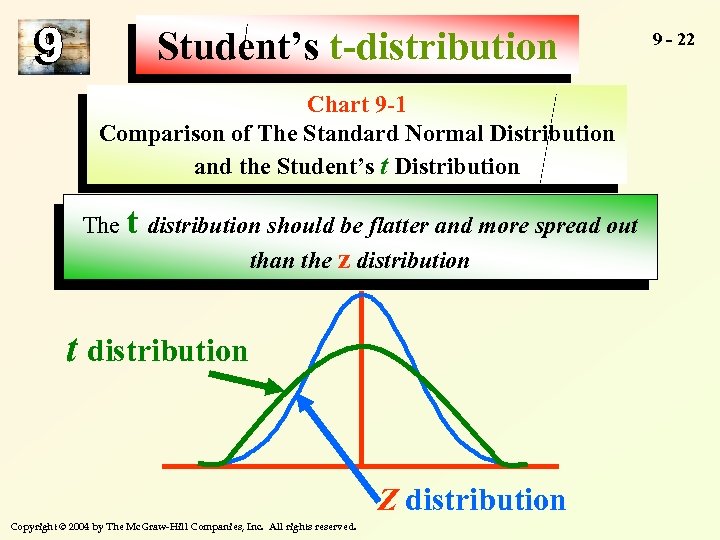Student’s t-distribution Chart 9 -1 Comparison of The Standard Normal Distribution and the Student’s t Distribution The t distribution should be flatter and more spread out than the z distribution t distribution Z distribution Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 22

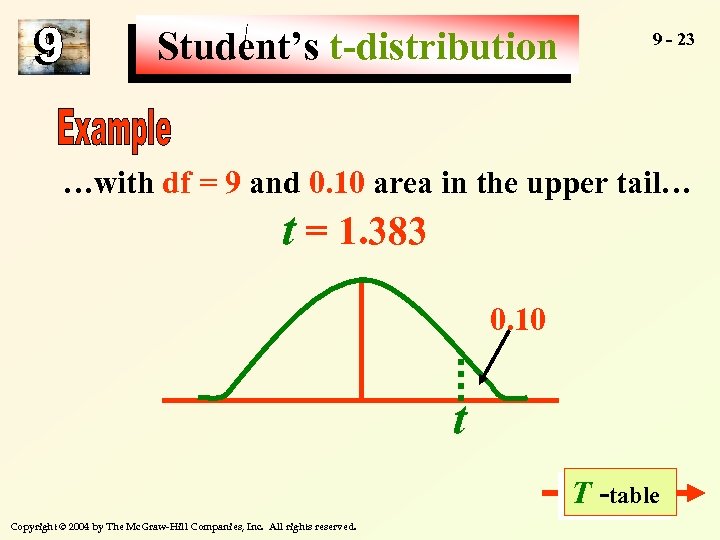Student’s t-distribution 9 - 23 …with df = 9 and 0. 10 area in the upper tail… t = 1. 383 0. 10 t T -table Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

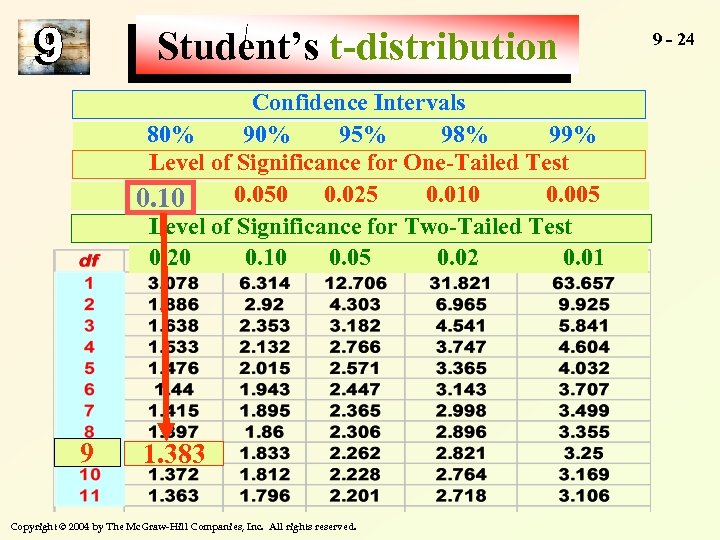Student’s t-distribution Confidence Intervals 80% 95% 98% 99% Level of Significance for One-Tailed Test 0. 100 0. 050 0. 025 0. 010 0. 005 0. 10 Level of Significance for Two-Tailed Test 0. 20 0. 10 0. 05 0. 02 0. 01 9 1. 383 Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 24

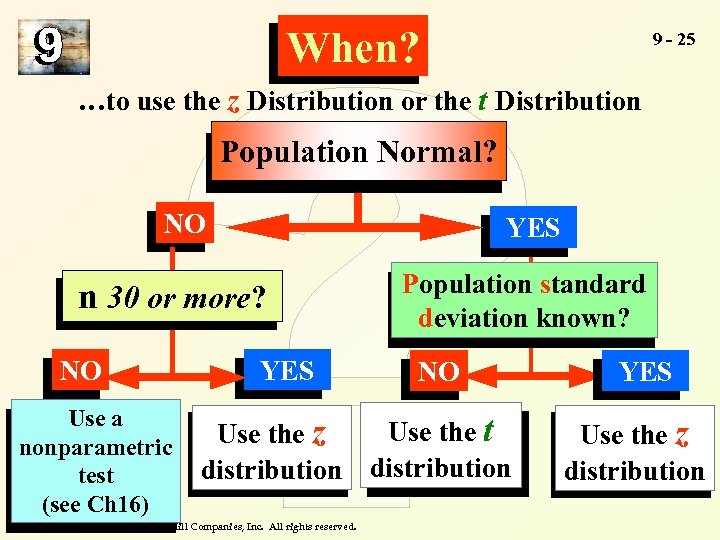When? 9 - 25 …to use the z Distribution or the t Distribution Population Normal? NO YES n 30 or more? NO Use a nonparametric test (see Ch 16) YES Population standard deviation known? NO Use the t Use the z distribution Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. YES Use the z distribution

Student’s t-distribution The Dean of the Business School wants to estimate the mean number of hours worked per week by students. A sample of only 12 students showed a mean of 24 hours with a standard deviation of 4 hours. Find the 95 percent confidence interval for the population mean. n is small so use the t - Distribution Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 26

…sample of only 12 students Data …a mean of 24 hours …a standard deviation of 4 hours = 24 n = 12 s=4 x Formula ± tα/2 df = 12 -1 = 11 X Looking up 5% level of significance for a two-tailed test with 11 df, we find… Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 27 s n = 1 – 95% =. 05

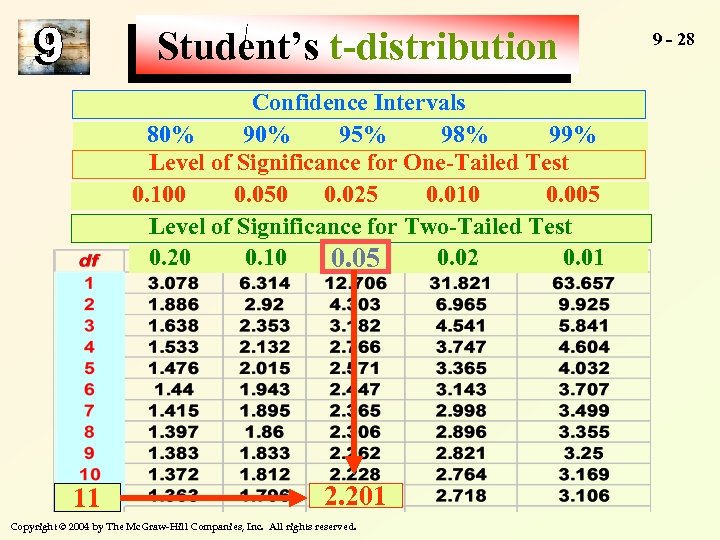Student’s t-distribution Confidence Intervals 80% 95% 98% 99% Level of Significance for One-Tailed Test 0. 100 0. 050 0. 025 0. 010 0. 005 Level of Significance for Two-Tailed Test 0. 20 0. 10 0. 05 0. 02 0. 01 0. 05 11 2. 201 Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 28

…sample of only 12 students Data …a mean of 24 hours …a standard deviation of 4 hours = 24 n = 12 s=4 x Formula ± tα/2 df = 12 -1 = 11 9 - 29 s n = 1 – 95% =. 05 X Looking up 5% level of significance for t 0. 025 = 2. 201 a two-tailed test with 11 df, we find… 4 24 ± 2. 201 12 = 24 +/- 2. 54 The confidence limits range from 21. 46 to 26. 54 Compare these with earlier limits of 22. 88 to 25. 12 Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Student’s t-distribution The manager of the college cafeteria wants to estimate the mean amount spent per customer purchase. A sample of 10 customers revealed the following amounts spent: $4. 45 $4. 05 $4. 95 $3. 25 $4. 68 $5. 75 $6. 01 $3. 99 $5. 25 $2. 95 Determine the 99% confidence interval for the mean amount spent. Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 30

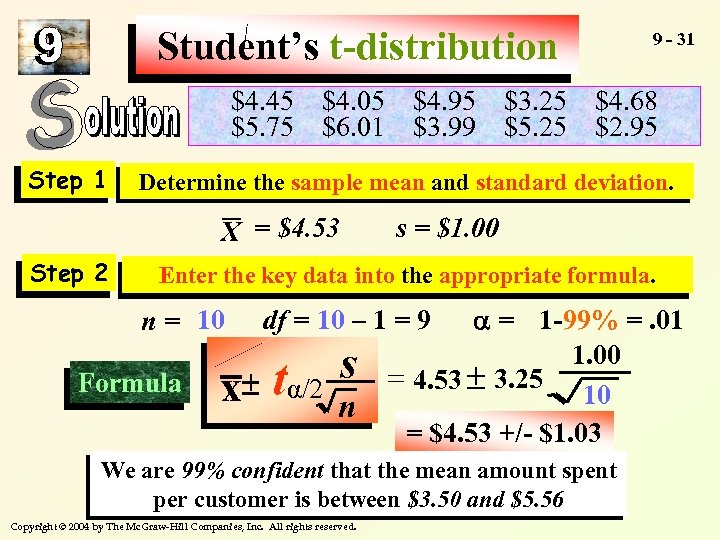Student’s t-distribution $4. 45 $5. 75 Step 1 $4. 95 $3. 99 $3. 25 $5. 25 $4. 68 $2. 95 Determine the sample mean and standard deviation. X Step 2 $4. 05 $6. 01 9 - 31 = $4. 53 s = $1. 00 Enter the key data into the appropriate formula. n = 10 x Formula = 1 -99% =. 01 1. 00 = 4. 53 ± 3. 25 10 = $4. 53 +/- $1. 03 df = 10 – 1 = 9 ± tα/2 s n We are 99% confident that the mean amount spent per customer is between $3. 50 and $5. 56 Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Constructing Confidence Intervals for Population Proportions A confidence interval for a population proportion is estimated by: Formula p …is the symbol for the sample proportion Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 32

Constructing Confidence Intervals for Population Proportions A sample of 500 executives who own their own home revealed 175 planned to sell their homes and retire to Victoria. Develop a 98% confidence interval for the proportion of executives that plan to sell and move to Victoria. Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 33

Constructing Confidence Intervals for Population Proportions A sample of 500 executives who own their own home revealed 175 planned to sell their homes and retire to Victoria. Develop a 98% confidence interval for the proportion of executives… 9 - 34 Formula n = 500 p = 175/500 =. 35 z = 2. 33 . 35 ± 2. 33 98% CL = Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. . 35 ( 1 -. 35 ) 500 . 35 ±. 0497

Finite-Population Correction Factor 9 - 35 Used when n/N is 0. 05 or more Formula sx = s n N - 1 Correction Factor The attendance at the college hockey game last night was 2700. A random sample of 250 of those in attendance revealed that the average number of drinks consumed person was 1. 8 with a standard deviation of 0. 40. Develop a 90% confidence interval estimate for the mean number of drinks consumed person. Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Finite-Population Correction Factor X Formula ± Zα/2 9 - 36 s N -n N - 1 n The attendance at the college hockey game last night was 2700. N = 2700 n = 250 x = 1. 8 A sample of 250 of s = 0. 40 /2 = 0. 05 those in attendance revealed that the average number of drinks consumed per Since 250/2700 >. 05, use the correction factor person was 1. 8 with a standard deviation of. 4 2700 - 250 0. 40. 1. 8 ± 1. 645 ( )( ) Develop a 90% 2700 -1 250 confidence interval estimate. … 90% CL = 1. 8 ± 0. 04 Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

9 - 37 Selecting the Sample Size Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Factors …that determine the sample size are: 1. The degree of confidence selected 2. The maximum allowable error 3. The variation in the population Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 38

Selecting the Sample Size Formula 9 - 39 æ zα/2 s ö 2 ÷ n =ç è E ø E … is the allowable error Z …is the z-score for the chosen level of confidence S …is the sample deviation of the pilot survey Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Selecting the Sample Size A consumer group would like to estimate the mean monthly electricity charge for a single family house in July (within $5) using a 99 percent level of confidence. Based on similar studies the standard deviation is estimated to be $20. 00. How large a sample is required? Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 40

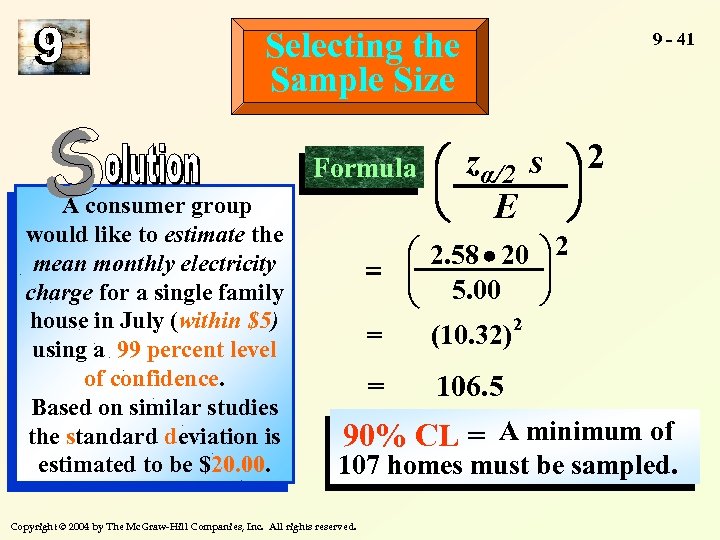Selecting the Sample Size Formula æ zα/2 s ö 2 ç ÷ è E ø æ 2. 58 · 20 2 = ç è 5. 00 = (10. 32)2 æ ç è A consumer group would like to estimate the mean monthly electricity charge for a single family house in July (within $5) using a 99 percent level of confidence. Based on similar studies the standard deviation is estimated to be $20. 00. 9 - 41 = 106. 5 90% CL = A minimum of 107 homes must be sampled. Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Selecting the Sample Size 9 - 42 The Kennel Club wants to estimate the proportion of children that have a dog as a pet. Assume a 95% level of confidence and that the club estimates that 30% of the children have a dog as a pet. If the club wants the estimate to be within 3% of the population proportion, how many children would they need to contact? Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Selecting the Sample Size New The Kennel Club wants to estimate the proportion of children that have a dog as a pet. Assume a 95% level of confidence and that the club estimates that 30% of the children have a dog as a pet. Formula 9 - 43 æZ ö 2 n = p (1 - p ) ç ÷ èE ø æ 1. 96 ö 2 =. 3 (1 -. 3 ) ç ÷ è. 03 ø = (. 21 )( 65. 33 ) 2 n = 896. 4 A minimum of 897 children must be sampled. Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Test your learning… on… lick C www. mcgrawhill. ca/college/lind Online Learning Centre for quizzes extra content data sets searchable glossary access to Statistics Canada’s E-Stat data …and much more! Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 44

9 - 45 This completes Chapter 9 Copyright © 2004 by The Mc. Graw-Hill Companies, Inc. All rights reserved.