8. Индексы

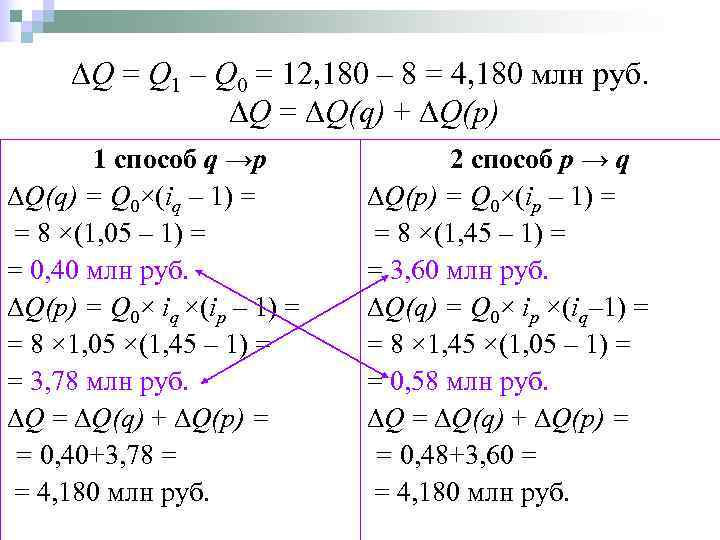
8. Индексы 8. 1. Общее понятие об индексах и их классификация 8. 2. Индивидуальные индексы 8. 3. Общие индексы 8. 4. Общие индексы как средние из индивидуальных 8. 5. Индексный анализ итогового показателя 8. 6. Индексы средних величин 8. 7. Цепные и базисные индексы 8. 8. Территориальные индексы

8. 1. Общее понятие об индексах и их классификация

Индекс (index - показатель, указатель, список) – это относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления в других условиях. Индексы используются для n характеристики выполнения плана, n для изучения динамики, n для сравнения уровней социально- экономических явлений по территориям, n для изучения роли факторов, оказывающих влияние на изменение данного явления.

Как правило сопоставляемые показатели характеризуют явления, состоящие из разнородных качественных элементов, суммирование которых невозможно из-за их несоизмеримости. Например, предприятие выпускает несколько видов продукции и оказывает различные услуг. Получить общий объём выпущенной продукции и оказанных услуг, применяя только натуральные единицы измерения невозможно. В этом случае следует использовать метод соизмерения. В качестве соизмерителя может выступать цена, себестоимость, трудоемкость единицы продукции и ряд других показателей.

Применение индексов дает нам возможность провести экономический анализ социально-экономических явлений в двух направлениях: 1. синтетическом и 2. аналитическом. Синтетическое направление определяет индекс как показатель среднего изменения уровня изучаемого явления. Аналитическое направление трактует индекс как показатель изменения уровня результативной величины под влиянием изменения индексируемой величины. Величина, изменение которой изучается в данном конкретном случае с помощью индекса, называется индексируемой величиной. Например, индекс физического объёма товарооборота фирмы (Iq) составил 115% или 1, 15. Полученный результат можно интерпретировать следующим образом: n на уровне синтетического анализа - физический объём товарооборота фирмы увеличился в отчетном периоде по сравнению с базисным на 15%; n на уровне аналитического анализа - в результате роста количества проданных товаров товарооборот фирмы увеличился в отчетном периоде по сравнению с базисным на 15%.

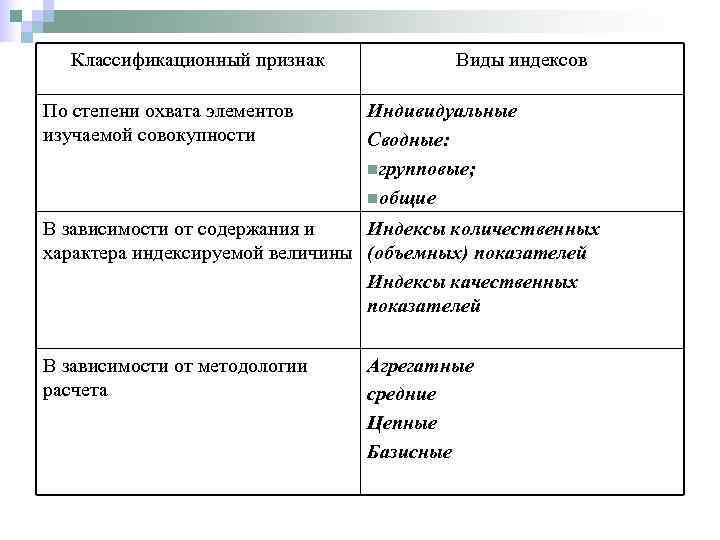
Способы построения индексов зависят от n содержания изучаемых явлений, n методологии расчета исходных статистических показателей и n целей исследования. В основу классификации индексов можно положить следующие признаки: n степень охвата элементов изучаемой совокупности, n содержание и характер индексируемой величины, n методология расчета.

Классификационный признак Виды индексов По степени охвата элементов Индивидуальные изучаемой совокупности Сводные: nгрупповые; nобщие В зависимости от содержания и Индексы количественных характера индексируемой величины (объемных) показателей Индексы качественных показателей В зависимости от методологии Агрегатные расчета средние Цепные Базисные

8. 2. Индивидуальные индексы

Индивидуальный индекс - это относительный показатель, выражающий изменение отдельного элемента сложного экономического явления.

Если выручка от продажи некоторого товара возросла с 8 млн руб. в предыдущем периоде до 12, 180 млн руб. в последующем и известо, что это объясняется увеличением количества проданного товара на 5% при цене на 45% большей, чем в предыдущем периоде, то можно записать следующее соотношение: 12, 180 = 8× 1, 05× 1, 45 млн руб.

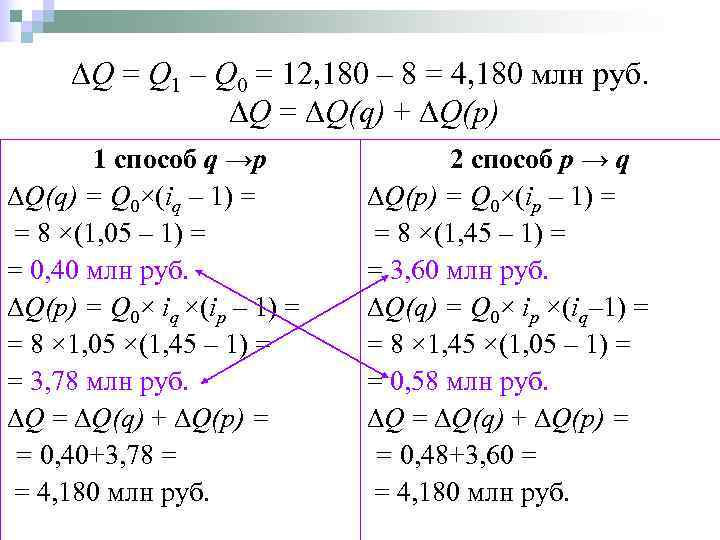Q = Q 1 – Q 0 = 12, 180 – 8 = 4, 180 млн руб. Q = Q(q) + Q(p) 1 способ q →p 2 способ p → q Q(q) = Q 0×(iq – 1) = Q(p) = Q 0×(ip – 1) = = 8 ×(1, 05 – 1) = = 8 ×(1, 45 – 1) = = 0, 40 млн руб. = 3, 60 млн руб. Q(p) = Q 0× iq ×(ip – 1) = Q(q) = Q 0× ip ×(iq– 1) = = 8 × 1, 05 ×(1, 45 – 1) = = 8 × 1, 45 ×(1, 05 – 1) = = 3, 78 млн руб. = 0, 58 млн руб. Q = Q(q) + Q(p) = = 0, 40+3, 78 = = 0, 48+3, 60 = = 4, 180 млн руб.

1 способ q →p 2 способ p → q Q(q) = Q 0×(iq – 1) = Q(p) = Q 0×(ip – 1) = = Q 0×iq – Q 0 = Q 0×ip – Q 0 Q(p) = Q 0× iq ×(ip – 1) = Q(q) = Q 0× ip ×(iq– 1) = = Q 0× iq ×ip – Q 0× iq = Q 0× iq ×ip – Q 0× ip Q = Q(q) + Q(p) = = Q 0× iq ×ip – Q 0 = =Q 0× iq ×ip – Q 0 = = Q 0 ( iq ×ip – 1)

Если товарооборот увеличился на 15%, цена уменьшилась на 5 %, то физический объем увеличился на 21%.

8. 3. Общие индексы

Сводный индекс выражает соотношение величин сложного экономического явления, состоящего из элементов непосредственно несоизмеримых. Сводные индексы могут быть: n групповые. Групповой индекс рассчитывается для группы элементов, входящих в общую совокупность. Например, индекс цен для товаров, входящих в какую- либо товарную группу (молоко и молочные продукты, аудио- и видеотехника и т. д. ). n общие. Общий индекс рассчитывается для всей совокупности элементов изучаемого явления. Общий индекс иногда употребляется как синоним понятия сводного индекса.

Основной формулой для расчета сводного индекса является агрегатная формула, в которой с помощью весов индекса несоизмеримые величины приводятся к соизмеримому виду.

1 способ q →p 2 способ p → q Индекс Пааше Индекс Лайспериса

Формулы расчета наиболее известных агрегатных индексов: 1. Индекс изменения общей суммы затрат на производство продукции в зависимости от объема производства(q) и затрат на единицу (z):

2. Индекс изменения общего фонда оплаты труда в связи с изменением общей численности работающих (Т) и заработной платы (f):

3. Индекс изменения объема продукции в связи с изменением численности работающих (Т) и уровня их выработки (w):

4. Индекс изменения объема продукции в связи с изменением объема основных производственных фондов (Ф) и показателя эффективности их использования (Н):

Примером мультипликативной индексной модели с большим числом факторов является изменение общей численности суммы материальных затрат на производство продукции. Сумма затрат (M) зависит от n количества выпущенной продукции (индекс Iq), n удельных расходов (норм) материала на единицу продукции (индекс In) и n цены на материалы (индекс Ip).

8. 4. Общие индексы как средние из индивидуальных

Средние индексы рассчитываются в тех случаях, когда нет необходимой информации для расчета агрегатного индекса.

Индекс общего объема товарооборота в форме средней арифметической:

Индекс общего объема товарооборота в форме средней геометрической:

Индекс физического объема в форме средней арифметической:

Доля i товарооборота в общем товарообороте

Индекс цен в форме средней геометрической:

При построении средних индексов следует руководствоваться следующим правилом: n для индекса количественного показателя используют формулу среднего арифметического индекса, n а для индекса качественного показателя - среднего гармонического индекса.

8. 5. Индексный анализ итогового показателя

Индекс числа работающих

Вклад разных факторов в общий прирост можно распределить по отдельным объектам, для каждого из которых применяют мультипликативную индексную модель: q 1=q 0·I T·id·iw

8. 6. Индексы средних величин

Из формулы средней следует, что на среднюю величину оказывает влияние как значение осредняемого признака, так и численность отдельных вариантов изучаемой совокупности.

Индекс переменного Индекс постоянного Индекс структурных состава (индекс (фиксированного) сдвигов средних величин) состава

8. 7. Цепные и базисные индексы

Для изучения динамики явления за ряд периодов возможно вычисление системы цепных и базисных индексов. Построение такой системы возможно в двух вариантах: 1. Оценивают относительное изменение уровня изучаемого явления по сравнению с каким-то одним определенным периодом времени. В этом случае строится система индексов с постоянной базой сравнения, то есть базисные индексы. 2. Оценивают относительное изменение уровня изучаемого явления по сравнению с предшествующим периодом. В этом случае строится система индексов с переменной базой сравнения, то есть цепные индексы.

I 4/0=I 1/0 I 2/1 I 3/2 I 4/3 I 4/3=I 4/0: I 3/0

8. 8. Территориальные индексы

Для выражения соотношения экономических явлений в пространстве ( по городам, регионам, странам и т. д. ) используют территориальные индексы. При построении территориальных индексов особое значение приобретает вопрос о весах индекса.

Территориальные индексы для качественных показателей Например, при сравнении уровня себестоимости по двум регионам в качестве веса может быть: n количество произведенной продукции каждого региона. Различия индексов, рассчитанных с весами разных регионов, могут быть существенными; n средний уровень для всей страны, региона и т. д. ; n стандартизованный (одинаковый) вес, общий для всех регионов. В этом случае территориальный индекс себестоимости будет равен: где z. А и z. Б - себестоимость произведенной продукции по видам в регионе “А” и в регионе “Б”, q - количество продукции данного вида, выработанное по всей стране или региону. Аналогично рассчитываются территориальные индексы для других качественных показателей.

Территориальные индексы для количественных показателей При построении территориальных индексов для количественных показателей способ стандартизованных весов удобнее использовать в виде среднего арифметического индекса, в котором рассчитанные предварительно территориальные индексы для каждой отрасли экономики, взвешиваются затем по структуре отраслей страны или региона. Расчет можно произвести по формуле: где ix - территориальный индекс для отрасли, полученный на основе соотношения продукции отрасли по регионам, - доля данной отрасли во всей продукции региона или страны.