8 Алгоритмы построения

8 Алгоритмы построения графиков а)график таблично заданной функции Yi=f(xi), i=1…N; б) график функции в полярных координатах; в) график изолиний скалярного поля.

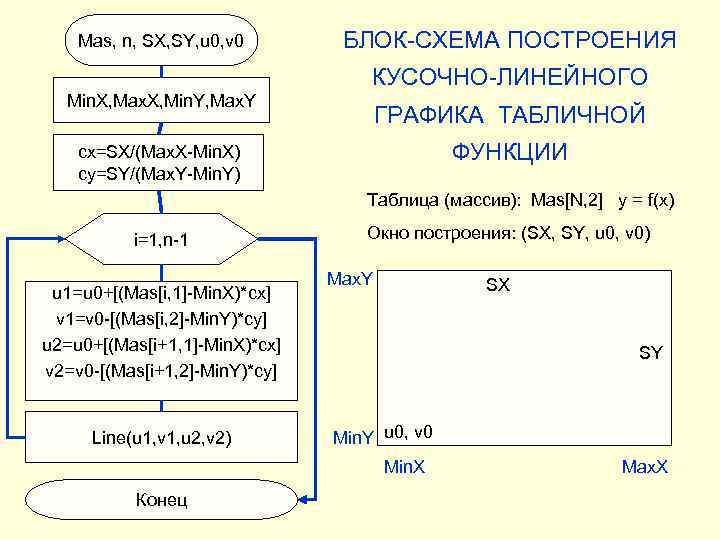
Mas, n, SX, SY, u 0, v 0 БЛОК-СХЕМА ПОСТРОЕНИЯ КУСОЧНО-ЛИНЕЙНОГО Min. X, Max. X, Min. Y, Max. Y ГРАФИКА ТАБЛИЧНОЙ cx=SX/(Max. X-Min. X) ФУНКЦИИ cy=SY/(Max. Y-Min. Y) Таблица (массив): Mas[N, 2] y = f(x) i=1, n-1 Окно построения: (SX, SY, u 0, v 0) Max. Y SX u 1=u 0+[(Mas[i, 1]-Min. X)*cx] v 1=v 0 -[(Mas[i, 2]-Min. Y)*cy] u 2=u 0+[(Mas[i+1, 1]-Min. X)*cx] SY v 2=v 0 -[(Mas[i+1, 2]-Min. Y)*cy] Line(u 1, v 1, u 2, v 2) Min. Y u 0, v 0 Min. X Max. X Конец

Процедура построения procedure Draw. Graph(Tag. Canvas: TCanvas; SX, SY, u 0, v 0: integer); var i, u 1, v 1, u 2, v 2: integer; cx, cy: real; begin cx: =SX/(Max. X-Min. X); cy: =SY/(Max. Y-Min. Y); with Tag. Canvas do begin Pen. Color: =cl. Blue; Pen. Width: =2; for i: =1 to n -1 do begin u 1: =u 0+round((Mas[i, 1]-Min. X)*cx); v 1: =v 0 - round((Mas[i, 2]-Min. Y)*cx); u 2: =u 0+round((Mas[i+1, 1]-Min. X)*cx); v 2: =v 0 - round((Mas[i+1, 2]-Min. Y)*cx); Move. To(u 1, v 1); Line. To(u 2, v 2); end; //with end;

Полярные координаты (ПК) Имеется единственная ось и некоторая точка на ней, называемая ПОЛЮСОМ. Любую точку на плоскости теперь можно определить парой чисел (R, ), где R – расстояние от полюса и - угол между осью и прямой, соединяющей полюс и данную точку (угол изменяется в направлении против часовой стрелки от оси).

Полярные координаты пчелы

Используют для обмена информацией об источниках пищи. Найдя новый источник пищи (клумбу, цветущее дерево, …), пчела-разведчица возвращается в улей, приносит образец и исполняет танец, на языке которого рассказывает, где находится пища. Танец состоит в том, что пчела, покачиваясь с боку на бок, прочерчивает прямую и затем, описав плавную кривую, возвращается в начальную точку. Участок прямой повторяется, но на этот раз она возвращается по кривой в другом направлении. Весь процесс повторяется несколько раз. Длина отрезка прямой даёт расстояние до пищи (в «пчелиных» единицах), а направление прямой – направление, в котором надо лететь. Таким образом пчела- разведчица сообщает другим пчёлам полярные координаты нового источника пищи.

АЛГОРИТМ ПОСТРОЕНИЯ Точка (R, ) в ПК – это то же самое что и точка (RCos( ), RSin( )) в декартовых координатах. Задаётся интервал изменения угла [ 1, 2] Задаётся шаг (приращение) угла В цикле для от 1 до 2 шагом вычисляются значения R = f( ). Определяются декартовые составляющие, которые собираются в массивы для последующего построения кусочно-линейного графика в заданном окне (SX, SY, u 0, v 0). При масштабировании изображения для сохранения угловых соотношений следует выбрать одинаковые коэффициенты перехода от физических величин к экранным (Если cx = SX/(Max_X-Min_X); cy = SY/(Max_Y – Min_Y), то выбирается Min(cx, cy) для обеих осей)

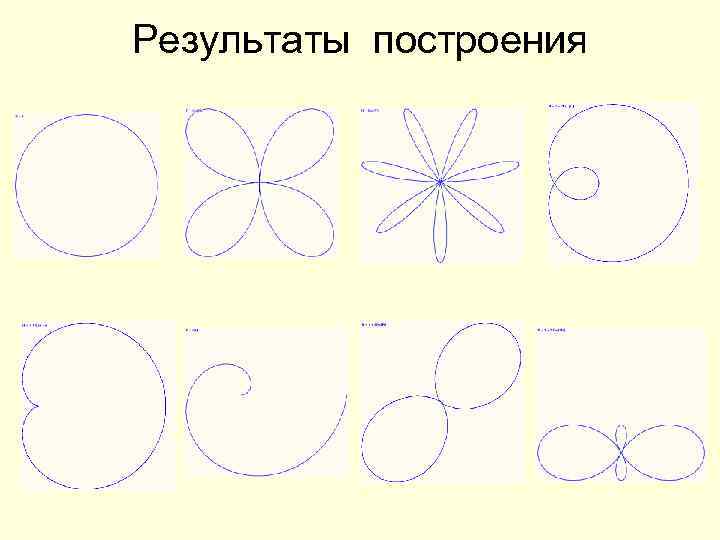
ФУНКЦИИ В ПОЛЯРНЫХ КООРДИНАТАХ R=1 Окружность R = Sin(2 ) Четырёхлепестковая роза R = Sin(7 ) Семилепестковая роза R = 1 + 2 Cos( ) Улитка Паскаля R = 1 + Cos( ) Кардиоида R = /4 Спираль R = 1 + Sin(2 ) Двухлепестковая роза R = 1 + 2 Cos(2 ) Петельное сцепление

Процедура заполнения массива procedure Fill. Mass(Variants: integer); var i: integer; Fi, r 1, r 2, R: real; begin Fi: =Fi 1; Count. Elems: =0; Min. X: =1 e 10; Max. X: = -1 e 10; Min. Y: =1 e 10; Max. Y: = -1 e 10; while Fi <=Fi 2 do begin Case Variants of 0: R: =1; 1: R: = Sin (2*Fi*Pi/180); 2: R : = Sin (7*Fi*Pi/180); 3: R: =1 + 2*Cos(Fi*Pi/180); 4: R: =1 + Cos(Fi*Pi/180); 5: R : = Fi*Pi/180 /4; 6: R : = 1 + Sin(2*Fi*Pi/180); 7: R : = 1 + 2*Cos(2*Fi*Pi/180); end; //case r 1: =R*Cos(Fi*Pi/180); r 2: =R*Sin(Fi*Pi/180); if r 1Max. X then Max. X: =r 1; if r 2Max. Y then Max. Y: =r 2; INC(Count. Elems); Mas[Count. Elems , 1]: =r 1; Mas[Count. Elems , 2]: =r 2; Fi: =Fi+d. Fi; end; //while end;

Результаты построения

ИЗОЛИНИИ ПОЛЯ

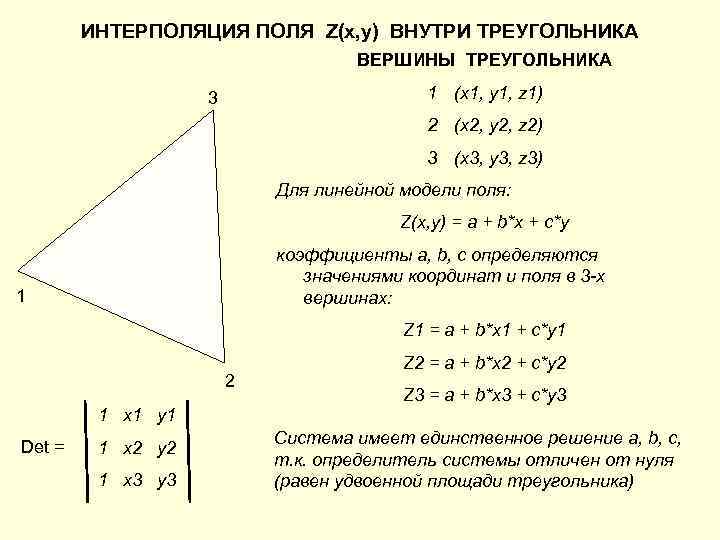
ИНТЕРПОЛЯЦИЯ ПОЛЯ Z(x, y) ВНУТРИ ТРЕУГОЛЬНИКА ВЕРШИНЫ ТРЕУГОЛЬНИКА 3 1 (x 1, y 1, z 1) 2 (x 2, y 2, z 2) 3 (x 3, y 3, z 3) Для линейной модели поля: Z(x, y) = a + b*x + c*y коэффициенты a, b, c определяются значениями координат и поля в 3 -х 1 вершинах: Z 1 = a + b*x 1 + c*y 1 Z 2 = a + b*x 2 + c*y 2 Z 3 = a + b*x 3 + c*y 3 1 x 1 y 1 Det = Система имеет единственное решение a, b, c, 1 x 2 y 2 т. к. определитель системы отличен от нуля 1 x 3 y 3 (равен удвоенной площади треугольника)

ВИЗУАЛИЗАЦИЯ ПОЛЯ Z(X, Y) ВНУТРИ ТРЕУГОЛЬНИКА 3 ПРОВЕДЕНИЕ ИЗОЛИНИЙ ПОЛЯ (изолиния – линия -> Z = const) АЛГОРИТМ Среди значений Z 1, Z 2, Z 3 выберем Max и Min (предполагается, что Min ≠Max, иначе задача теряет смысл) Зададим нужное число изолиний K_Izo 1 Определим шаг изолиний h = (Max-Min)/(K_Izo-1 ) Набор изолиний: 2 Z*(i) = Min +(i-1)*h; i = 1. . K_Izo при i=1: Z*(i) = Min; при i=K_Izo: Z*(i) = Min +(K_Izo-1)*h = Max. ХОД ИЗОЛИНИИ ВНУТРИ ТРЕУГОЛЬНИКА?

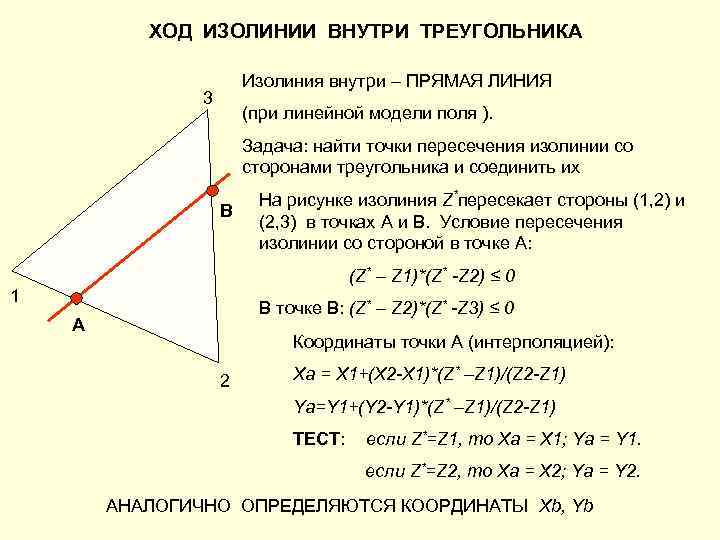
ХОД ИЗОЛИНИИ ВНУТРИ ТРЕУГОЛЬНИКА Изолиния внутри – ПРЯМАЯ ЛИНИЯ 3 (при линейной модели поля ). Задача: найти точки пересечения изолинии со сторонами треугольника и соединить их На рисунке изолиния Z*пересекает стороны (1, 2) и B (2, 3) в точках A и B. Условие пересечения изолинии со стороной в точке A: (Z* – Z 1)*(Z* -Z 2) ≤ 0 1 В точке B: (Z* – Z 2)*(Z* -Z 3) ≤ 0 A Координаты точки A (интерполяцией): 2 Xa = X 1+(X 2 -X 1)*(Z* –Z 1)/(Z 2 -Z 1) Ya=Y 1+(Y 2 -Y 1)*(Z* –Z 1)/(Z 2 -Z 1) ТЕСТ: если Z*=Z 1, то Xa = X 1; Ya = Y 1. если Z*=Z 2, то Xa = X 2; Ya = Y 2. АНАЛОГИЧНО ОПРЕДЕЛЯЮТСЯ КООРДИНАТЫ Xb, Yb

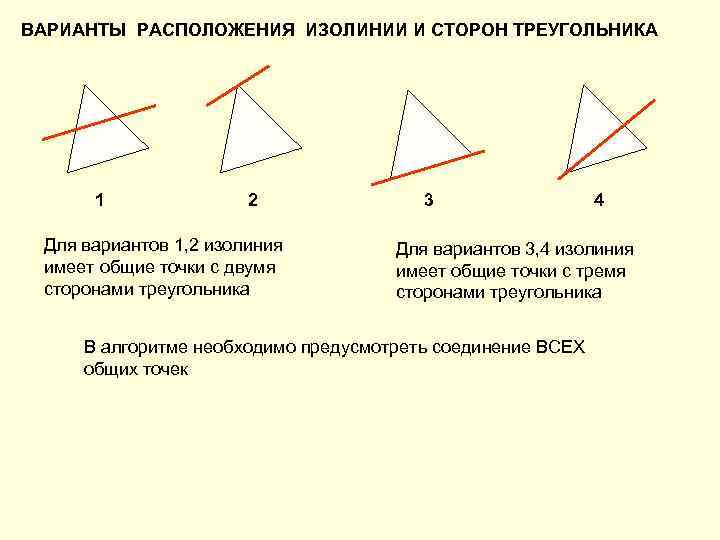
ВАРИАНТЫ РАСПОЛОЖЕНИЯ ИЗОЛИНИИ И СТОРОН ТРЕУГОЛЬНИКА 1 2 3 4 Для вариантов 1, 2 изолиния Для вариантов 3, 4 изолиния имеет общие точки с двумя имеет общие точки с тремя сторонами треугольника В алгоритме необходимо предусмотреть соединение ВСЕХ общих точек

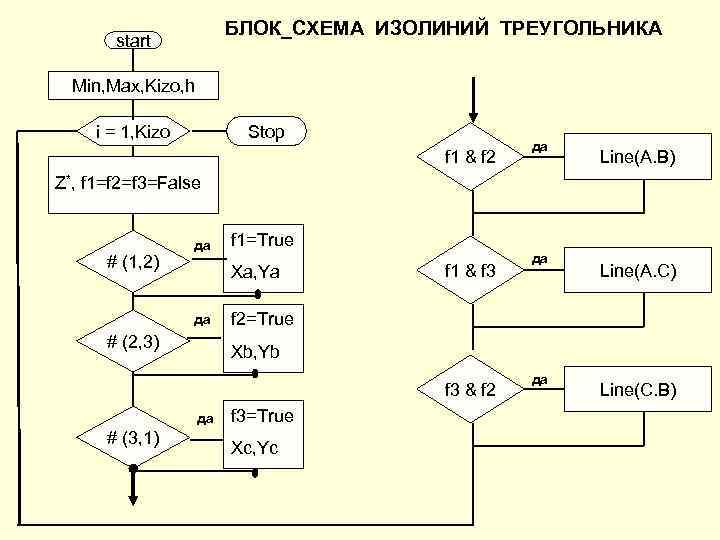
БЛОК_СХЕМА ИЗОЛИНИЙ ТРЕУГОЛЬНИКА start Min, Max, Kizo, h i = 1, Kizo Stop да f 1 & f 2 Line(A. B) Z*, f 1=f 2=f 3=False да f 1=True # (1, 2) да Xa, Ya f 1 & f 3 Line(A. C) да f 2=True # (2, 3) Xb, Yb да f 3 & f 2 Line(C. B) да f 3=True # (3, 1) Xc, Yc

ИЗОЛИНИИ ПОЛЯ Z(x, y), ЗАДАННОГО ТАБЛИЦЕЙ [m x n] n m Прямоугольник таблицы – область построения Координаты узлов (нормированы [0. . 1]): Xj – (горизонтальная) = (j-1)/(n-1); j=1. . n Yi- (вертикальная)= 1 -(i-1)/(m-1); i=1. . m Min, Max, K_Izo, h (Вертикальная координата имеет Z*(i) = Min +(i-1)*h; i = 1. . K_Izo направление обратное нумерации строк таблицы) ХОД ИЗОЛИНИИ ВНУТРИ ПРЯМОУГОЛЬНИКА?

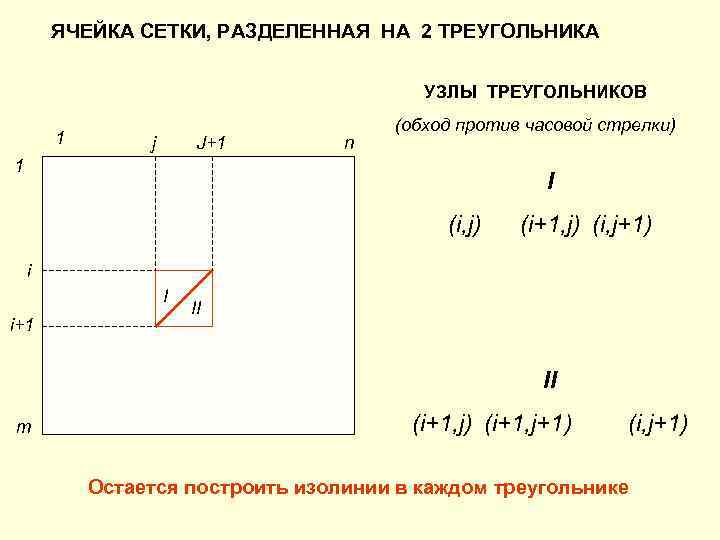
ЯЧЕЙКА СЕТКИ, РАЗДЕЛЕННАЯ НА 2 ТРЕУГОЛЬНИКА УЗЛЫ ТРЕУГОЛЬНИКОВ (обход против часовой стрелки) 1 j J+1 n 1 I (i, j) (i+1, j) (i, j+1) i II i+1 II m (i+1, j) (i+1, j+1) (i, j+1) Остается построить изолинии в каждом треугольнике

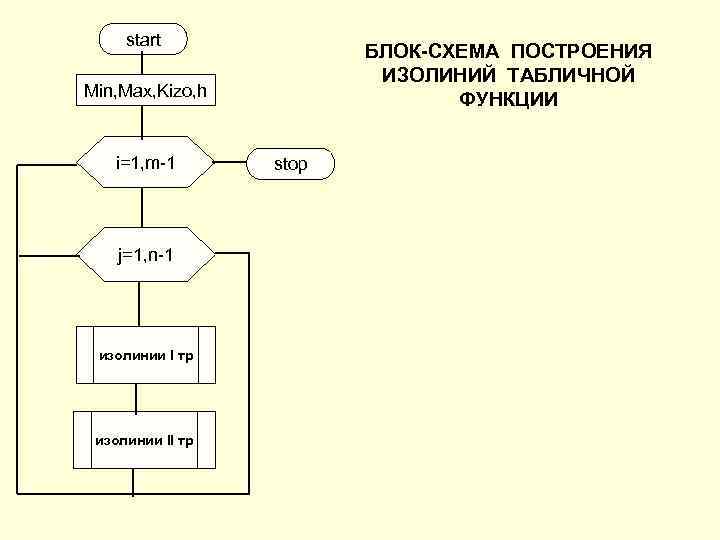
start БЛОК-СХЕМА ПОСТРОЕНИЯ ИЗОЛИНИЙ ТАБЛИЧНОЙ Min, Max, Kizo, h ФУНКЦИИ i=1, m-1 stop j=1, n-1 изолинии I тр изолинии II тр

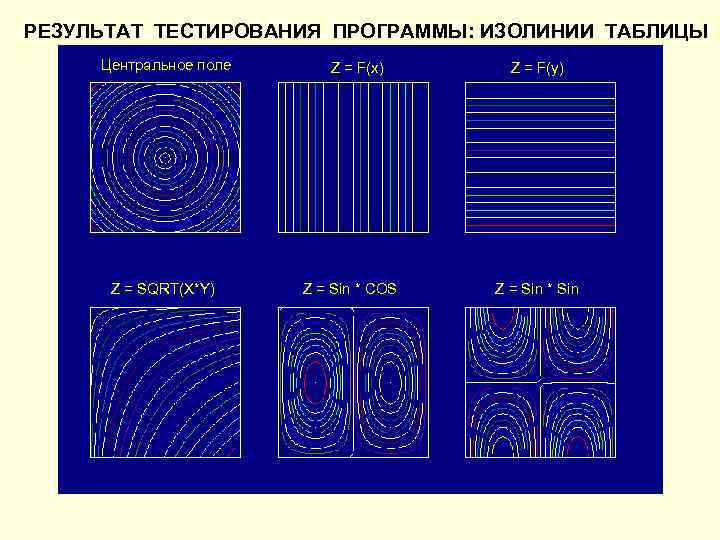
РЕЗУЛЬТАТ ТЕСТИРОВАНИЯ ПРОГРАММЫ: ИЗОЛИНИИ ТАБЛИЦЫ Центральное поле Z = F(x) Z = F(y) Z = SQRT(X*Y) Z = Sin * COS Z = Sin * Sin

The End