8 8 ЛЕКЦИЯ . . ПРОСТЕЙШИЕ ЭЛЕКТРОННЫЕ

8 8 ЛЕКЦИЯ. . ПРОСТЕЙШИЕ ЭЛЕКТРОННЫЕ ЦЕПИ И МЕТОДЫ ИХ АНАЛИЗА Электронная цепь (ЭЦ) – совокупность электронных компонентов, соединенных определенным образом, предназначенная для реализации заданной передаточной функции (ПФ) над входными сигналами. Анализ ЭЦ предполагает вывод ПФ и расчет ее параметров. Передаточной функцией К(р) будем называть отношение K ( p ) = Y ( p )/ X ( p ) изображений по Лапласу выходной величины Y ( p ) анализируемой цепи к входной X ( p ). Законы Ома и Кирхгофа, а также все классические методы расчета справедливы и действуют для цепей, представленных в операторной форме. Основные режимы работы цепей анализируются из одного уравнения для ПФ и следуют просто как разные формы решения этого уравнения. Легкость перехода к спектральному представлению и анализу цепей, основанная на том, что преобразование Фурье является частным случаем преобразования Лапласа.

2. Применение операторного метода к расчету электрических цепей 2. 1. Прямое преобразование Лапласа Этот метод заключается в том, что из области функций действительного переменного решение переносится в область функций комплексного переменного p = с + j , где операции принимают более простой вид, а именно: вместо исходных дифференциальных или интегро-дифференциальных уравнений получаются алгебраические уравнения ; затем полученный решением алгебраических уравнений результат переводится обратно в область функций действительного переменного. Этот переход осуществляется с помощью формул или таблиц. сходится абсолютно и является аналитической функцией комплексного переменного р = с + j . Интегральное уравнение вида (2. 1) представляет собой прямое преобразование Лапласа. Функция f ( t ) называется оригиналом , а функция F ( p ) — изображением по Лапласу. 0 dtetfp. F pt )()(Пусть f ( t ) — функция действительного переменного t , заданная в области t > 0 и равная нулю при t < 0. Известно, что если f ( t ) имеет ограниченный рост, то интеграл: (2. 1)

Следовательно, оригинал и изображение представляют собой пару функций действительного переменного t и комплексного переменного р , связанных преобразованием Лапласа. Из определения изображения следует, что каждый оригинал имеет единственное изображение. В свою очередь, оригинал вполне определяется своим изображением с точностью до значений в точках разрыва оригинала. Сокращенно переход от оригинала к изображению может быть записан в виде ff (( tt ) ) F F (( pp )) и, соответственно обратный переход FF (( pp ) ) f f (( tt ). ). Математическим операциям над оригиналами соответствуют определенные операции над изображениями и наоборот. Знание этих операций, или, как их называют, свойств преобразования Лапласа , облегчает нахождение изображений. Оно позволяет переходить от дифференциальных (или интегро-дифференциальных) уравнений, записанных для функций-оригиналов , к » операторным » уравнениям, записываемым для изображений , и облегчает последующее нахождение искомого оригинала по вычисленному изображению. Основные свойства преобразования Лапласа доказываются в курсе математического анализа. Ниже приводятся лишь формулировки этих свойств.

Теорема дифференцирования дифференцированию оригинала соответствует операция умножения изображения на р df ( t )/ dt p. F ( p ) — f (0_). Теорема интегрирования интегрированию оригинала соответствует операция деления на p f ( t ) dt F ( p )/ p. Теорема запаздывания запаздыванию во временной области соответствует умножение изображения на экспоненциальную функцию p f ( t — ) e — p F ( p ). Теорема смещения показывает, как изменяется изображение при умножении оригинала на экспоненциальную функцию времени e t f ( t ) F ( p — ). Теорема умножения изображений (теорема свертывания) устанавливает, что умножению изображений соответствует операция свертки оригиналов с пределами интегрирования от 0 до t F 1( p ) F 2( p ) f 1( t ) f 2( t — ) d. Теорема подобия показывает, как изменяется изображение при изменении масштаба независимой переменной t оригинала f ( at ) (1/ a ) F ( p / a ).

Теорема линейности устанавливает, что изображение линейной комбинации есть линейная комбинация изображений или, в самом простом случае, что умножение оригинала на постоянный коэффициент соответствует умножению изображения на этот же коэффициент af ( t ) a. F ( p ). Предельные соотношения. Первое предельное соотношение дает возможность найти начальное значение функции f ( t ) при t = 0 непосредственно по изображению: lim f ( t ) = lim p. F ( p ), при p . Второе предельное соотношение дает возможность найти предел функции f ( t ) при t по значению функции F ( p ) в начале координат: lim f ( t ) = lim p. F ( p ), при p 0. Предельные соотношения полезны для проверки вычислений с помощью преобразования Лапласа. 2. 2. 2. Обратное преобразование Лапласа позволяет перейти от изображений к оригиналам. Из теории функции комплексного переменного известно, что если функция F ( p ) аналитична и интегрируема в пределах от c — j до c + j , то существует интеграл jc jc pt dpep. F j tf)( 2 1 )( (2. 1)

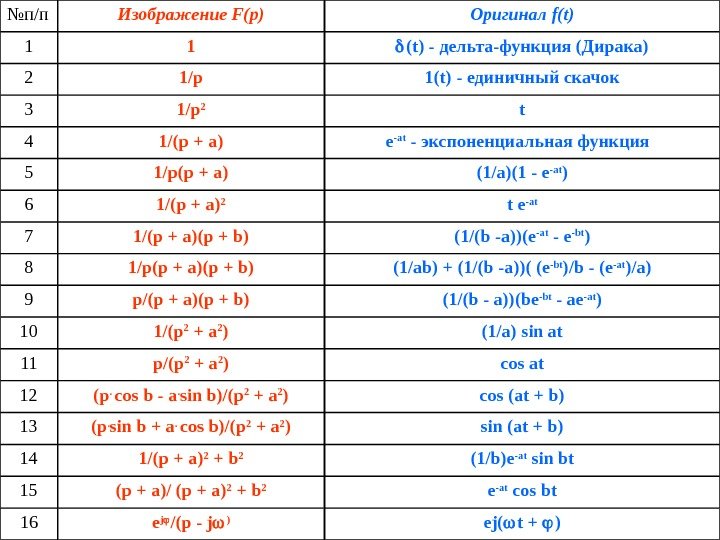
Эта формула, носящая название обратного преобразования Лапласа , представляет собой решение интегрального уравнения (2. 1) относительно функции f ( t ). Переход F ( p ) f ( t ) непосредственно по формуле (2. 2) не всегда удобен из-за сложности, поэтому на практике используют различные приближенные методы оценки вида функции f ( t ). При анализе сложных электрических цепей чаще всего применяют теорему о вычетах (теорему разложения), которая позволяет представить подинтегральное выражение в (2. 2) в виде суммы ряда простых слагаемых и заменить операцию интегрирования операцией суммирования этих слагаемых. Другой путь реализации обратного преобразования Лапласа заключается в использовании специальных таблиц, связывающих оригиналы и изображения. Эти таблицы составлены для множества функций F ( p ) и f ( t ) и приводятся в справочной математической литературе, в учебниках по теоретическим основам электротехники, теории сигналов и цепей. В табл. 2. 1 приведена выписка некоторых преобразований.

№ п/п Изображение F(p) Оригинал f(t) 1 1 (t) — дельта-функция (Дирака) 2 1 /p 1(t) — единичный скачок 3 1/p 2 t 4 1/(p + a) e -at — экспоненциальная функция 5 1 /p(p + a) (1/a)(1 — e -at ) 6 1/(p + a) 2 t e -at 7 1/(p + a)(p + b) (1/(b -a))(e -at — e -bt ) 8 1/p(p + a)(p + b) (1/ab) + (1/(b -a))( (e -bt )/b — (e -at )/a) 9 p/(p + a)(p + b) (1/(b — a))(be -bt — ae -at ) 10 1/(p 2 + a 2 ) (1/a) sin at 11 p/(p 2 + a 2 ) cos at 12 (p. cos b — a. sin b)/(p 2 + a 2 ) cos (at + b) 13 (p. sin b + a. cos b)/(p 2 + a 2 ) sin (at + b) 14 1/(p + a) 2 + b 2 (1/b)e -at sin bt 15 (p + a)/ (p + a) 2 + b 2 e -at cos bt 16 e j /(p — j ) ej( t + )

Анализ электронных цепей Анализ ЭЦ предполагает вывод ПФ и расчет ее параметров. Методика составления уравнения для ПФ содержит несколько этапов. Исходно должна быть задана топология анализируемой цепи и определено, что является входной величиной, а что — выходной. Порядок действий: 1) преобразование цепи в операторную форму; 2) составление системы алгебраических уравнений цепи по законам Ома и Кирхгофа в соответствии с выбранным методом расчета; 3) решение полученной системы относительно выходной величины; 4) запись решения в форме уравнения преобразования, когда неизвестная выходная величина Y ( p ) записывается в левой, а заданная входная величина X ( p ) — в правой части уравнения вместе с совокупностью компонент определяющих операторный коэффициент передачи: Y ( p ) = K ( p ) X ( p ); 5) запись уравнения для ПФ в виде K ( p ) = Y ( p )/ X ( p ); 6) качественный анализ ПФ как функции от оператора р с использованием предельных соотношений p 0 и p ; 7) переход от изображений к оригиналам либо в комплексной форме K ( j ), либо в показательной K ( t ); 8) численная оценка коэффициента передачи K ( ) на заданной частоте или K ( t ) в заданный момент времени и построение соответствующих зависимостей K ( ) или K ( t ).

3. 1 Основные характеристики электронных цепей Чтобы устранить неопределенности и унифицировать описания различных по топологии и назначению электрических цепей, электронных устройств, приборов и систем, специалисты договорились в качестве основных использовать следующие характеристики: 1) амплитудную (АХ); 2) амплитудно-фазочастотную (АФЧХ); 3) переходную (ПХ). Для каждой характеристики определен перечень основных параметров, с помощью которых производится сравнительная оценка качества различных устройств по диапазону преобразуемых величин, быстродействию, точности и др. Ряд этих параметров законодательно оговорен и используется как перечень обязательных паспортных параметров электронных устройств. Амплитудная характеристика (АХ) представляет собой зависимость амплитудного (или действующего) значения выходной величины цепи от амплитудного (или действующего) значения входной величины. В информационно-измерительной технике понятию АХ соответствует понятие уравнения преобразования (УП). Если АХ является линейной , то и такая электрическая цепь называется линейной.

АЧХ представляет собой реакцию цепи на входное воздействие в форме синусоидального сигнала. Для цепей с линейной АХ реакция цепи на входное воздействие в форме синусоидального сигнала будет иметь синусоидальную форму. Формально АЧХ можно определить как зависимость коэффициента передачи цепи от частоты входного сигнала K ( ). В свою очередь K ( ) равен модулю ПФ при замене p = j , т. е. K ( ) = Re 2 [ K ( p = j )] + Im 2 [ K ( p = j )], (2. 3) где символами Re 2 [ K ( p = j )] и Im 2 [ K ( p = j )] обозначены соответственно квадраты действительной и мнимой частей комплексной ПФ K ( j ). Амплитудно-фазочастотная характеристика (АФЧХ) состоит из двух характеристик: амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ).

Поскольку коэффициент передачи, являясь параметром АХ, определяет ее наклон K = Y / X , где X , Y — входная и выходная величина цепи, а АЧХ K ( ) есть просто модуль передаточной функции, то становится понятной связь между АХ, АЧХ и ПФ. АХ — частный случай АЧХ для фиксированной час-ты ; АЧХ представляет частный случай ПФ для фиксированной синусоидальной формы входного воздействия. Чтобы проанализировать вид АЧХ и оценить ее параметры необходимо: 1) вывести выражение для ПФ заданной цепи; 2) заменить оператор р на j , 3) привести полученную комплексную ПФ к стандартному виду : K ( j ) = Re [ K ( j )] + j Im [ K ( j )], т. е. выделить отдельно действительную и мнимую части; 4) записать уравнение для АЧХ в форме (2. 3), т. е. найти модуль ПФ; 5) исследовать функцию K ( ) на предмет наличия характерных точек (экстремумов, разрывов, перегибов, асимптот, предельных значений и т. д. ).

ФЧХФЧХ находится как arctg отношения мнимой части комплексной ПФ к действительной части. Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) или диаграмма Боде, представляет собой АЧХ , построенную в логарифмическом масштабе и аппроксимированную отрезками прямых линий. Чтобы построить ЛАЧХ, необходимо уравнение для АЧХ прологарифмировать (в десятичных логарифмах) с коэффициентом 20 (для получения единиц измерения децибел ), а затем точные выражения, стоящие под знаком логарифма, заменить более простыми, приближенными. Переходная характеристика представляет собой реакцию цепи на входное воздействие в виде единичного скачка. ПХ так же, как и АЧХ, является частным случаем ПФ. В отличие от АЧХ, ПХ есть решение уравнения для ПФ в экспоненциальной (показательной) форме , для чего используются либо непосредственно формула обратного преобразования Лапласа , либо теорема о вычетах , либо таблицы. На практике из-за простоты чаще всего используют последний вариант. При небольшом навыке, запомнив два-три вида преобразования, можно научиться достаточно быстро решать типовые задачи.

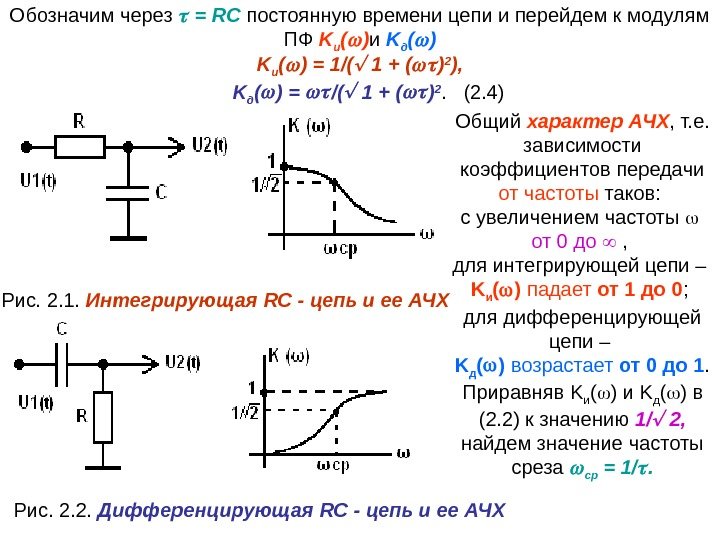
3. 2 Пример расчета электронных цепей Рассмотрим конкретную реализацию данной методики на примере двух простых, но очень важных как для теории, так и практики RC — цепей: интегрирующей (рис. 2. 1) и дифференцирующей (рис. 2. 2). Входной величиной в обоих случаях является напряжение U 1 ( t ), а выходной — напряжение U 2 ( t ). 1) Для перехода к операторной форме цепи заменим оригиналы напряжений и токов на их изображения U(t) U(p), U R (t) U R (p), U C (t) U C (p), I(t) I(p). Заменим элементы R , C их операторными сопротивлениями по правилу: R R, X С = 1/j C 1/p. C. 2) Второй закон Кирхгофа в операторной форме U(p) = U R (p) + U C (p) = I(p) Z(p) = I(p) ( R + 1/p. C ). 3) Так как входная величина U 1 ( p ), а выходная U 2 ( p ), сами цепи представляют собой делитель напряжения, для которого несложно вывести уравнение преобразования: U 2 ( p ) = U 1 ( p ) Z 2 ( p )/( Z 1 ( p ) + Z 2 ( p )). 4) Учитывая, что для интегрирующей (рис. 2. 1) цепи Z 1 ( p ) = R , Z 2 ( p ) = 1/ p. C , а для дифференцирующей (рис. 2. 2) — наоборот Z 1 ( p ) =1/ p. C , Z 2 ( p ) = R , получаем ПФ K и (p) = 1/(1 + p. RC); K д ( p ) = p. RC /(1 + p. RC ).

Рис. 2. 1. Интегрирующая RC — цепь и ее АЧХ Общий характер АЧХ , т. е. зависимости коэффициентов передачи от частоты таков: с увеличением частоты от 0 до , для интегрирующей цепи – K и ( ) падает от 1 до 0 ; для дифференцирующей цепи – K д ( ) возрастает от 0 до 1. Приравняв K и ( ) и K д ( ) в (2. 2) к значению 1/ 2, найдем значение частоты среза ср = 1/. Рис. 2. 2. Дифференцирующая RC — цепь и ее АЧХK и ( ) = 1/( 1 + ( ) 2 ), K д ( ) = /( 1 + ( ) 2. (2. 4) Обозначим через = RC постоянную времени цепи и перейдем к модулям ПФ K и ( ) и K д ( )

ЛАЧХ интегрирующей цепи K и [д. Б]=20 Lg ( K и ( ))= -10 Lg (1+( ) 2 ). Если текущее значение частоты меньше частоты среза ср , можно пренебречь 1 под знаком Lg , и тогда K и [д. Б] — 20 Lg ( ). Следовательно, ЛАЧХ интегрирующей цепи состоит из двух прямых, одна из которых совпадает с осью абсцисс ( K и [д. Б] 0 или, что то же самое, K и ( ) 1) в диапазоне от 0 до ср. Другая прямая наклонена к оси абсцисс с угловым коэффициентом -20 децибел на декаду (-20 д. Б/дек). Последнее означает, что на участке > ср , изменению частоты в 10 раз (т. е. на декаду) соответствует уменьшение коэффициента передачи тоже в 10 раз (или в логарифмических единицах на 20 д. Б). В относительной форме данная зависимость имеет вид K ( ) ( ср / ) или K ( f ) ( f ср / f ). Рис. 2. 3. ЛАЧХ интегрирующей (а)и дифференцирующей (б) цепей

ЛАЧХ дифференцирующей цепи K д [д. Б]=20 Lg ( K д ( ))=20 Lg ( ) — 10 Lg (1+( ) 2 ). Эта ЛАЧХ также состоит из двух прямых. Первая прямая K д [д. Б] 20 Lg ( ) соответствует диапазону изменения частоты от 0 до ср. В этом диапазоне наблюдается увеличение коэффициента передачи со скоростью 20 децибел на декаду. В относительной форме данная зависимость имеет вид K ( ) ( / ср ) или K ( f ) ( f / f ср ). Вторая прямая K д [д. Б] 0 д. Б , совпадающая с осью абсцисс, лежит в диапазоне изменения частоты от ср до . ЛАЧХ интегрирующей и дифференцирующей цепей представлены на рис. 2. 3. Обратите внимание на то, что при построении ЛАЧХ координаты точек по оси абсцисс могут указываться не в логарифмических единицах , а непосредственно в Гц или рад/с , а по оси ординат — в единицах измерения коэффициента передачи (как правило, в относительных единицах).

Анализ переходной характеристики интегрирующей и дифференцирующей цепей, ПФ которых: KK ии (p) = 1/(1 + p. RC); KK дд (p) = p. RC/(1 + p. RC). Учитывая, что изображение функции, которая называется единичным скачком 1( tt ) есть 1/ pp (табл. 2. 1), преобразуем общие ПФ KK ии (( pp ) и KK дд (( pp ) к частному виду WW ии (( pp ) и WW дд (( pp ), используя замену UU 11 (( pp ) = EE // pp. Здесь EE — — некоторое произвольное значение скачка входного напряжения. WW ии (( pp ) = UU 22 (( pp )/)/ EE = = KK ии (( pp )/)/ pp = 1/ pp (1 + p. RC ); ); WW дд (( pp ) = UU 22 (( pp )/)/ EE = = KK дд (( pp )/)/ pp = = RCRC /(1 + p. RC ). ). (2. 5) Произведем замену = = RCRC и вынесем эту постоянную времени в знаменателях (2. 2) за скобки. В результате получим формулы, соответствующие формулам п. 5 и п. 4 табл. 2. 1, где aa = 1/ : : WW ии (( pp ) = aa // pp (( pp + + aa ); ); WW дд (( pp )) = 1/( pp + + aa ). ). (2. 6) Переходя по таблице 2. 1 от изображений к оригиналам , получаем ПХ для интегрирующей и дифференцирующей цепей (рис. 2. 6) в виде WW ии (t) = U 22 (t)/E = (1 — exp( — t/ )); WW дд (t) = U 22 (t)/E = exp( — t/ ). ). (2. 7)

Основными параметрами ПХ являются постоянная времени и время установления t у. Временем установления называется интервал времени между моментом подачи входного единичного скачка и моментом достижения функцией W и ( t ) значения, равного 0, 9 от max ( W и ( t )) или моментом достижения функцией W д ( t ) значения, равного 0, 1 от max ( W д ( t )). Подставив в (2. 7) вместо W и ( t ) 0, 9 , а вместо W д ( t ) 0, 1 , получим t у = . Ln 10 2, 3 . . Примерно через такое время переходный процесс в цепи заканчивается. Постоянная времени , , как параметр ПХ, связана с частотой среза — параметром АЧХ, соотношением срср = 1/. . Рис. 2. 4. Переходные характеристики RC –цепей. Связь ПХ и АЧХ позволяет, например, зная реакцию цепи на единичный скачок , предсказывать поведение цепи при синусоидальном входном сигнале , не проводя дополнительных экспериментов.