8 8 Exponential Growth Decay

8. 8 – Exponential Growth & Decay

Decay:

Decay: 1. Fixed rate

Decay: 1. Fixed rate: y = a(1 – r)t

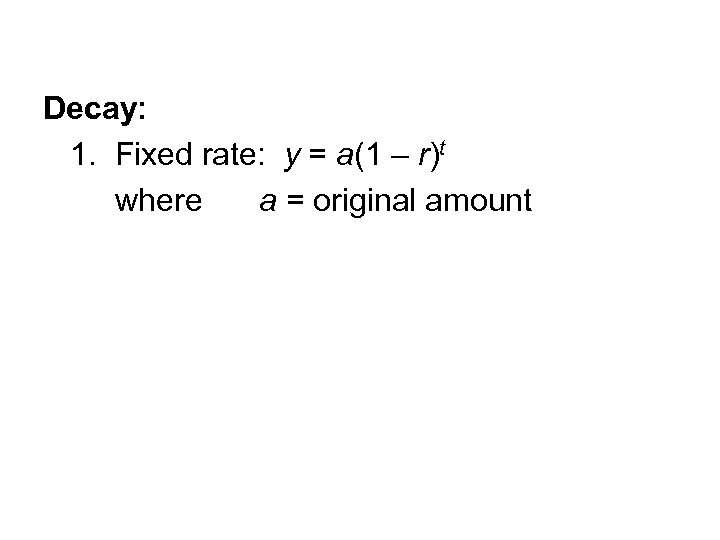Decay: 1. Fixed rate: y = a(1 – r)t where a = original amount

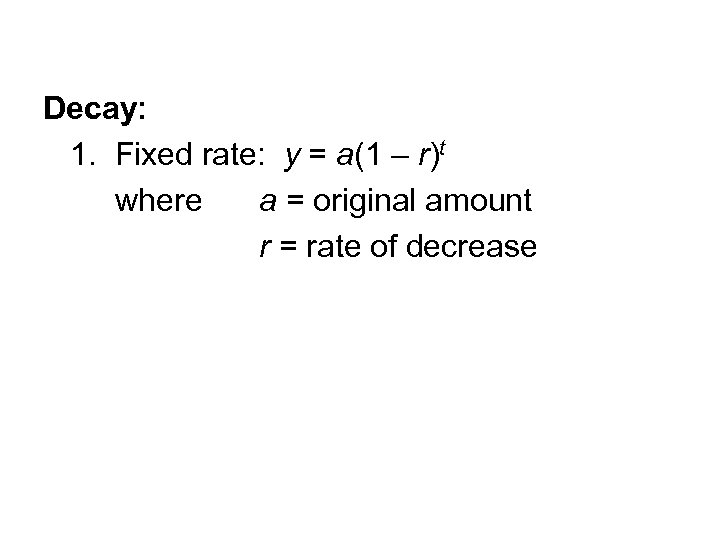Decay: 1. Fixed rate: y = a(1 – r)t where a = original amount r = rate of decrease

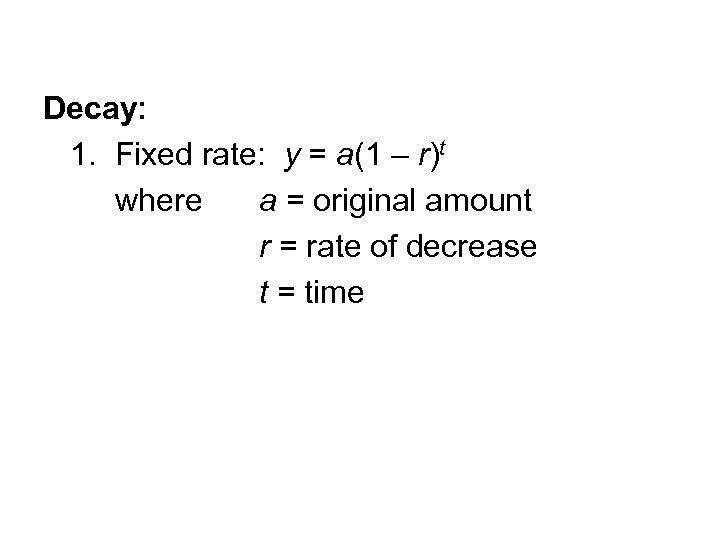Decay: 1. Fixed rate: y = a(1 – r)t where a = original amount r = rate of decrease t = time

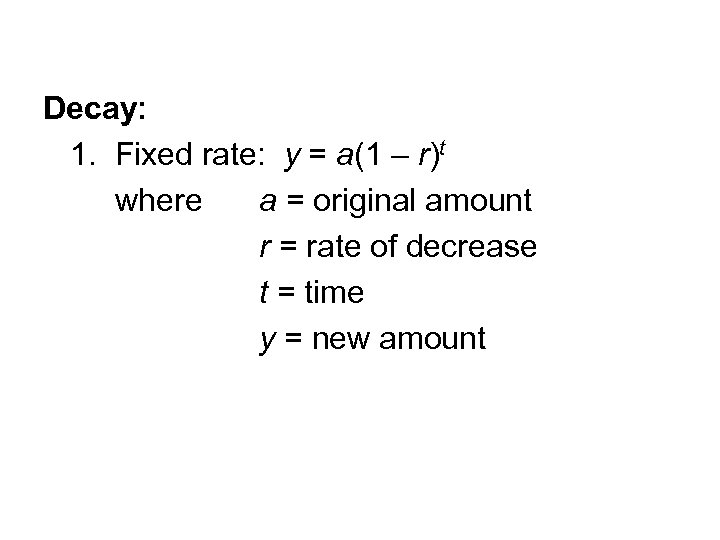Decay: 1. Fixed rate: y = a(1 – r)t where a = original amount r = rate of decrease t = time y = new amount

Decay: 1. Fixed rate: y = a(1 – r)t where a = original amount r = rate of decrease t = time y = new amount Ex. 1 A cup of coffee contains 130 mg. of caffeine. If caffeine is eliminated from the body at a rate of 11% per hour, how long will it take for half of this caffeine to be eliminated from a person’s body?

Decay: 1. Fixed rate: y = a(1 – r)t where a = original amount r = rate of decrease t = time y = new amount Ex. 1 A cup of coffee contains 130 mg. of caffeine. If caffeine is eliminated from the body at a rate of 11% per hour, how long will it take for half of this caffeine to be eliminated from a person’s body? 11% indicates that it is fixed-rate decay.

Decay: 1. Fixed rate: y = a(1 – r)t where a = original amount r = rate of decrease t = time y = new amount Ex. 1 A cup of coffee contains 130 mg. of caffeine. If caffeine is eliminated from the body at a rate of 11% per hour, how long will it take for half of this caffeine to be eliminated from a person’s body? 11% indicates that it is fixed-rate decay. y = a(1 – r)t

Decay: 1. Fixed rate: y = a(1 – r)t where a = original amount r = rate of decrease t = time y = new amount Ex. 1 A cup of coffee contains 130 mg. of caffeine. If caffeine is eliminated from the body at a rate of 11% per hour, how long will it take for half of this caffeine to be eliminated from a person’s body? 11% indicates that it is fixed-rate decay. y = a(1 – r)t a = 130

Decay: 1. Fixed rate: y = a(1 – r)t where a = original amount r = rate of decrease t = time y = new amount Ex. 1 A cup of coffee contains 130 mg. of caffeine. If caffeine is eliminated from the body at a rate of 11% per hour, how long will it take for half of this caffeine to be eliminated from a person’s body? 11% indicates that it is fixed-rate decay. y = a(1 – r)t a = 130 r = 0. 11

Decay: 1. Fixed rate: y = a(1 – r)t where a = original amount r = rate of decrease t = time y = new amount Ex. 1 A cup of coffee contains 130 mg. of caffeine. If caffeine is eliminated from the body at a rate of 11% per hour, how long will it take for half of this caffeine to be eliminated from a person’s body? 11% indicates that it is fixed-rate decay. y = a(1 – r)t a = 130 r = 0. 11 y=

Decay: 1. Fixed rate: y = a(1 – r)t where a = original amount r = rate of decrease t = time y = new amount Ex. 1 A cup of coffee contains 130 mg. of caffeine. If caffeine is eliminated from the body at a rate of 11% per hour, how long will it take for half of this caffeine to be eliminated from a person’s body? 11% indicates that it is fixed-rate decay. y = a(1 – r)t a = 130 r = 0. 11 y = 65

Decay: 1. Fixed rate: y = a(1 – r)t where a = original amount r = rate of decrease t = time y = new amount Ex. 1 A cup of coffee contains 130 mg. of caffeine. If caffeine is eliminated from the body at a rate of 11% per hour, how long will it take for half of this caffeine to be eliminated from a person’s body? 11% indicates that it is fixed-rate decay. y = a(1 – r)t a = 130 r = 0. 11 y = 65 t = ? ? ?

Decay: 1. Fixed rate: y = a(1 – r)t where a = original amount r = rate of decrease t = time y = new amount Ex. 1 A cup of coffee contains 130 mg. of caffeine. If caffeine is eliminated from the body at a rate of 11% per hour, how long will it take for half of this caffeine to be eliminated from a person’s body? 11% indicates that it is fixed-rate decay. y = a(1 – r)t a = 130 65 = 130(1 – 0. 11)t r = 0. 11 y = 65 t = ? ? ?

Decay: 1. Fixed rate: y = a(1 – r)t where a = original amount r = rate of decrease t = time y = new amount Ex. 1 A cup of coffee contains 130 mg. of caffeine. If caffeine is eliminated from the body at a rate of 11% per hour, how long will it take for half of this caffeine to be eliminated from a person’s body? 11% indicates that it is fixed-rate decay. y = a(1 – r)t a = 130 65 = 130(1 – 0. 11)t r = 0. 11 65 = 130(0. 89)t y = 65 t = ? ? ?

Decay: 1. Fixed rate: y = a(1 – r)t where a = original amount r = rate of decrease t = time y = new amount Ex. 1 A cup of coffee contains 130 mg. of caffeine. If caffeine is eliminated from the body at a rate of 11% per hour, how long will it take for half of this caffeine to be eliminated from a person’s body? 11% indicates that it is fixed-rate decay. y = a(1 – r)t a = 130 65 = 130(1 – 0. 11)t r = 0. 11 65 = 130(0. 89)t y = 65 0. 5 = (0. 89)t t = ? ? ?

Decay: 1. Fixed rate: y = a(1 – r)t where a = original amount r = rate of decrease t = time y = new amount Ex. 1 A cup of coffee contains 130 mg. of caffeine. If caffeine is eliminated from the body at a rate of 11% per hour, how long will it take for half of this caffeine to be eliminated from a person’s body? 11% indicates that it is fixed-rate decay. y = a(1 – r)t a = 130 65 = 130(1 – 0. 11)t r = 0. 11 65 = 130(0. 89)t y = 65 0. 5 = (0. 89)t t = ? ? ? log(0. 5) = log(0. 89)t

Decay: 1. Fixed rate: where y = a(1 – r)t a = original amount r = rate of decrease t = time y = new amount Ex. 1 A cup of coffee contains 130 mg. of caffeine. If caffeine is eliminated from the body at a rate of 11% per hour, how long will it take for half of this caffeine to be eliminated from a person’s body? 11% indicates that it is fixed-rate decay. y = a(1 – r)t a = 130 65 = 130(1 – 0. 11)t r = 0. 11 65 = 130(0. 89)t y = 65 0. 5 = (0. 89)t t = ? ? ? log(0. 5) = log(0. 89)t log(0. 5) = tlog(0. 89) Power Property

Decay: 1. Fixed rate: where y = a(1 – r)t a = original amount r = rate of decrease t = time y = new amount Ex. 1 A cup of coffee contains 130 mg. of caffeine. If caffeine is eliminated from the body at a rate of 11% per hour, how long will it take for half of this caffeine to be eliminated from a person’s body? 11% indicates that it is fixed-rate decay. y = a(1 – r)t a = 130 65 = 130(1 – 0. 11)t r = 0. 11 65 = 130(0. 89)t y = 65 0. 5 = (0. 89)t t = ? ? ? log(0. 5) = log(0. 89)t log(0. 5) = tlog(0. 89) Power Property log(0. 5) = t log(0. 89)

Decay: 1. Fixed rate: where y = a(1 – r)t a = original amount r = rate of decrease t = time y = new amount Ex. 1 A cup of coffee contains 130 mg. of caffeine. If caffeine is eliminated from the body at a rate of 11% per hour, how long will it take for half of this caffeine to be eliminated from a person’s body? 11% indicates that it is fixed-rate decay. y = a(1 – r)t a = 130 65 = 130(1 – 0. 11)t r = 0. 11 65 = 130(0. 89)t y = 65 0. 5 = (0. 89)t t = ? ? ? log(0. 5) = log(0. 89)t log(0. 5) = tlog(0. 89) Power Property log(0. 5) = t log(0. 89) 5. 9480 ≈ t

2. Natural rate:

2. Natural rate: y = ae-kt

2. Natural rate: y = ae-kt a = original amount k = constant of variation t = time y = new amount

2. Natural rate: y = ae-kt a = original amount k = constant of variation t = time y = new amount Ex. 2 Determine the half-life of Carbon-14 if it’s constant of variation is 0. 00012.

2. Natural rate: y = ae-kt a = original amount k = constant of variation t = time y = new amount Ex. 2 Determine the half-life of Carbon-14 if it’s constant of variation is 0. 00012. *No rate given so must be ‘Natural. ’

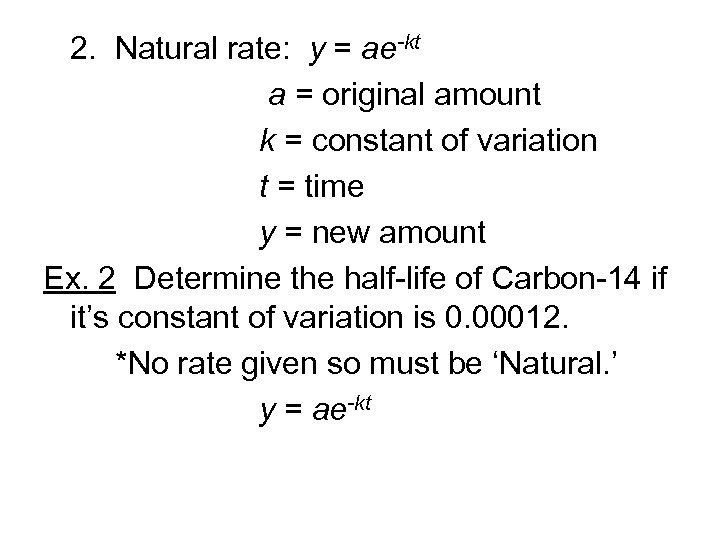2. Natural rate: y = ae-kt a = original amount k = constant of variation t = time y = new amount Ex. 2 Determine the half-life of Carbon-14 if it’s constant of variation is 0. 00012. *No rate given so must be ‘Natural. ’ y = ae-kt

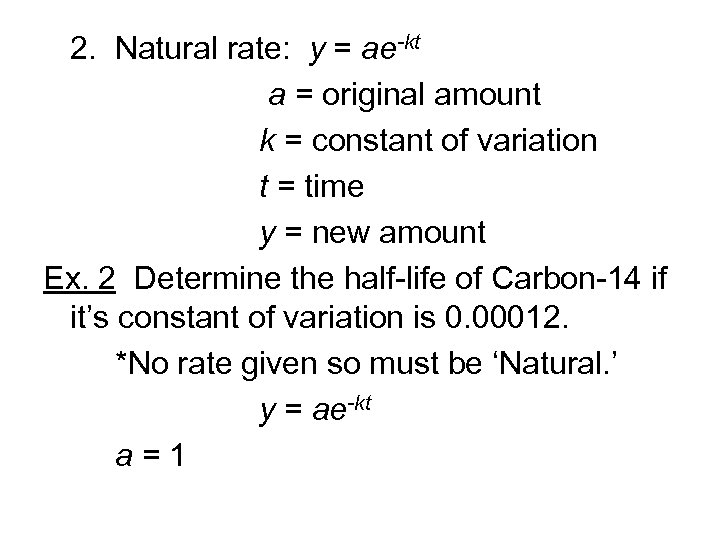2. Natural rate: y = ae-kt a = original amount k = constant of variation t = time y = new amount Ex. 2 Determine the half-life of Carbon-14 if it’s constant of variation is 0. 00012. *No rate given so must be ‘Natural. ’ y = ae-kt a=1

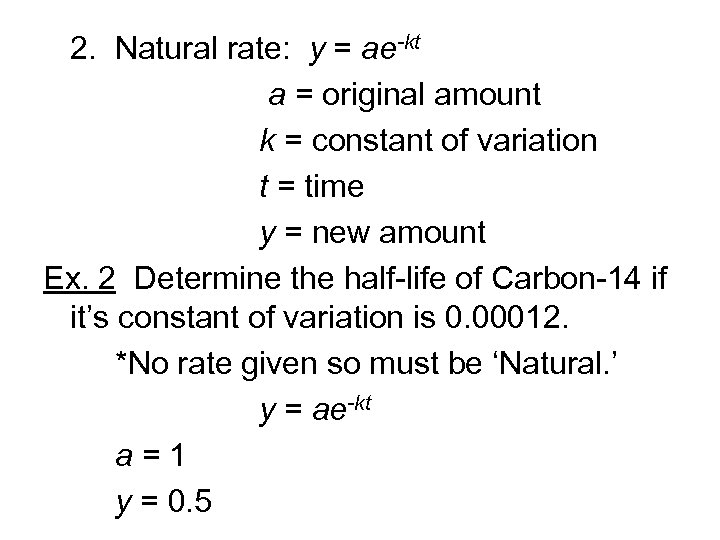2. Natural rate: y = ae-kt a = original amount k = constant of variation t = time y = new amount Ex. 2 Determine the half-life of Carbon-14 if it’s constant of variation is 0. 00012. *No rate given so must be ‘Natural. ’ y = ae-kt a=1 y = 0. 5

2. Natural rate: y = ae-kt a = original amount k = constant of variation t = time y = new amount Ex. 2 Determine the half-life of Carbon-14 if it’s constant of variation is 0. 00012. *No rate given so must be ‘Natural. ’ y = ae-kt a=1 y = 0. 5 k = 0. 00012

2. Natural rate: y = ae-kt a = original amount k = constant of variation t = time y = new amount Ex. 2 Determine the half-life of Carbon-14 if it’s constant of variation is 0. 00012. *No rate given so must be ‘Natural. ’ y = ae-kt a=1 y = 0. 5 k = 0. 00012 t = ? ? ?

2. Natural rate: y = ae-kt a = original amount k = constant of variation t = time y = new amount Ex. 2 Determine the half-life of Carbon-14 if it’s constant of variation is 0. 00012. *No rate given so must be ‘Natural. ’ y = ae-kt a=1 0. 5 = 1 e-0. 00012 t y = 0. 5 k = 0. 00012 t = ? ? ?

2. Natural rate: y = ae-kt a = original amount k = constant of variation t = time y = new amount Ex. 2 Determine the half-life of Carbon-14 if it’s constant of variation is 0. 00012. *No rate given so must be ‘Natural. ’ y = ae-kt a=1 0. 5 = 1 e-0. 00012 t y = 0. 5 = e-0. 00012 t k = 0. 00012 t = ? ? ?

2. Natural rate: y = ae-kt a = original amount k = constant of variation t = time y = new amount Ex. 2 Determine the half-life of Carbon-14 if it’s constant of variation is 0. 00012. *No rate given so must be ‘Natural. ’ y = ae-kt a=1 0. 5 = 1 e-0. 00012 t y = 0. 5 = e-0. 00012 t k = 0. 00012 ln(0. 5) = ln e-0. 00012 t t = ? ? ?

2. Natural rate: y = ae-kt a = original amount k = constant of variation t = time y = new amount Ex. 2 Determine the half-life of Carbon-14 if it’s constant of variation is 0. 00012. *No rate given so must be ‘Natural. ’ y = ae-kt a=1 0. 5 = 1 e-0. 00012 t y = 0. 5 = e-0. 00012 t k = 0. 00012 ln(0. 5) = ln e-0. 00012 t t = ? ? ? ln(0. 5) = -0. 00012 t

2. Natural rate: y = ae-kt a = original amount k = constant of variation t = time y = new amount Ex. 2 Determine the half-life of Carbon-14 if it’s constant of variation is 0. 00012. *No rate given so must be ‘Natural. ’ y = ae-kt a=1 0. 5 = 1 e-0. 00012 t y = 0. 5 = e-0. 00012 t k = 0. 00012 ln(0. 5) = ln e-0. 00012 t t = ? ? ? ln(0. 5) = -0. 00012 t ln(0. 5) = t -0. 00012

2. Natural rate: y = ae-kt a = original amount k = constant of variation t = time y = new amount Ex. 2 Determine the half-life of Carbon-14 if it’s constant of variation is 0. 00012. *No rate given so must be ‘Natural. ’ y = ae-kt a=1 0. 5 = 1 e-0. 00012 t y = 0. 5 = e-0. 00012 t k = 0. 00012 ln(0. 5) = ln e-0. 00012 t t = ? ? ? ln(0. 5) = -0. 00012 t ln(0. 5) = t -0. 00012 5, 776 ≈ t

2. Natural rate: y = ae-kt a = original amount k = constant of variation t = time y = new amount Ex. 2 Determine the half-life of Carbon-14 if it’s constant of variation is 0. 00012. *No rate given so must be ‘Natural. ’ y = ae-kt a=1 0. 5 = 1 e-0. 00012 t y = 0. 5 = e-0. 00012 t k = 0. 00012 ln(0. 5) = ln e-0. 00012 t t = ? ? ? ln(0. 5) = -0. 00012 t ln(0. 5) = t -0. 00012 5, 776 ≈ t *It takes about 5, 776 years for Carbon-14 to decay to half of it’s original amount.

Growth:

Growth: 1. Fixed Rate:

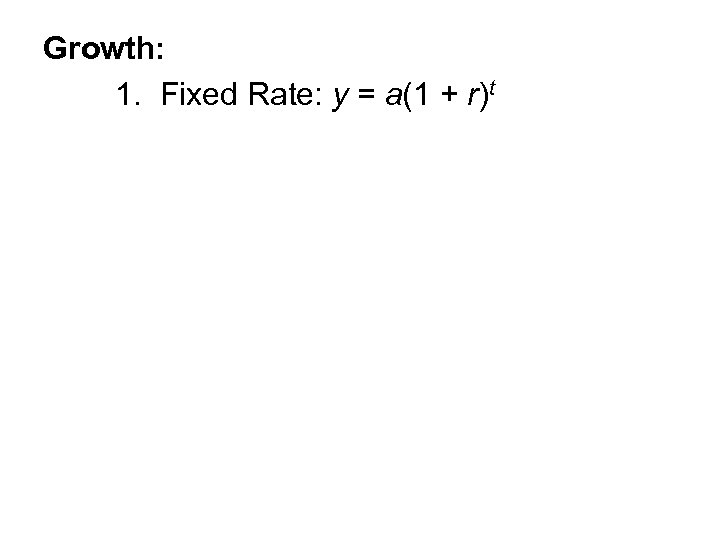Growth: 1. Fixed Rate: y = a(1 + r)t

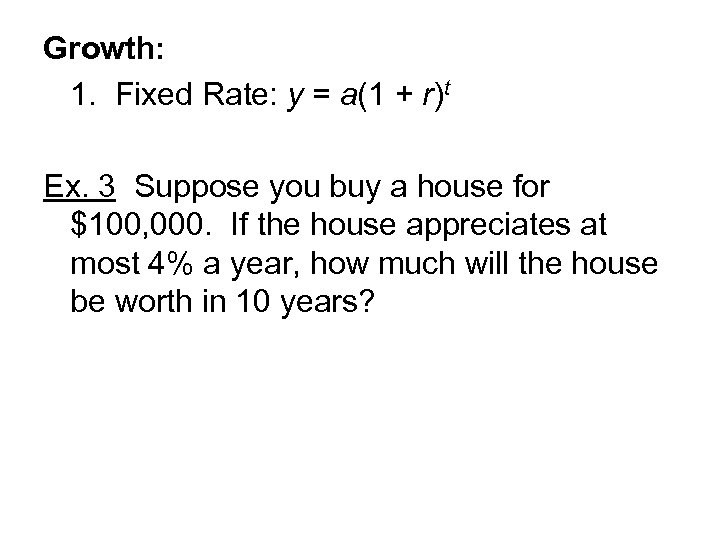Growth: 1. Fixed Rate: y = a(1 + r)t Ex. 3 Suppose you buy a house for $100, 000. If the house appreciates at most 4% a year, how much will the house be worth in 10 years?

Growth: 1. Fixed Rate: y = a(1 + r)t Ex. 3 Suppose you buy a house for $100, 000. If the house appreciates at most 4% a year, how much will the house be worth in 10 years? y = a(1 + r)t

Growth: 1. Fixed Rate: y = a(1 + r)t Ex. 3 Suppose you buy a house for $100, 000. If the house appreciates at most 4% a year, how much will the house be worth in 10 years? y = a(1 + r)t y = 100, 000(1 + 0. 04)10

Growth: 1. Fixed Rate: y = a(1 + r)t Ex. 3 Suppose you buy a house for $100, 000. If the house appreciates at most 4% a year, how much will the house be worth in 10 years? y = a(1 + r)t y = 100, 000(1 + 0. 04)10 y = 100, 000(1. 04)10

Growth: 1. Fixed Rate: y = a(1 + r)t Ex. 3 Suppose you buy a house for $100, 000. If the house appreciates at most 4% a year, how much will the house be worth in 10 years? y = a(1 + r)t y = 100, 000(1 + 0. 04)10 y = 100, 000(1. 04)10 y = $148, 024. 43

2. Natural Rate:

2. Natural Rate: y = aekt

2. Natural Rate: y = aekt Ex. 4 The population of Indianapolis, IN was 781, 870 in 2000. It then rose to 784, 118 by 2005.

2. Natural Rate: y = aekt Ex. 4 The population of Indianapolis, IN was 781, 870 in 2000. It then rose to 784, 118 by 2005. a. Write an exponential growth equation for the data where t is the number of years since 2000.

2. Natural Rate: y = aekt Ex. 4 The population of Indianapolis, IN was 781, 870 in 2000. It then rose to 784, 118 by 2005. a. Write an exponential growth equation for the data where t is the number of years since 2000. y = aekt

2. Natural Rate: y = aekt Ex. 4 The population of Indianapolis, IN was 781, 870 in 2000. It then rose to 784, 118 by 2005. a. Write an exponential growth equation for the data where t is the number of years since 2000. y = aekt 784, 118 = 781, 870 e 5 k

2. Natural Rate: y = aekt Ex. 4 The population of Indianapolis, IN was 781, 870 in 2000. It then rose to 784, 118 by 2005. a. Write an exponential growth equation for the data where t is the number of years since 2000. y = aekt 784, 118 = 781, 870 e 5 k 1. 0029 = e 5 k

2. Natural Rate: y = aekt Ex. 4 The population of Indianapolis, IN was 781, 870 in 2000. It then rose to 784, 118 by 2005. a. Write an exponential growth equation for the data where t is the number of years since 2000. y = aekt 784, 118 = 781, 870 e 5 k 1. 0029 = e 5 k ln(1. 0029) = ln e 5 k

2. Natural Rate: y = aekt Ex. 4 The population of Indianapolis, IN was 781, 870 in 2000. It then rose to 784, 118 by 2005. a. Write an exponential growth equation for the data where t is the number of years since 2000. y = aekt 784, 118 = 781, 870 e 5 k 1. 0029 = e 5 k ln(1. 0029) = ln e 5 k ln(1. 0029) = 5 k

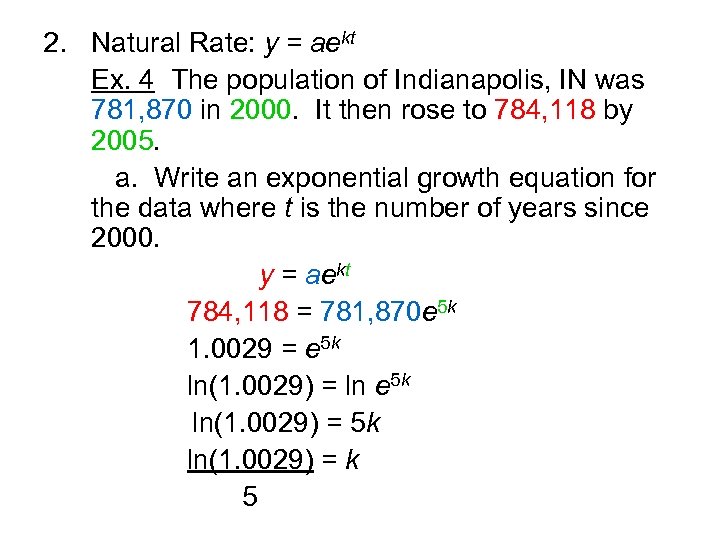2. Natural Rate: y = aekt Ex. 4 The population of Indianapolis, IN was 781, 870 in 2000. It then rose to 784, 118 by 2005. a. Write an exponential growth equation for the data where t is the number of years since 2000. y = aekt 784, 118 = 781, 870 e 5 k 1. 0029 = e 5 k ln(1. 0029) = ln e 5 k ln(1. 0029) = k 5

2. Natural Rate: y = aekt Ex. 4 The population of Indianapolis, IN was 781, 870 in 2000. It then rose to 784, 118 by 2005. a. Write an exponential growth equation for the data where t is the number of years since 2000. y = aekt 784, 118 = 781, 870 e 5 k 1. 0029 = e 5 k ln(1. 0029) = ln e 5 k ln(1. 0029) = k 5 0. 000579 = k

2. Natural Rate: y = aekt Ex. 4 The population of Indianapolis, IN was 781, 870 in 2000. It then rose to 784, 118 by 2005. a. Write an exponential growth equation for the data where t is the number of years since 2000. y = aekt 784, 118 = 781, 870 e 5 k 1. 0029 = e 5 k ln(1. 0029) = ln e 5 k ln(1. 0029) = k 5 0. 000579 = k y = ae 0. 000579 t

b. Use your equation to predict the population of Indianapolis in 2010.

b. Use your equation to predict the population of Indianapolis in 2010. y = ae 0. 000579 t

Ex. 4 The population of Indianapolis, IN was 781, 870 in 2000. It then rose to 784, 118 by 2005. b. Use your equation to predict the population of Indianapolis in 2010. y = ae 0. 000579 t y = 781, 870 e 0. 000579(10)

Ex. 4 The population of Indianapolis, IN was 781, 870 in 2000. It then rose to 784, 118 by 2005. b. Use your equation to predict the population of Indianapolis in 2010. y = ae 0. 000579 t y = 781, 870 e 0. 000579(10) y ≈ 786, 410

Ex. 4 The population of Indianapolis, IN was 781, 870 in 2000. It then rose to 784, 118 by 2005. b. Use your equation to predict the population of Indianapolis in 2010. y = ae 0. 000579 t y = 781, 870 e 0. 000579(10) y ≈ 786, 410 Info obtained from http: //www. idcide. com/citydata/in/india napolis. htm