8 2 Exponential Decay P 474 Exponential

8. 2 Exponential Decay P. 474

Exponential Decay Has the same form as growth functions f(x) = abx Where a > 0 BUT: 0 < b < 1 (a fraction between 0 & 1)

Recognizing growth and decay functions State whether f(x) is an exponential growth or decay function f(x) = 5(2/3)x b=2/3, 01 it is a growth function. f(x) = 10(3)-x rewrite as f(x)=10(1/3)x so it is decay

Recall from 8. 1: The graph of y= abx Passes thru the point (0, a) (the y intercept is a) The x-axis is the asymptote of the graph a tells you up or down D is all reals (the Domain) R is y>0 if a>0 and y<0 if a<0 (the Range)

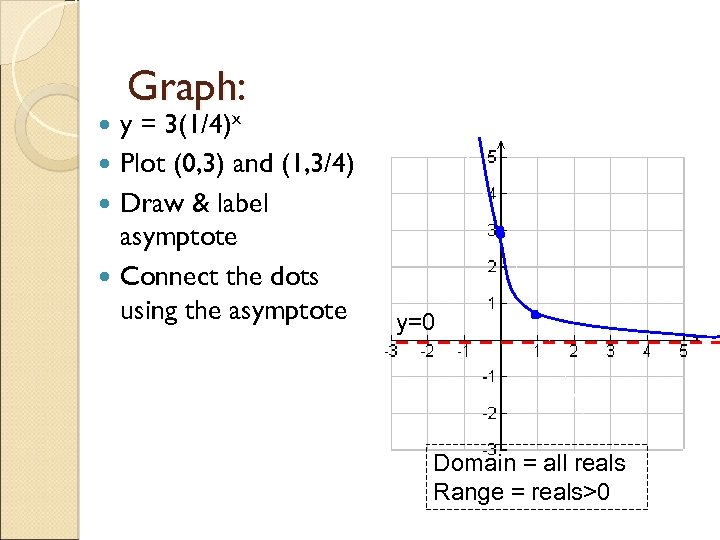Graph: y = 3(1/4)x Plot (0, 3) and (1, 3/4) Draw & label asymptote Connect the dots using the asymptote y=0 Domain = all reals Range = reals>0

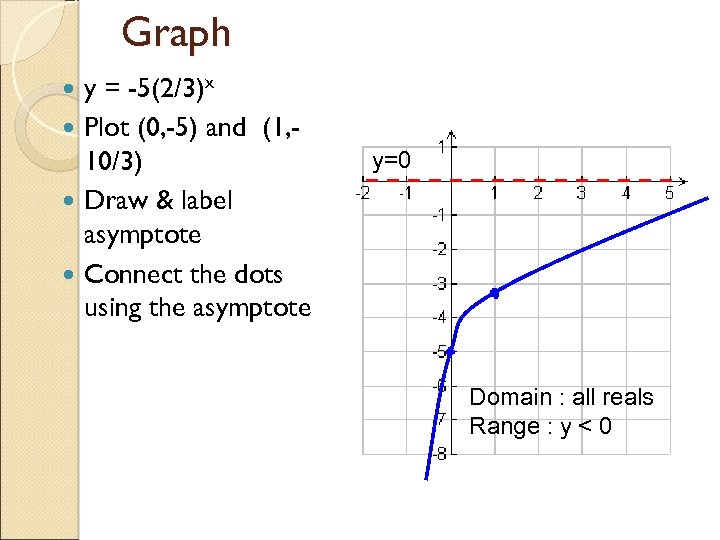Graph y = -5(2/3)x Plot (0, -5) and (1, 10/3) Draw & label asymptote Connect the dots using the asymptote y=0 Domain : all reals Range : y < 0

Now remember: To graph a general Exponential Function: y = a bx-h + k Sketch y = a bx h= ? ? ? k= ? ? ? Move your 2 points h units left or right …and k units up or down Then sketch the graph with the 2 new points.

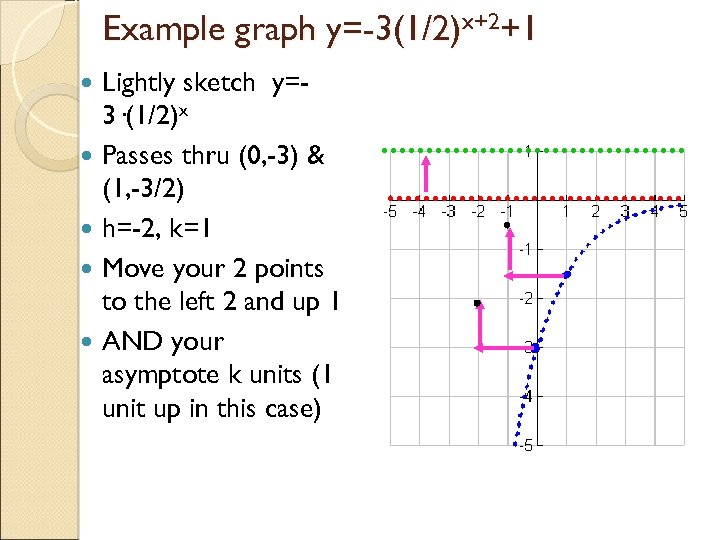Example graph y=-3(1/2)x+2+1 Lightly sketch y=3·(1/2)x Passes thru (0, -3) & (1, -3/2) h=-2, k=1 Move your 2 points to the left 2 and up 1 AND your asymptote k units (1 unit up in this case)

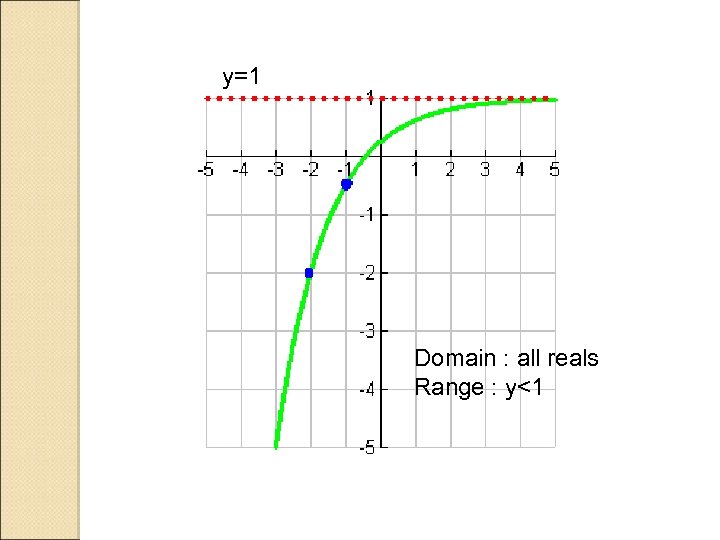y=1 Domain : all reals Range : y<1

Using Exponential Decay Models When a real life quantity decreases by fixed percent each year (or other time period), the amount y of the quantity after t years can be modeled by: y = a(1 -r)t Where a is the initial amount and r is the percent decrease expressed as a decimal. The quantity 1 -r is called the decay factor

Ex: Buying a car! You buy a new car for $24, 000. The value y of this car decreases by 16% each year. Write an exponential decay model for the value of the car. Use the model to estimate the value after 2 years. Graph the model. Use the graph to estimate when the car will have a value of $12, 000.

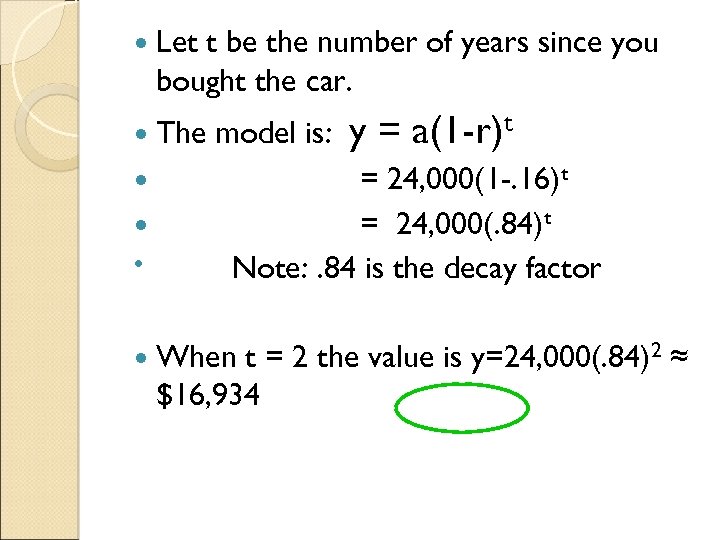Let t be the number of years since you bought the car. The model is: y = a(1 -r)t = 24, 000(1 -. 16)t = 24, 000(. 84)t Note: . 84 is the decay factor When t = 2 the value is y=24, 000(. 84)2 ≈ $16, 934

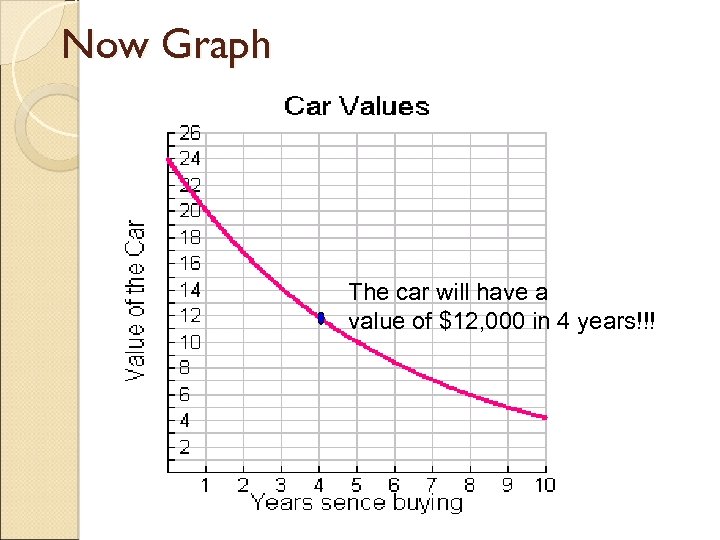Now Graph The car will have a value of $12, 000 in 4 years!!!