7 УКАЗАТЕЛИ СПИСКИ ДЕРЕВЬЯ Программирование списочных и древовидных

7 УКАЗАТЕЛИ СПИСКИ ДЕРЕВЬЯ Программирование списочных и древовидных структур. Запись алгоритмов формирования и обработки линейного списка (бинарного дерева – на выбор)

Списком называется упорядоченное множество, состоящее из переменного числа элементов, к которым применимы операции включения, исключения. Список, отражающий отношения соседства между элементами, называется линейным. Если ограничения на длину списка не допускаются, то список представляется в памяти в виде связной структуры. Линейные связные списки являются простейшими динамическими структурами данных. Графически связи в списках удобно изображать с помощью стрелок. Если компонента не связана ни с какой другой, то в поле указателя записывают значение, не указывающее ни на какой элемент. Такая ссылка обозначается специальным именем - nil.

СТРУКТУРЫ С УКАЗАТЕЛЯМИ (СПИСКИ) ЭЛЕМЕНТ info ОПИСАНИЯ ЭЛЕМЕНТА СПИСКА МОДУЛЬ Fortran module eni type EL 1 real val type(EL 1), pointer : : next end type EL 1 end module eni «хвост» Top info Тип и переменные PASCAL Type El 1 = ^el; el=record val: real; next : El 1 end; var p, p 0, first, last : El 1; ОДНОСВЯЗНЫЙ СПИСОК info

ОДНОСВЯЗНЫЙ СПИСОК И ЕГО СОРТИРОВКА program SP_1 use eni use msflib type(EL 1), pointer : : top, current, p 1 integer n, i; real rnd, tmp do; print '(a, $)', 'Bb n '; read *, n nullify(top)! НАЧАЛО СПИСКА do i=1, n ! Цикл заполнения call random(rnd) allocate(current) !новый элемент current = EL 1(INT(100*rnd), top) top=>current enddo current => top ! ПЕЧАТЬ с Хвоста do while(associated(current)) print '(f 8. 0, $)', current. val current =>current. next end do; print *

(продолжение программы) print *, '===== SORTING ============' current => top do while(associated(current. next)) !цикл до предпоследнего p 1=>current. next !цикл до последнего do while(associated(p 1)) if(current. val>p 1. val)then tmp = current. val = p 1. val !обмен p 1. val = tmp endif p 1 =>p 1. next enddo current => current. next enddo

(ОКОНЧАНИЕ ПРОГРАММЫ) ! ПЕЧАТЬ с ХВОСТА current => top do while(associated(current)) print '(f 8. 0, $)', current. val current =>current. next end do print * current => top ! ОСВОБОЖДЕНИЕ ПАМЯТИ do while(associated(top)) top=>current. next deallocate(current) current => top enddo if(getchar. QQ()==CHAR(27))Stop enddo end program

! ОДНОСВЯЗНЫЙ СПИСОК И ЕГО МЕТОДЫ (SUBROUTINES) module elem ! ТИП Элемента списка type EL 1 real rv integer iv !НОМЕР ЭЛ-ТА type(EL 1), pointer : : next end type EL 1 end module elem program SP_1 use elem use msflib type(EL 1), pointer : : p, Xb, curr, p 1 integer n do; call clearscreen($gclearscreen)

ВВОД ПАРАМЕТРОВ И ВЫЗОВ МЕТОДОВ print '(a, $)', 'Bb n '; read *, n call New_sp 1() !Формирование call View(Xb) !Просмотр print *, 'CHANGE 5 -th' call change(333. , 5); call View(Xb) ! Изменение 5 -го print *, 'DELETE 7 -th' call Delem(7); call View(Xb) !Удаление 7 -го print *, 'INSERT after 8 -th' call Inselem(777. , 8); call View(Xb) ! Вставка после 8 -го call Free_sp 1(Xb) ! Освобождение if(getchar. QQ()==CHAR(27))Stop enddo

МЕТОДЫ CONTAINS Subroutine New_Sp 1() !ФОРМИРОВАНИЕ integer i real rnd nullify(Xb); do i=1, n call random(rnd) allocate(p); p=EL 1(100*rnd, i, Xb); Xb=>p; enddo end subroutine New_Sp 1 Subroutine View(Xb) !ПЕЧАТЬ type(EL 1), pointer : : Xb p=>Xb do while (associated(p)) print '(i 4, f 6. 1, $)', p. iv, p. rv p=>p. next enddo print * end subroutine View

МЕТОДЫ subroutine Change (val, ind) !изменить эл-т ind integer ind; real val p=>Xb; do if(p. iv==ind)exit p=>p. next enddo p. rv = val end subroutine Change subroutine Delem(ind) !удалить эл-т ind integer ind p =>Xb; if(p. iv==ind)then !удаление хвоста Xb=>p. next; deallocate(p); return endif curr=>p. next; do while(associated(curr)) if(curr. iv==ind)then !удаление из середины p. next=>curr. next; deallocate(curr); return endif p=>p. next; curr=>p. next !сдвиг по циклу enddo end subroutine Delem

МЕТОД ДОБАВЛЕНИЯ ЭЛЕМЕНТА subroutine Ins. Elem(val, ind) integer ind real val if(Xb. iv==ind)then ! Добавление в хвост allocate(p); p=EL 1(val, ind+1, Xb); Xb=>p; return endif p=>Xb; curr=>p. next !Вилка поиска места do while(associated(curr)) if(curr. iv==ind)then allocate(p 1); p 1=EL 1(val, ind+1, curr); p. next=>p 1; return endif p=>p. next; curr=>p. next !Сдвиг вилки поиска enddo end subroutine Ins. Elem

МЕТОД ОСВОБОЖДЕНИЯ ПАМЯТИ subroutine Free_Sp 1(Xb) type (EL 1), pointer : : Xb p =>Xb do while(associated(Xb)) Xb=>p. next deallocate(p) p => Xb enddo end subroutine Free_Sp 1 end program

Однако, обработка односвязного списка не всегда удобна, так как отсутствует возможность продвижения в противоположную сторону. Такую возможность обеспечивает двухсвязный список, каждый элемент которого содержит два указателя: на следующий и предыдущий элементы списка. Структура линейного двухсвязного списка приведена на рисунке, где поле NEXT - указатель на следующий элемент, поле PREV –(previous) указатель на предыдущий элемент. В крайних элементах соответствующие указатели должны содержать nil

элемент двухсвязного списка (dll - double linked list) type dllptr = ^dlltype; { указатель в двухсвязном списке } dlltype = record { элемент односвязного списка } inf : data; { информационная часть } next : dllptr; { указатель на следующий элемент (вперед) } prev : dllptr; { указатель на предыдущий элемент (назад) } end; любая структура информационной части списка: type data =. . . ;

Перебор элементов списка Эта операция, возможно, чаще других выполняется над линейными списками. При ее выполнении осуществляется последовательный доступ к элементам списка - ко всем до конца списка или до нахождения искомого элемента. В двухсвязном списке возможен перебор как в прямом направлении (он выглядит точно так же, как и перебор в односвязном списке), так и в обратном. В последнем случае параметром процедуры должен быть tail - указатель на конец списка, и переход к следующему элементу должен осуществляться по указателю назад

Перебор односвязного списка Procedure Look. Sll(head : sllptr); { head - указатель на начало списка } var cur : sllptr; { адрес текущего элемента } begin cur: =head; { 1 -й элемент списка назначается текущим } while cur <> nil do begin < обработка cur^. inf > {обрабатывается информационная часть того эл-та, на который указывает cur. Обработка может состоять в: печати содержимого инф. части; модификации полей инф. части; сравнения полей инф. части с образцом при поиске по ключу; подсчете итераций цикла при поиске по номеру; и т. д. , и т. п. } cur: =cur^. next; { из текущего эл-та выбирается указатель на следующий эл-т и для следующей итерации следующий эл-т становится текущим; если текущий эл-т был последний, то его поле next содержит пустой указатель и, т. обр. в cur запишется nil, что приведет к выходу из цикла при проверке условия while } end;

Вставка элемента в список Procedure Insert. Sll(prev : sllptr; inf : data); { prev - адрес предыдущего эл-та; inf - данные нового эл-та } var cur : sllptr; { адрес нового эл-та } begin { выделение памяти для нового эл-та и запись в его инф. часть } New(cur); cur^. inf: =inf; cur^. next: =prev^. next; { эл-т, следовавший за предыдущим теперь будет следовать за новым } prev^. next: =cur; { новый эл-т следует за предыдущим } end;

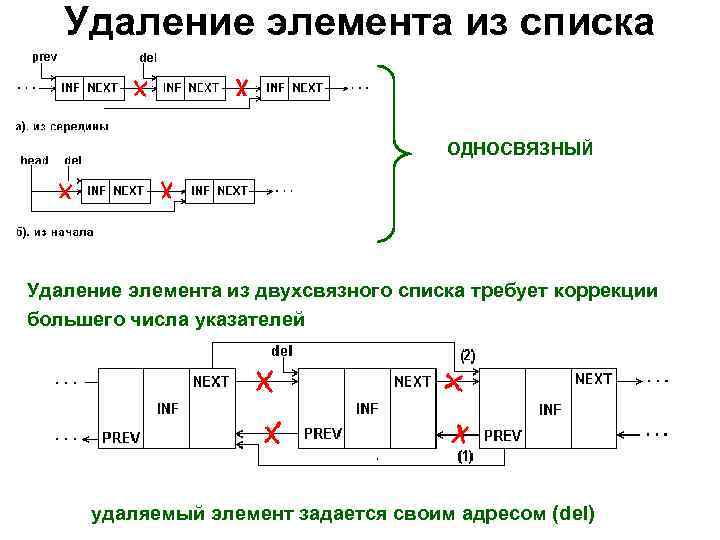Удаление элемента из списка ОДНОСВЯЗНЫЙ Удаление элемента из двухсвязного списка требует коррекции большего числа указателей удаляемый элемент задается своим адресом (del)

Мультисписки В программных системах, обрабатывающих объекты сложной структуры, могут решаться разные подзадачи, каждая из которых требует, возможно, обработки не всего множества объектов, а лишь какого-то его подмножества. Так, например, в автоматизированной системе учета лиц, пострадавших вследствие аварии, каждая запись об одном пострадавшем содержит множество полей в своей информационной части. Решаемые же автоматизированной системой задачи могут потребовать выборки, например: участников аварии; переселенцев; лиц, состоящих на учете; лиц с заболеваниями; и т. д. , и т. п. Для того, чтобы при выборке каждого подмножества не выполнять полный просмотр с отсеиванием записей, к требуемому подмножеству не относящихся, в каждую запись включаются дополнительные поля ссылок, каждое из которых связывает в линейный список элементы соответствующего подмножества. В результате получается многосвязный список или мультисписок, каждый элемент которого может входить одновременно в несколько односвязных списков.

Язык программирования LISP является наиболее развитым и распространенным языком обработки списков. "Идеология" и терминология этого языка в значительной степени повлияла на общепринятые подходы к обработке списков и использовалась и нами в предыдущем изложении. Все данные в LISP представляются в виде списков. LISP обеспечивает базовые функции обработки списков. Помимо чисто списковых операций в языке обеспечиваются операции для выполнения арифметических, логических операций, отношения, присваивания, ввода-вывода и т. д. Операция cond обеспечивает ветвление. Сама LISP-программа представляется как список, записанный в скобочной форме. Элементами простого программного списка является имя операции/функции и ее параметры. Параметрами могут быть в свою очередь обращения к функциям, которые образуют подсписки. Как правило, вся программа на LISP представляет собой единственное обращение к функции с множеством вложенных обращений - рекурсивных или к другим функциям. Поэтому программирование на языке LISP часто называют "функциональным программированием".

ДЕРЕВЬЯ

Структура дерева Опишем дерево как структуру данных формальным языком. В теории графов, дерево — связный неориентированный граф, не содержащий циклов. Древовидная структура — тип организации, в котором каждый объект связан с хотя бы с одним другим. Все цепочки связей в древовидной структуре начинаются от одного корневого объекта, который является родительским по отношению ко всей структуре. Его дочерние объекты в свою очередь могут являться родительскими и содержать ветку дочерних объектов, и так далее.

Какие они бывают? - I Деревья различаются между собой способом представления информации, степенью ветвления, их назначением и различными приёмами, обеспечивающими эффективный поиск, вставку и удаление элементов.

Какие они бывают? - II Рассмотрим наиболее распространённую разновидность деревьев – бинарные деревья, а так же подвид бинарных деревьев – бинарные деревья поиска.

Бинарные деревья

Бинарное дерево – дерево, в котором степень любой вершины не превосходит 3 (для неориентированного графа). Для орграфа: это дерево, максимальная степень исхода любой вершины которого не превосходит 2. В бинарном дереве можно выделить корень и листья. Корень – это выделенная вершина, через которую осуществляется первоначальный доступ к дереву. У каждой вершины бинарного дерева может быть два потомка – левый и правый. Вершины, которые не имеют потомков называются листами. Таким образом становится очевидна рекурсивная природа, бинарного дерева – каждая вершина исходного дерева является корнем своего поддерева.

Рассмотрим структуру бинарного дерева более детально; покажем как реализуется дерево на практике. Пусть i – номер вершины дерева, тогда обозначим её левого и правого потомка как Left(i) и Right(i) соответственно. Чуть позже, более конкретно рассмотрим детали реализации бинарного дерева на языках программирования и покажем как бинарное дерево можно представить в памяти компьютера.

Представление в памяти - I Бинарные деревья можно хранить в памяти различными способами, а именно: использовать явные указатели на потомков, использовать номера элементов вместо указателей или использовать такое свойство бинарного дерева, которое позволяет легко хранить дерево в линейном массиве.

Бинарное дерево поиска (BST)

Деревья поиска представляют собой структуры данных, которые позволяют осуществлять многие операции с динамическими множествами, включая поиск элемента, минимального и максимального значения, предшествующего и последующего элемента, вставку и удаление. Таким образом, дерево поиска может использоваться и как словарь, и как очередь с приоритетами.

Что такое бинарное дерево поиска? Как следует из названия, бинарное дерево поиска в первую очередь является бинарным деревом. Такое дерево может быть представлено при помощи связанной структуры данных, в которой каждый узел является объектом. В дополнение к полям ключа key и сопутствующих данных, каждый узел содержит поля left, right и up, которые указывают на левый, правый и родительские вершины соответственно. Если дочерний или родительский узлы отсутствуют, то соответствующее поле принимает значение NULL(nil, 0 и т. д. )

Ключи бинарного дерева поиска хранятся таким образом, чтобы в любой момент удовлетворять следующему свойству бинарного дерева поиска: Если x – узел бинарного дерева поиска, а узел y находится в левом поддереве x, то key(y) <= key(x). Если узел y находится в правом поддереве x, то key(x) <= key(y). Свойство бинарного дерева поиска позволяет нам вывести все ключи, находящиеся в дереве, в отсортированном порядке с помощью простого рекурсивного алгоритма, называемого симметричным обходом дерева.

Процедура поиска начинается с корня дерева и проходит вниз по дереву. Для каждого узла x на пути вниз ключ key[x] сравнивается с переданным в качестве параметра ключом k. Если ключи одинаковы, поиск завершается. Если k меньше key[x], поиск продолжается в левом поддереве x; если больше – то поиск переходит в правое поддерево. Так, на рисунке для поиска ключа 13 необходимо пройти следующий путь от корня: 15 -> 6 -> 7 -> 13. Узлы, которые проходятся при рекурсивном поиске, образуют нисходящий путь от корня дерева, так что время работы процедуры tree_search равно O(h), h - высота дерева

Предшествующий и последующий элементы Иногда, имея узел в бинарном дереве, требуется определить, какой узел следует за ним в отсортированном порядке, определяемом порядком симметричного обхода бинарного дерева, и какой узел предшествует данному. Если все ключи различны, последующим по отношению к узлу x является узел с наименьшим ключом, большим key(x). Структура бинарного дерева поиска позволяет найти этот узел даже не выполняя сравнение ключей. Приведённая далее реализация возвращает узел, следующий за узлом x в бинарном дереве поиска (если таковой существует) и NULL, если x обладает наибольшим ключом в дереве.

Вставка и удаление Операции вставки и удаления приводят к внесению изменений в динамическое множество, представленное бинарным деревом поиска. Структура данных должна быть изменена таким образом, чтобы отражать эти изменения, но при этом сохранить свойство бинарных деревьев поиска. Вставка нового элемента в бинарное дерево поиска выполняется относительно просто, однако удаление может вызвать некоторые затруднения. .

Вставка Для вставки нового значения v в бинарное дерево поиска воспользуемся процедурой tree_insert. Процедура получает в качестве параметра узел z, у которого key(z)=v, Left(z)=NULL, Right(z)=NULL, после чего она таким образом изменяет дерево и поля z, что z оказывается вставленным в соответствующую позицию в дереве.

Удаление z из бинарного дерева поиска получает в z. Процедура рассматривает три Процедура удаления данного узла качестве аргумента указатель на возможные ситуации: – Если у узла нет дочерних узлов(то просто изменяем его родительский узел p(z), заменяя в нём указатель на z значением NULL) – Если у узла z только один дочерний элемент(то удаляем узел z, создавая новую связь между родительским и дочерним узлом узла z) – Если у узла z две дочерние вершины(то находим следующий за ним узел y, у которого нет левого дочернего узла, убираем его из позиции, где он находился ранее, путём создания новой связи между его родителем и потомком, и заменяем их на узел)

Первый случай

Второй случай

Третий случай

Дерево на Fortran’е (1) ПОСТРОИТЬ ДЕРЕВО и СПИСОК ЛИСТЬЕВ program mytree Up use msflib implicit none type node !Узел дерева integer inf type(node), pointer : : left type(node), pointer : : right type(node), pointer : : Up end type node inf Left Right

Дерево на Fortran’е (2) type L 1 type(node), pointer : : ADDR type (L 1), pointer : : Next end type L 1 Элемент списка адресов листьев ПЕРЕМЕННЫЕ ПРОГРАММЫ integer i, n, k, a(100) real rnd type (node), pointer : : root, Just, TMP, rab. Leaf ! TREE type (L 1), pointer : : Xv, p ! LEAVES

Дерево на Fortran’е (3) НАЧАЛО ПРОГРАММЫ, ВВОД ПАРАМЕТРОВ do call clearscreen($gclearscreen) print '(a$)', 'Bb. n, k ' read *, n, k do i=1, n call random(rnd) a(i)=INT(k*rnd) enddo print *, 'Array : '; print '(i 4$)', a(1: n); print *

Дерево на Fortran’е (4) ! СОЗДАНИЕ ДЕРЕВА Nullify(Root) do i=1, n Root=>Make. Node(a(i), Root) enddo print *, 'Printing TREE‘ ! ПЕЧАТЬ ДЕРЕВА call PRN_Tree(Root); print *

Дерево на Fortran’е (5) ПЕЧАТЬ ДЕРЕВА call PRN_Tree(Root) recursive subroutine PRN_Tree(p) implicit none type(node), pointer: : p if (associated(p)) then call PRN_Tree(p%left) print '(i 4$)', p%inf call PRN_Tree(p%right) endif endsubroutine

Дерево на Fortran’е (6) ! Составляем список листьев и выводим пути : Nullify(Xv) Xv=>List. Leaves(Root, Xv) print *, 'Paths' ! ПУТИ if(. not. associated(Xv))print *, 'Not Leaves' p=>Xv По адресам листьев do while (associated(p)) Rab. Leaf=>p%Addr До корня do while(associated(Rab. Leaf)) Print '(i 4$)', rab. Leaf%inf Rab. Leaf=>Rab. Leaf%Up enddo print * p=>p%Next enddo

Дерево на Fortran’е (7) СПИСОК АДРЕСОВ ЛИСТЬЕВ recursive function List. Leaves(Root, Xv) type(node), pointer: : Root type(L 1), pointer: : List. Leaves, Xv if (. not. Associated(Root))then Nullify(List. Leaves); return endif if(Associated(Root%Left))Xv=>List. Leaves(Root%Left, Xv) if((. not. Associated(Root%Left)). and. & (. not. Associated(Root%Right)))then allocate(p); p%Addr=>Root; p%Next => Xv; Xv=>p endif if(Associated(Root%Right))Xv =>List. Leaves(Root%Right, Xv) List. Leaves=>Xv end function

Дерево на Fortran’е (8) print *, 'Leaves' !ЛИСТЬЯ p=>Xv do while (associated(p)) Rab. Leaf=> p%ADDR Print '(i 4$)', rab. Leaf%inf p=>p%Next enddo print * !КОНЕЦ ЦИКЛА ЗАДАЧИ print *, 'Press any Key or ' if(ichar(getchar. QQ())==27)stop enddo

Дерево на Fortran’е (9) contains function Make. Node (a, Root) Type(node), pointer : : make. Node, Root integer a, fl allocate(Just) !New NODE Just%inf = a Nullify(Just%Left) Nullify(Just%Right) if(. not. associated(Root))then ! НОВЫЙ КОРЕНЬ Nullify(Just%Up) Root=>Just Make. Node=> Root return else ! ИСКАТЬ МЕСТО В СУЩЕСТВУЮЩЕМ ДЕРЕВЕ

Дерево на Fortran’е (10) Tmp => Root; fl = 0; do ! ПОИСК МЕСТА НОВОГО УЗЛА if(Just%inf<=Tmp%inf) then if(associated (Tmp%Left))then Tmp=>Tmp%Left else fl =1 endif else; if(associated (Tmp. Right))then Tmp=>Tmp. Right else fl =1 endif; if(fl==1) Exit enddo Just%Up => Tmp if(Just%inf<=Tmp%inf) then ; Tmp%Left=>Just else; Tmp%Right=>Just endif Make. Node=>Root end function

Выполнение программы

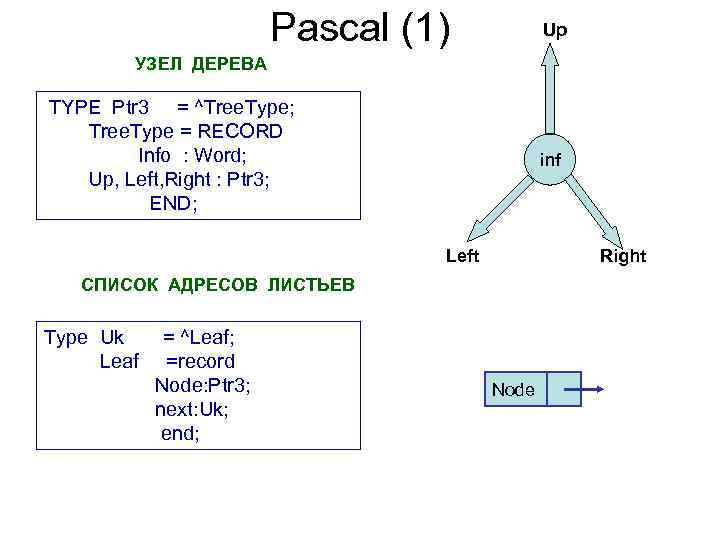Pascal (1) Up УЗЕЛ ДЕРЕВА TYPE Ptr 3 = ^Tree. Type; Tree. Type = RECORD Info : Word; Up, Left, Right : Ptr 3; END; inf Left Right СПИСОК АДРЕСОВ ЛИСТЬЕВ Type Uk Leaf = ^Leaf; =record Node: Ptr 3; next: Uk; end; Node

Pascal (2) Создание узла PROCEDURE Make. Node( x: integer; VAR Tree. Root: Ptr 3); var Just, Tmp : Ptr 3; Enough : Boolean; BEGIN New(Just); Just^. Info: =x; Just^. Left: =NIL; Just^. Right: =NIL; IF Tree. Root=nil THEN BEGIN // Первый узел дерева Just^. Up: =NIL; Tree. Root: =Just; END ELSE BEGIN Tmp: =Tree. Root; Enough: =FALSE; п REPEAT о IF Just^. Info<=Tmp^. Info THEN BEGIN и IF Tmp^. Left<>NIL THEN Tmp: =Tmp^. Left с ELSE Enough: =TRUE; к END ELSE BEGIN IF Tmp^. Right<>NIL THEN Tmp: =Tmp^. Right м ELSE Enough: =TRUE; е END; с UNTIL Enough; т Just^. Up: =Tmp; а IF Just^. Info<=Tmp^. Info THEN Tmp^. Left: =Just ELSE Tmp^. Right: =Just; END; {Make. Node}

Pascal (3) Организовать дерево, вводя целые числа до ввода символа «*» Собрать список адресов листьев. Операции с листьями: Max, произв. , … VAR Tree. Root, rab. Leaf: Ptr 3; Leaves, Xb, Addr : Uk; Mem : Pointer; st : string; a, code : integer; Max : Word; ГЛОБАЛЬНЫЕ ПЕРЕМЕННЫЕ BEGIN Repeat Clr. Scr; //ФОРМИРОВАНИЕ ДЕРЕВА Mark(Mem); //Метка для освобождения дин. памяти Tree. Root: =nil; //КОРЕНЬ Repeat write('Ввести число или * '); Readln(st); if st[1]='*' then break; Val(st, a, code); if code<>0 then Continue; Make. Node(a, Tree. Root); until false;

Pascal (4) Writeln('Упорядоченные узлы'); //ОБХОД ДЕРЕВА Prn. Tree(Tree. Root); writeln; Leaves: =nil; //ФОРМИРОВАНИЕ СПИСКА ЛИСТЬЕВ List. Leaves( Tree. Root, Leaves); Xb: =Leaves; writeln('Пути дерева'); While Xb<>nil do begin // цикл адресов rab. Leaf: =Xb^. Node; while rab. Leaf<>nil do begin write(rab. Leaf^. info: 4); Очередной путь rab. Leaf: =rab. Leaf^. Up; end; writeln; Xb: =Xb^. next; end;

Pascal (5) PROCEDURE Prn. Tree( Root: Ptr 3); {Обход бинарного BEGIN if Root=nil then Exit; IF Root^. Left<>NIL THEN Prn. Tree(Root^. Left); write(Root^. Info: 4); IF Root^. Right<>NIL THEN Prn. Tree(Root^. Right); END; дерева} { СПИСОК АДРЕСОВ ЛИСТЬЕВ} PROCEDURE List. Leaves( Root: Ptr 3; var Leaves: Uk); BEGIN if Root=nil then Exit; IF Root^. Left<>NIL THEN List. Leaves(Root^. Left, Leaves); if(Root^. Left=NIL)and(Root^. Right=NIL) then begin New(Xb); Xb^. Node: =Root; Xb^. next: =Leaves; Leaves: =Xb; end; IF Root^. Right<>NIL THEN List. Leaves(Root^. Right, Leaves); END;

Pascal (6) МАКСИМАЛЬНЫЙ ЛИСТ Max: =0; Xb: =Leaves; writeln('MAX каждого пути'); While Xb<>nil do begin write( MAX(Xb): 4); if Max(Xb)>Max. Max then Max: =Max(Xb); Xb: =Xb^. next; end; Writeln; writeln('Max. Max= ', Max); FUNCTION Max(Addr. Leaf: Uk): Word; Var p: Ptr 3; rab: Word; Begin rab: =0; p: =Addr. Leaf^. Node; while p<>nil do begin if p^. Info>rab then rab: =p^. Info; p: =p^. Up end; Max: =rab; End;

Pascal (7) Xb: =Leaves; writeln('Произведения Путей'); Max: =0; Addr: =Xb; While Xb<>nil do begin write( Product(Xb): 4); if Product(Xb)>Max. Max then begin Addr: =Xb; Max: =Product(Xb) end; Xb: =Xb^. next; end; Writeln; writeln('Max. Product= ', Max); write('Соотв путь->'); rab. Leaf: =Addr^. Node; while rab. Leaf<>nil do begin write(rab. Leaf^. info: 4); rab. Leaf: =rab. Leaf^. Up; end; writeln; Release(Mem); {освобождение дин. памяти} writeln('REPEAT. . . any Key OUT -> ESC'); until Read. Key=#27; END.

Pascal (7) FUNCTION Product(Addr. Leaf: Uk): Word; Var p: Ptr 3; rab: Word; Begin rab: =1; p: =Addr. Leaf^. Node; while p<>nil do begin rab: =rab*p^. Info; p: =p^. Up end; Product: =rab; End;

СБАЛАНСИРОВАННЫЕ ДЕРЕВЬЯ Одной из наиболее часто встречающихся задач является поиск необходимых данных. Существуют различные методы, отличающиеся друг от друга временем поиска, сложностью алгоритмов, размерами требуемой памяти. Обычно стремятся всячески сократить время, затрачиваемое на поиск необходимого элемента. Одним из самых быстрых методов является поиск по упорядоченному бинарному дереву. При удачной структуре дерева время поиска элементов не превышает в среднем log N. Но при неудачной структуре время поиска может значительно возрасти, достигая N2. ( N - число элементов дерева). Одним из методов, улучшающих время поиска в бинарном дереве является создание сбалансированных деревьев обладающих минимальным временем поиска. Одно из определений сбалансированности было дано Адельсоном. Вельским и Ландисом: Дерево является СБАЛАНСИРОВАННЫМ тогда и только тогда, когда для каждого узла высота его двух поддеревьев различается не более чем на 1. Поэтому деревья, удовлетворяющие этому условию, часто называют "АВЛ-деревьями" (по фамилиям их изобретателей).

С тем чтобы предупредить появление несбалансированного дерева, вводится для каждого узла (вершины) дерева показатель сбалансированности, который не может принимать одно из трех значений, левое - (L), правое - (R), сбалансированное - (B), в соответствии со следующими определениями: левое - узел левоперевешивающий, если самый длинный путь по ее левому поддереву на единицу больше самого длинного пути по ее правому поддереву; сбалансированное - узел называется сбалансированный, если равны наиболее длинные пути по обеим ее поддеревьям; правое - узел правоперевешивающий, если самый длинный путь по ее правому поддереву на единицу больше самого длинного пути по ее левому поддереву; В сбалансированном дереве каждый узел должен находится в одном из этих трех состояний. Если в дереве существует узел, для которого это условие несправедливо, такое дерево называется несбалансированным.

ПРИМЕР ПОСТРОЕНИЯ СБАЛАНСИРОВАННОГО ДЕРЕВА Рассмотрим бинарное дерево (а), которое состоит только из двух узлов. Включение ключа 7 дает вначале несбалансированное дерево (т. е. линейный список). Его балансировка требует однократного правого (RR) поворота, давая в результате идеально сбалансированное дерево (b). Последующее включение узлов 2 и 1 дает несбалансированное поддерево с корнем 4. Это поддерево балансируется однократным левым (LL) поворотом (d). Далее включение ключа 3 сразу нарушает критерий сбалансированности в корневом узле 5. Сбалансированность теперь восстанавливается с помощью более сложного двукратного поворота налево и направо (LR); результатом является дерево (e). Теперь при следующем включении потерять сбалансированность может лишь узел 5. Действительно, включение узла 6 должно привести к четвертому виду балансировки: двукратному повороту направо и налево (RL).

The End