 7. Тупики (deadlocks)
7. Тупики (deadlocks)
 7. 1. Определение тупиков • Поток находится в тупике, если он ожидает событие, которое никогда не произойдет. • Событие не может произойти никогда по следующим двум причинам: – не существует потока, который оповещает о наступлении данного события; – такой поток существует, но сам находится в тупике. • Будем считать, что процесс находится в тупике, если находится в тупике хотя бы один поток этого процесса.
7. 1. Определение тупиков • Поток находится в тупике, если он ожидает событие, которое никогда не произойдет. • Событие не может произойти никогда по следующим двум причинам: – не существует потока, который оповещает о наступлении данного события; – такой поток существует, но сам находится в тупике. • Будем считать, что процесс находится в тупике, если находится в тупике хотя бы один поток этого процесса.
 7. 2. Классификация системных ресурсов
7. 2. Классификация системных ресурсов
 Классификация системных ресурсов по доступу • Классификация ресурсов по доступу: – совместно используемые ресурсы; – монопольные ресурсы. • Совместно используемый ресурс может одновременно использоваться несколькими потоками, например, файл. • Монопольный ресурс может быть предоставлен потоку только в монопольное использование, например, принтер.
Классификация системных ресурсов по доступу • Классификация ресурсов по доступу: – совместно используемые ресурсы; – монопольные ресурсы. • Совместно используемый ресурс может одновременно использоваться несколькими потоками, например, файл. • Монопольный ресурс может быть предоставлен потоку только в монопольное использование, например, принтер.
 Классификация ресурсов по способу распределения • Классификация ресурсов по способу распределения: – перераспределяемые (preemptable) ресурсы; – не перераспределяемые (non-preempable) ресурсы. • Перераспределяемый ресурс может быть отобран у потока, владеющего этим ресурсом, и распределен другому потоку, например, страница реальной памяти. • Не перераспределяемый ресурс не может быть отобран у потока, который владеет этим ресурсом, например, принтер.
Классификация ресурсов по способу распределения • Классификация ресурсов по способу распределения: – перераспределяемые (preemptable) ресурсы; – не перераспределяемые (non-preempable) ресурсы. • Перераспределяемый ресурс может быть отобран у потока, владеющего этим ресурсом, и распределен другому потоку, например, страница реальной памяти. • Не перераспределяемый ресурс не может быть отобран у потока, который владеет этим ресурсом, например, принтер.
 Классификация ресурсов по времени существования • Классификация ресурсов по времени существования: – повторно используемые ресурсы; – потребляемые ресурсы. • Повторно используемый ресурс может использоваться потоками многократно, например, принтер. • Потребляемый ресурс может использоваться потоком только один раз, после этого он перестает существовать, например, сообщение из очереди сообщений.
Классификация ресурсов по времени существования • Классификация ресурсов по времени существования: – повторно используемые ресурсы; – потребляемые ресурсы. • Повторно используемый ресурс может использоваться потоками многократно, например, принтер. • Потребляемый ресурс может использоваться потоком только один раз, после этого он перестает существовать, например, сообщение из очереди сообщений.
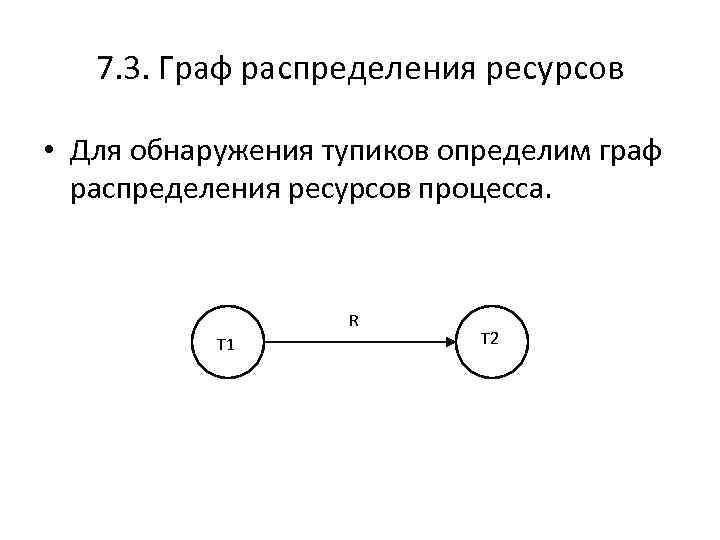 7. 3. Граф распределения ресурсов • Для обнаружения тупиков определим граф распределения ресурсов процесса. R T 1 T 2
7. 3. Граф распределения ресурсов • Для обнаружения тупиков определим граф распределения ресурсов процесса. R T 1 T 2
 – Граф ресурсов процесса – это ориентированный граф, вершины которого обозначают потоки, а дуги интерпретируются следующим образом: • случай повторно используемых ресурсов: поток T 1 запрашивает ресурс R, занятый потоком T 2; • случай потребляемых ресурсов: поток T 1 потребляет ресурс R, произведенный потоком T 2.
– Граф ресурсов процесса – это ориентированный граф, вершины которого обозначают потоки, а дуги интерпретируются следующим образом: • случай повторно используемых ресурсов: поток T 1 запрашивает ресурс R, занятый потоком T 2; • случай потребляемых ресурсов: поток T 1 потребляет ресурс R, произведенный потоком T 2.
 7. 4. Обнаружение тупиков в случае повторно используемых ресурсов • Рассмотрим процесс, в котором потоки используют только повторно используемые ресурсы. • В этом случае поток такого процесса находится в тупике, если он бесконечно долго ждет ресурс, захваченный другим потоком.
7. 4. Обнаружение тупиков в случае повторно используемых ресурсов • Рассмотрим процесс, в котором потоки используют только повторно используемые ресурсы. • В этом случае поток такого процесса находится в тупике, если он бесконечно долго ждет ресурс, захваченный другим потоком.
 • Теорема 1 (Критерий тупика в случае повторно используемых ресурсов). – Процесс, в котором потоки используют только повторно используемые ресурсы, находится в тупике когда граф распределения ресурсов этого процесса содержит цикл.
• Теорема 1 (Критерий тупика в случае повторно используемых ресурсов). – Процесс, в котором потоки используют только повторно используемые ресурсы, находится в тупике когда граф распределения ресурсов этого процесса содержит цикл.
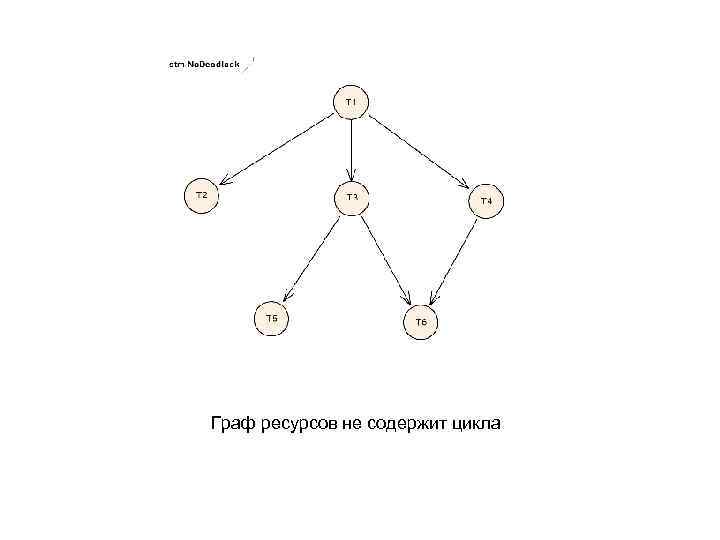 Граф ресурсов не содержит цикла
Граф ресурсов не содержит цикла
 Доказательство • ( ) Доказываем от противного. Пусть процесс находится в тупике. Построим граф G распределения ресурсов этого процесса. Предположим, что этот граф не содержит циклов. Возьмем произвольную вершину v графа G и найдем все пути, началом которых служит эта вершина. Каждый из этих путей не образует цикл (по предположению).
Доказательство • ( ) Доказываем от противного. Пусть процесс находится в тупике. Построим граф G распределения ресурсов этого процесса. Предположим, что этот граф не содержит циклов. Возьмем произвольную вершину v графа G и найдем все пути, началом которых служит эта вершина. Каждый из этих путей не образует цикл (по предположению).
 Потоки, которые являются концами путей, завершат свою работу и освободят захваченные ими ресурсы. Будут разблокированы потоки, которые связаны с концевыми вершинами. Повторяя эти рассуждения, в конце концов получим, что будет разблокирован поток, представленный вершиной v. Получили противоречие с условием, что процесс находится в тупике. Наше предположение неверно и в графе распределения ресурсов есть цикл.
Потоки, которые являются концами путей, завершат свою работу и освободят захваченные ими ресурсы. Будут разблокированы потоки, которые связаны с концевыми вершинами. Повторяя эти рассуждения, в конце концов получим, что будет разблокирован поток, представленный вершиной v. Получили противоречие с условием, что процесс находится в тупике. Наше предположение неверно и в графе распределения ресурсов есть цикл.
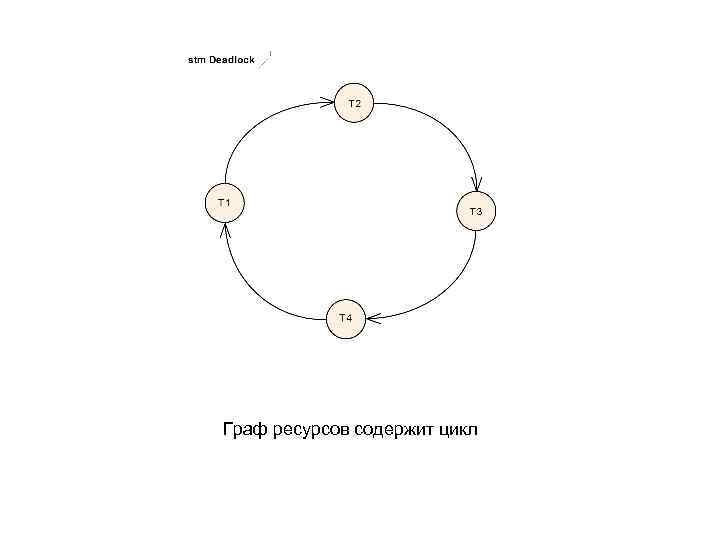 Граф ресурсов содержит цикл
Граф ресурсов содержит цикл
 • ( ) Пусть граф распределения ресурсов содержит цикл: T 1, T 2, …, Tn, T 1. Поток T 1 будет заблокирован до тех пор, пока ресурс, требуемый этим потоком, не будет освобожден потоком T 2. Повторяя эти рассуждения получим, что поток T 1 будет заблокирован до тех пор, пока поток Tn не освободит ресурс, требуемый потоком Tn-1.
• ( ) Пусть граф распределения ресурсов содержит цикл: T 1, T 2, …, Tn, T 1. Поток T 1 будет заблокирован до тех пор, пока ресурс, требуемый этим потоком, не будет освобожден потоком T 2. Повторяя эти рассуждения получим, что поток T 1 будет заблокирован до тех пор, пока поток Tn не освободит ресурс, требуемый потоком Tn-1.
 Но этого не произойдет никогда, т. к. поток Tn ждет ресурс, захваченный самим потоком T 1. Процесс находится в тупике.
Но этого не произойдет никогда, т. к. поток Tn ждет ресурс, захваченный самим потоком T 1. Процесс находится в тупике.
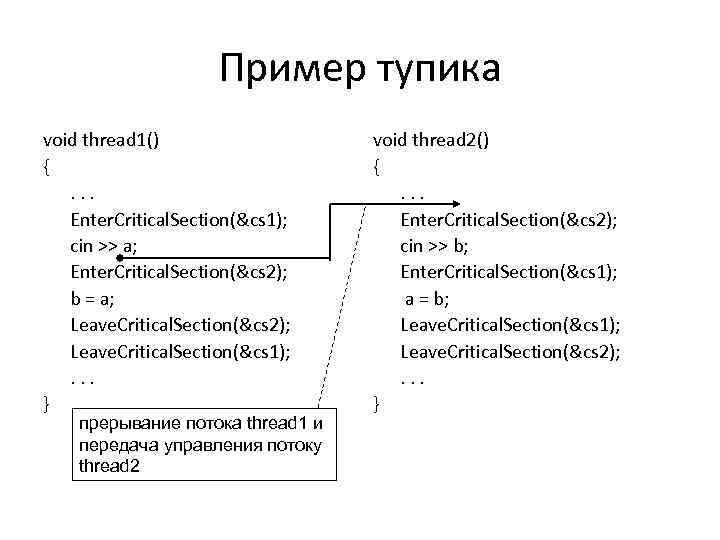 Пример тупика void thread 1() {. . . Enter. Critical. Section(&cs 1); cin >> a; Enter. Critical. Section(&cs 2); b = a; Leave. Critical. Section(&cs 2); Leave. Critical. Section(&cs 1); . . . } прерывание потока thread 1 и передача управления потоку thread 2 void thread 2() {. . . Enter. Critical. Section(&cs 2); cin >> b; Enter. Critical. Section(&cs 1); a = b; Leave. Critical. Section(&cs 1); Leave. Critical. Section(&cs 2); . . . }
Пример тупика void thread 1() {. . . Enter. Critical. Section(&cs 1); cin >> a; Enter. Critical. Section(&cs 2); b = a; Leave. Critical. Section(&cs 2); Leave. Critical. Section(&cs 1); . . . } прерывание потока thread 1 и передача управления потоку thread 2 void thread 2() {. . . Enter. Critical. Section(&cs 2); cin >> b; Enter. Critical. Section(&cs 1); a = b; Leave. Critical. Section(&cs 1); Leave. Critical. Section(&cs 2); . . . }
 7. 5. Обнаружение тупиков в случае потребляемых ресурсов • Рассмотрим процесс, в котором потоки используют только потребляемые ресурсы. • Пусть G – граф распределения ресурсов такого процесса.
7. 5. Обнаружение тупиков в случае потребляемых ресурсов • Рассмотрим процесс, в котором потоки используют только потребляемые ресурсы. • Пусть G – граф распределения ресурсов такого процесса.
 Определение узла • Подграф H графа G называется узлом, если: – через все вершины графа H проходит цикл; – для каждой дуги, связывающей подграф GH с подграфом H, вершина из подграфа GH является началом этой дуги, вершина из подграфа H – концом этой дуги.
Определение узла • Подграф H графа G называется узлом, если: – через все вершины графа H проходит цикл; – для каждой дуги, связывающей подграф GH с подграфом H, вершина из подграфа GH является началом этой дуги, вершина из подграфа H – концом этой дуги.
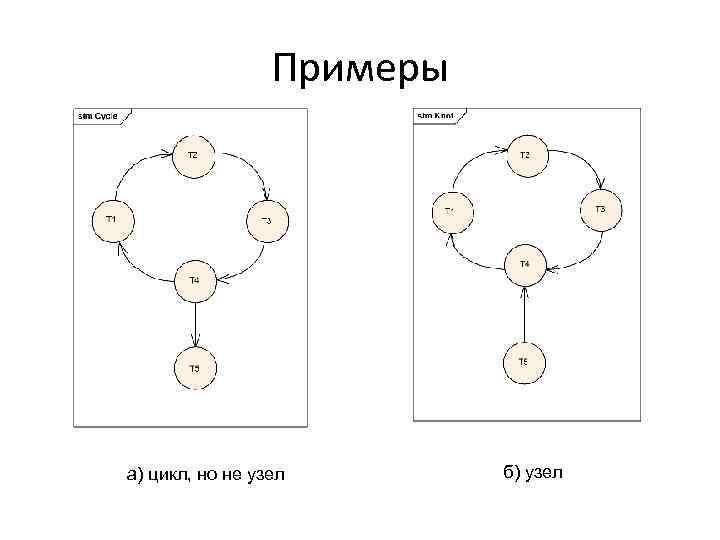 Примеры а) цикл, но не узел б) узел
Примеры а) цикл, но не узел б) узел
 • Теорема 2 (критерий тупика в случае потребляемых ресурсов). – Процесс, в котором потоки используют только потребляемые ресурсы, находится в тупике если граф распределения ресурсов этого процесса содержит узел. • Доказывается теорема аналогично теореме 1.
• Теорема 2 (критерий тупика в случае потребляемых ресурсов). – Процесс, в котором потоки используют только потребляемые ресурсы, находится в тупике если граф распределения ресурсов этого процесса содержит узел. • Доказывается теорема аналогично теореме 1.
 7. 6. Восстановление после обнаружения тупика
7. 6. Восстановление после обнаружения тупика
 Три подхода к восстановлению процесса • После обнаружения тупика должно быть выполнено восстановление процесса, которое заключается в разблокировании потоков этого процесса. • Существуют три подхода к восстановлению процесса: 1. Перераспределение ресурсов (preemption). 2. Прекращение работы заблокированных потоков (termination). 3. Откат на контрольную точку (rollback).
Три подхода к восстановлению процесса • После обнаружения тупика должно быть выполнено восстановление процесса, которое заключается в разблокировании потоков этого процесса. • Существуют три подхода к восстановлению процесса: 1. Перераспределение ресурсов (preemption). 2. Прекращение работы заблокированных потоков (termination). 3. Откат на контрольную точку (rollback).
 Перераспределение ресурсов • Этот подход к восстановлению процесса – самый лучший, но редко может быть осуществим на практике по причине невозможности перераспределения ресурсов.
Перераспределение ресурсов • Этот подход к восстановлению процесса – самый лучший, но редко может быть осуществим на практике по причине невозможности перераспределения ресурсов.
 Прекращение работы заблокированных потоков • Этот подход к восстановлению процесса – самый плохой, так как нарушается целостность обрабатываемой информации. • Однако, этот подход можно применять в случае, если потерянная информация не является существенной.
Прекращение работы заблокированных потоков • Этот подход к восстановлению процесса – самый плохой, так как нарушается целостность обрабатываемой информации. • Однако, этот подход можно применять в случае, если потерянная информация не является существенной.
 Откат на контрольную точку • Этот подход к восстановлению процесса применяется наиболее часто. Но при реализации этого подхода должны быть решены две проблемы: – корректное освобождение ресурсов, захваченных заблокированным потоком; – восстановление информации на момент, предшествующий тупику.
Откат на контрольную точку • Этот подход к восстановлению процесса применяется наиболее часто. Но при реализации этого подхода должны быть решены две проблемы: – корректное освобождение ресурсов, захваченных заблокированным потоком; – восстановление информации на момент, предшествующий тупику.
 Контрольные точки и транзакции • Для реализации этого подхода в программе устанавливаются такие точки, в которых запоминается состояние контекста потока. • Эти точки называются контрольными точками потока. • Изменение контекста потока между двумя контрольными точками называется транзакцией.
Контрольные точки и транзакции • Для реализации этого подхода в программе устанавливаются такие точки, в которых запоминается состояние контекста потока. • Эти точки называются контрольными точками потока. • Изменение контекста потока между двумя контрольными точками называется транзакцией.
 Откат. • Транзакция может быть зафиксирована или отменена. • Отмена транзакции называется откатом на контрольную точку. • После отката потоки разблокируются. • Если транзакция зафиксирована, то откат на контрольную точку невозможен.
Откат. • Транзакция может быть зафиксирована или отменена. • Отмена транзакции называется откатом на контрольную точку. • После отката потоки разблокируются. • Если транзакция зафиксирована, то откат на контрольную точку невозможен.
 Действия, выполняемые при откате • При откате выполняются следующие действия: – контекст потока восстанавливается в состояние, в котором он находился в контрольной точке; – восстанавливаются данные на момент прохождения контрольной точки; – освобождаются заблокированные ресурсы.
Действия, выполняемые при откате • При откате выполняются следующие действия: – контекст потока восстанавливается в состояние, в котором он находился в контрольной точке; – восстанавливаются данные на момент прохождения контрольной точки; – освобождаются заблокированные ресурсы.
 7. 7. Предотвращение тупиков
7. 7. Предотвращение тупиков
 Стратегии распределения ресурсов • Для того чтобы избежать возникновения тупиков, можно использовать следующие стратегии при распределении ресурсов: – Захват всех ресурсов; – Откат в случае отказа; – Упорядочивание запросов.
Стратегии распределения ресурсов • Для того чтобы избежать возникновения тупиков, можно использовать следующие стратегии при распределении ресурсов: – Захват всех ресурсов; – Откат в случае отказа; – Упорядочивание запросов.
 Захват всех ресурсов • Поток должен захватывать сразу все необходимые ему для работы ресурсы и только потом начинать свою работу. • Недостаток подхода: – неэффективное использование ресурсов компьютера, т. к. они блокируются для использования другими потоками.
Захват всех ресурсов • Поток должен захватывать сразу все необходимые ему для работы ресурсы и только потом начинать свою работу. • Недостаток подхода: – неэффективное использование ресурсов компьютера, т. к. они блокируются для использования другими потоками.
 Откат в случае отказа • Если в процессе работы потоку требуется дополнительный ресурс, но он получает отказ на захват этого ресурса, то поток должен освободить все принадлежащие ему ресурсы. • Недостаток подхода: – затраты на откат потока.
Откат в случае отказа • Если в процессе работы потоку требуется дополнительный ресурс, но он получает отказ на захват этого ресурса, то поток должен освободить все принадлежащие ему ресурсы. • Недостаток подхода: – затраты на откат потока.
 3. Упорядочивание запросов • Типы (классы) ресурсов линейно упорядочиваются (нумеруются). • В процессе своей работы поток может захватить только те ресурсы, тип которых больше типа уже используемых им ресурсов. • Недостаток подхода: – непригоден, если потребность в ресурсах определяется динамически.
3. Упорядочивание запросов • Типы (классы) ресурсов линейно упорядочиваются (нумеруются). • В процессе своей работы поток может захватить только те ресурсы, тип которых больше типа уже используемых им ресурсов. • Недостаток подхода: – непригоден, если потребность в ресурсах определяется динамически.
 7. 8. Алгоритм банкира для одного типа ресурсов • Алгоритм банкира – позволяет избежать тупик. • Этот алгоритм разработал Э. Дейкстра (1965). • Моделью алгоритма является работа банкира по обеспечению клиентов кредитами.
7. 8. Алгоритм банкира для одного типа ресурсов • Алгоритм банкира – позволяет избежать тупик. • Этот алгоритм разработал Э. Дейкстра (1965). • Моделью алгоритма является работа банкира по обеспечению клиентов кредитами.
 Формулировка задачи • Задача состоит в следующем: – банкир имеет ограниченное количество денег для выдачи кредитов; – требуется обеспечить клиентов кредитами: • кредит может выдаваться по частям; • каждый кредит не превышает ресурсов банкира; • сумма кредитов может превышать ресурсы банкира. • Аналогии в программных системах: – банкир – сервер; – клиент; – кредит – ресурс.
Формулировка задачи • Задача состоит в следующем: – банкир имеет ограниченное количество денег для выдачи кредитов; – требуется обеспечить клиентов кредитами: • кредит может выдаваться по частям; • каждый кредит не превышает ресурсов банкира; • сумма кредитов может превышать ресурсы банкира. • Аналогии в программных системах: – банкир – сервер; – клиент; – кредит – ресурс.
 Состояния системы • Для работы алгоритма определяются следующие состояния системы: – состояние считается безопасным, если система гарантирует невозможность возникновения тупика при распределении ресурсов; – иначе состояние называется небезопасным. • Алгоритм банкира рассматривает запросы на ресурсы и проверяет, к какому состоянию системы приведет выделение ресурса.
Состояния системы • Для работы алгоритма определяются следующие состояния системы: – состояние считается безопасным, если система гарантирует невозможность возникновения тупика при распределении ресурсов; – иначе состояние называется небезопасным. • Алгоритм банкира рассматривает запросы на ресурсы и проверяет, к какому состоянию системы приведет выделение ресурса.
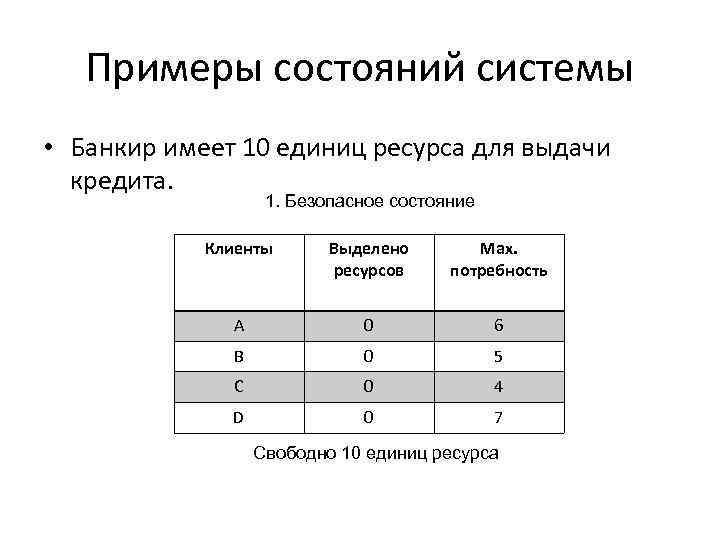 Примеры состояний системы • Банкир имеет 10 единиц ресурса для выдачи кредита. 1. Безопасное состояние Клиенты Выделено ресурсов Мах. потребность A 0 6 B 0 5 C 0 4 D 0 7 Свободно 10 единиц ресурса
Примеры состояний системы • Банкир имеет 10 единиц ресурса для выдачи кредита. 1. Безопасное состояние Клиенты Выделено ресурсов Мах. потребность A 0 6 B 0 5 C 0 4 D 0 7 Свободно 10 единиц ресурса
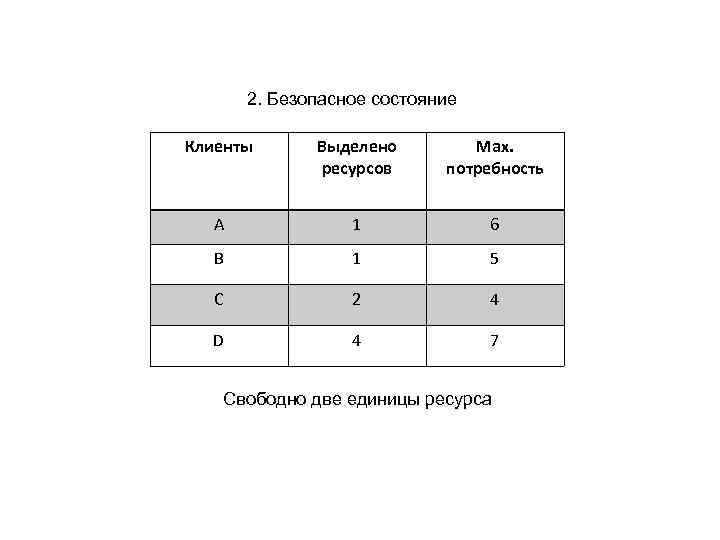 2. Безопасное состояние Клиенты Выделено ресурсов Мах. потребность A 1 6 B 1 5 C 2 4 D 4 7 Свободно две единицы ресурса
2. Безопасное состояние Клиенты Выделено ресурсов Мах. потребность A 1 6 B 1 5 C 2 4 D 4 7 Свободно две единицы ресурса
 3. Небезопасное состояние Клиенты Выделено ресурсов Мах. потребность A 1 6 B 2 5 C 2 4 D 4 7 Свободна единица ресурса
3. Небезопасное состояние Клиенты Выделено ресурсов Мах. потребность A 1 6 B 2 5 C 2 4 D 4 7 Свободна единица ресурса
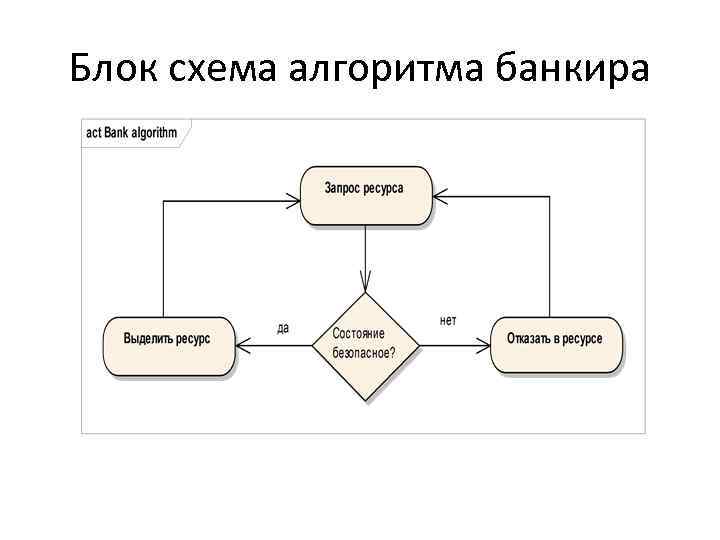 Блок схема алгоритма банкира
Блок схема алгоритма банкира
 Задача № 1 • Процесс включает пять потоков: Ti, 1 <= i <= 5, • которые используют девять повторно используемых ресурсов: Rj, 1 <= j <= 9.
Задача № 1 • Процесс включает пять потоков: Ti, 1 <= i <= 5, • которые используют девять повторно используемых ресурсов: Rj, 1 <= j <= 9.
 • Потоки процесса выполнили следующие запросы на распределение ресурсов: – поток T 1: • захватил ресурс R 1; • ждет ресурсы R 7, R 9; – поток T 2: • захватил ресурсы R 2, R 6; • ждет ресурс R 8; – поток T 3: • захватил ресурс R 3;
• Потоки процесса выполнили следующие запросы на распределение ресурсов: – поток T 1: • захватил ресурс R 1; • ждет ресурсы R 7, R 9; – поток T 2: • захватил ресурсы R 2, R 6; • ждет ресурс R 8; – поток T 3: • захватил ресурс R 3;
 – поток T 4: • захватил ресурсы R 7, R 8; • ждет ресурс R 5; – поток T 5: • захватил ресурсы R 5, R 9; • ждет ресурс R 6. • Требуется определить, находится ли процесс в тупике.
– поток T 4: • захватил ресурсы R 7, R 8; • ждет ресурс R 5; – поток T 5: • захватил ресурсы R 5, R 9; • ждет ресурс R 6. • Требуется определить, находится ли процесс в тупике.
 Решение • 1. Определяем потоки, которые находятся в состоянии ожидания: T 1, T 2, T 4, T 5. • Строим граф распределения ресурсов для этих потоков.
Решение • 1. Определяем потоки, которые находятся в состоянии ожидания: T 1, T 2, T 4, T 5. • Строим граф распределения ресурсов для этих потоков.

 • 3. Так как граф распределения ресурсов содержит цикл: (T 2, T 4), (T 4, T 5), (T 5, T 2), то процесс находится в тупике.
• 3. Так как граф распределения ресурсов содержит цикл: (T 2, T 4), (T 4, T 5), (T 5, T 2), то процесс находится в тупике.
 Задача № 2 • В системе работают n процессов, которые используют m ресурсов типа R. Пусть каждому процессу выделено Pi ресурсов и для каждого процесса известно Mi – максимальное количество ресурсов, которые он может использовать, 1 <= i <= n.
Задача № 2 • В системе работают n процессов, которые используют m ресурсов типа R. Пусть каждому процессу выделено Pi ресурсов и для каждого процесса известно Mi – максимальное количество ресурсов, которые он может использовать, 1 <= i <= n.
 • Вопрос 1. Используя алгоритм банкира, требуется определить, сколько ресурсов дополнительно можно выделить процессу j, где • n = 5, • m = 20, • j = 3, • Mi = (5, 10, 3), • Pi = (4, 7, 1, 5, 0).
• Вопрос 1. Используя алгоритм банкира, требуется определить, сколько ресурсов дополнительно можно выделить процессу j, где • n = 5, • m = 20, • j = 3, • Mi = (5, 10, 3), • Pi = (4, 7, 1, 5, 0).
 Решение. Применяем алгоритм банкира. • 1. Определяем, количество распределенных и свободных ресурсов. – Распределено = 4 + 7 + 1 + 5 + 0 = 17 – Свободно = 20 – 17 = 3 • 2. Строим вектор количества ресурсов, которые могут запросить процессы: – (1, 3, 4, 5, 3) • 3. Для перехода системы в безопасное состояние, требуется, чтобы оставался 1 свободный ресурс R для процесса P 1. • Следовательно, процессу 3 можно дополнительно выделить 3 – 1 = 2 единицы ресурса R.
Решение. Применяем алгоритм банкира. • 1. Определяем, количество распределенных и свободных ресурсов. – Распределено = 4 + 7 + 1 + 5 + 0 = 17 – Свободно = 20 – 17 = 3 • 2. Строим вектор количества ресурсов, которые могут запросить процессы: – (1, 3, 4, 5, 3) • 3. Для перехода системы в безопасное состояние, требуется, чтобы оставался 1 свободный ресурс R для процесса P 1. • Следовательно, процессу 3 можно дополнительно выделить 3 – 1 = 2 единицы ресурса R.
 • Вопрос 2. Процесс 3 запросил у системы 3 единицы ресурса R. Удовлетворит ли система этот запрос. • Решение. Так как система может выделить процессу 3 максимум 2 единицы ресурса, то процесс 3 получит отказ в выделении ресурсов.
• Вопрос 2. Процесс 3 запросил у системы 3 единицы ресурса R. Удовлетворит ли система этот запрос. • Решение. Так как система может выделить процессу 3 максимум 2 единицы ресурса, то процесс 3 получит отказ в выделении ресурсов.


