7 2 Day 2 Rules for Means and

7. 2 Day 2: Rules for Means and Variances

3/4 CW Probability WARM UP 2/3 1/2 1/3 R R NE A travel agent books passages on three different tours, 1/2 1/6 R with half of her customers choosing Caribbean Waters EV (CW), one-third choosing New England’s Historic Trail (NE), the rest choosing European Vacation (EV). The agent has noted that three-quarters of those who take CW return to book passage again, two-thirds of those who take NE return and one-half of those who take EV return. If a customer does return, what is the probability that the person went on NE?

Rules for Means Rule 1: If X is a random variable and a and b are fixed numbers, then μa + b. X = a + bμX Rule 2: If X and Y are random variables, then μX + Y = μX + μY

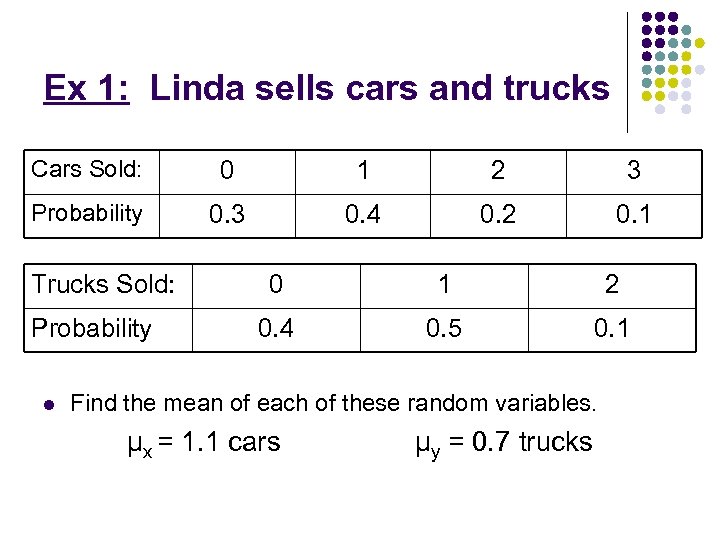Ex 1: Linda sells cars and trucks Cars Sold: 0 1 2 3 Probability 0. 3 0. 4 0. 2 0. 1 Trucks Sold: Probability l 0 1 2 0. 4 0. 5 0. 1 Find the mean of each of these random variables. μx = 1. 1 cars μy = 0. 7 trucks

l At her commision rate of 25%, Linda expects to earn $350 for each car sold and $400 for each truck sold. So her earnings are Z = 350 X + 400 Y l Combining rules 1 and 2, her mean earnings are μz = 350μx + 400μy = (350)(1. 1) + (400)(0. 7) = $650

Rules for Variances Adding a constant a to a random variable changes its mean but does not change its variability. Rule 1: If X is a random variable and a and b are fixed numbers, then σ2 a + b. X = b 2σx 2 Rule 2: If X and Y are independent random variables, then σ2 X+Y = σx 2 + σY 2 σ2 X – Y = σx 2 + σY 2 This is the addition rule for variances of independent random variables.

Rules for Standard Deviations l l Standard deviations are most easily combined by using the rules for variances rather than by giving separate rules for standard deviations. Note that variances of independent variables add, standard deviations do not generally add!

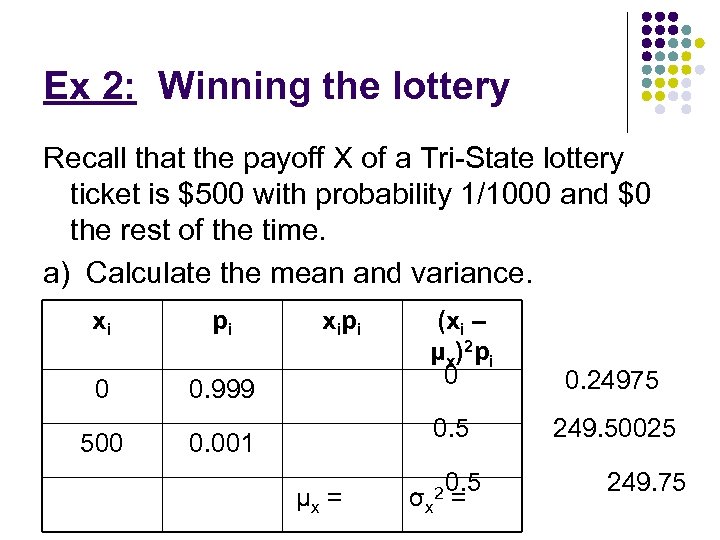Ex 2: Winning the lottery Recall that the payoff X of a Tri-State lottery ticket is $500 with probability 1/1000 and $0 the rest of the time. a) Calculate the mean and variance. xi pi 0 0. 999 500 xi p i (xi – μ x )2 p i 0 0. 5 0. 001 μx = 2 0. 5 σx = 0. 24975 249. 50025 249. 75

Games of chance typically have large standard deviations. Large variability makes gambling more exciting! b) Find the standard deviation. σx = $15. 80 Basically, you lose an average of 50 cents on a ticket. c) If it cost $1 to buy a ticket, what is the mean amount that you win? μw = μx – 1 = -$0. 50 Note that the variance and standard deviation stay the same by Rule 1 for Variances.

d) Suppose that you buy two tickets on two different days. These tickets are independent due to the fact that drawings are held each day. l l l Find the mean total payoff X + Y. Note that this is not the μX + Y = μX + μY = $0. 50 + $0. 50 the $1. 00 = individual sum of standard deviations Find the variance of X + Y. ($15. 80 + $15. 80) σ2 X + Y = σX 2 + σY 2 = 249. 75 + 249. 75 = 499. 50 Find the standard deviation of the total payoff. σX + Y =

Ex 3: SAT Scores l Below are the means and standard deviations of SAT scores at a certain college. SAT Math Score X SAT Verbal Score Y l It wouldn’t make sense to add the standard deviations, due to the fact that the test scores are not independent. μx = 519 σx = 115 μY = 507 σY = 111 Find the mean overall SAT Score. μX + Y = μX + μY = 519 + 507 = 1026