 7. 11. (ПРОДОЛЖЕНИЕ Примера 7. 1. ) 1
7. 11. (ПРОДОЛЖЕНИЕ Примера 7. 1. ) 1
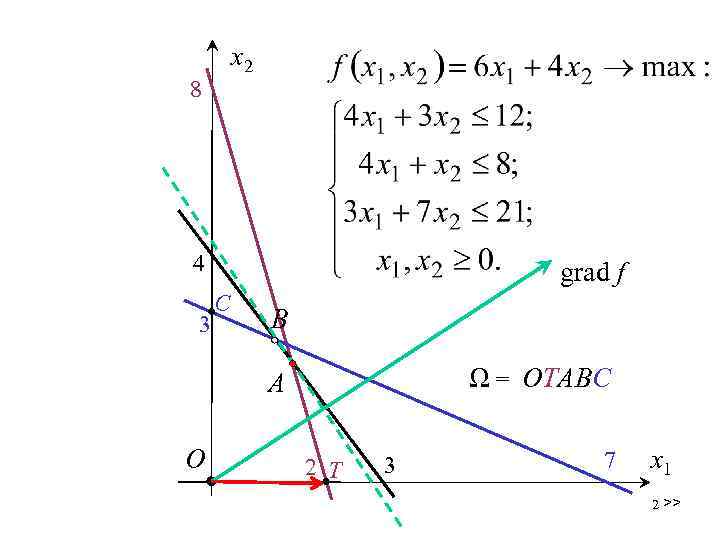 x 2 8 4 3 grad f С B Ω = OТАВС A О 2 Т 3 7 x 1 2 >>
x 2 8 4 3 grad f С B Ω = OТАВС A О 2 Т 3 7 x 1 2 >>
 7. 11. (ПРОДОЛЖЕНИЕ Примера 7. 1. ) Из вершины (0; 0; 12; 8; 21) – в вершину (2; 0; 4; 0; 15): св. баз. При этом согласно соответствию переменных преобразуется двойственная задача: св. баз. 3 >>
7. 11. (ПРОДОЛЖЕНИЕ Примера 7. 1. ) Из вершины (0; 0; 12; 8; 21) – в вершину (2; 0; 4; 0; 15): св. баз. При этом согласно соответствию переменных преобразуется двойственная задача: св. баз. 3 >>
 4 >>
4 >>
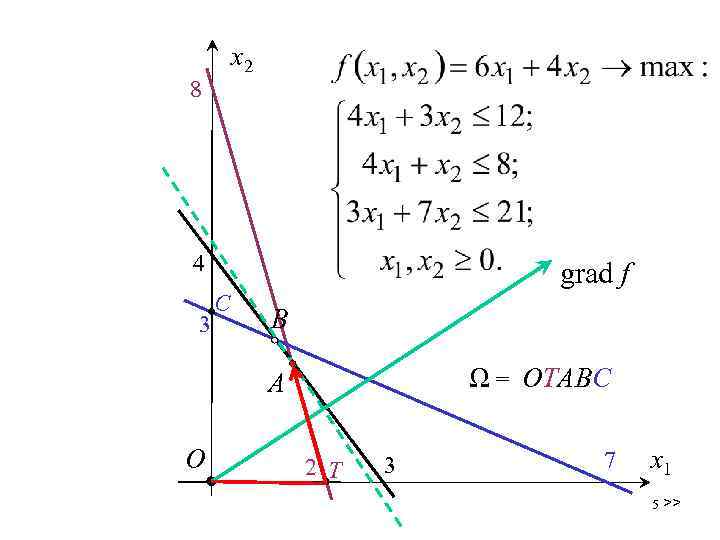 x 2 8 4 3 grad f С B Ω = OТАВС A О 2 Т 3 7 x 1 5 >>
x 2 8 4 3 grad f С B Ω = OТАВС A О 2 Т 3 7 x 1 5 >>
 Из вершины (2; 0; 4; 0; 15) – в вершину (1. 5; 2; 0; 0; 2. 5) = х*: св. баз. В двойственной задаче: св. баз. 6 >>
Из вершины (2; 0; 4; 0; 15) – в вершину (1. 5; 2; 0; 0; 2. 5) = х*: св. баз. В двойственной задаче: св. баз. 6 >>
 Итог в матричной форме: 7 >>
Итог в матричной форме: 7 >>
 Итог в матричной форме: – оптимальные значения переменных двойственной задачи (оценки ресурсов) оказались коэффициентами ЦФ основой задачи. 8 >>
Итог в матричной форме: – оптимальные значения переменных двойственной задачи (оценки ресурсов) оказались коэффициентами ЦФ основой задачи. 8 >>
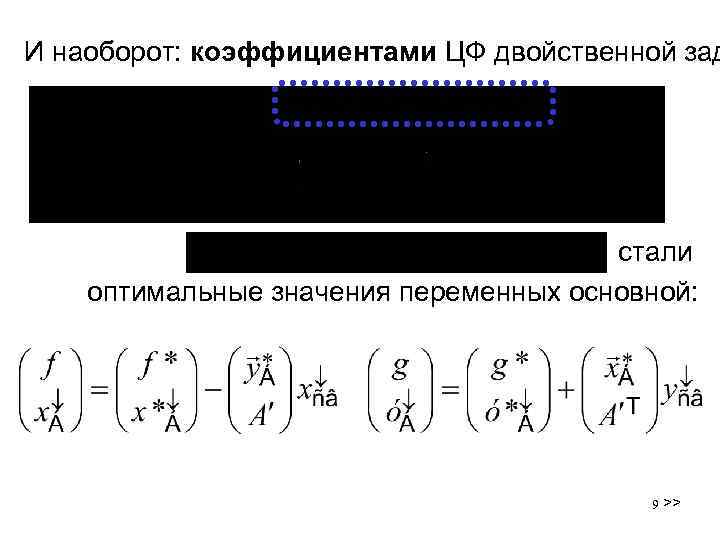 И наоборот: коэффициентами ЦФ двойственной зад стали оптимальные значения переменных основной: 9 >>
И наоборот: коэффициентами ЦФ двойственной зад стали оптимальные значения переменных основной: 9 >>
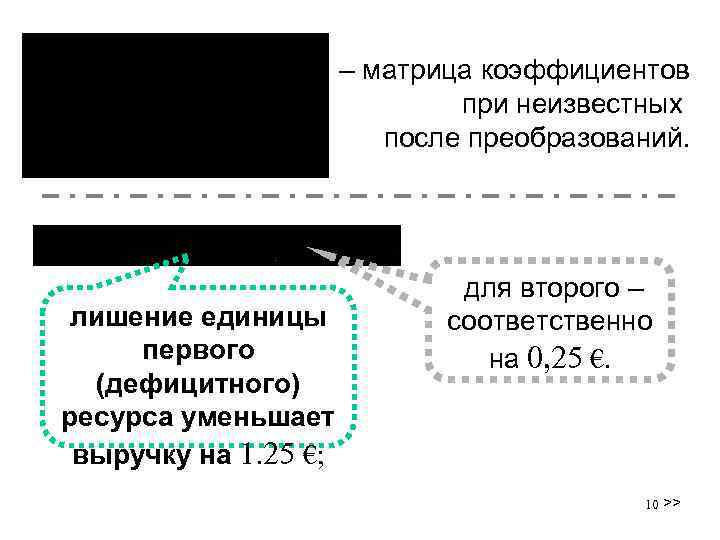 – матрица коэффициентов при неизвестных после преобразований. лишение единицы первого (дефицитного) ресурса уменьшает выручку на 1. 25 €; для второго – соответственно на 0, 25 €. 10 >>
– матрица коэффициентов при неизвестных после преобразований. лишение единицы первого (дефицитного) ресурса уменьшает выручку на 1. 25 €; для второго – соответственно на 0, 25 €. 10 >>
 Добавим к i-му ресурсу εi единиц – соответственно уменьшим балансовые переменные: Оптимальная выручка может увеличиться на 11 >>
Добавим к i-му ресурсу εi единиц – соответственно уменьшим балансовые переменные: Оптимальная выручка может увеличиться на 11 >>
 структура оптимального плана останется прежней нулевым значениям свободных переменных по-прежнему соответствуют неотрицательные значения базисных: 12 >>
структура оптимального плана останется прежней нулевым значениям свободных переменных по-прежнему соответствуют неотрицательные значения базисных: 12 >>
 Проследим за изменением цен изделий: 13 >>
Проследим за изменением цен изделий: 13 >>
 – оптимальный план остался прежним 14
– оптимальный план остался прежним 14
 – оптимальный план остался прежним выручка увеличится на 1. 5 a + 2 b. 15 >>
– оптимальный план остался прежним выручка увеличится на 1. 5 a + 2 b. 15 >>
 7. 12. Пример анализа решения ЗЛП
7. 12. Пример анализа решения ЗЛП
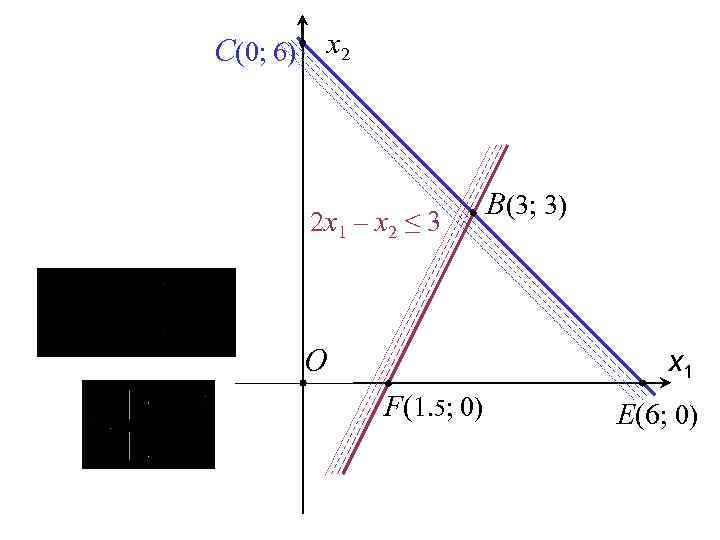 C(0; 6) x 2 2 x 1 – x 2 ≤ 3 O B(3; 3) x 1 F(1. 5; 0) Е(6; 0)
C(0; 6) x 2 2 x 1 – x 2 ≤ 3 O B(3; 3) x 1 F(1. 5; 0) Е(6; 0)
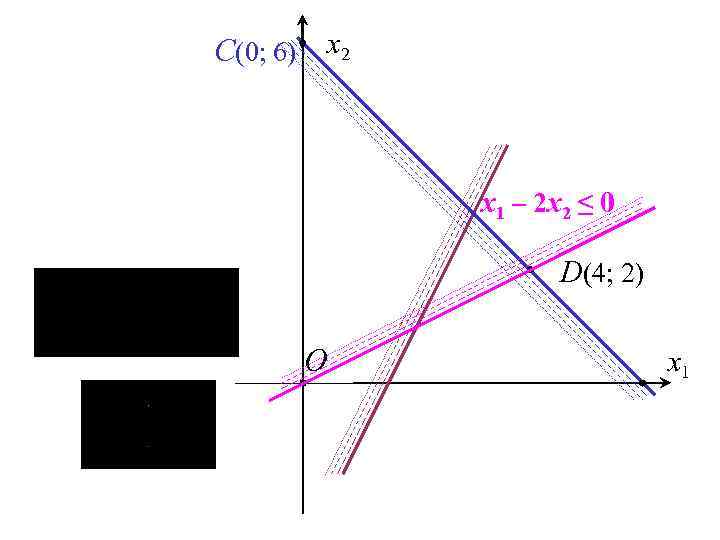 C(0; 6) x 2 x 1 – 2 x 2 ≤ 0 D(4; 2) O x 1
C(0; 6) x 2 x 1 – 2 x 2 ≤ 0 D(4; 2) O x 1
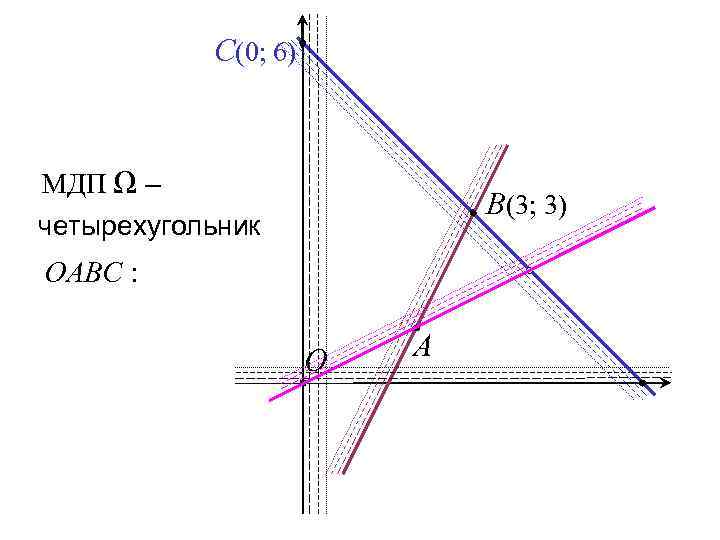 C(0; 6) МДП Ω – B(3; 3) четырехугольник OABC : O A
C(0; 6) МДП Ω – B(3; 3) четырехугольник OABC : O A
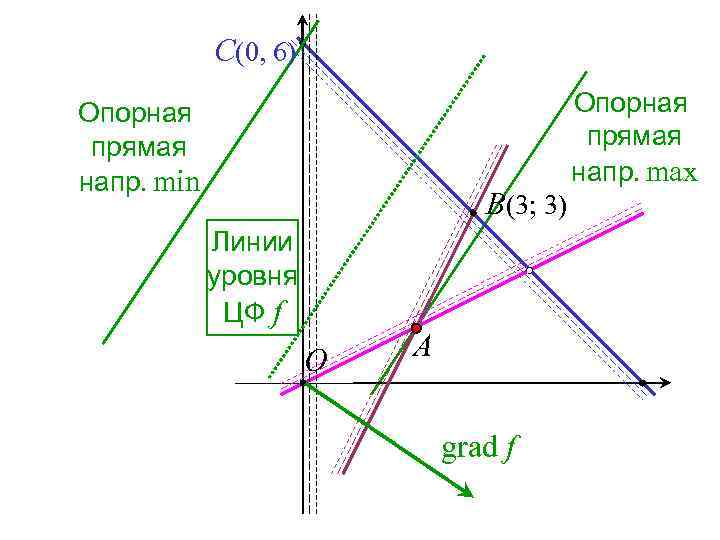 C(0, 6) Опорная прямая напр. min B(3; 3) Линии уровня ЦФ f O A grad f Опорная прямая напр. max
C(0, 6) Опорная прямая напр. min B(3; 3) Линии уровня ЦФ f O A grad f Опорная прямая напр. max
 На МДП Ω целевая функция f достигает наибольшего значения в точке А(2; 1) −
На МДП Ω целевая функция f достигает наибольшего значения в точке А(2; 1) −
 Из отчета по устойчивост Изменяемая ячейка – переменная x 1: Нормированная (приведенная) стоимость: 0 x 1 – базисная переменная (свободные переменные – балансовые) Целевой коэффициент: с1 = 3
Из отчета по устойчивост Изменяемая ячейка – переменная x 1: Нормированная (приведенная) стоимость: 0 x 1 – базисная переменная (свободные переменные – балансовые) Целевой коэффициент: с1 = 3
 Можно ли изменить с1 при условии, что A(2; 1) остается оптимальной вершиной? Допустимое увеличение: α = 1 Допустимое уменьшение: β = 2 Если с1 [3 – β; 3 + α] = [1; 4], а с2 не изменяется, то вершина А(2; 1) оптимальна.
Можно ли изменить с1 при условии, что A(2; 1) остается оптимальной вершиной? Допустимое увеличение: α = 1 Допустимое уменьшение: β = 2 Если с1 [3 – β; 3 + α] = [1; 4], а с2 не изменяется, то вершина А(2; 1) оптимальна.
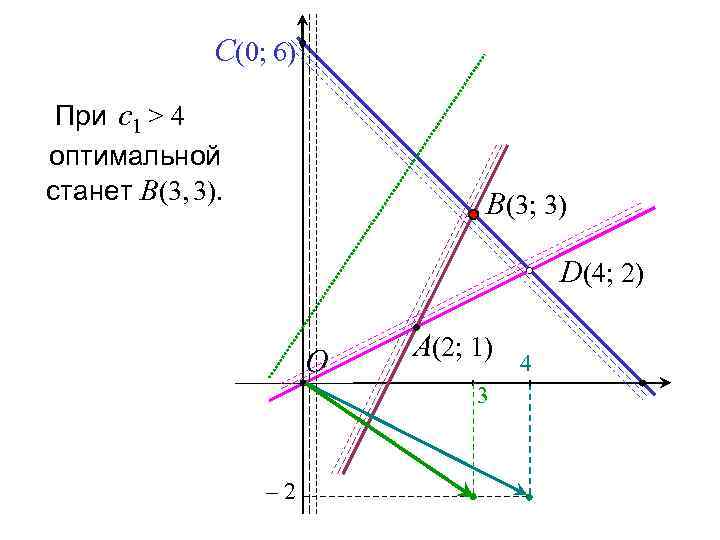 C(0; 6) При с1 > 4 оптимальной станет В(3, 3). B(3; 3) D(4; 2) O A(2; 1) 3 – 2 4
C(0; 6) При с1 > 4 оптимальной станет В(3, 3). B(3; 3) D(4; 2) O A(2; 1) 3 – 2 4
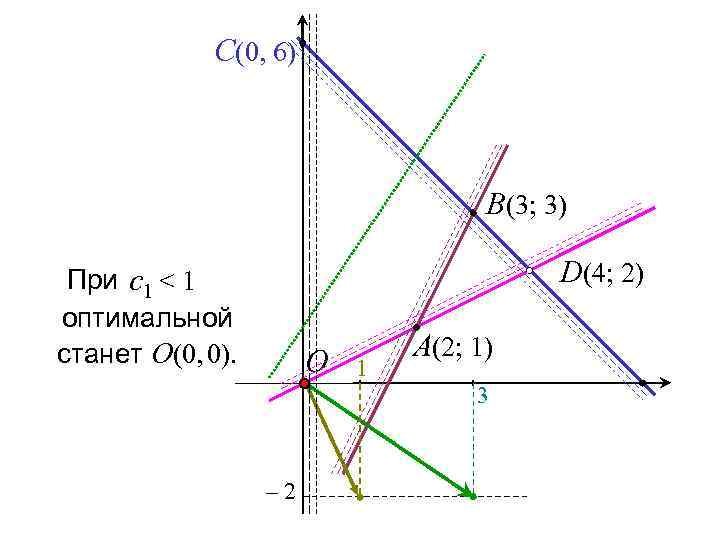 C(0, 6) B(3; 3) D(4; 2) При с1 < 1 оптимальной станет О(0, 0). O 1 A(2; 1) 3 – 2
C(0, 6) B(3; 3) D(4; 2) При с1 < 1 оптимальной станет О(0, 0). O 1 A(2; 1) 3 – 2
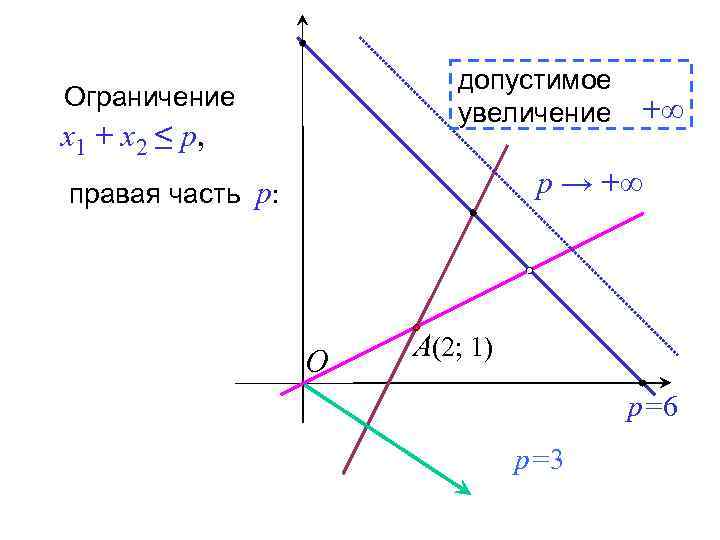 допустимое увеличение Ограничение x 1 + x 2 ≤ p, +∞ p → +∞ правая часть p: O A(2; 1) p=6 p=3
допустимое увеличение Ограничение x 1 + x 2 ≤ p, +∞ p → +∞ правая часть p: O A(2; 1) p=6 p=3
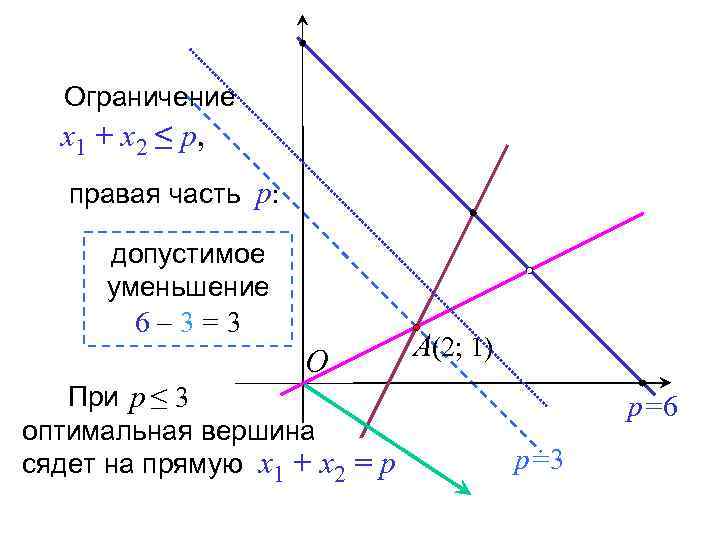 Ограничение x 1 + x 2 ≤ p, правая часть p: допустимое уменьшение 6– 3=3 O При p ≤ 3 оптимальная вершина сядет на прямую x 1 + x 2 = p A(2; 1) p=6 p=3
Ограничение x 1 + x 2 ≤ p, правая часть p: допустимое уменьшение 6– 3=3 O При p ≤ 3 оптимальная вершина сядет на прямую x 1 + x 2 = p A(2; 1) p=6 p=3
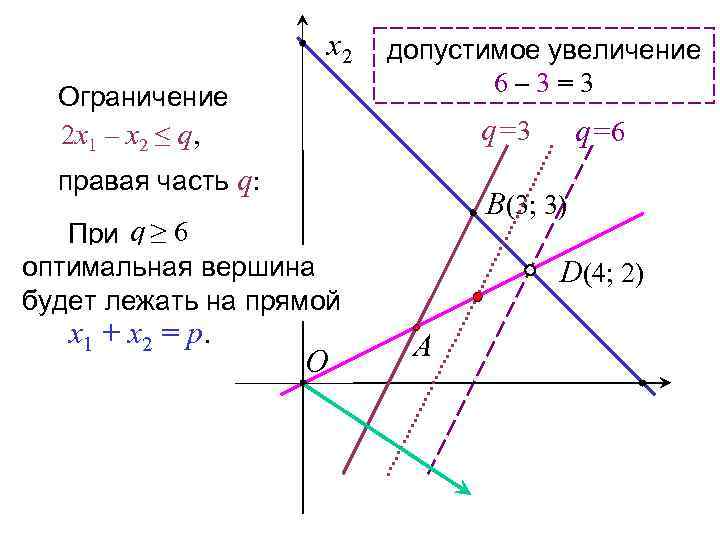 x 2 Ограничение 2 x 1 – x 2 ≤ q, допустимое увеличение 6– 3=3 q=3 правая часть q: B(3; 3) При q ≥ 6 оптимальная вершина будет лежать на прямой x 1 + x 2 = p. O q=6 D(4; 2) A
x 2 Ограничение 2 x 1 – x 2 ≤ q, допустимое увеличение 6– 3=3 q=3 правая часть q: B(3; 3) При q ≥ 6 оптимальная вершина будет лежать на прямой x 1 + x 2 = p. O q=6 D(4; 2) A
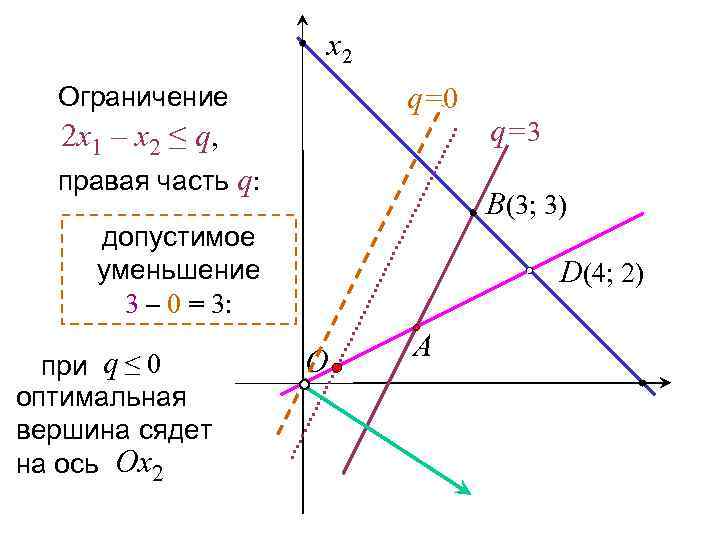 x 2 q=0 Ограничение 2 x 1 – x 2 ≤ q, правая часть q: B(3; 3) допустимое уменьшение 3 – 0 = 3: при q ≤ 0 оптимальная вершина сядет на ось Оx 2 q=3 D(4; 2) O A
x 2 q=0 Ограничение 2 x 1 – x 2 ≤ q, правая часть q: B(3; 3) допустимое уменьшение 3 – 0 = 3: при q ≤ 0 оптимальная вершина сядет на ось Оx 2 q=3 D(4; 2) O A
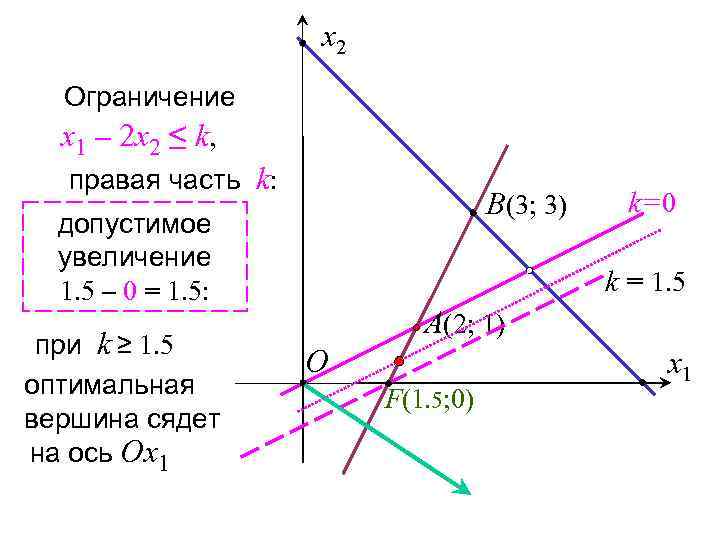 x 2 Ограничение x 1 – 2 x 2 ≤ k, правая часть k: B(3; 3) допустимое увеличение 1. 5 – 0 = 1. 5: при k ≥ 1. 5 оптимальная вершина сядет на ось Оx 1 k=0 k = 1. 5 A(2; 1) O F(1. 5; 0) x 1
x 2 Ограничение x 1 – 2 x 2 ≤ k, правая часть k: B(3; 3) допустимое увеличение 1. 5 – 0 = 1. 5: при k ≥ 1. 5 оптимальная вершина сядет на ось Оx 1 k=0 k = 1. 5 A(2; 1) O F(1. 5; 0) x 1
 x 2 допустимое уменьшение 0 – (– 3) = 3 Ограничение k = – 3 x 1 – 2 x 2 ≤ k, правая часть k: при k ≤ – 3 оптимальная вершина окажется на прямой x 1 + x 2 = p. B(3; 3) k=0 A(2; 1) O F(1. 5; 0) x 1
x 2 допустимое уменьшение 0 – (– 3) = 3 Ограничение k = – 3 x 1 – 2 x 2 ≤ k, правая часть k: при k ≤ – 3 оптимальная вершина окажется на прямой x 1 + x 2 = p. B(3; 3) k=0 A(2; 1) O F(1. 5; 0) x 1
 Из отчета по пределам В каких пределах могут меняться значения переменных при условии А(x 1; x 2) Ω ? Изменяемое имя x 1 Значение 2 Нижний предел 0 Целевой результат – 2 Значение 2 Верхний предел 2 Целевой результат 4
Из отчета по пределам В каких пределах могут меняться значения переменных при условии А(x 1; x 2) Ω ? Изменяемое имя x 1 Значение 2 Нижний предел 0 Целевой результат – 2 Значение 2 Верхний предел 2 Целевой результат 4
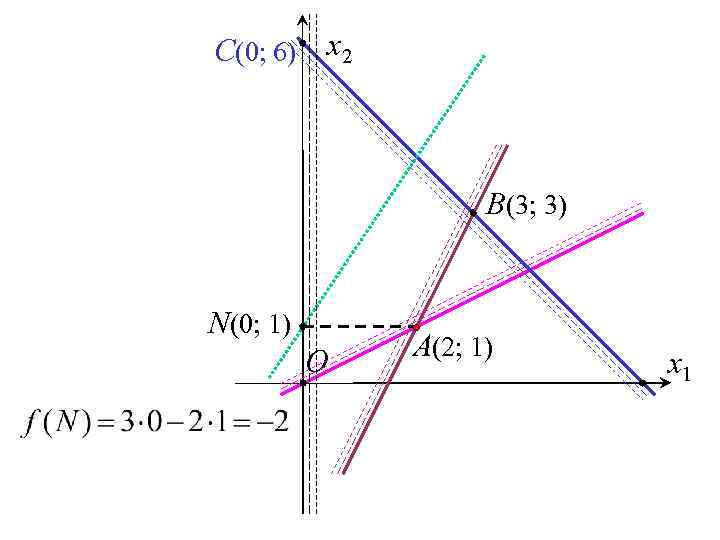 C(0; 6) x 2 B(3; 3) N(0; 1) O A(2; 1) x 1
C(0; 6) x 2 B(3; 3) N(0; 1) O A(2; 1) x 1
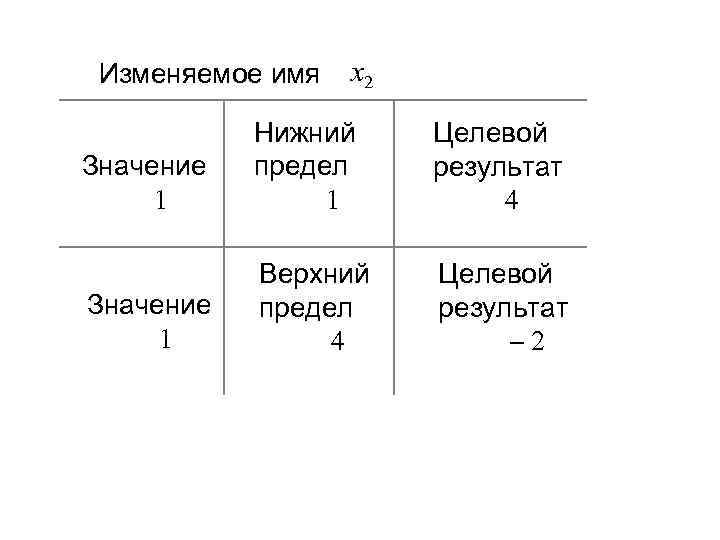 Изменяемое имя x 2 Значение 1 Нижний предел 1 Целевой результат 4 Значение 1 Верхний предел 4 Целевой результат – 2
Изменяемое имя x 2 Значение 1 Нижний предел 1 Целевой результат 4 Значение 1 Верхний предел 4 Целевой результат – 2
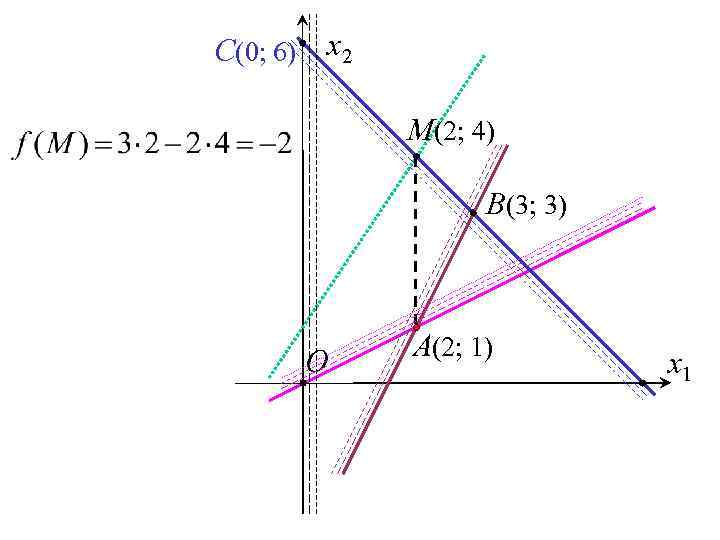 C(0; 6) x 2 M(2; 4) B(3; 3) O A(2; 1) x 1
C(0; 6) x 2 M(2; 4) B(3; 3) O A(2; 1) x 1


