6 Расчет замкнутых местных сетей 6 1 Основные

6. Расчет замкнутых местных сетей 6. 1. Основные определения и область применения Существенным недостатком рассмотренных в предыдущих главах разомкнутых (радиальных) сетей является то, что в случае выхода из работы какого-либо участка этих сетей значительная часть потребителей лишается электроснабжения. Поэтому для обеспечения надежного электроснабжения ответственных потребителей, не терпящих длительных перерывов в электроснабжении, применяют замкнутые сети.

• Замкнутыми сетями называются сети, в которых электроэнергия к потребителям подается не менее чем с двух сторон. Различают простые замкнутые сети, в которых присоединенные к ним нагрузки питаются не более чем с двух сторон, и сложные замкнутые сети, к узловым точкам которых электроэнергия может подаваться не менее чем с трех сторон.

Простая замкнутая сеть может иметь либо один источник питания, и тогда она выполняется в виде замкнутого кольца и называется кольцевой сетью, либо два источника питания, питающих линию с двух сторон, и тогда она называется сетью с двусторонним питанием.

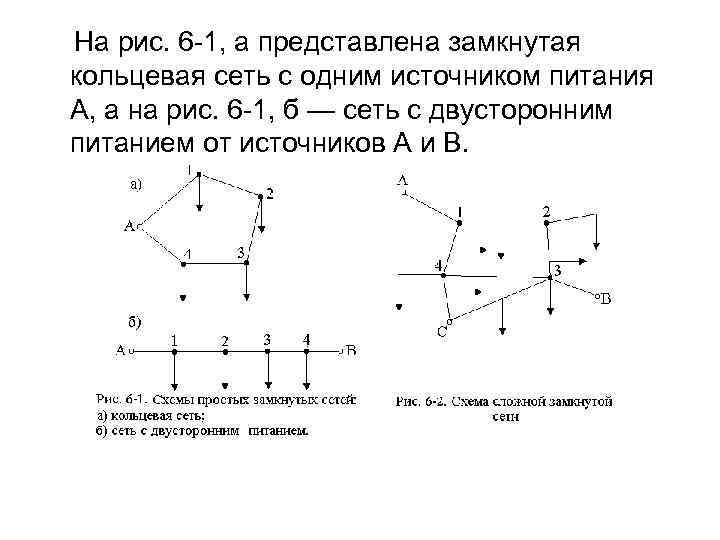На рис. 6 -1, а представлена замкнутая кольцевая сеть с одним источником питания A, а на рис. 6 -1, б — сеть с двусторонним питанием от источников А и В.

• Легко видеть, что кольцевую сеть можно превратить в сеть с двусторонним питанием, разрезав ее по источникам питания. Пример сложной замкнутой сети с тремя источниками питания А, В и С и четырьмя узловыми точками 1, 2, 3 и 4 изображен на рис. 6 -2. Такая сеть не может быть превращена указанным выше способом в сеть с двусторонним питанием и требует сложных преобразований (см. 10. 5. ).

• В местных сетях применяют преимущественно простые замкнутые сети — кольцевые или двустороннего питания, а также двухцепные линии, по существу являющиеся частным случаем кольцевого питания.

• Область применения сложных замкнутых схем в местных сетях ограничена так называемой “замкнутой сеткой” низкого напряжения. Этот вид сетей применяют в крупных городах для питания городской коммунальной нагрузки на напряжении 400/230 В. Схема такой сети представляет собой линии, расположенные по улицам города, смыкающиеся на перекрестках и питающиеся параллельно от нескольких источников (рис. 6 -3).

• В практических расчетах замкнутую сетку условно разрезают в точках, равноудаленных от точек питания (см. пунктирные линии на рис. 6 -3 ), превращая ее таким образом в разомкнутую сеть, которую рассчитывают обычными методами, например методом минимума расхода металла и допустимой потери напряжения.

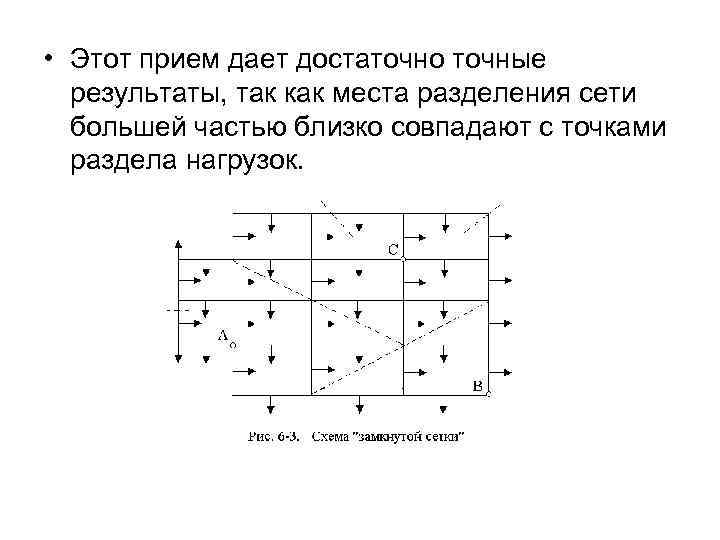• Этот прием дает достаточно точные результаты, так как места разделения сети большей частью близко совпадают с точками раздела нагрузок.

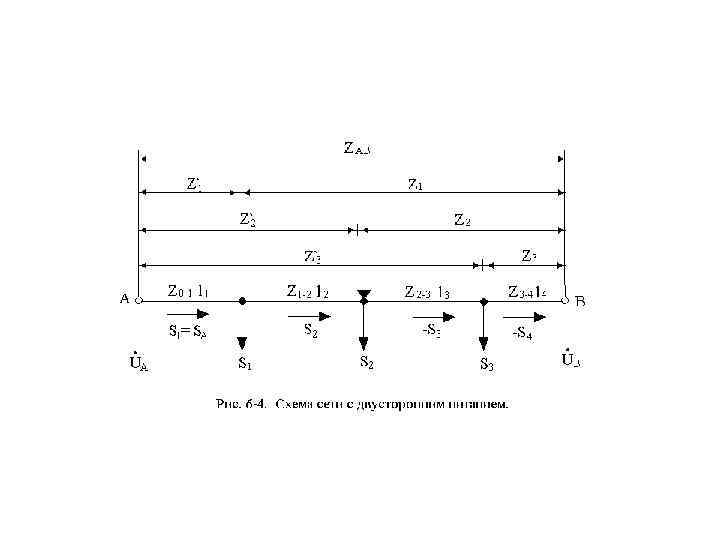
6. 2. Расчет линий с двусторонним питанием • Рассмотрим методику расчета линий с двусторонним питанием, являющуюся общим случаем расчета простых замкнутых сетей, поскольку, как указывалось в 6 -1, кольцевая сеть легко приводится к схеме двустороннего питания. Схема такой сети для трех нагрузок изображена на рис. 6 -4. Здесь s 1; s 2 и s 3 — нагрузки в точках 1, 2 и 3; S 1, S 2, S 3 и S 4 — полные мощности на участках линии; Z 0 -1, Z 1 -2, Z 2 -3 и Z 3 -4; l 1, l 2, l 3 и l 4 — соответственно полные сопротивления и длины участков; A и В — источники питания; UA и UB — напряжения источников питания.

Падение линейного напряжения на любом участке линии между нагрузками будет равно: где Ii — ток на данном участке; Zi — сопротивление этого участка. Поскольку То где Ui — сопряженный вектор напряжения в данной точке сети.

• Полагая вектор Ui ориентированным по вещественной оси, получим: где Si и Ui взяты для одной и той же точки участка.

• Вектор напряжения Ui изменяется вдоль линии по мере удаления от источника питания. Однако, пренебрегая потерями мощности в линии, т. е. исходя из постоянства напряжения вдоль каждого участка и полагая U 1 = U 2 =. . . = Un (что для сетей местного значения вполне допустимо), можем на основании второго закона Кирхгофа написать следующее равенство для падений напряжения между точками А и В: • Или • где Uн — номинальное напряжение сети.

• Одновременно, пользуясь первым законом Кирхгофа для точек 1, 2, 3 и исходя из принятого допущения об отсутствии потерь мощности в сети, можно составить следующие равенства: Подставив эти выражения в уравнение (6 -1), получим: Или Отсюда искомая мощность, выходящая в линию из пункта А, будет равна:

Обозначив сопротивления от пункта В до нагрузок 1, 2, 3 соответственно через Z 1, Z 2 и Z 3, а полное сопротивление линии между пунктами A и В через ZAB и подставив эти величины в формулу (6 -3), получим: или в общем виде для многих нагрузок: Аналогичную формулу можно вывести и для нагрузки, идущей из пункта В: где Z'i — сопротивления от пункта А до каждой нагрузки.

• Остальные нагрузки по участкам, зная Z', легко найти, пользуясь выражениями (6 -2), а так как на схеме рис. 6 -4 за положительное направление мощностей было условно принято направление от А к В, то часть нагрузок па участках, прилегающих к источнику питания В, получится с отрицательным знаком, что будет указывать на их обратное направление. В некоторой точке окажется, что мощности к ней притекают с двух сторон. В данном случае такой точкой является точка 2. Эта точка называется точкой раздела и обычно обозначается значком q.

• Второй член в выражении (6 -4) представляет собой уравнительную мощность, протекающую по линии АВ вследствие разности напряжений между этими пунктами. Эта мощность не зависит от нагрузок линии, так как она будет иметь место и при s 1, s 2, … , sn = 0.

• При равенстве напряжений в точках питания или при кольцевой схеме (когда точки А и В совмещены) UА — UB. Второй член в правой части равенства (6 -4) пропадает, и формула для определения мощности, выходящей из пункта A, принимает вид: • При расчете местных сетей обычно пользуются формулой (6 -5), считая напряжения источников одинаковыми.

• Таким образом, для того чтобы определить мощность, выходящую из одного из питательных пунктов, необходимо определить сумму моментов нагрузок относительно другого питательного пункта и разделить ее на полное сопротивление всего участка сети с двусторонним питанием.

• При одинаковых напряжениях на питательных пунктах или при расчете кольцевых схем падение напряжения от питательных пунктов до точки раздела одинаково с обеих сторон. Поэтому в этой точке сеть может быть условно разрезана и потери напряжения определены для любой из половин как для сети с односторонним питанием.

Чтобы определить с помощью полученных выше формул, как распределяются мощности в линиях с двусторонним питанием, в общем случае подсчет производят в комплексной форме:

• В некоторых случаях расчеты можно упростить, перейдя к раздельному определению распределения активной и реактивной мощностей и заменив в формуле (6 -5) сопротивление ZAВ соответствующей проводимостью: • Где

Подставив эти величины в формулу (6 -5), получим: Или Произведя все действия и разделив вещественные и мнимые члены, получим:

• Формулы (6 -6) позволяют вести подсчет в отдельности для активной и реактивной нагрузок, пользуясь абсолютными значениями вещественных и мнимых составляющих нагрузок и сопротивлений. Эти формулы можно использовать для расчета потокораспределения в сетях двустороннего питания и с разными уровнями напряжения источников питания. Однако в этом случае на полученный по формулам (6 -6) результат потокораспределения необходимо наложить уравнительную мощность, рассчитанную по второму члену выражения (6 -4).

• В случае, если напряжения источников питания совпадают по фазе, уравнительная мощность, протекающая от одного источника питания к другому, будет равна:

• Необходимость в подобных расчетах возникает тогда, когда в целях перераспределения реактивной мощности для оптимального использования линий замкнутой сети на одном из питающих пунктов устанавливают вольтодобавочные автотрансформаторы.

• Определив, как в линии двустороннего питания распределяются нагрузки, переходят к подсчету потерь напряжения обычным способом.

6. 3. Частные случаи расчета сетей с двусторонним питанием • В некоторых частных случаях выведенные выше формулы расчета сетей с двусторонним питанием могут быть значительно упрощены. Рассмотрим эти случаи. Однородная линия Если на всей длине линии провода расположены на опорах одинаково и имеют теоретически постоянное соотношение реактивного и активного сопротивлений, т. е.

• то формулу (6 -5) можно преобразовать следующим образом: • и, подставив X = Rm и ХAB = RABm, получить • т. е. в этом случае расчет можно вести по активным сопротивлениям, производя его отдельно для вещественной и мнимой частей:

• Однородная линия с постоянным сечением проводов • При одинаковом сечении проводов однородной линии по всей длине, т. е. при r 0 = const, что практически встречается часто, мы можем, заменив в формуле (6 -7) Ri=r 0 Li и RAB = r 0 LAB, где Li — расстояния от соответствующих нагрузок до пункта В, a LAB — длина всей линии, получить: • В этом случае расчет можно вести по длинам, определяя распределение отдельно активных и отдельно реактивных нагрузок.

Линии с нагрузками, имеющими одинаковый коэффициент мощности. • Если cos f всех нагрузок одинаков и линии однородны, то расчет можно вести по формуле (6 -7), подставляя в нее величины полных мощностей. При чисто активной нагрузке (cos f = 1) в эту формулу подставляются активные нагрузки.

6. 4. Порядок расчета простых замкнутых сетей • Расчет простых замкнутых сетей, в отличие от расчета радиальных линий, должен сопровождаться проверкой сетей в двух режимах: нормальном, когда потребители одновременно получают питание от двух источников питания A и В (рис. 6 -5, а), и аварийном, когда один из источников питания, например источник В, или же линия, к нему присоединенная, вышли из строя (рис. 6 -5, б).

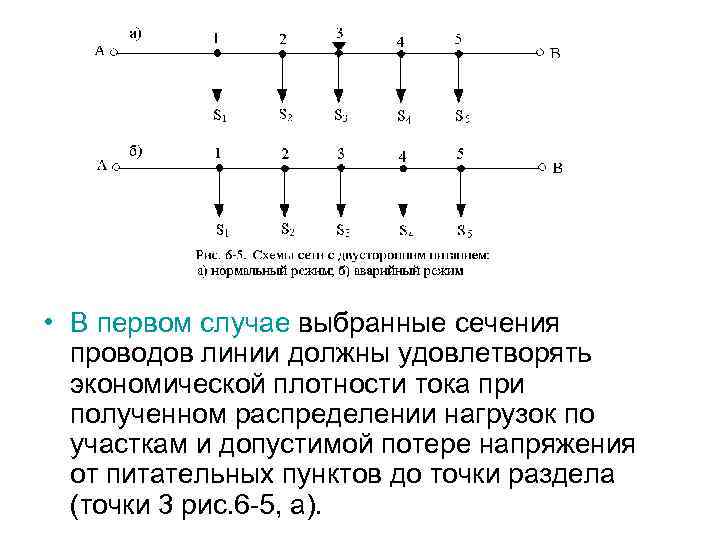• В первом случае выбранные сечения проводов линии должны удовлетворять экономической плотности тока при полученном распределении нагрузок по участкам и допустимой потере напряжения от питательных пунктов до точки раздела (точки 3 рис. 6 -5, а).

• Во втором случае должна быть выдержана допустимая потеря напряжения для аварийного режима до наиболее удаленной точки (точки 5 рис. 6 -5, б). Так как аварийные режимы не являются длительными, то в этих случаях сечение проводов может и не удовлетворять требованиям экономической плотности тока, но должно быть проверено по допустимому току на нагрев (см. гл. 3).

• При расчете замкнутых сетей с двусторонним питанием могут встретиться два характерных случая: • а) линия на всей длине выполнена одним сечением провода; • б) на участках, лежащих ближе к источникам питания, применен провод большего сечения, а на участках, примыкающих к точке раздела, — провод меньшего сечения.

• Первый случай встречается чаще, так как одинаковое сечение вдоль всей линии имеет практические удобства, о которых упоминалось в 4. 7. Такое решение с экономической точки зрения оправдывается при большом количестве нагрузок, присоединяемых к линии на сравнительно близких расстояниях друг от друга, а также при равномерной нагрузке по всей длине.

• Порядок расчета следующий. В нормальном режиме работы линии по формуле (6 -8) находят распределение мощности по участкам. Определяя токи на магистральных участках, по ним находят экономическое сечение, пользуясь формулами (2 -19) и (2 -20) для определения экономического сечения линии с равномерно распределенной нагрузкой. Из полученных экономических сечений принимают среднее, округляя его до ближайшего стандартного.

• Погрешность в определении экономического сечения в случае неравномерной нагрузки линии практически находится в допустимых пределах и тем меньше, чем больше нагрузок и чем чаще они расположены на линии. • После определения сечения проводов линии по формуле (2 -18) находят потерю напряжения до точки раздела и в случае превышения допустимой величины в нормальном режиме корректируют выбранное сечение.

• Затем рассматривают аварийный режим. Наиболее тяжелым случаем аварийного режима является отключение одного из источников питания. В этом случае питание всех нагрузок будет происходить с одной стороны. После определения распределения нагрузок по участкам находят потерю напряжения до наиболее удаленной точки и проверяют выбранное сечение проводов по нагреву.

• В случае, если проверка показывает превышение допустимых потерь напряжения (см. 4. 1. ) или допустимого нагрева проводов в аварийном режиме, сечение проводов увеличивают. • Во втором случае, т. е. применении ступенчатого сечения проводов, ход расчета сети аналогичен вышеизложенному. При этом сечение проводов выбирают методом подбора.

• Сначала находят в нормальном режиме предварительное распределение мощности по участкам, предполагая линию однородной. Затем по найденному распределению мощности определяют экономическое сечение проводов каждого участка, проверяют их по нагреву в нормальном и аварийном режимах. После этого делают повторный расчет распределения мощности в нормальном режиме, пользуясь формулами (6 -4) или (6 -6) и проверяют выбранные сечения по допустимой потере напряжения в нормальном и аварийном режимах. Если выбранные сечения не удовлетворяют допустимым величинам, их корректируют и повторяют расчет снова.

• В случаях, когда точки раздела активных и реактивных мощностей в нормальном режиме не совпадают друг с другом, для определения наибольшей потери напряжения делают расчеты до одной и другой точек раздела и судят о правильности выбранного сечения провода по большей величине.

• В замкнутых сетях, имеющих ответвления, наибольшие потери напряжения могут оказаться не в точке раздела, а на наиболее удаленной точке ответвления. Сечения проводов на ответвлениях определяют методами расчета радиальных сетей, исходя из располагаемых допустимых потерь напряжения от точки ответвления до наиболее удаленной точки.