6 Основы теории НДС.ppt
- Количество слайдов: 81
 6. Основы теории напряженно-деформированного состояния
6. Основы теории напряженно-деформированного состояния
 При рассмотрении вопросов этой темы воспользуемся решениями, полученными в курсе «Теория упругости» , с учетом традиционных для сопротивления материалов допущений и гипотез. Из рассмотрения предыдущих разделов мы уже знаем, что взаимодействие между конструкциями и их элементами характеризуется внешними силами и, как следствие, внутренними силовыми факторами в различных сечениях, напряжениями и деформациями, которые будут иметь различные значения в разных точках по разным направлениям.
При рассмотрении вопросов этой темы воспользуемся решениями, полученными в курсе «Теория упругости» , с учетом традиционных для сопротивления материалов допущений и гипотез. Из рассмотрения предыдущих разделов мы уже знаем, что взаимодействие между конструкциями и их элементами характеризуется внешними силами и, как следствие, внутренними силовыми факторами в различных сечениях, напряжениями и деформациями, которые будут иметь различные значения в разных точках по разным направлениям.
 Прочность и жесткость конструкции и ее элементов определяют значения напряжений и деформаций. Величина и направление этих напряжений и деформаций зависит не только от ВСФ, но и от положения плоскости, по которой их определяют. Как известно, через точку можно провести сколь угодно много плоскостей.
Прочность и жесткость конструкции и ее элементов определяют значения напряжений и деформаций. Величина и направление этих напряжений и деформаций зависит не только от ВСФ, но и от положения плоскости, по которой их определяют. Как известно, через точку можно провести сколь угодно много плоскостей.
 Совокупность напряжений, действующих по различным площадкам, проведенным через исследуемую точку – напряженное состояние в точке. Совокупность деформаций, возникающих в исследуемой точке по различным направлениям и по различным плоскостям – деформированное состояние в точке.
Совокупность напряжений, действующих по различным площадкам, проведенным через исследуемую точку – напряженное состояние в точке. Совокупность деформаций, возникающих в исследуемой точке по различным направлениям и по различным плоскостям – деформированное состояние в точке.
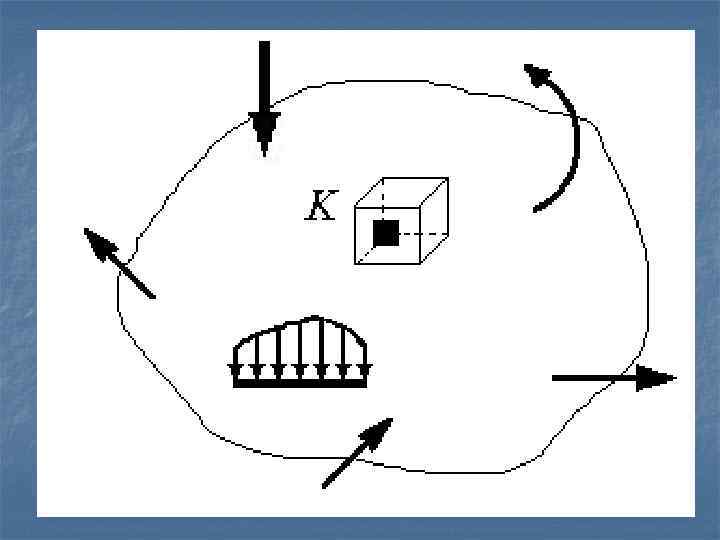
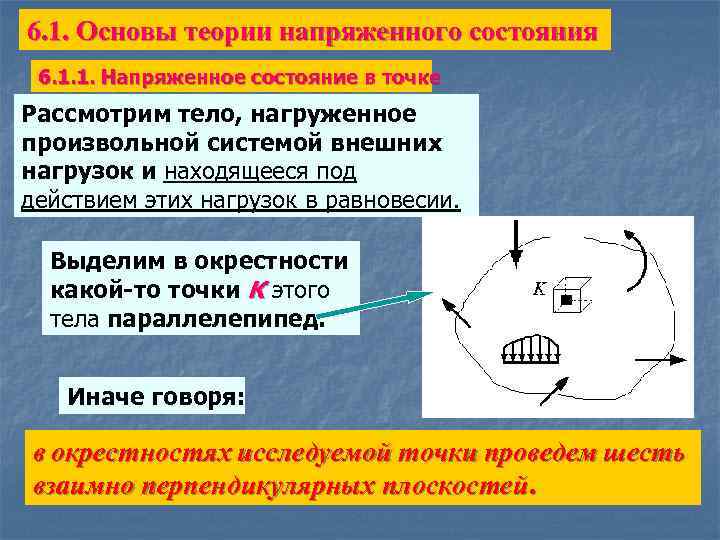 6. 1. Основы теории напряженного состояния 6. 1. 1. Напряженное состояние в точке Рассмотрим тело, нагруженное произвольной системой внешних нагрузок и находящееся под действием этих нагрузок в равновесии. Выделим в окрестности какой-то точки К этого тела параллелепипед. Иначе говоря: в окрестностях исследуемой точки проведем шесть взаимно перпендикулярных плоскостей.
6. 1. Основы теории напряженного состояния 6. 1. 1. Напряженное состояние в точке Рассмотрим тело, нагруженное произвольной системой внешних нагрузок и находящееся под действием этих нагрузок в равновесии. Выделим в окрестности какой-то точки К этого тела параллелепипед. Иначе говоря: в окрестностях исследуемой точки проведем шесть взаимно перпендикулярных плоскостей.
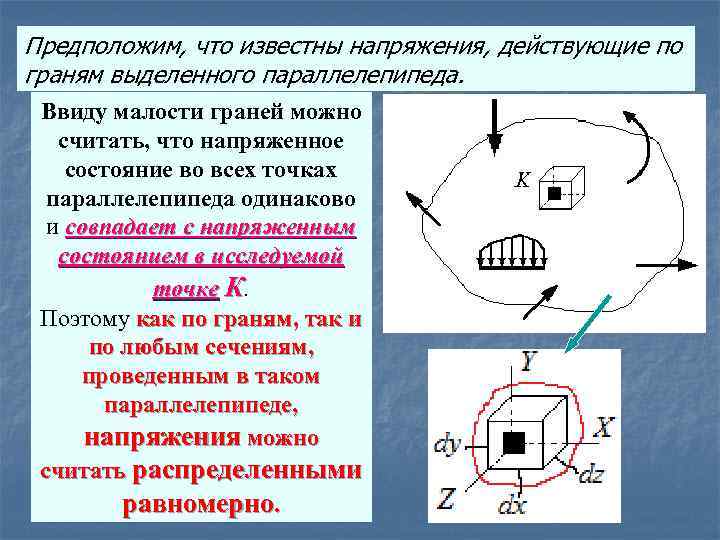 Предположим, что известны напряжения, действующие по граням выделенного параллелепипеда. Ввиду малости граней можно считать, что напряженное состояние во всех точках параллелепипеда одинаково и совпадает с напряженным состоянием в исследуемой точке К. Поэтому как по граням, так и по любым сечениям, проведенным в таком параллелепипеде, напряжения можно считать распределенными равномерно.
Предположим, что известны напряжения, действующие по граням выделенного параллелепипеда. Ввиду малости граней можно считать, что напряженное состояние во всех точках параллелепипеда одинаково и совпадает с напряженным состоянием в исследуемой точке К. Поэтому как по граням, так и по любым сечениям, проведенным в таком параллелепипеде, напряжения можно считать распределенными равномерно.
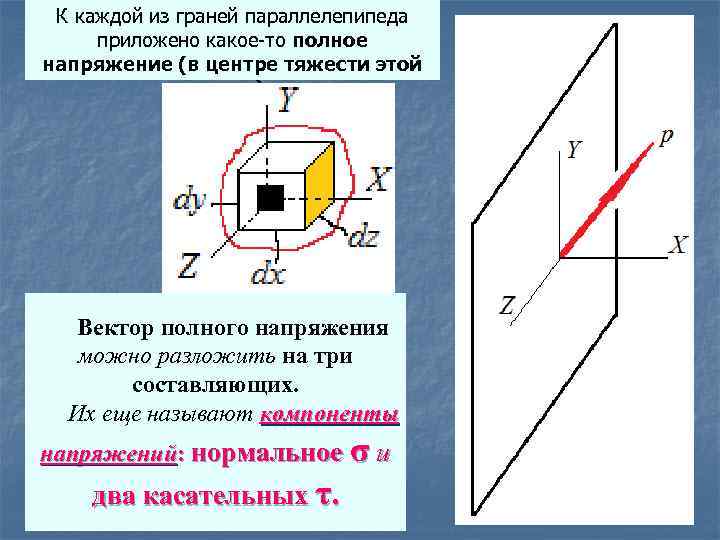 К каждой из граней параллелепипеда приложено какое-то полное напряжение (в центре тяжести этой грани). Вектор полного напряжения можно разложить на три составляющих. Их еще называют компоненты напряжений: нормальное σ и два касательных τ.
К каждой из граней параллелепипеда приложено какое-то полное напряжение (в центре тяжести этой грани). Вектор полного напряжения можно разложить на три составляющих. Их еще называют компоненты напряжений: нормальное σ и два касательных τ.
 Вектора компонент напряжений обозначают в соответствии с правилами, принятыми в теории упругости. σ Нормальным напряжениям присваиваем индексы в соответствии с осями, которым они параллельны: σx, σy, σz. Касательные напряжения τ: первый индекс – соответствует оси, которой параллелен вектор этого напряжения, т. е. направлению оси, параллельно которой оно действует; второй индекс – соответствует оси, которая перпендикулярна площадке (соответствует индексу при σ).
Вектора компонент напряжений обозначают в соответствии с правилами, принятыми в теории упругости. σ Нормальным напряжениям присваиваем индексы в соответствии с осями, которым они параллельны: σx, σy, σz. Касательные напряжения τ: первый индекс – соответствует оси, которой параллелен вектор этого напряжения, т. е. направлению оси, параллельно которой оно действует; второй индекс – соответствует оси, которая перпендикулярна площадке (соответствует индексу при σ).
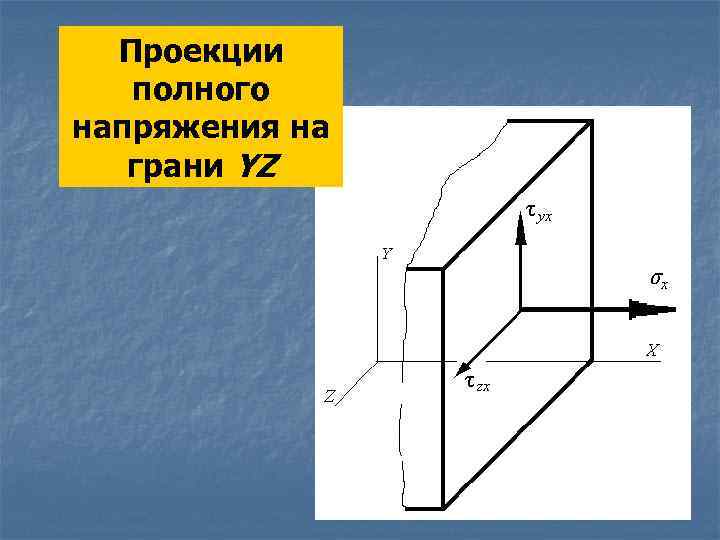 Проекции полного напряжения на грани YZ
Проекции полного напряжения на грани YZ
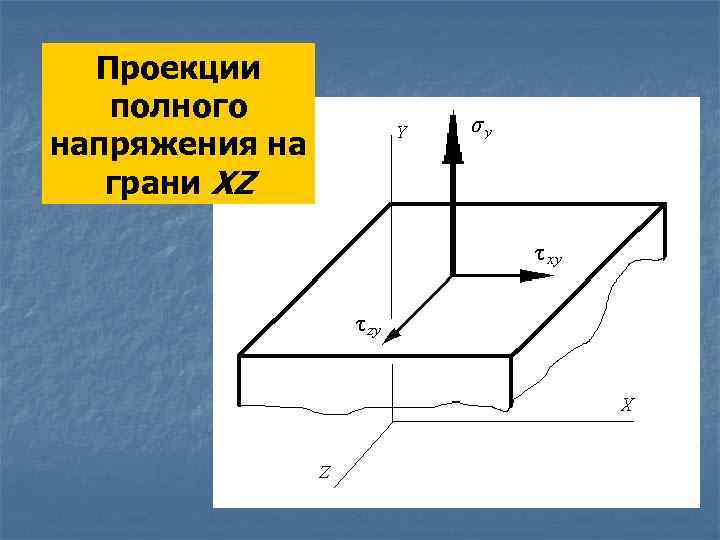 Проекции полного напряжения на грани XZ
Проекции полного напряжения на грани XZ
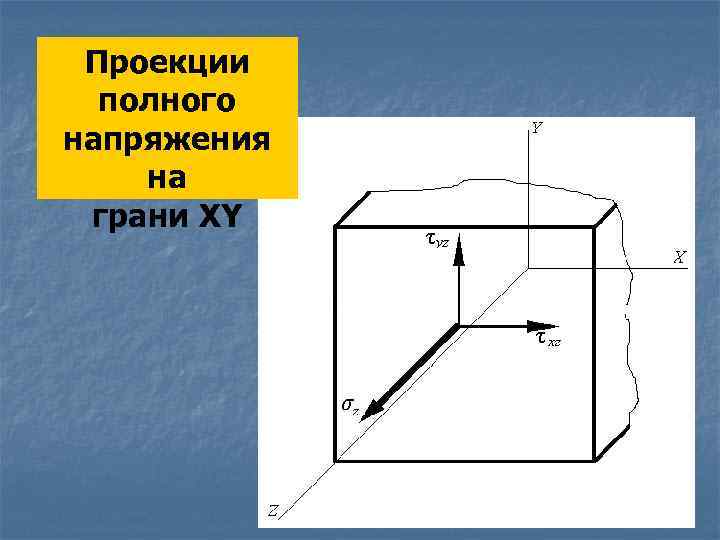 Проекции полного напряжения на грани XY
Проекции полного напряжения на грани XY
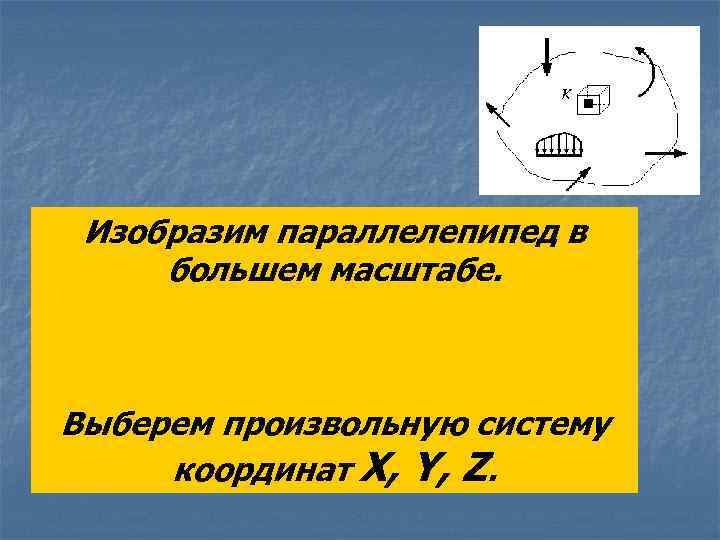 Изобразим параллелепипед в большем масштабе. Выберем произвольную систему координат X, Y, Z.
Изобразим параллелепипед в большем масштабе. Выберем произвольную систему координат X, Y, Z.
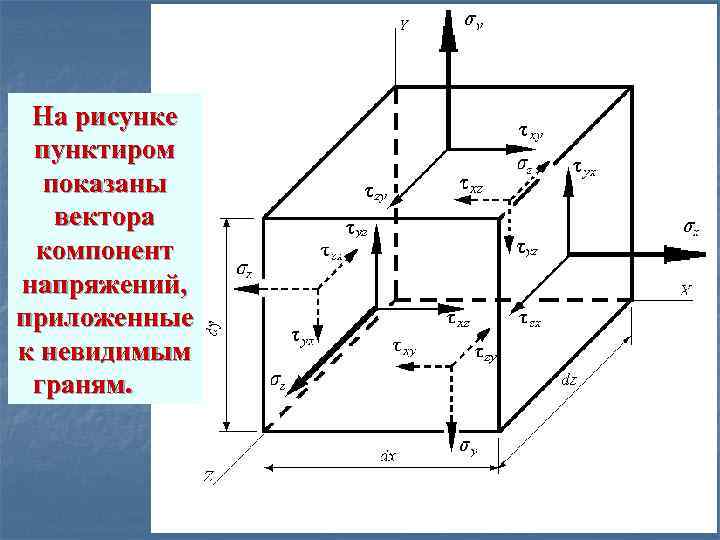 На рисунке пунктиром показаны вектора компонент напряжений, приложенные к невидимым граням.
На рисунке пунктиром показаны вектора компонент напряжений, приложенные к невидимым граням.
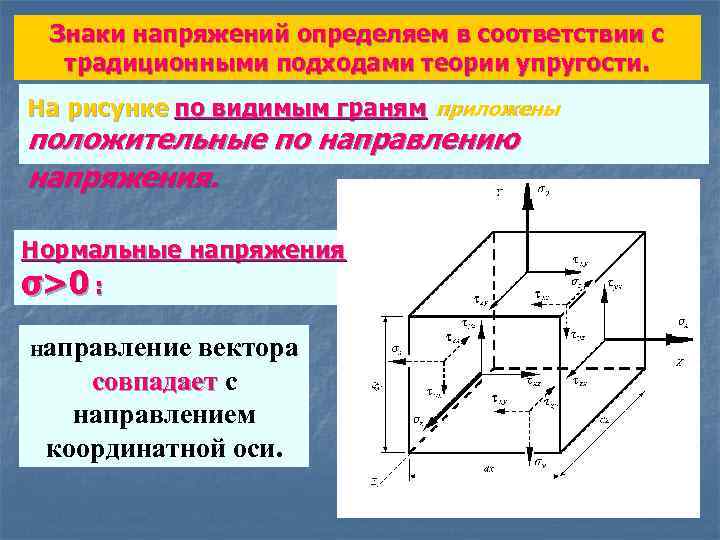 Знаки напряжений определяем в соответствии с традиционными подходами теории упругости. На рисунке по видимым граням приложены положительные по направлению напряжения. Нормальные напряжения σ> 0 : направление вектора совпадает с направлением координатной оси.
Знаки напряжений определяем в соответствии с традиционными подходами теории упругости. На рисунке по видимым граням приложены положительные по направлению напряжения. Нормальные напряжения σ> 0 : направление вектора совпадает с направлением координатной оси.
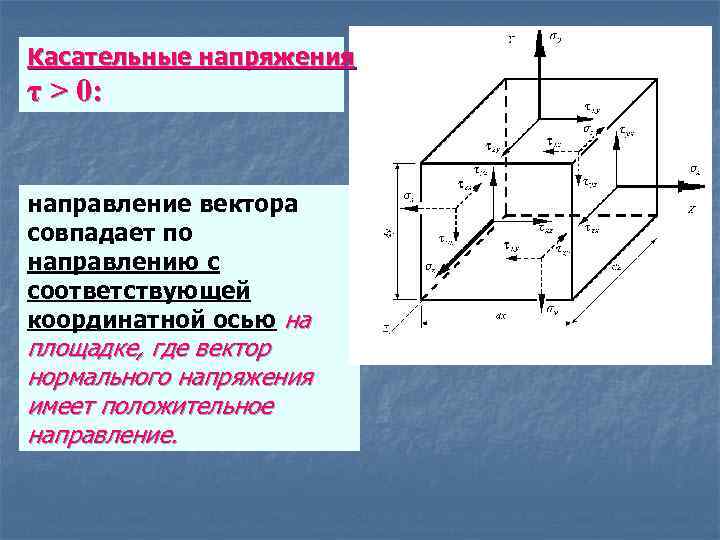 Касательные напряжения τ > 0: направление вектора совпадает по направлению с соответствующей координатной осью на площадке, где вектор нормального напряжения имеет положительное направление.
Касательные напряжения τ > 0: направление вектора совпадает по направлению с соответствующей координатной осью на площадке, где вектор нормального напряжения имеет положительное направление.
 Таким образом, по шести граням действуют: 6∙ 3=18 компонент напряжений. На параллельных гранях по условиям равновесия напряжения равны попарно. Поэтому количество неизвестных напряжений равно девяти: σ и шесть три τ.
Таким образом, по шести граням действуют: 6∙ 3=18 компонент напряжений. На параллельных гранях по условиям равновесия напряжения равны попарно. Поэтому количество неизвестных напряжений равно девяти: σ и шесть три τ.
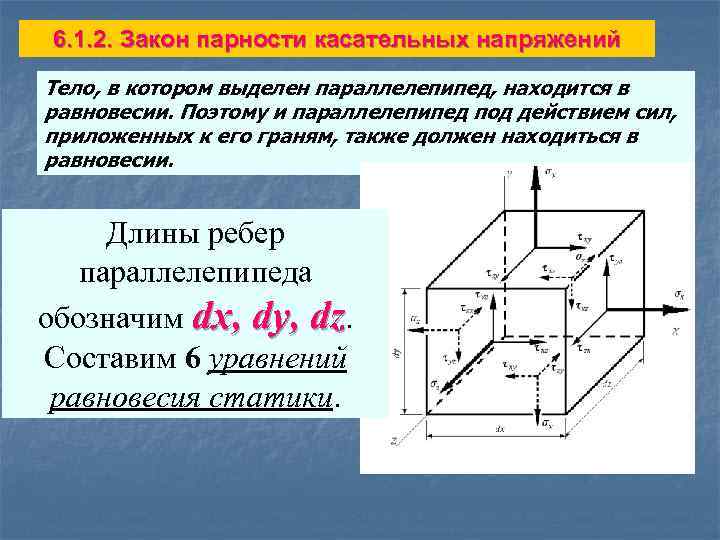 6. 1. 2. Закон парности касательных напряжений Тело, в котором выделен параллелепипед, находится в равновесии. Поэтому и параллелепипед под действием сил, приложенных к его граням, также должен находиться в равновесии. Длины ребер параллелепипеда обозначим dx, dy, dz. Составим 6 уравнений равновесия статики.
6. 1. 2. Закон парности касательных напряжений Тело, в котором выделен параллелепипед, находится в равновесии. Поэтому и параллелепипед под действием сил, приложенных к его граням, также должен находиться в равновесии. Длины ребер параллелепипеда обозначим dx, dy, dz. Составим 6 уравнений равновесия статики.
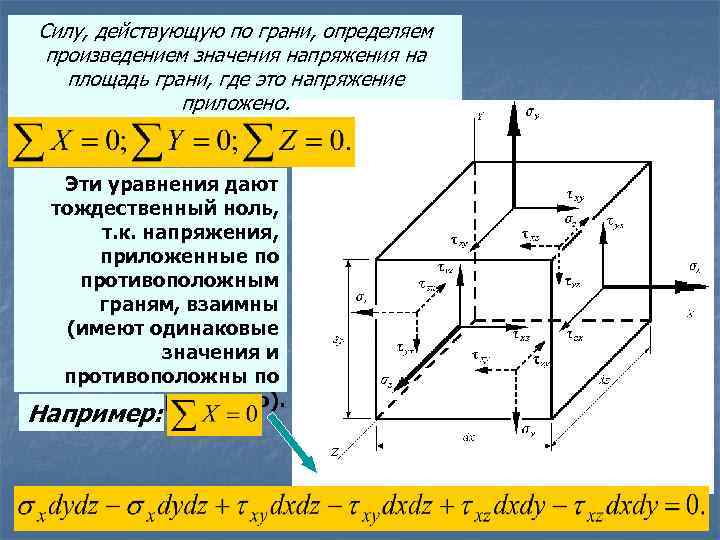 Силу, действующую по грани, определяем произведением значения напряжения на площадь грани, где это напряжение приложено. Эти уравнения дают тождественный ноль, т. к. напряжения, приложенные по противоположным граням, взаимны (имеют одинаковые значения и противоположны по направлению). Например:
Силу, действующую по грани, определяем произведением значения напряжения на площадь грани, где это напряжение приложено. Эти уравнения дают тождественный ноль, т. к. напряжения, приложенные по противоположным граням, взаимны (имеют одинаковые значения и противоположны по направлению). Например:
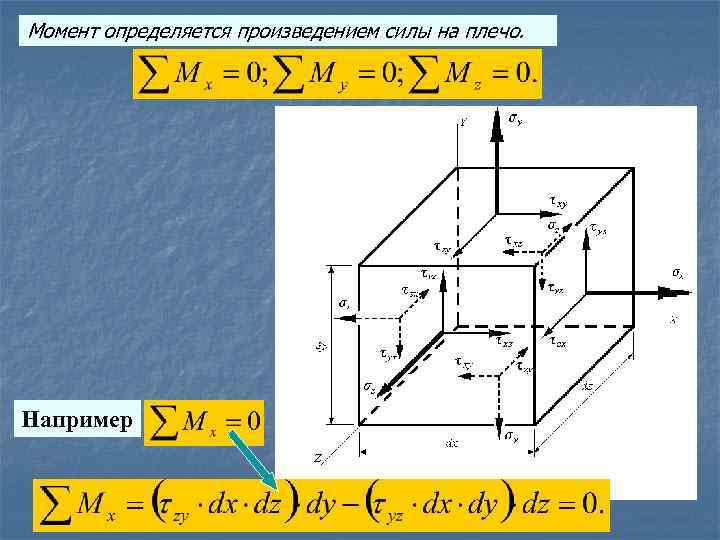 Момент определяется произведением силы на плечо. Например
Момент определяется произведением силы на плечо. Например
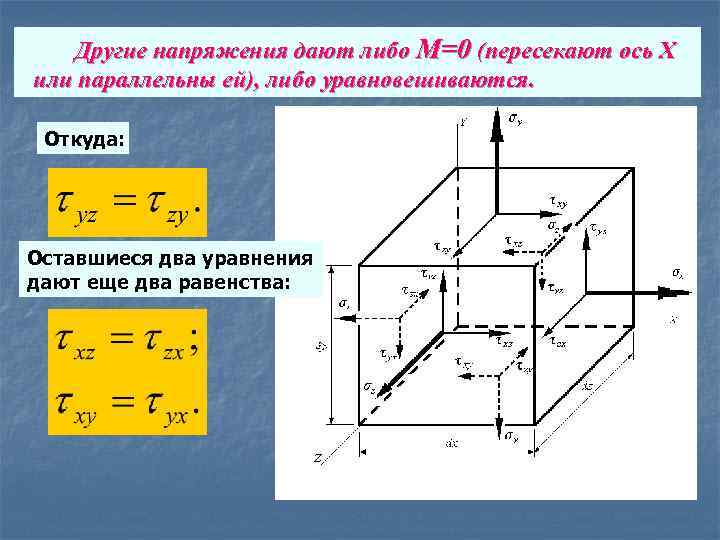 Другие напряжения дают либо M=0 (пересекают ось X или параллельны ей), либо уравновешиваются. Откуда: Оставшиеся два уравнения дают еще два равенства:
Другие напряжения дают либо M=0 (пересекают ось X или параллельны ей), либо уравновешиваются. Откуда: Оставшиеся два уравнения дают еще два равенства:
 Закон парности касательных напряжений: Касательные напряжения, действующие по двум взаимно перпендикулярным площадкам и перпендикулярные к общему ребру, равны по величине и направлены либо к ребру, либо от ребра.
Закон парности касательных напряжений: Касательные напряжения, действующие по двум взаимно перпендикулярным площадкам и перпендикулярные к общему ребру, равны по величине и направлены либо к ребру, либо от ребра.
 Таким образом, остаются неизвестными шесть компонент напряжений: Из этих компонент напряжений (и парных им) составляют матрицу, которая называется: тензор напряжений
Таким образом, остаются неизвестными шесть компонент напряжений: Из этих компонент напряжений (и парных им) составляют матрицу, которая называется: тензор напряжений
 6. 1. 3. Главные напряжения и главные площадки При изменении положения выделенного элемента (при его повороте в пространстве) напряжения на его гранях также будут изменять свою величину и направление. В теории упругости доказано, что всегда можно найти такое положение элемента, при котором на его гранях τ будут отсутствовать, т. е. равняться нулю.
6. 1. 3. Главные напряжения и главные площадки При изменении положения выделенного элемента (при его повороте в пространстве) напряжения на его гранях также будут изменять свою величину и направление. В теории упругости доказано, что всегда можно найти такое положение элемента, при котором на его гранях τ будут отсутствовать, т. е. равняться нулю.
 Площадки, по которым не действуют τ, называются главными площадками, а нормальные напряжения σ на этих площадках – главными напряжениями. В теории упругости также доказывается, что в каждой точке любым образом нагруженного тела всегда имеются три главные взаимно перпендикулярные площадки.
Площадки, по которым не действуют τ, называются главными площадками, а нормальные напряжения σ на этих площадках – главными напряжениями. В теории упругости также доказывается, что в каждой точке любым образом нагруженного тела всегда имеются три главные взаимно перпендикулярные площадки.
 Главные напряжения принято обозначать σ1, σ2, σ3, при этом полагают, что в алгебраическом смысле: Например: расчетом определены следующие значения нормальных напряжений: – 1000 МПа, 600 МПа, 100 МПа. Касательные напряжения равны нулю. Тогда:
Главные напряжения принято обозначать σ1, σ2, σ3, при этом полагают, что в алгебраическом смысле: Например: расчетом определены следующие значения нормальных напряжений: – 1000 МПа, 600 МПа, 100 МПа. Касательные напряжения равны нулю. Тогда:
 6. 1. 4. Виды напряженного состояния Вид напряженного состояния определяется количеством действующих главных напряжений. 1). Линейное (одноосное) напряженное состояние К граням элементарного параллелепипеда приложено только одно нормальное напряжение. Остальные два равны нулю.
6. 1. 4. Виды напряженного состояния Вид напряженного состояния определяется количеством действующих главных напряжений. 1). Линейное (одноосное) напряженное состояние К граням элементарного параллелепипеда приложено только одно нормальное напряжение. Остальные два равны нулю.
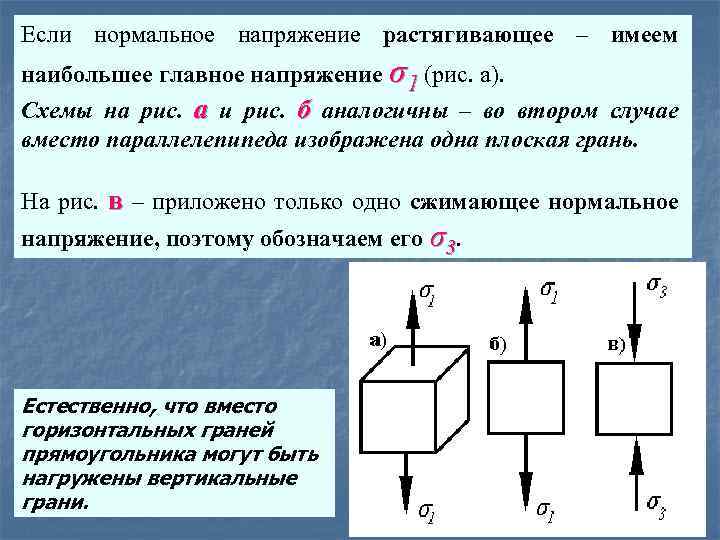 Если нормальное напряжение растягивающее – имеем наибольшее главное напряжение σ1 (рис. а). Схемы на рис. а и рис. б аналогичны – во втором случае вместо параллелепипеда изображена одна плоская грань. На рис. в – приложено только одно сжимающее нормальное напряжение, поэтому обозначаем его σ3. Естественно, что вместо горизонтальных граней прямоугольника могут быть нагружены вертикальные грани.
Если нормальное напряжение растягивающее – имеем наибольшее главное напряжение σ1 (рис. а). Схемы на рис. а и рис. б аналогичны – во втором случае вместо параллелепипеда изображена одна плоская грань. На рис. в – приложено только одно сжимающее нормальное напряжение, поэтому обозначаем его σ3. Естественно, что вместо горизонтальных граней прямоугольника могут быть нагружены вертикальные грани.
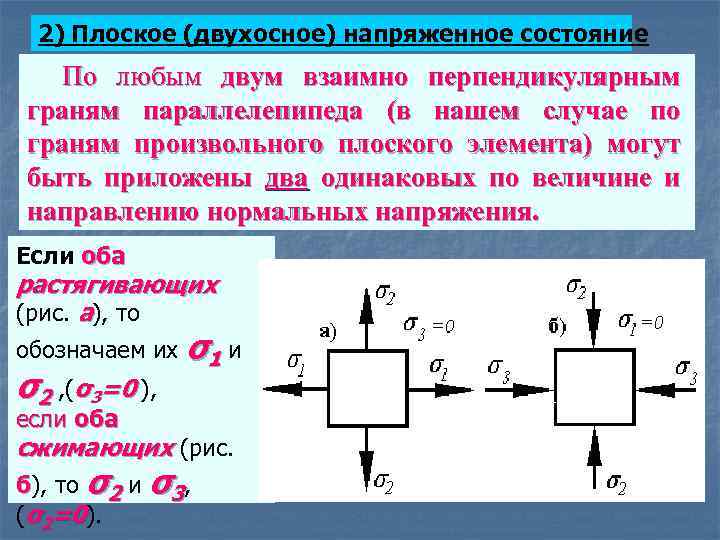 2) Плоское (двухосное) напряженное состояние По любым двум взаимно перпендикулярным граням параллелепипеда (в нашем случае по граням произвольного плоского элемента) могут быть приложены два одинаковых по величине и направлению нормальных напряжения. Если оба растягивающих (рис. а), то обозначаем их σ2 , (σ3=0 ), σ1 и если оба сжимающих (рис. б), то σ2 и (σ2=0). σ3 ,
2) Плоское (двухосное) напряженное состояние По любым двум взаимно перпендикулярным граням параллелепипеда (в нашем случае по граням произвольного плоского элемента) могут быть приложены два одинаковых по величине и направлению нормальных напряжения. Если оба растягивающих (рис. а), то обозначаем их σ2 , (σ3=0 ), σ1 и если оба сжимающих (рис. б), то σ2 и (σ2=0). σ3 ,
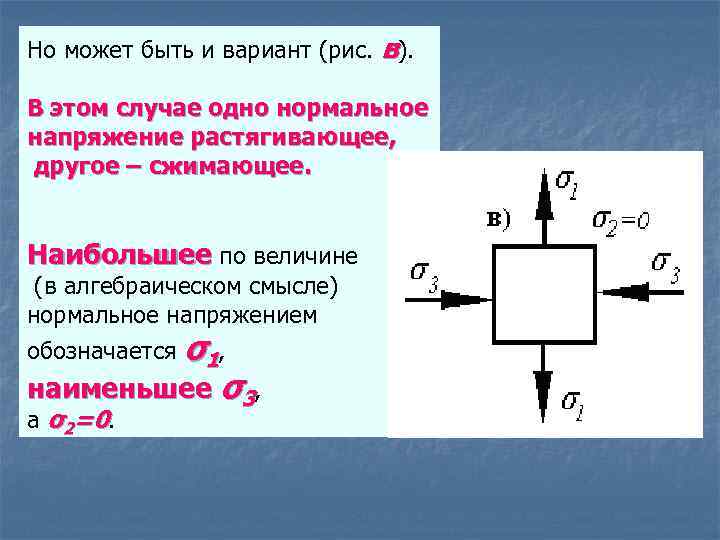 Но может быть и вариант (рис. в). В этом случае одно нормальное напряжение растягивающее, другое – сжимающее. Наибольшее по величине (в алгебраическом смысле) нормальное напряжением σ1 , наименьшее σ3, обозначается а σ2=0.
Но может быть и вариант (рис. в). В этом случае одно нормальное напряжение растягивающее, другое – сжимающее. Наибольшее по величине (в алгебраическом смысле) нормальное напряжением σ1 , наименьшее σ3, обозначается а σ2=0.
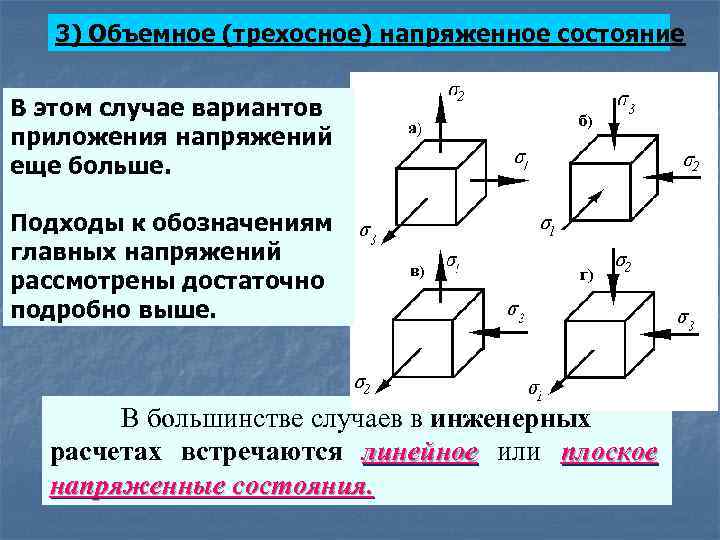 3) Объемное (трехосное) напряженное состояние В этом случае вариантов приложения напряжений еще больше. Подходы к обозначениям главных напряжений рассмотрены достаточно подробно выше. В большинстве случаев в инженерных расчетах встречаются линейное или плоское напряженные состояния.
3) Объемное (трехосное) напряженное состояние В этом случае вариантов приложения напряжений еще больше. Подходы к обозначениям главных напряжений рассмотрены достаточно подробно выше. В большинстве случаев в инженерных расчетах встречаются линейное или плоское напряженные состояния.
 Рассмотрим более подробно теоретические предпосылки определения главных напряжений и напряжений, действующих по любым (произвольным) площадкам. В теории напряженного состояния рассматривается решение двух типов задач: – прямая задача. По известным в точке главным напряжениям требуется определить нормальные и касательные напряжения по площадкам, наклоненным под заданным углом к главным площадкам. – обратная задача. По известным нормальным и касательным напряжениям, действующим в двух взаимно перпендикулярных площадках, проходящих через данную точку, требуется найти главные напряжения.
Рассмотрим более подробно теоретические предпосылки определения главных напряжений и напряжений, действующих по любым (произвольным) площадкам. В теории напряженного состояния рассматривается решение двух типов задач: – прямая задача. По известным в точке главным напряжениям требуется определить нормальные и касательные напряжения по площадкам, наклоненным под заданным углом к главным площадкам. – обратная задача. По известным нормальным и касательным напряжениям, действующим в двух взаимно перпендикулярных площадках, проходящих через данную точку, требуется найти главные напряжения.
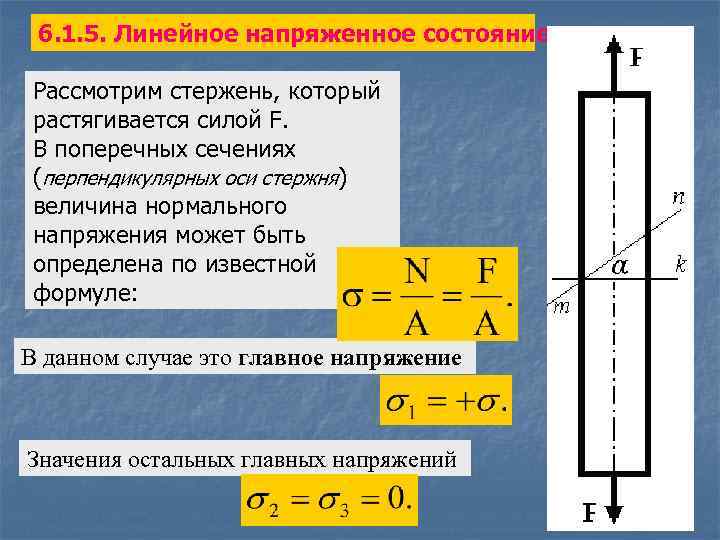 6. 1. 5. Линейное напряженное состояние Рассмотрим стержень, который растягивается силой F. В поперечных сечениях (перпендикулярных оси стержня) величина нормального напряжения может быть определена по известной формуле: В данном случае это главное напряжение Значения остальных главных напряжений
6. 1. 5. Линейное напряженное состояние Рассмотрим стержень, который растягивается силой F. В поперечных сечениях (перпендикулярных оси стержня) величина нормального напряжения может быть определена по известной формуле: В данном случае это главное напряжение Значения остальных главных напряжений
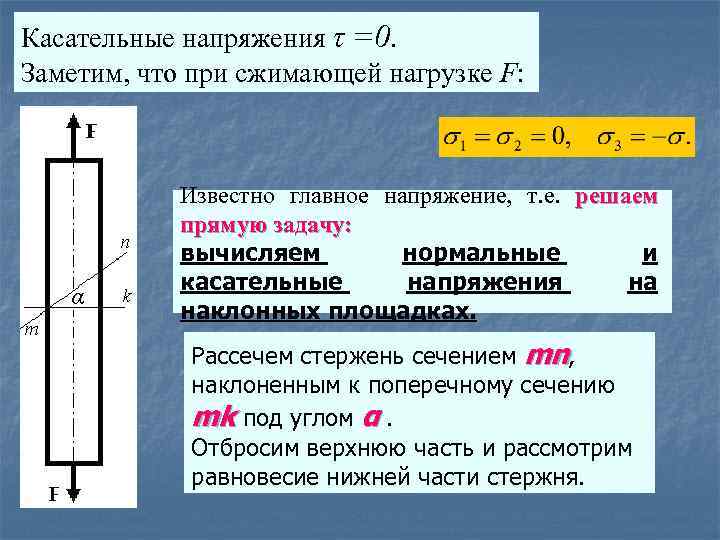 Касательные напряжения τ =0. Заметим, что при сжимающей нагрузке F: Известно главное напряжение, т. е. решаем прямую задачу: вычисляем нормальные и касательные напряжения на наклонных площадках. Рассечем стержень сечением mn, наклоненным к поперечному сечению mk под углом α. Отбросим верхнюю часть и рассмотрим равновесие нижней части стержня.
Касательные напряжения τ =0. Заметим, что при сжимающей нагрузке F: Известно главное напряжение, т. е. решаем прямую задачу: вычисляем нормальные и касательные напряжения на наклонных площадках. Рассечем стержень сечением mn, наклоненным к поперечному сечению mk под углом α. Отбросим верхнюю часть и рассмотрим равновесие нижней части стержня.
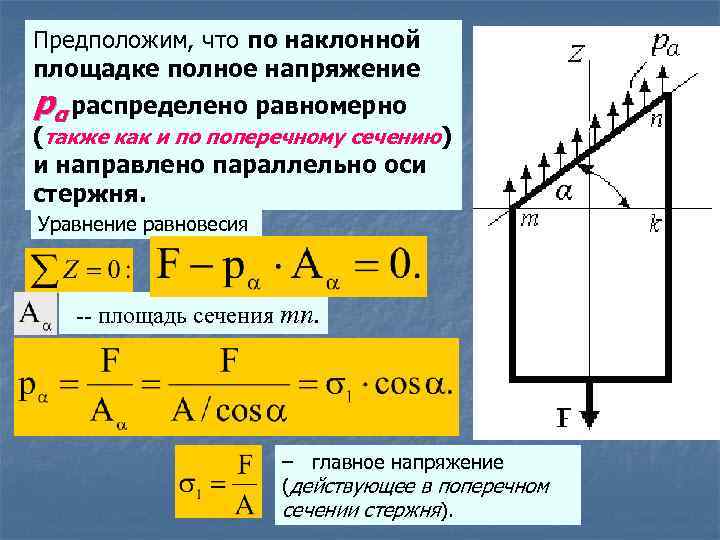 Предположим, что по наклонной площадке полное напряжение pα распределено равномерно (также как и по поперечному сечению) и направлено параллельно оси стержня. Уравнение равновесия -- площадь сечения mn. – главное напряжение (действующее в поперечном сечении стержня).
Предположим, что по наклонной площадке полное напряжение pα распределено равномерно (также как и по поперечному сечению) и направлено параллельно оси стержня. Уравнение равновесия -- площадь сечения mn. – главное напряжение (действующее в поперечном сечении стержня).
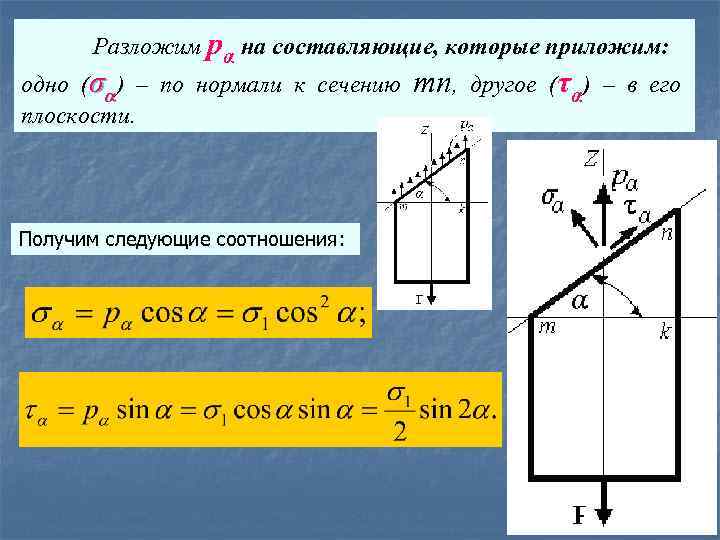 Разложим pα на составляющие, которые приложим: одно (σα) – по нормали к сечению плоскости. Получим следующие соотношения: mn, другое (τα) – в его
Разложим pα на составляющие, которые приложим: одно (σα) – по нормали к сечению плоскости. Получим следующие соотношения: mn, другое (τα) – в его
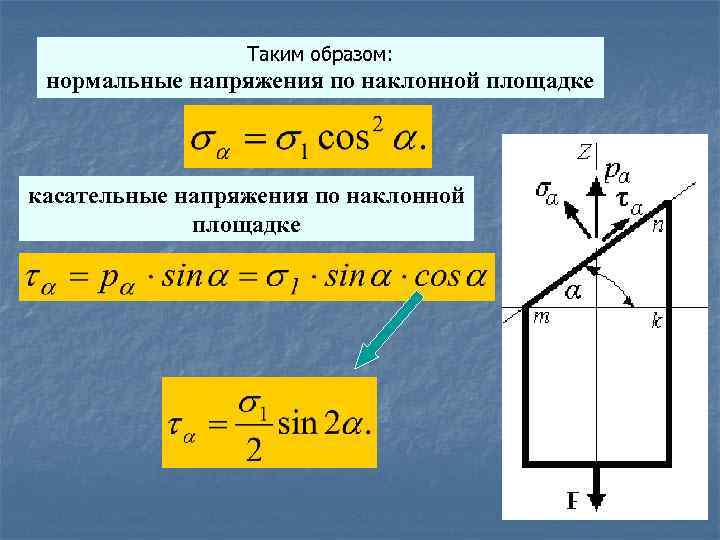 Таким образом: нормальные напряжения по наклонной площадке касательные напряжения по наклонной площадке
Таким образом: нормальные напряжения по наклонной площадке касательные напряжения по наклонной площадке
 Исследуем полученные формулы. 1) При cos 0 = 1; (в поперечных сечениях стержня): стержня sin 0 = 0; Касательные напряжения в поперечных сечениях не возникают. В поперечном сечении действуют максимальные нормальные напряжения. Поперечное сечение стержня – является главной площадкой.
Исследуем полученные формулы. 1) При cos 0 = 1; (в поперечных сечениях стержня): стержня sin 0 = 0; Касательные напряжения в поперечных сечениях не возникают. В поперечном сечении действуют максимальные нормальные напряжения. Поперечное сечение стержня – является главной площадкой.
 2) При (в сечениях, параллельных продольной оси стержня): стержня cos 90 = 0; sin 180 = 0; В продольных сечениях стержня напряжения отсутствуют.
2) При (в сечениях, параллельных продольной оси стержня): стержня cos 90 = 0; sin 180 = 0; В продольных сечениях стержня напряжения отсутствуют.
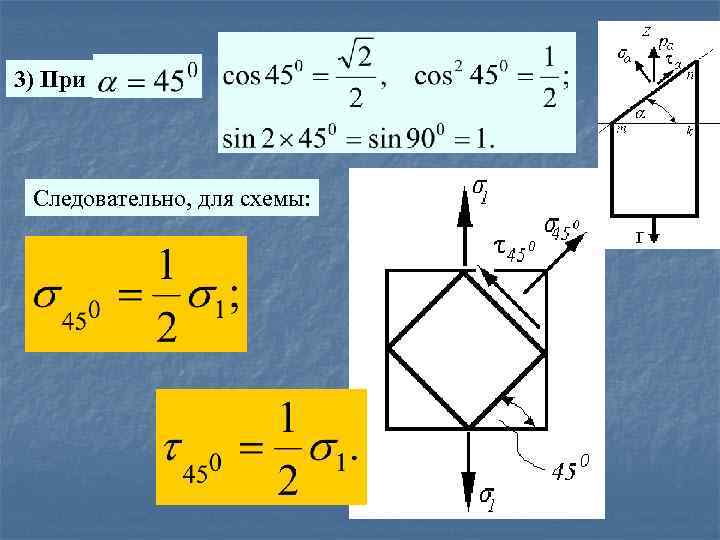 3) При Следовательно, для схемы:
3) При Следовательно, для схемы:
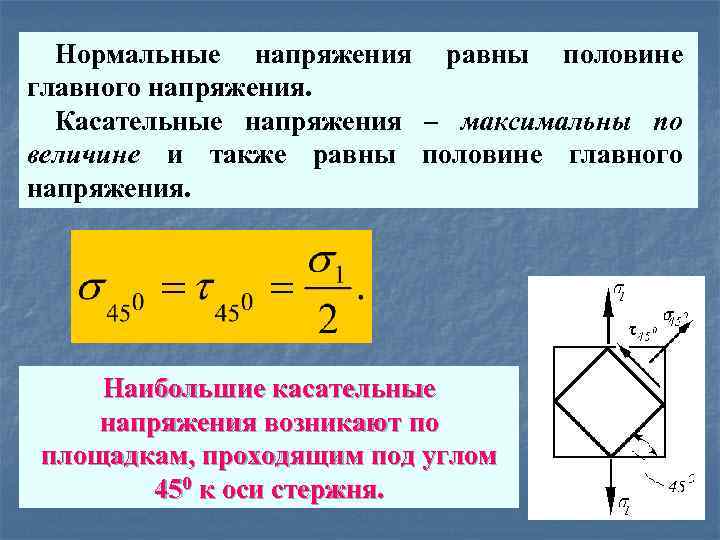 Нормальные напряжения равны половине главного напряжения. Касательные напряжения – максимальны по величине и также равны половине главного напряжения. Наибольшие касательные напряжения возникают по площадкам, проходящим под углом 450 к оси стержня.
Нормальные напряжения равны половине главного напряжения. Касательные напряжения – максимальны по величине и также равны половине главного напряжения. Наибольшие касательные напряжения возникают по площадкам, проходящим под углом 450 к оси стержня.
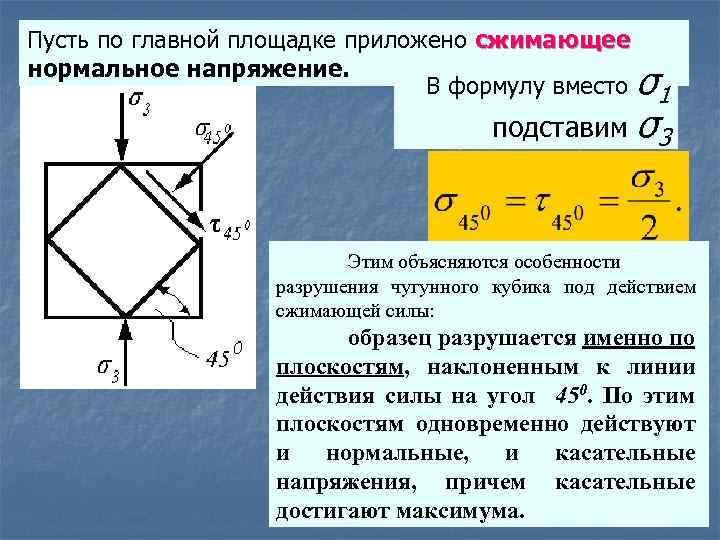 Пусть по главной площадке приложено сжимающее нормальное напряжение. В формулу вместо σ1 подставим σ3 Этим объясняются особенности разрушения чугунного кубика под действием сжимающей силы: образец разрушается именно по плоскостям, наклоненным к линии действия силы на угол 450. По этим плоскостям одновременно действуют и нормальные, и касательные напряжения, причем касательные достигают максимума.
Пусть по главной площадке приложено сжимающее нормальное напряжение. В формулу вместо σ1 подставим σ3 Этим объясняются особенности разрушения чугунного кубика под действием сжимающей силы: образец разрушается именно по плоскостям, наклоненным к линии действия силы на угол 450. По этим плоскостям одновременно действуют и нормальные, и касательные напряжения, причем касательные достигают максимума.
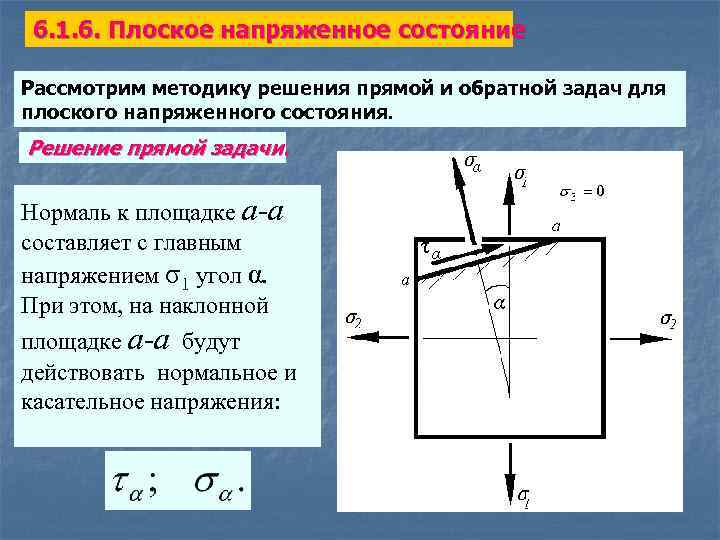 6. 1. 6. Плоское напряженное состояние Рассмотрим методику решения прямой и обратной задач для плоского напряженного состояния. Решение прямой задачи. Нормаль к площадке a-a составляет с главным напряжением σ1 угол α. При этом, на наклонной площадке a-a будут действовать нормальное и касательное напряжения:
6. 1. 6. Плоское напряженное состояние Рассмотрим методику решения прямой и обратной задач для плоского напряженного состояния. Решение прямой задачи. Нормаль к площадке a-a составляет с главным напряжением σ1 угол α. При этом, на наклонной площадке a-a будут действовать нормальное и касательное напряжения:
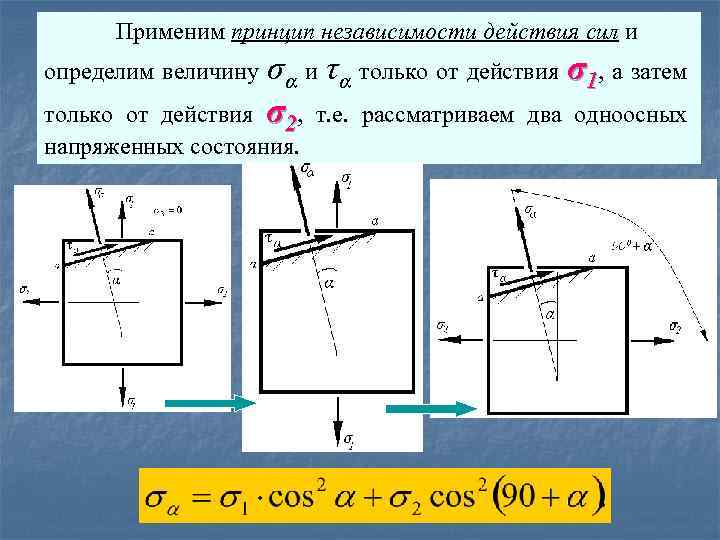 Применим принцип независимости действия сил и определим величину σα и τα только от действия σ1, а затем σ2, т. е. рассматриваем два одноосных только от действия напряженных состояния.
Применим принцип независимости действия сил и определим величину σα и τα только от действия σ1, а затем σ2, т. е. рассматриваем два одноосных только от действия напряженных состояния.
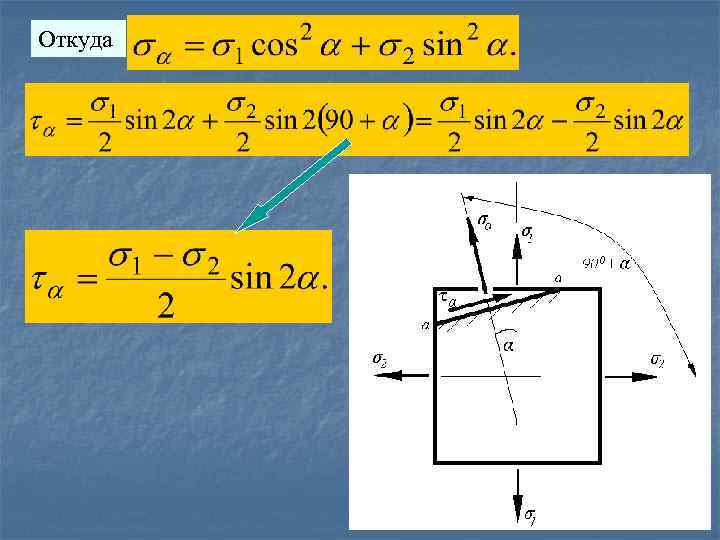 Откуда
Откуда
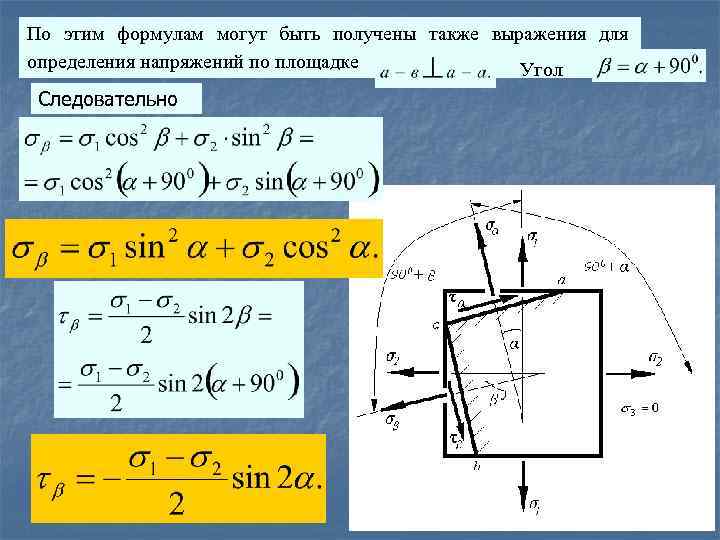 По этим формулам могут быть получены также выражения для определения напряжений по площадке Угол Следовательно
По этим формулам могут быть получены также выражения для определения напряжений по площадке Угол Следовательно
 Складывая почленно, получим: Сумма нормальных напряжений, действующих по двум произвольным и взаимно перпендикулярным площадкам постоянна и равна сумме главных напряжений, приложенных по главным площадкам, повернутым по отношению к произвольным. Сравнивая полученные формулы видим, что Получили еще одно доказательство закона парности касательных напряжений.
Складывая почленно, получим: Сумма нормальных напряжений, действующих по двум произвольным и взаимно перпендикулярным площадкам постоянна и равна сумме главных напряжений, приложенных по главным площадкам, повернутым по отношению к произвольным. Сравнивая полученные формулы видим, что Получили еще одно доказательство закона парности касательных напряжений.
 Касательные напряжения τα достигнут максимального значения при Максимальные касательные напряжения τ действуют по площадкам, наклоненным к главным площадкам под углом 450. Во все полученные выше формулы значения напряжений нужно подставлять со своим знаком.
Касательные напряжения τα достигнут максимального значения при Максимальные касательные напряжения τ действуют по площадкам, наклоненным к главным площадкам под углом 450. Во все полученные выше формулы значения напряжений нужно подставлять со своим знаком.
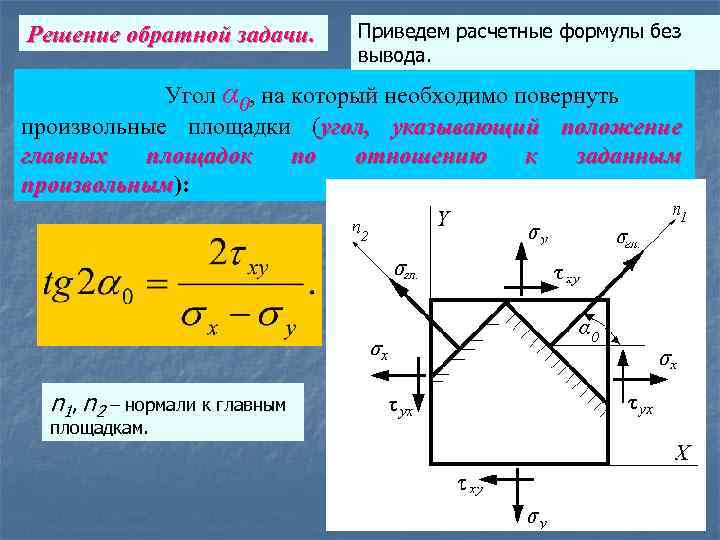 Решение обратной задачи. Приведем расчетные формулы без вывода. Угол α 0, на который необходимо повернуть произвольные площадки (угол, указывающий положение главных площадок по отношению к заданным произвольным): произвольным n 1, n 2 – нормали к главным площадкам.
Решение обратной задачи. Приведем расчетные формулы без вывода. Угол α 0, на который необходимо повернуть произвольные площадки (угол, указывающий положение главных площадок по отношению к заданным произвольным): произвольным n 1, n 2 – нормали к главным площадкам.
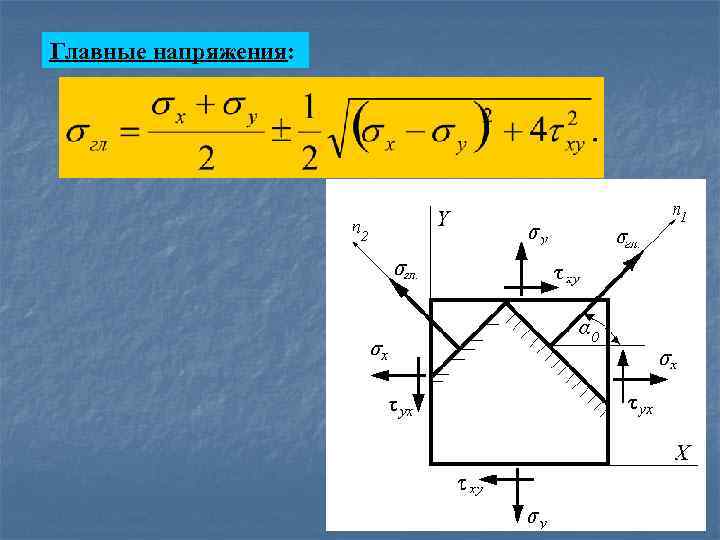 Главные напряжения:
Главные напряжения:
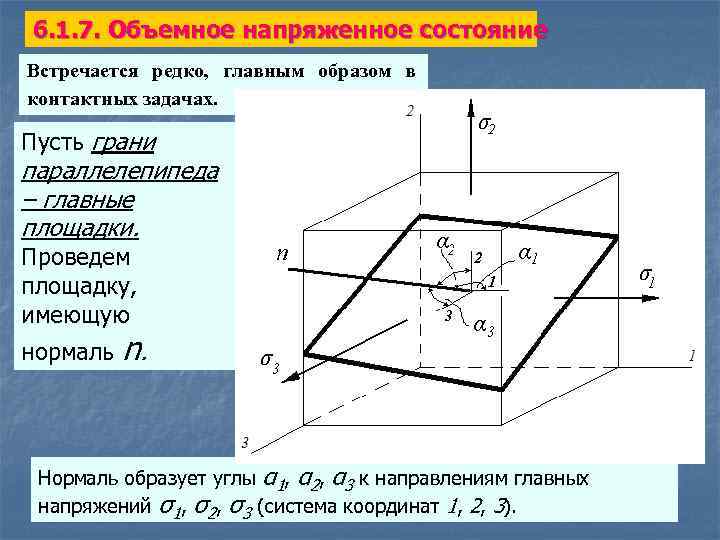 6. 1. 7. Объемное напряженное состояние Встречается редко, главным образом в контактных задачах. Пусть грани параллелепипеда – главные площадки. Проведем площадку, имеющую нормаль n. Нормаль образует углы α 1, α 2, α 3 к направлениям главных напряжений σ1, σ2, σ3 (система координат 1, 2, 3).
6. 1. 7. Объемное напряженное состояние Встречается редко, главным образом в контактных задачах. Пусть грани параллелепипеда – главные площадки. Проведем площадку, имеющую нормаль n. Нормаль образует углы α 1, α 2, α 3 к направлениям главных напряжений σ1, σ2, σ3 (система координат 1, 2, 3).
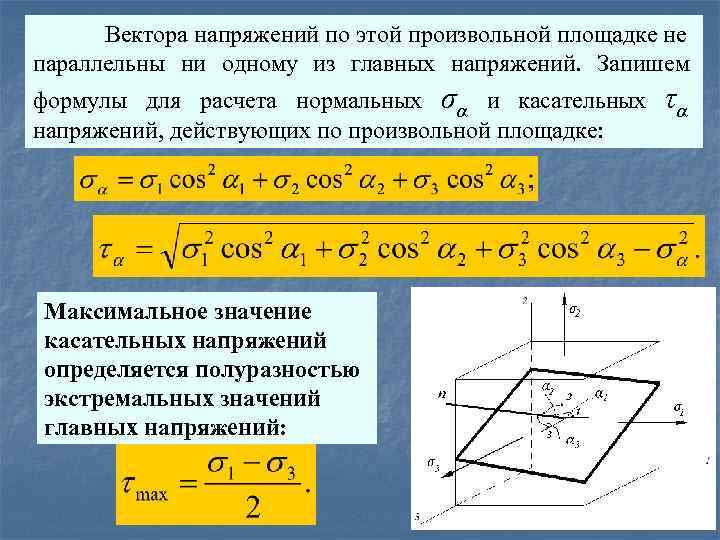 Вектора напряжений по этой произвольной площадке не параллельны ни одному из главных напряжений. Запишем формулы для расчета нормальных σα и касательных напряжений, действующих по произвольной площадке: Максимальное значение. касательных напряжений определяется полуразностью экстремальных значений главных напряжений: τα
Вектора напряжений по этой произвольной площадке не параллельны ни одному из главных напряжений. Запишем формулы для расчета нормальных σα и касательных напряжений, действующих по произвольной площадке: Максимальное значение. касательных напряжений определяется полуразностью экстремальных значений главных напряжений: τα
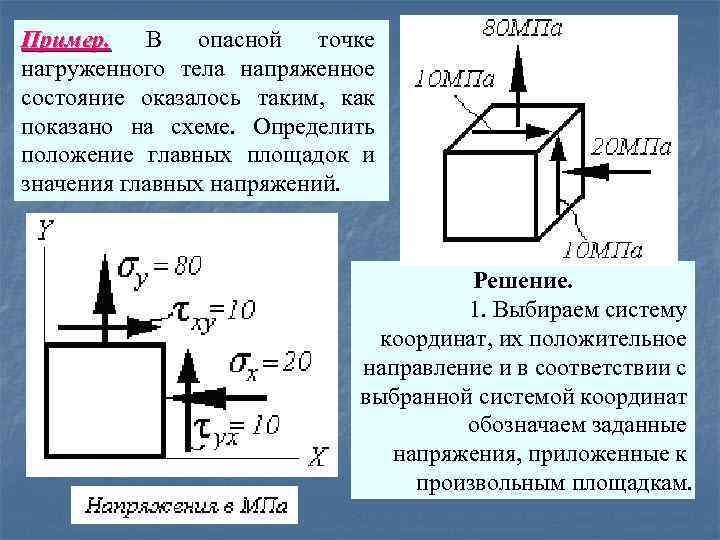 Пример. В опасной точке нагруженного тела напряженное состояние оказалось таким, как показано на схеме. Определить положение главных площадок и значения главных напряжений. Решение. 1. Выбираем систему координат, их положительное направление и в соответствии с выбранной системой координат обозначаем заданные напряжения, приложенные к произвольным площадкам.
Пример. В опасной точке нагруженного тела напряженное состояние оказалось таким, как показано на схеме. Определить положение главных площадок и значения главных напряжений. Решение. 1. Выбираем систему координат, их положительное направление и в соответствии с выбранной системой координат обозначаем заданные напряжения, приложенные к произвольным площадкам.
 2. Определим значения главных напряжений: 3. Обозначим главные напряжения в соответствии с принятым правилом – соответственно: σ1=30+51=81 МПа, σ2=0, σ3=30 -51=-21 МПа. Это есть плоское напряженное состояние. 4. Найдем угол, на который необходимо повернуть произвольные площадки, чтобы получить главные площадки:
2. Определим значения главных напряжений: 3. Обозначим главные напряжения в соответствии с принятым правилом – соответственно: σ1=30+51=81 МПа, σ2=0, σ3=30 -51=-21 МПа. Это есть плоское напряженное состояние. 4. Найдем угол, на который необходимо повернуть произвольные площадки, чтобы получить главные площадки:
 Тогда arctg 2α 0=-11, 30, а α 0=-5, 650. Минус указывает на то, что отсчет угла – по часовой стрелке. 5. Покажем положение главных площадок и вектора главных напряжений. 6. Проверяем правильность решения: а) сумма напряжений – величина постоянная; б) направление поворота произвольных площадок: для получения положения главных площадок произвольную площадку, по которой приложено максимальное нормальное напряжение, необходимо повернуть по направлению приложенного к ней касательного напряжения.
Тогда arctg 2α 0=-11, 30, а α 0=-5, 650. Минус указывает на то, что отсчет угла – по часовой стрелке. 5. Покажем положение главных площадок и вектора главных напряжений. 6. Проверяем правильность решения: а) сумма напряжений – величина постоянная; б) направление поворота произвольных площадок: для получения положения главных площадок произвольную площадку, по которой приложено максимальное нормальное напряжение, необходимо повернуть по направлению приложенного к ней касательного напряжения.
 В данном примере: σ1 + σ 3= σ x + σ y 81 -21=80 -20. По площадке, где приложено максимальное напряжение σy=80 МПа, действует касательное напряжение τxy=10 МПа. Это напряжение поворачивает указанную площадку по ходу часовой стрелки (при взгляде изнутри элемента). Следовательно, эту произвольную площадку необходимо повернуть также по часовой стрелке и получить положение главной площадки, что соответствует решению.
В данном примере: σ1 + σ 3= σ x + σ y 81 -21=80 -20. По площадке, где приложено максимальное напряжение σy=80 МПа, действует касательное напряжение τxy=10 МПа. Это напряжение поворачивает указанную площадку по ходу часовой стрелки (при взгляде изнутри элемента). Следовательно, эту произвольную площадку необходимо повернуть также по часовой стрелке и получить положение главной площадки, что соответствует решению.
 6. 2. Основы теории деформированного состояния Рассматривая понятия о перемещениях и деформациях, мы установили, что компонентами деформаций являются относительные линейные и относительные угловые (углы сдвига) деформации. По аналогии с напряжениями, в теории упругости рассматривают также главные оси деформаций (по направлению которых отсутствуют угловые деформации) и главные деформации. Обозначение их также аналогично обозначениям главных напряжений, т. е. ε 1, ε 2, ε 3.
6. 2. Основы теории деформированного состояния Рассматривая понятия о перемещениях и деформациях, мы установили, что компонентами деформаций являются относительные линейные и относительные угловые (углы сдвига) деформации. По аналогии с напряжениями, в теории упругости рассматривают также главные оси деформаций (по направлению которых отсутствуют угловые деформации) и главные деформации. Обозначение их также аналогично обозначениям главных напряжений, т. е. ε 1, ε 2, ε 3.
 6. 2. 1. Обобщенный закон Гука для изотропного тела Выделим вокруг напряженной точки прямоугольный параллелепипед с длиной ребер, равной единице. Пусть, кроме того, грани параллелепипеда являются главными площадками. Под действием σ1, σ2, σ3 эти грани будут испытывать деформации по всем трем направлениям (по направлениям главных напряжений).
6. 2. 1. Обобщенный закон Гука для изотропного тела Выделим вокруг напряженной точки прямоугольный параллелепипед с длиной ребер, равной единице. Пусть, кроме того, грани параллелепипеда являются главными площадками. Под действием σ1, σ2, σ3 эти грани будут испытывать деформации по всем трем направлениям (по направлениям главных напряжений).
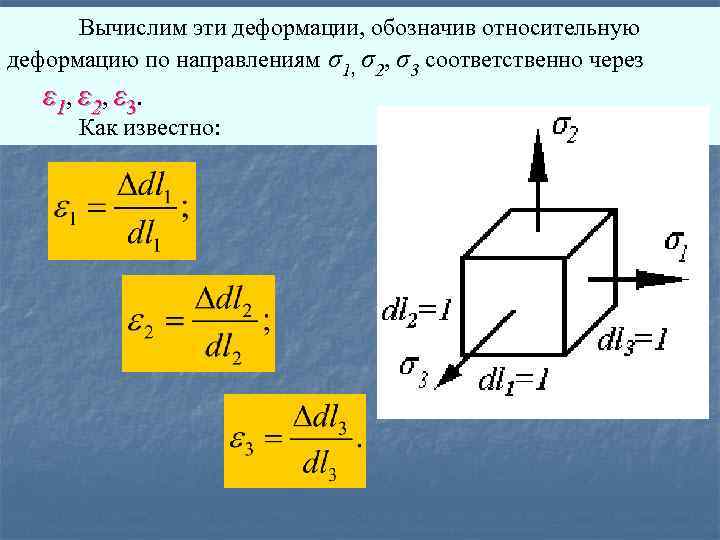 Вычислим эти деформации, обозначив относительную деформацию по направлениям σ1, σ2, σ3 соответственно через ε 1, ε 2, ε 3. Как известно:
Вычислим эти деформации, обозначив относительную деформацию по направлениям σ1, σ2, σ3 соответственно через ε 1, ε 2, ε 3. Как известно:
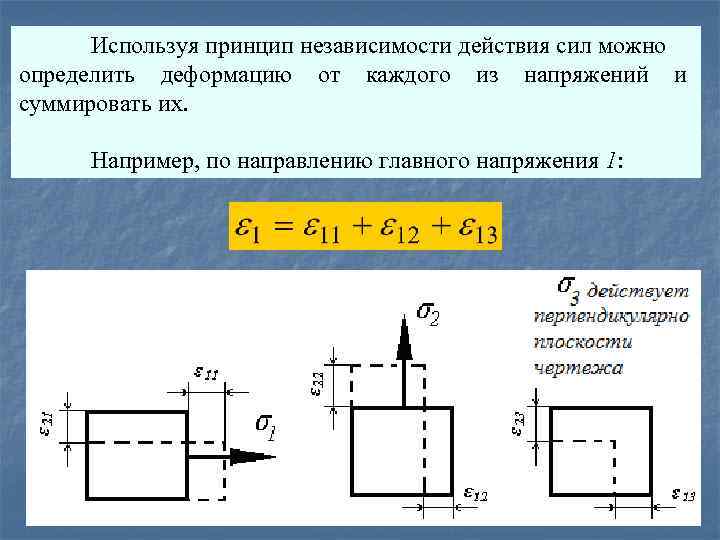 Используя принцип независимости действия сил можно определить деформацию от каждого из напряжений и суммировать их. Например, по направлению главного напряжения 1:
Используя принцип независимости действия сил можно определить деформацию от каждого из напряжений и суммировать их. Например, по направлению главного напряжения 1:
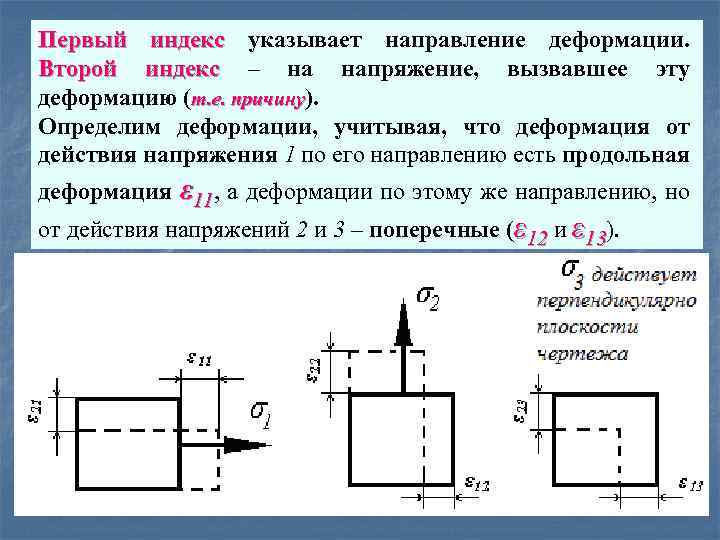 Первый индекс указывает направление деформации. Второй индекс – на напряжение, вызвавшее эту деформацию (т. е. причину). Определим деформации, учитывая, что деформация от действия напряжения 1 по его направлению есть продольная деформация ε 11, а деформации по этому же направлению, но от действия напряжений 2 и 3 – поперечные (ε 12 и ε 13).
Первый индекс указывает направление деформации. Второй индекс – на напряжение, вызвавшее эту деформацию (т. е. причину). Определим деформации, учитывая, что деформация от действия напряжения 1 по его направлению есть продольная деформация ε 11, а деформации по этому же направлению, но от действия напряжений 2 и 3 – поперечные (ε 12 и ε 13).
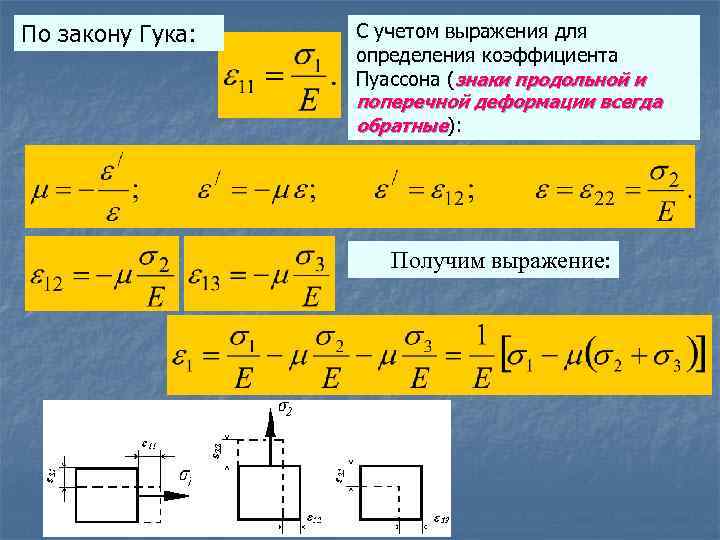 По закону Гука: С учетом выражения для определения коэффициента Пуассона (знаки продольной и поперечной деформации всегда обратные): Получим выражение:
По закону Гука: С учетом выражения для определения коэффициента Пуассона (знаки продольной и поперечной деформации всегда обратные): Получим выражение:
 Выполнив аналогичные операции для деформаций по направлениям напряжений 2 и 3, получим три уравнения, которые носят название обобщенный закон Гука:
Выполнив аналогичные операции для деформаций по направлениям напряжений 2 и 3, получим три уравнения, которые носят название обобщенный закон Гука:
 Легко видеть, что равенство нулю одного из напряжений не означает равенства нулю деформации по этому направлению. Известно, что касательные напряжения не влияют на величину относительных линейных деформаций. Поэтому эти деформации по направлениям и от действия нормальных напряжений, действующих по площадкам общего положения (произвольным площадкам), будут определяться по формулам:
Легко видеть, что равенство нулю одного из напряжений не означает равенства нулю деформации по этому направлению. Известно, что касательные напряжения не влияют на величину относительных линейных деформаций. Поэтому эти деформации по направлениям и от действия нормальных напряжений, действующих по площадкам общего положения (произвольным площадкам), будут определяться по формулам:
 6. 2. 2. Относительное изменение объема Под действием внешних сил упругое тело деформируется, объем его изменяется и в нем накапливается потенциальная энергия. В процессе нагружения тела потенциальная энергия проявляется в виде работы, совершаемой внутренними силами. В общем случае, когда напряженное состояние в различных точках различно, для определения потенциальной энергии деформации необходимо знать изменение объема и количество энергии в каждой элементарной частице тела. Особенно это важно при рассмотрении процесса развития трещин, при решении контактных задач и т. п. Отношение приращения объема элементарного параллелепипеда к его исходному объему называется относительным изменением объема этого параллелепипеда:
6. 2. 2. Относительное изменение объема Под действием внешних сил упругое тело деформируется, объем его изменяется и в нем накапливается потенциальная энергия. В процессе нагружения тела потенциальная энергия проявляется в виде работы, совершаемой внутренними силами. В общем случае, когда напряженное состояние в различных точках различно, для определения потенциальной энергии деформации необходимо знать изменение объема и количество энергии в каждой элементарной частице тела. Особенно это важно при рассмотрении процесса развития трещин, при решении контактных задач и т. п. Отношение приращения объема элементарного параллелепипеда к его исходному объему называется относительным изменением объема этого параллелепипеда:
 Рассмотрим элементарный параллелепипед, но уже с произвольной элементарной длиной ребер dl 1, dl 2, dl 3. Первоначальный объем его определится произведением длин ребер: После нагружения длина ребер изменится и они получат соответствующие абсолютные деформации. Конечная длина ребер равна, соответственно:
Рассмотрим элементарный параллелепипед, но уже с произвольной элементарной длиной ребер dl 1, dl 2, dl 3. Первоначальный объем его определится произведением длин ребер: После нагружения длина ребер изменится и они получат соответствующие абсолютные деформации. Конечная длина ребер равна, соответственно:
 Объем параллелепипеда после деформации получим, перемножив конечные длины граней: Величины относительных деформаций ε 1 , ε 2, ε 3 весьма малы (в упругой области), поэтому их произведениями можно пренебречь. Тогда из последнего выражения: Поделим правую и левую полученного уравнения на d. V: части Используя понятие относительного изменения объема, получим формулу:
Объем параллелепипеда после деформации получим, перемножив конечные длины граней: Величины относительных деформаций ε 1 , ε 2, ε 3 весьма малы (в упругой области), поэтому их произведениями можно пренебречь. Тогда из последнего выражения: Поделим правую и левую полученного уравнения на d. V: части Используя понятие относительного изменения объема, получим формулу:
 Относительное изменение объема тела равно сумме относительных деформаций. Относительное изменение объема есть величина безразмерная. Объем тела не изменяется, если сумма относительных деформаций равна нулю. Подставим в ɛV значения ε 1, ε 2, ε 3 из обобщенного закона Гука:
Относительное изменение объема тела равно сумме относительных деформаций. Относительное изменение объема есть величина безразмерная. Объем тела не изменяется, если сумма относительных деформаций равна нулю. Подставим в ɛV значения ε 1, ε 2, ε 3 из обобщенного закона Гука:
 Выразим ɛV через напряжения по произвольным площадкам: Приведем несколько следствий из последней формулы: 1. Объем тела не изменится, если сумма нормальных напряжений равна нулю. 2. Сумма нормальных напряжений есть величина постоянная:
Выразим ɛV через напряжения по произвольным площадкам: Приведем несколько следствий из последней формулы: 1. Объем тела не изменится, если сумма нормальных напряжений равна нулю. 2. Сумма нормальных напряжений есть величина постоянная:
 3. При всестороннем сжатии (гидростатическом сжатии) сжатии материала нормальные напряжения равны по величине: В этом случае относительное изменение объема окажется равным Откуда следует, что должно выполняться условие μ ≤ 0, 5 (т. к. в случае μ > 0, 5 объем тела должен увеличиваться, что противоречит природе вещей). 4. При μ = 0, 5 объем тела изменяться не будет (εv=0).
3. При всестороннем сжатии (гидростатическом сжатии) сжатии материала нормальные напряжения равны по величине: В этом случае относительное изменение объема окажется равным Откуда следует, что должно выполняться условие μ ≤ 0, 5 (т. к. в случае μ > 0, 5 объем тела должен увеличиваться, что противоречит природе вещей). 4. При μ = 0, 5 объем тела изменяться не будет (εv=0).
 6. 2. 3. Потенциальная энергия деформации Вернемся к рассмотрению параллелепипеда с ребрами элементарно малой длины. На основании закона сохранения энергии потенциальная энергия деформации элементарного параллелепипеда d. U равна работе внешних сил d. W, приложенных к его граням: d. U = d. W. Таким образом, для решения поставленной задачи необходимо определить работу. Предполагается, что все внешние силы действуют одновременно и прикладываются статически, деформации упругие, потерями энергии пренебрегаем.
6. 2. 3. Потенциальная энергия деформации Вернемся к рассмотрению параллелепипеда с ребрами элементарно малой длины. На основании закона сохранения энергии потенциальная энергия деформации элементарного параллелепипеда d. U равна работе внешних сил d. W, приложенных к его граням: d. U = d. W. Таким образом, для решения поставленной задачи необходимо определить работу. Предполагается, что все внешние силы действуют одновременно и прикладываются статически, деформации упругие, потерями энергии пренебрегаем.
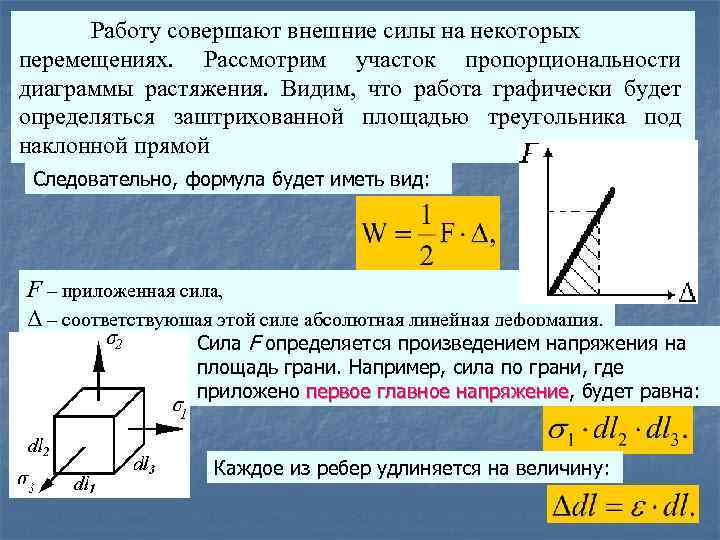 Работу совершают внешние силы на некоторых перемещениях. Рассмотрим участок пропорциональности диаграммы растяжения. Видим, что работа графически будет определяться заштрихованной площадью треугольника под наклонной прямой Следовательно, формула будет иметь вид: F – приложенная сила, Δ – соответствующая этой силе абсолютная линейная деформация. Сила F определяется произведением напряжения на площадь грани. Например, сила по грани, где приложено первое главное напряжение, будет равна: напряжение Каждое из ребер удлиняется на величину:
Работу совершают внешние силы на некоторых перемещениях. Рассмотрим участок пропорциональности диаграммы растяжения. Видим, что работа графически будет определяться заштрихованной площадью треугольника под наклонной прямой Следовательно, формула будет иметь вид: F – приложенная сила, Δ – соответствующая этой силе абсолютная линейная деформация. Сила F определяется произведением напряжения на площадь грани. Например, сила по грани, где приложено первое главное напряжение, будет равна: напряжение Каждое из ребер удлиняется на величину:
 Тогда работа d. W внешних сил на этих удлинениях и равная ей потенциальная энергия d. U элементарного параллелепипеда: Полная удельная потенциальная энергия деформации определяется отношением
Тогда работа d. W внешних сил на этих удлинениях и равная ей потенциальная энергия d. U элементарного параллелепипеда: Полная удельная потенциальная энергия деформации определяется отношением
 Тогда Если в записанной формуле относительные ε деформации заменить их выражениями из обобщенного закона Гука:
Тогда Если в записанной формуле относительные ε деформации заменить их выражениями из обобщенного закона Гука:
 Получим: Размерность удельной потенциальной энергии Н∙м/м 3 или Н/м 2, т. е. размерность напряжений. Под действием внешних сил изменяется не только объем параллелепипеда, но и его форма. Таким образом, полная удельная потенциальная энергия может быть определена двумя составляющими – удельной потенциальной энергией изменения объема uоб и удельной потенциальной энергией изменения формы uф.
Получим: Размерность удельной потенциальной энергии Н∙м/м 3 или Н/м 2, т. е. размерность напряжений. Под действием внешних сил изменяется не только объем параллелепипеда, но и его форма. Таким образом, полная удельная потенциальная энергия может быть определена двумя составляющими – удельной потенциальной энергией изменения объема uоб и удельной потенциальной энергией изменения формы uф.
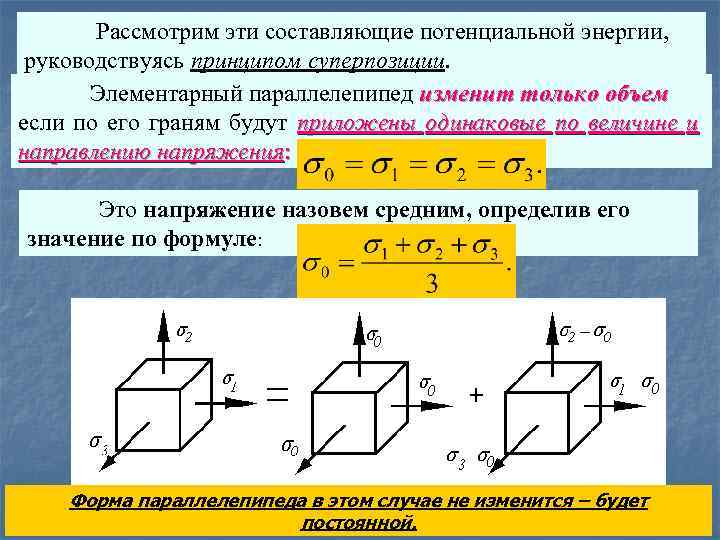 Рассмотрим эти составляющие потенциальной энергии, руководствуясь принципом суперпозиции. Элементарный параллелепипед изменит только объем если по его граням будут приложены одинаковые по величине и направлению напряжения: Это напряжение назовем средним, определив его значение по формуле: Форма параллелепипеда в этом случае не изменится – будет постоянной.
Рассмотрим эти составляющие потенциальной энергии, руководствуясь принципом суперпозиции. Элементарный параллелепипед изменит только объем если по его граням будут приложены одинаковые по величине и направлению напряжения: Это напряжение назовем средним, определив его значение по формуле: Форма параллелепипеда в этом случае не изменится – будет постоянной.
 Разность напряжений (соответствующих главных и среднего), приложенных к граням, вызовет только изменение формы параллелепипеда. (объем тела не изменяется, если сумма нормальных напряжений равна нулю). Сумма приложенных к граням напряжений равна:
Разность напряжений (соответствующих главных и среднего), приложенных к граням, вызовет только изменение формы параллелепипеда. (объем тела не изменяется, если сумма нормальных напряжений равна нулю). Сумма приложенных к граням напряжений равна:
 Исследуемые напряженные состояния описываются соответствующими тензорами: Tσ – исследуемый тензор напряженного состояния, T 0 – шаровой тензор, тензор Dσ – девиатор напряжений (итальянск. – de via – отклонение от дороги или направления).
Исследуемые напряженные состояния описываются соответствующими тензорами: Tσ – исследуемый тензор напряженного состояния, T 0 – шаровой тензор, тензор Dσ – девиатор напряжений (итальянск. – de via – отклонение от дороги или направления).
 А). Выражение для удельной потенциальной энергии изменения объема: σ1 , σ2 , σ3 среднее напряжение σ0 : подставим вместо главных напряжений Или для напряжений по произвольным площадкам:
А). Выражение для удельной потенциальной энергии изменения объема: σ1 , σ2 , σ3 среднее напряжение σ0 : подставим вместо главных напряжений Или для напряжений по произвольным площадкам:
 Б). Выражение для удельной потенциальной энергии изменения формы: подставим вместо главных напряжений σ1 , σ2 , σ3 разность этих напряжений и среднего напряжения σ0 : Для единообразия, последнюю формулу запишем в виде:
Б). Выражение для удельной потенциальной энергии изменения формы: подставим вместо главных напряжений σ1 , σ2 , σ3 разность этих напряжений и среднего напряжения σ0 : Для единообразия, последнюю формулу запишем в виде:
 Эта же энергия может быть определена и через напряжения, действующие по произвольным площадкам: G - модуль упругости II рода (модуль сдвига).
Эта же энергия может быть определена и через напряжения, действующие по произвольным площадкам: G - модуль упругости II рода (модуль сдвига).


