6 7 Day 1 Applying Simple and Compound

6. 7 Day 1 Applying Simple and Compound Interest p 303 Warm Up Find each % of increase or decrease. 1. from 40 to 59 2. from 85 to 170 * NS 1. 7 Solve problems that involve discounts, markups, commissions, and profit and compute simple and compound interest. LO: I will use multiplication strategies to evaluate simple interest. TIPS: (Simple) I = P r t P + I = A (Amount Total)

• When you deposit money into a bank, the bank pays you interest. • When you borrow money from a bank, you pay interest to the bank. Simple interest is money paid only on the principal. Rate of interest is the percent charged or earned. I=P rt Principal is the amount of money borrowed or invested. Time that the money is borrowed or invested (in years).

Finding Interest and Total Payment on a Loan- To buy a car, Jessica borrowed $15, 000 for 3 years at an annual simple interest rate of 9%. How much interest will she pay if she pays the entire loan off at the end of the third year? What is the total amount that she will repay? I=P r t Use the formula. First, find the interest she will pay. I = ______ I = _____ __ Substitute. ____ for 9%. Principal + Interest = Amount Total _____ + _____ = _______ Jessica will repay a total of $_____ on her loan. Determining the Amount of Investment Time- Nancy invested $6000 in a bond at a yearly rate of 3%. She earned $450 in interest. How long was the money invested? I=Prt _____= _____ = ____t Use the formula. _____ t Substitute values The money was invested for ______years, or ____ years and ____ months.

Computing Total Savings- John’s parents deposited $1000 into a savings account as a college fund when he was born. How much will John have in this account after 18 years at a yearly simple interest rate of 4%? I = ____ The interest is $____. Now find the total. P+I=A ______ + _______ = A John will have $_____ in the account after 18 years. ______ = A Finding the Rate of Interest- Mr. Twain borrowed $8000 for 4 years to make home improvements. If he repaid a total of $10, 320, at what interest rate P + I = A (Amount Total) did he borrow the money? _____ + I = _______ He paid $___ in interest. Now use the amount of interest paid to find the interest ______ (%). I=Prt ______= ______ r _______= _______ r Divide both sides by 32, 000. Mr. Twain borrowed the money at an annual rate of _____ or ___%. 6. 7 RM & SRe p 307

6. 7 Day 2 Compound Interest p 303 LO: I will evaluate compound interest using (Simple) I = P r t “and a little more. ” Compound interest is INTEREST PAID on the PRINCIPAL, and ALSO on the INTEREST. A = final dollar value P = principal r = rate of interest nt A = P(1 + r ) n t = time in years n = number of compounding periods per year.

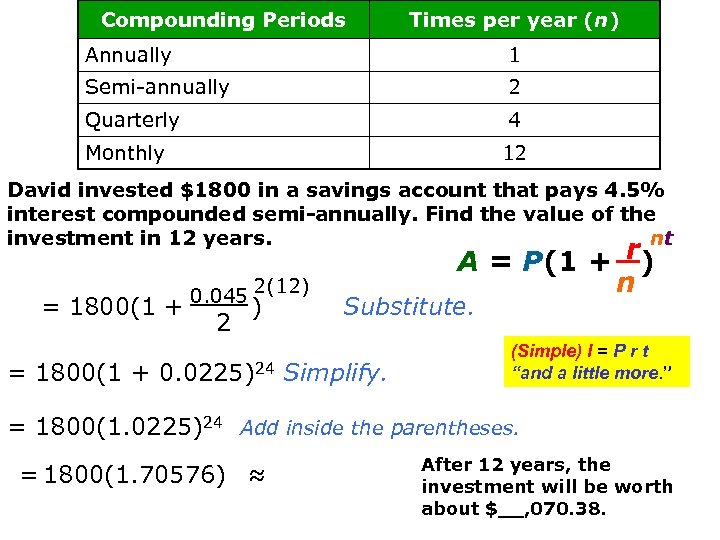Compounding Periods Times per year (n) Annually 1 Semi-annually 2 Quarterly 4 Monthly 12 David invested $1800 in a savings account that pays 4. 5% interest compounded semi-annually. Find the value of the nt investment in 12 years. = 1800(1 + 0. 045 2(12) t 2 ) A = P(1 + r) n Substitute. = 1800(1 + 0. 0225)24 Simplify. (Simple) I = P r t “and a little more. ” = 1800(1. 0225)24 Add inside the parentheses. = 1800(1. 70576) ≈ After 12 years, the investment will be worth about $__, 070. 38.

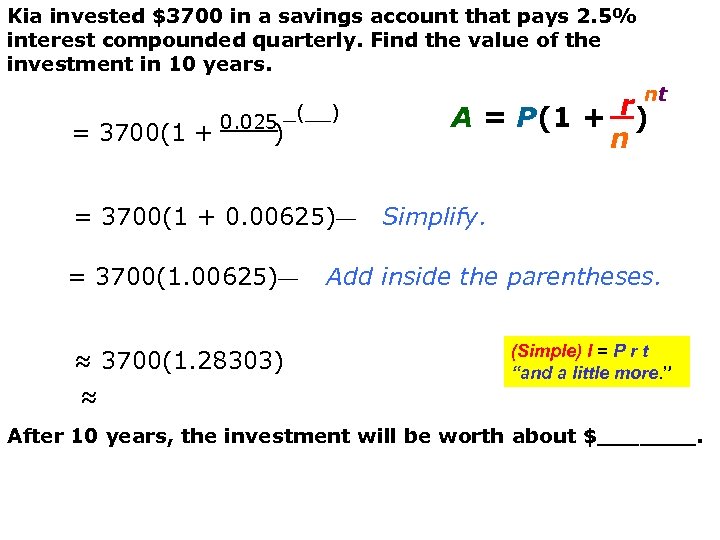Kia invested $3700 in a savings account that pays 2. 5% interest compounded quarterly. Find the value of the investment in 10 years. = 3700(1 + 0. 025 _(__) t ) = 3700(1 + 0. 00625)__ = 3700(1. 00625)__ ≈ 3700(1. 28303) ≈ nt r) A = P(1 + n Simplify. Add inside the parentheses. (Simple) I = P r t “and a little more. ” After 10 years, the investment will be worth about $_______.

The Hemmings borrowed $3000 for home improvements. They repaid the loan and $600 in simple interest four years later. What simple annual interest rate did they pay? (Simple) I = P r t “and a little more. ” Theresa invested $800 in a savings account that pays 4% interest compounded quarterly. Find the value of the investment after 6 years. nt A = P(1 + r) n (Simple) I = P r t “and a little more. ” RTGO? Quiz Page 308 all