5 Решение задачи Коши Алгоритмы численного решения задачи

5 Решение задачи Коши Алгоритмы численного решения задачи Коши. Запись алгоритма метода Рунге-Кутта 4 -го порядка (метода Рунге-Кутта 3 -го порядка, неявного метода Эйлера – на выбор) в виде блок-схемы и на одном из языков программирования.

Задача Коши Пусть решается уравнение вида y ` = f(x, y) (1) с начальным условием y(x 0) = y 0 (2). Будем считать, что функция f(x, y) такова, что у задачи (1) – (2) имеется единственное решение.

Численное решение задачи состоит в построении таблицы приближенных значений y 1, y 2, …, yn решения уравнения y(x) в точках x 1, x 2, …, xn. Чаще всего xi = x 0 + i h, i = 1, 2, …, n. Точки xi называются узлами сетки, а величина h – шагом (h > 0).

Метод Эйлера является простейшим численным методом для решения задачи Коши. Допустим, что в некоторой точке xi нам известно значение y. y(xi) – точное значение, yэi – приближенное(~Эйлера). Рассмотрим разложение функции y(x) в ряд Тейлора в окрестности точки xi, отбросив все члены, содержащие производные второго порядка и выше: y(xi+1) = y(xi) + h·y ` (xi) + O(h 2) yi+1 = y(xi) + h · f(xi, y(xi)) + O(h 2) x 0 – задано. А для всех i = 0, 1, …, yi+1 = yi + h · f(xi, yi) (5). В результате получаем сеточную функцию. Если требуется аналитически представить решение, то необходимо каким – либо образом по полученной таблице построить формулу (интерполяция, метод наименьших квадратов, …).

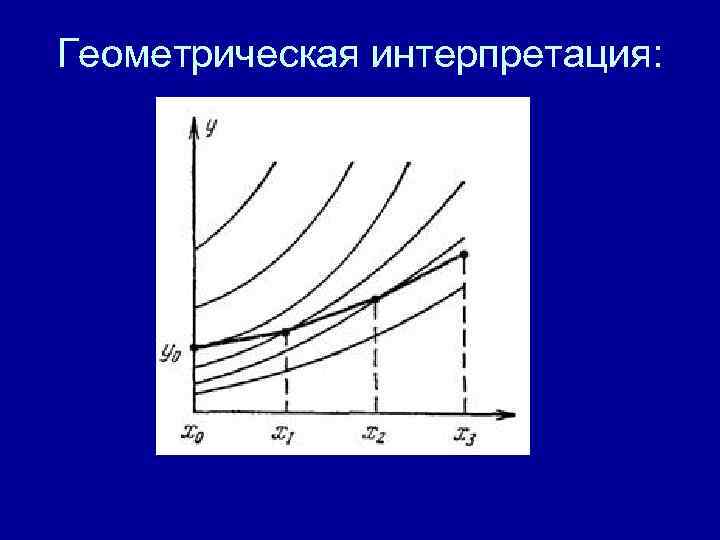Геометрическая интерпретация:

Отбрасывая все члены порядка выше первого, получаем уравнение касательной. y 1 = y 0 + y ` (x 0) · (x 1 – x 0) + o(h 2) Вычисляя значение в точке x 1, переходим к новой интегральной кривой. Таким образом, шаг за шагом все более удаляемся от искомой интегральной кривой. Причем больше шаг, тем больше допускаемая погрешность. Погрешность каждого шага метода составляет величину h 2. На каждом шаге метода существует также начальная погрешность. εih – погрешность одного шага (от xi к xi+1) εi 0 – начальная погрешность i-ого шага

Рассмотрим погрешность εn, которая накапливается при вычислении n-ого значения. εn = εn 0 + εnh = εn-10 + εn-1 h + εnh =. . . = ε 10 + ε 1 h + ε 2 h +. . . + εnh = ε 10 + n ∙ o(h 2) = ε 10 – начальная погрешность(с которой задано y 0 в (2)) = ε 0` + o(h 2) = o(h) Метод Эйлера – метод первого порядка.

Метод Эйлера относится к группе одношаговых методов, в которых для расчёта новой точки требуется информация только о последней вычисленной точке. Если расчётные формулы численного метода согласуются с разложением в ряд Тейлора до членов порядка hp, то число p называют порядком метода. Метод Эйлера – метод первого порядка. Не путать с погрешностью метода - O(h 2) !

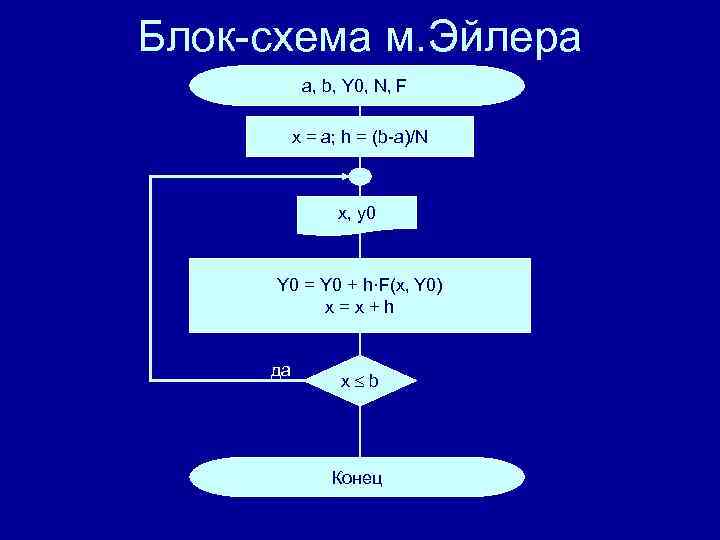Блок-схема м. Эйлера a, b, Y 0, N, F x = a; h = (b-a)/N x, y 0 Y 0 = Y 0 + h·F(x, Y 0) x = x + h да x b Конец

Реализация м. Эйлера PROGRAM Resh_ODY; {Решение ОДУ методом Эйлера} uses CRT; {Тест: y'=2*e^(-x)*Cos(2*x)-y; y(0)=0} Type Funcx=function(x: real): real; Funcxy=function(x, y: real): real; Function f 1(x: real): real; far; Begin f 1: =exp(-x)*Sin(2*x); {Точное решение: y=e^(-x)*Sin(2*x)} End; Function f 2(x, y: real): real; far; Begin f 2: =2*exp(-x)*Cos(2*x)-y; End;

Реализация м. Эйлера [a, b] Procedure Eyler(F 1: Funcx; F 2: Funcxy; a, b, eps, y 0: real; n: integer); {F 1 -точное; F 2 -правая часть уравнения} Var yi 0, yii: real; e, h, xk, yk, fk: real; k, l: integer; fl: boolean; Begin h: =(b-a)/n; xk: =a; yk: =y 0; writeln(xk: 8: 4, yk: 8: 4, f 1(xk): 8: 4, abs(yk-f 1(xk)): 12); for k: =1 to n do Begin Fk: =f 2(xk, yk); yi 0: =yk+h*Fk; fl: =false; { У Т О Ч Н Е Н И Е } l: =0; repeat yii: =yk+h*(Fk+f 2(xk+h, yi 0))/2; e: =ABS((yii-yi 0)/yii); yi 0: =yii; If e

Уточнение? Модификация метода – более точный переход в новую точку. Геометрически это означает, что определяется направление интегральной кривой в исходной точке и во вспомогательной, а в качестве окончательного берётся среднее этих направлений. Процесс повторяется до нужной точности. { У Т О Ч Н Е Н И Е } l: =0; repeat yii: =yk+h*(Fk+f 2(xk+h, yi 0))/2; e: =ABS((yii-yi 0)/yii); yi 0: =yii; If e

Метод Рунге-Кутта решения дифференциальных уравнений и их систем

Методом Рунге-Кутта в литературе обычно называется одношаговый метод четвёртого порядка. Одно дифференциальное уравнение – частный случай системы с одним элементом. Поэтому, далее речь пойдет для определенности о системе уравнений. Метод может быть полезен и для решения дифференциальных уравнений высшего (второго и т. д. ) порядка, т. к. они могут быть представлены системой дифференциальных уравнений первого порядка.

Метод позволяет решать системы обыкновенных дифференциальных уравнений (ОДУ) первого порядка следующего вида: и т. д. , которые имеют решение: и т. д. , где t – независимая переменная (например, время); X, Y и т. д. – искомые функции (зависимые от t переменные). Функции f, g и т. д. – заданы. Также предполагаются заданными и начальные условия, т. е. значения искомых функций в начальный момент.

Метод Рунге-Кутта заключается в рекуррентном применении следующих формул: … где

Точность метода Погрешность метода на одном шаге сетки M h 5. При оценке используют правило Рунге (двойной пересчёт). Справедлива оценка

Блок-схема метода Р-К_IV x 0, Y 0, h, N < ЦИКЛ: I = 1, N> Fk = f 2(x 0, y 0) K 1 = h·Fk Y 0 = Y 0 +(K 1+2 K 2+2 K 3+K 4)/6 x 0 = x 0 + h K 2 = h·f 2(x 0+h/2, Y 0+k 1/2) x 0, Y 0 K 3 = h·f 2(x 0+h/2, Y 0+k 2/2) K 4 =h·f 2(x 0+h/2, Y 0+k 3) < КОНЕЦ ЦИКЛА > Конец

Реализация м. Р-К Procedure Runge_Kutta 4(F 1: Funcx; F 2: Funcxy; a, b, y 0: real; n: integer); Var {F 1 -точное; F 2 -правая часть уравнения} e, h, xk, yk 1, fk: real; {Тест: y'=2*e^(-x)*Cos(2*x)-y; y(0)=0} {Точное решение: y=e^(-x)*Sin(2*x)} k 1, k 2, k 3, k 4: real; i: integer; Begin h: =(b-a)/n; xk: =a; yk: =y 0; writeln(xk: 8: 4, yk: 8: 4, f 1(xk): 8: 4, abs(yk-f 1(xk)): 12); for i: =1 to n do Begin Fk: =f 2(xk, yk); k 1: =h*Fk; k 2: =h*f 2(xk+h/2, yk+k 1/2); k 3: =h*f 2(xk+h/2, yk+k 2/2); k 4: =h*f 2(xk+h/2, yk+k 3); yk 1: =yk+(k 1+2*k 2+2*k 3+k 4)/6; xk: =xk+h; yk: =yk 1; writeln(xk: 8: 4, yk: 8: 4, f 1(xk): 8: 4, abs(yk-f 1(xk)): 12); End; END; {Runge_Kutta 4}

Реализация Метода Рунге-Кутта (Delphi) type TVars. Array = array of real; // вектор переменных включая независимую TInit. Array = array of real; // вектор начальных значений TFun. Array = array of function(Vars. Array: TVars. Array ): real; // вектор функций TRes. Array = array of real; // матрица результатов TCoefs. Array = array of real; // вектор коэффициентов метода function Runge_Kutt( // метод Рунге-Кутта Fun. Array: TFun. Array; // массив функций First: real; // начальная точка по независимой координате Last: real; // конечная точка по независимой координате Steps: Integer; // число шагов по независимой координате Init. Array: TInit. Array; // вектор начальных значений var Res: TRes. Array // матрица результатов включая независ. переменную ): Word; // возвращаемое значение - код ошибки

implementation Function Runge_Kutt( // метод Рунге-Кутта Fun. Array: TFun. Array; // массив функций First: Extended; // начальная точка по независимой координате Last: Extended; // конечная точка по независимой координате Steps: Integer; // число шагов по независимой координате Init. Array: TInit. Array; // вектор начальных значений var Res: TRes. Array // матрица результатов включая независ. переменную ): Word; // возвращаемое значение - код ошибки var Num: Word; // число уравнений Num. Init: Word; // число начальных условий Delt: real; // шаг разбиения Vars: TVars. Array; // вектор переменных включая независимую Vars 2, Vars 3, Vars 4: TVars. Array; // значения перем. для 2 -4 коэф. Coefs 1: TCoefs. Array; // вектор 1 -ыx коэффициентов в методе Coefs 2: TCoefs. Array; // вектор 2 коэффициентов в методе Coefs 3: TCoefs. Array; // вектор 3 коэффициентов в методе Coefs 4: TCoefs. Array; // вектор 4 коэффициентов в методе I: Integer; // счетчик цикла по итерациям J: Word; // индекс коэф. -тов метода K: Integer; // счетчик прочих циклов

begin Num: =Length(Fun. Array); // узнаем число уравнений Num. Init: =Length(Init. Array); // узнаем число начальных условий If Num. Init<>Num then begin Result: =100; // код ошибки 100: число уравнений не равно числу нач. усл. Exit; end; Delt: =(Last-First)/Steps; // находим величину шага разбиений Set. Length(Res, Num+1, Steps+1); // задаем размер матрицы ответов с незав. перем. Set. Length(Vars, Num+1); // число переменных включая независимую Set. Length(Vars 2, Num+1); // число переменных для 2 -го коэф. включая независимую Set. Length(Vars 3, Num+1); // число переменных для 3 -го коэф. включая независимую Set. Length(Vars 4, Num+1); // число переменных для 4 -го коэф. включая независимую Set. Length(Coefs 1, Num); // число 1 -ыx коэф. метода по числу уравнений Set. Length(Coefs 2, Num); // число 2 -ыx коэф. метода по числу уравнений Set. Length(Coefs 3, Num); // число 3 -иx коэф. метода по числу уравнений Set. Length(Coefs 4, Num); // число 4 -ыx коэф. метода по числу уравнений

// Начальные значения переменных: Vars[0]: =First; For K: =0 to Num. Init-1 do Vars[K+1]: =Init. Array[K]; For J: =0 to Num do Res[J, 0]: =Vars[J]; // первая точка результата For I: =0 to Steps-1 do // начало цикла иттераций begin For J: =0 to Num-1 do Coefs 1[J]: =Fun. Array[J](Vars)*delt; // 1 -й коэфф. // Находим значения переменных для второго коэф. Vars 2[0]: =Vars[0]+delt/2; For K: =1 to Num do Vars 2[K]: =Vars[K]+Coefs 1[K-1]/2; For J: =0 to Num-1 do Coefs 2[J]: =Fun. Array[J](Vars 2)*delt; // 2 -й коэф. // Находим значения переменных для третьго коэф. Vars 3[0]: =Vars[0]+delt/2; For K: =1 to Num do Vars 3[K]: =Vars[K]+Coefs 2[K-1]/2; For J: =0 to Num-1 do Coefs 3[J]: =Fun. Array[J](Vars 3)*delt; // 3 коэфф. // Находим значения переменных для 4 коэф. Vars 4[0]: =Vars[0]+delt; For K: =1 to Num do Vars 4[K]: =Vars[K]+Coefs 3[K-1]; For J: =0 to Num-1 do Coefs 4[J]: =Fun. Array[J](Vars 4)*delt; // 4 коэфф.

// Находим новые значения переменных включая независимую Vars[0]: =Vars[0]+delt; For K: =1 to Num do Vars[K]: =Vars[K]+(1/6)*(Coefs 1[K-1]+2*(Coefs 2[K-1]+Coefs 3[K-1])+Coefs 4[K-1]); // Результат иттерации: For J: =0 to Num do Res[J, I+1]: =Vars[J]; end; // конец итераций Result: =0; // код ошибки; 0 - нет ошибок end; Возвращаемое функцией Runge_Kutt значение – код ошибки. Вы можете дополнить список ошибок по своему усмотрению. Рассчитанные функции системы помещаются в массив Res. Чтобы не загромождать код, в модуле опущены проверки (типа блоков try).

Описание функции Runge_Kutt Function Runge_Kutt (Fun. Array: TFun. Array; First: real; Last: real; Steps: Integer; Init. Array: TInit. Array; var Res: TRes. Array): Word; Здесь: Fun. Array - вектор функций (правых частей уравнений системы); First, Last - начальная и конечная точки расчетного интервала; Steps - число шагов по расчетному интервалу; Init. Array - вектор начальных значений Res - матрица результатов включая независимую переменную.

В модуле описаны типы: type TVars. Array = array of real; // вектор переменных включая независимую TInit. Array = array of real; // вектор начальных значений TFun. Array = array of function(Vars. Array: TVars. Array ): real; // вектор функций TRes. Array = array of real; // матрица результатов TCoefs. Array = array of real; // вектор коэффициетов метода Функция возвращает коды ошибок: 0 – нет ошибок; 100 - число уравнений не равно числу начальных условий.

Решение содержится в переменной-матрице Res. Первый индекс матрицы относится к переменной (0 – независимая переменная, 1 – первая зависимая и т. д. ), второй – к номеру расчетной точки (0 – начальная точка).

Пример использования модуля Создадим новое приложение и подключим к нему модуль. На форме приложения разместим кнопку Button 1 и область текста Memo 1. Нажатие кнопки приведет к расчету точек системы, которые будут выведены в текстовую область. Поместим в приложение две функции и обработчик нажатия кнопки: //Задаем функции (правые части уравнений) function f 0(Var. Array: TVars. Array): real; begin Result: =4*Var. Array[0]*Var. Array[0]; end; function f 1(Var. Array: TVars. Array): real; begin Result: =1; end;

procedure TForm 1. Button 1 Click(Sender: TObject); var I: Integer; Fun. Array: TFun. Array; // массив функций First: real; // начальная точка по независимой координате Last: real; // конечная точка по независимой координате Steps: Integer; // число шагов по независимой координате Init. Array: TInit. Array; // вектор начальных значений Res: TRes. Array; // матрица результатов включая независ. переменную

begin // Создаем вектор функций: Set. Length(Fun. Array, 2); Fun. Array[0]: =f 0; Fun. Array[1]: =f 1; // Задаем интервал и число шагов: First: =0; Last: =10; Steps: =10; // Задаем начальные условия: Set. Length(Init. Array, 2); Init. Array[0]: =0; Init. Array[1]: =0; // Вызов метода и получение результатов: Memo 1. Lines. Clear; I: =Runge_Kutt(Fun. Array, First, Last, Steps, Init. Array, Res); Show. Message('Код ошибки = '+Int. To. Str(I)); For I: =0 to Steps do Memo 1. Lines. Add(floattostr(Res[0, I])+' '+floattostr(Res[1, I])+‘ ‘ +floattostr(Res[2, I])); end;

The End