5 Реактивное движение 2 ЦЕНТP 3 Теоpема ЦЕНТP

5. Реактивное движение. 2 ЦЕНТP 3. Теоpема ЦЕНТP ИНЕPЦИИ 4. ДВИЖЕНИЕ ТЕЛ 2. СИСТЕМЫ ТВЕРДОГО 4. о движении 5. С ПЕРЕМЕННОЙ атериальных точек? 6. МАССОЙ. 5. центpа инеpции.

– это геометрическая точка, характеризующая движение системы частиц как целого.

Положение ЦЕНТРА ИНЕРЦИИ системы материальных точек определяется следующим образом:

где — радиус-вектор центра инерции, — радиус-вектор i-й точки системы. — масса i-й точки. — масса системы.

Выразим импульс системы через скорость движения ее центра масс. получим

Поскольку для замкнутой системы , то и . центр масс замкнутой системы движется прямолинейно и равномерно или остается неподвижным. Следовательно,

РАДИУС-ВЕКТОР центра инерции ТВЕРДОГО ТЕЛА определяется следующим образом

где — радиус-вектор центра инерции, — радиус-вектор элементарного объема тела , — масса тела.

Движение твёрдого тела можно рассматривать как 1. суперпозицию поступательного движения центра масс и вращательного движения тела вокруг его центра масс. 2. Центр масс при этом движется так же, как двигалась бы материальная точка с такой же массой.

Система отсчёта, связанная с центром инерции называется системой центра инерции. 3. Полный импульс замкнутой системы относительно центра инерции всегда остаётся равным нулю, что позволяет упростить уравнения движения.

Рассмотрим свободное движение двух тел с массами m 1 и m 2, связанных друг с другом пружинкой, которую для простоты будем считать невесомой.

Применим второй закон Ньютона к каждой из материальных точек: где – импульс точки 1, – сила, действующая на точку 1 со стороны пружинки. – импульс точки 2, – сила, действующая на точку 2 со стороны пружинки.

Сложим два уравнения движения: Но по III-му закону Ньютона

Поэтому Поменяв местами операции суммирования и дифференцирования, получим

Следовательно, импульс системы двух тел есть величина постоянная Подставим сюда выражение для импульсов частиц, и после следующей цепочки преобразований получим

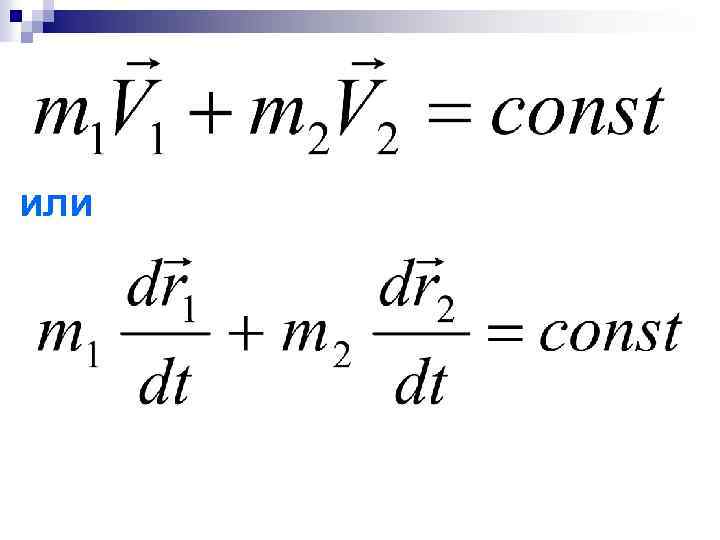или

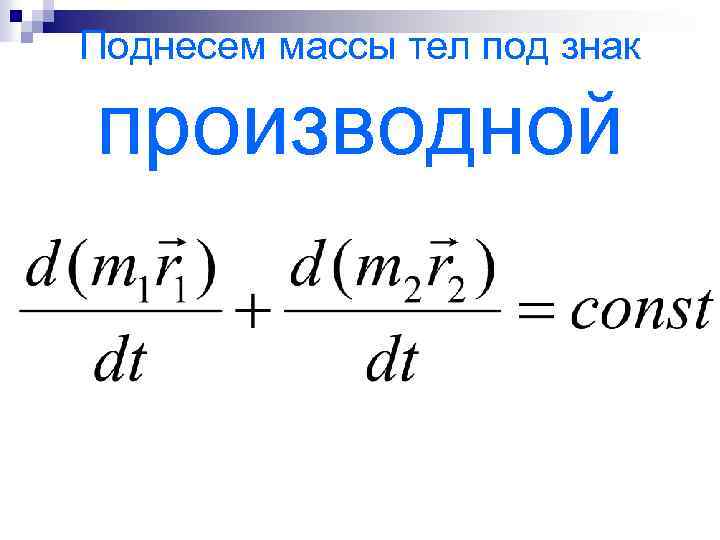Поднесем массы тел под знак производной

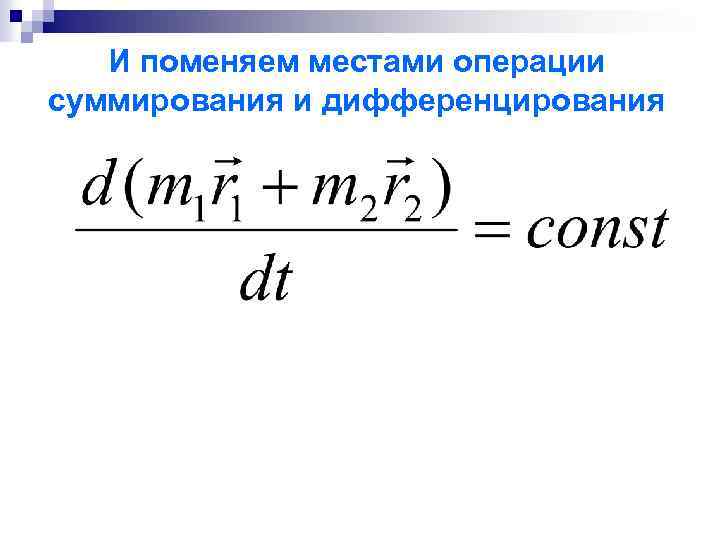И поменяем местами операции суммирования и дифференцирования

Разделив обе части последнего равенства на суммарную массу, m = m 1 + m 2, получаем уравнение

Введем вектор который назовем радиус- вектором инерции центра системы материальных точек

Предыдущее уравнение перепишем в виде где – скорость движения центра инерции системы материальных точек

Таким обpазом, центр инерции замкнутой системы материальных точек движется с постоянной скоростью (независимо от наличия колебательного и вращательного движения материальных точек системы).

ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА ИНЕРЦИИ СИСТЕМЫ центр инерции системы движется как материальная точка, масса которой равна массе всей системы, а действующая сила — геометрической сумме всех внешних сил, действующих на систему.

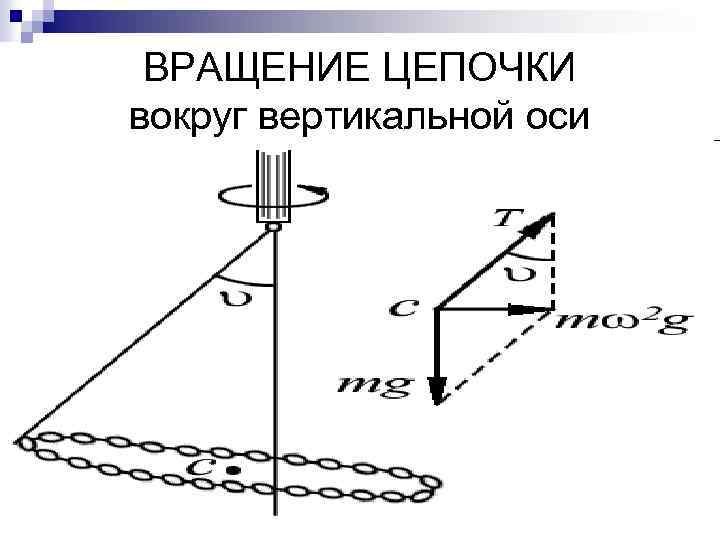ВРАЩЕНИЕ ЦЕПОЧКИ вокруг вертикальной оси

Рассмотрим в качестве примера действие реактивного двигателя.

При сгорании топлива в камере сгорания ракеты образуются газы, нагретые до высокой температуры.

В течение короткого интервала времени t из сопла ракеты выбрасываются со скоростью u относительно ракеты горячие газы массой m.

Ракета и выбрасываемые газы взаимодействуют между собой. На основании закона сохранения импульса при отсутствии внешних сил сумма векторов импульсов взаимодействующих тел остается постоянной.

До начала работы двигателей импульс ракеты и горючего был равен нулю, следовательно, и после включения сумма изменений векторов импульса ракеты и импульса истекающих газов равна нулю:

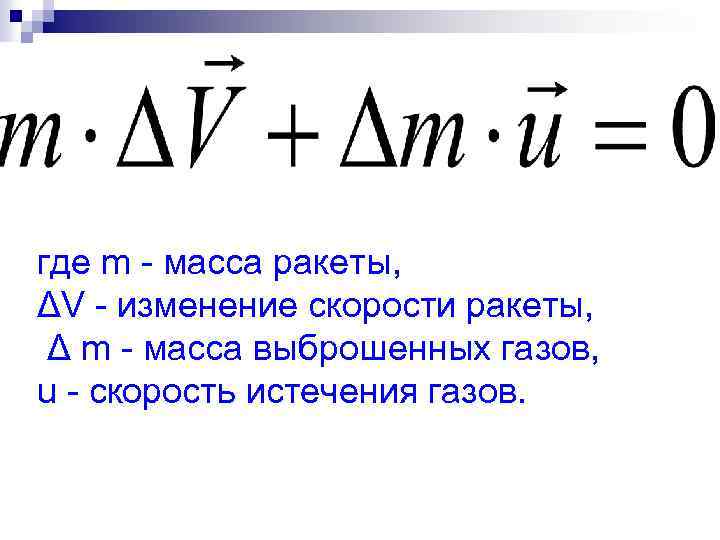где m - масса ракеты, ΔV - изменение скорости ракеты, Δ m - масса выброшенных газов, u - скорость истечения газов.

Отсюда для векторов импульса получаем: Разделим обе части равенства на интервал времени Δt, в течение которого работали двигатели ракеты:

Если же на ракету действует внешняя сила F, то получим

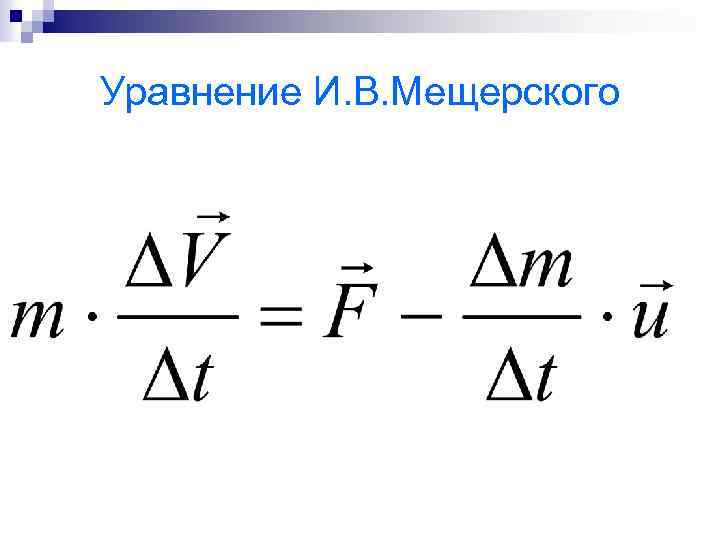Уравнение И. В. Мещерского

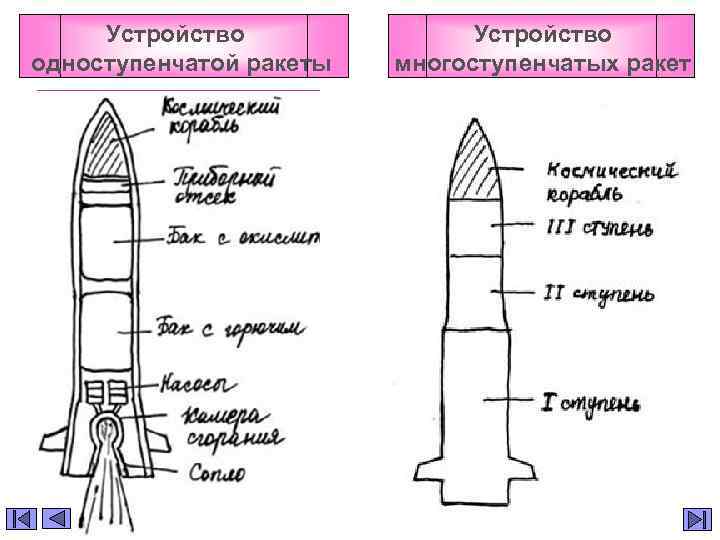Устройство одноступенчатой ракеты Устройство многоступенчатых ракет

Шар Герона Герон Александрийский – греческий механик и математик. Одно из его изобретений носит название Шар Герона. В шар наливалась вода, которая нагревалась огнем. Вырывающийся из трубки пар вращал этот шар. Эта установка иллюстрирует реактивное движение.

Примеры реактивного движения можно найти в природе. Таким образом передвигаются некоторые морские животные: кальмары и медузы. Человек стал использовать такой способ передвижения только в XX веке.

Кибальчич Н. А. Циолковский К. Э Королев С. П.