5 Моменты случайной величины коэффициент

5. Моменты случайной величины •

коэффициент асимметрии . Если А>0, то кривая распределения более полога справа от моды Если А<0, то кривая распределения более полога слева от моды. Для нормального закона распределения А=0. μ 4 – характеристика крутости (островершинности или плосковершинности) распределения. - коэф-т эксцесса. Для нормального распределения Е=0. Если некоторое распределение имеет Е≠ 0, то кривая этого распределения отличается от нормальной кривой. Если E>0, то кривая имеет более высокую и острую вершину, чем нормальная кривая. Если E<0, то сравниваемая кривая имеет более низкую и плоскую вершину, чем норм. кривая. При этом, нормальное и сравниваемое с ним распределение имеют одинаковые м. о. и дисперсии.

Распределение функций нормальных с. в. •

. .

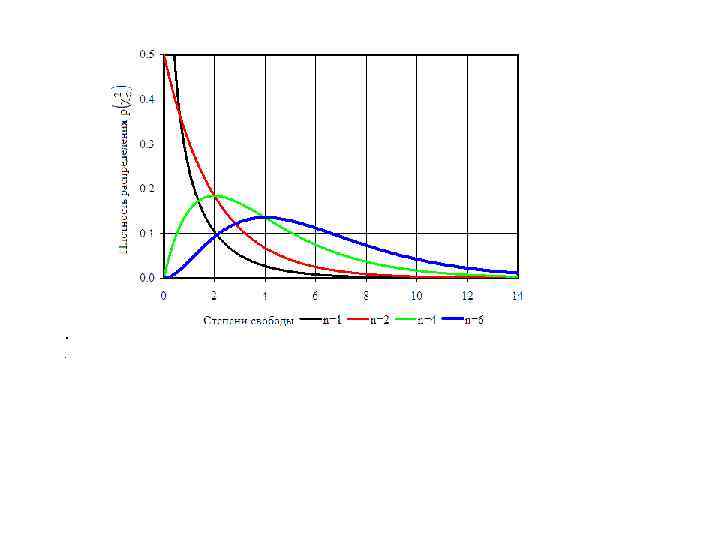2. Распределение Стьюдента (t- распределение). Пусть имеет распределение Стьюдента с к степенями свободы

Сходимость последовательности с. в. по вероятности. Опр. Последовательность с. в. Х 1, Х 2, …, Хn , … сходится по вероятности к числу , если для любого ε>0